(核心素养应用意识)第一单元观察物体(三)(解决问题)测试卷(含解析)-2024-2025学年五年级数学下册人教版
文档属性
| 名称 | (核心素养应用意识)第一单元观察物体(三)(解决问题)测试卷(含解析)-2024-2025学年五年级数学下册人教版 |  | |
| 格式 | doc | ||
| 文件大小 | 474.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 05:45:37 | ||
图片预览


文档简介
/ 让教学更有效 精品试卷 | 数学学科
(核心素养应用意识)第一单元观察物体(三)(解决问题)-2024-2025学年五年级数学下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.根据从前面、上面看到的图形(如图所示),在图上用数字标出从上面看到图形各位置所用的小正方体个数。(写出全部可能的情况)www-2-1-cnjy-com
2.用棱长是1cm的小正方体靠墙角摆成如图所示的几何体。
(1)摆这个几何体一共用了多少个小正方体?
(2)从图中取走( )号小正方体后,从正面、上面、右面看到的图形不变。
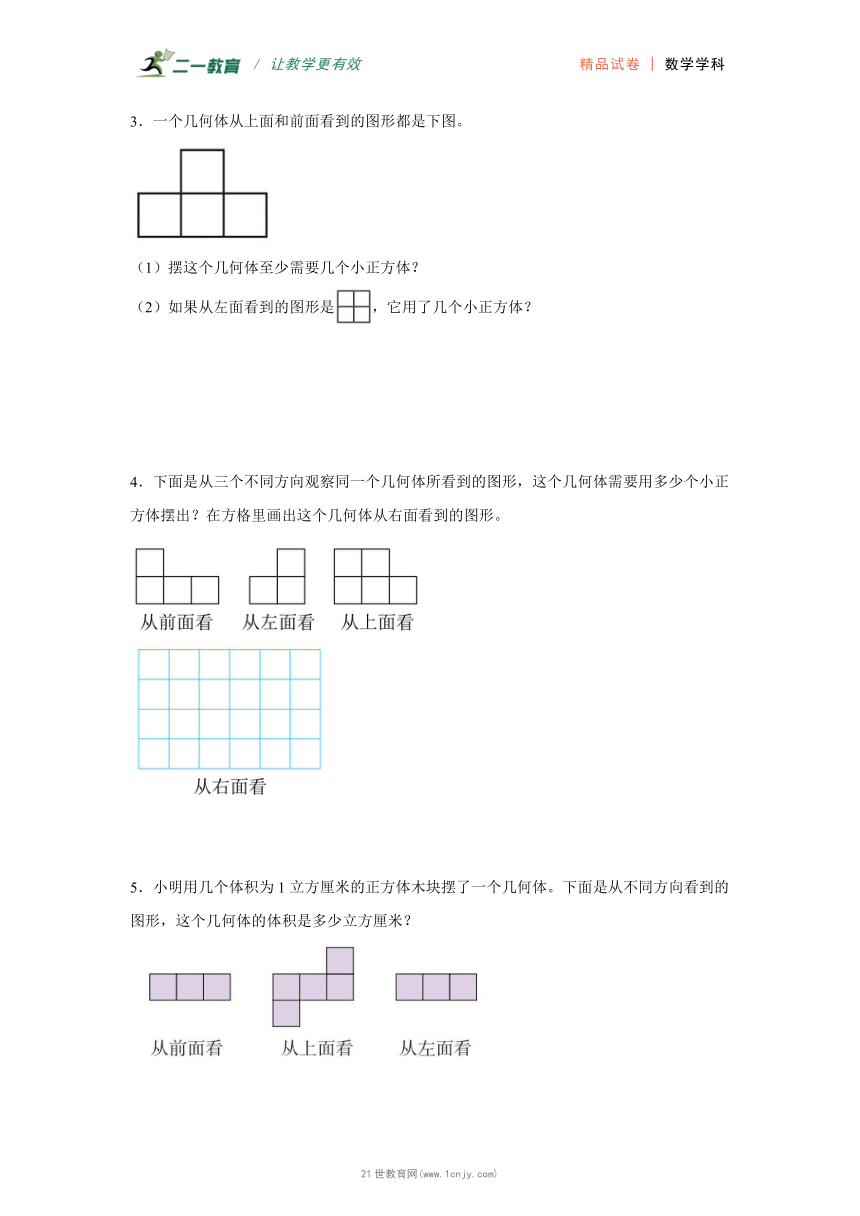
3.一个几何体从上面和前面看到的图形都是下图。
(1)摆这个几何体至少需要几个小正方体?
(2)如果从左面看到的图形是,它用了几个小正方体?
4.下面是从三个不同方向观察同一个几何体所看到的图形,这个几何体需要用多少个小正方体摆出?在方格里画出这个几何体从右面看到的图形。【出处:21教育名师】
5.小明用几个体积为1立方厘米的正方体木块摆了一个几何体。下面是从不同方向看到的图形,这个几何体的体积是多少立方厘米?2-1-c-n-j-y
6.下面是用同样的小正方体摆出的一些几何体。
(1)哪些从前面看是?哪些从左面看是?
(2)从前面观察一个几何体,看到的图形和从前面观察⑤所看到的一样。这个几何体是用5个小正方体摆成的,它有多少种不同的摆法?
(3)同桌之间互相提一个问题并解答。
7.已知一个几何体是由若干个形状和大小完全相同的小立方体组成的,分别从不同的角度所看到的形状如下图。请在草稿纸上画图并结合想象来分析该几何体由几个小立方块组成的?(直接回答结果即可)www.21-cn-jy.com
8.一个立体图形,从上面看到的形状是,从左面看到的形状是,这个立体图形有几种摆法?试画出这几种摆法从正面看到的形状。21世纪教育网版权所有
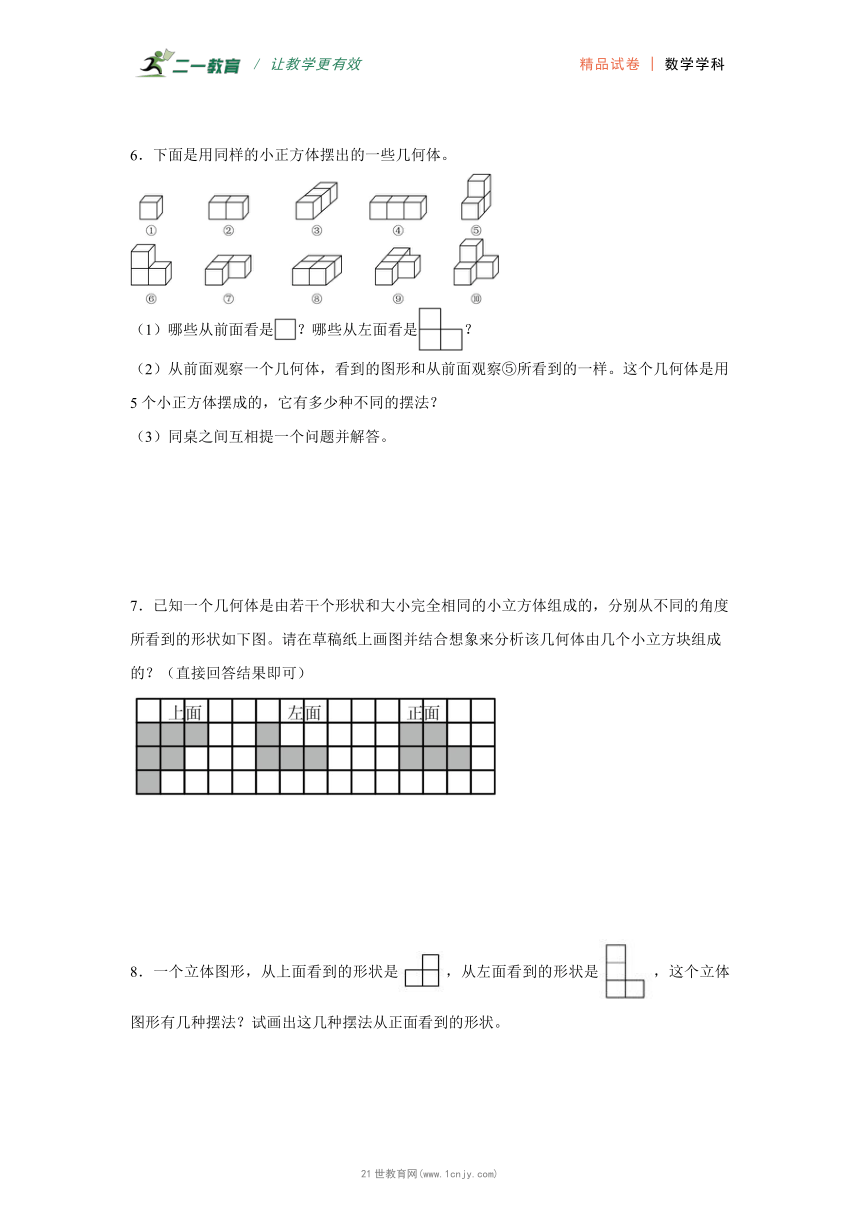
9.(1)画出三角形ABC绕某一顶点旋转90°后的图形。
(2)你画出的图形是把三角形ABC绕点( )( )旋转90°后得到的。
10.按要求答题。
(1)从①号物体和②号物体的( )面、( )面看到的图形相同。
(2)从①号物体和②号物体的( )面看到的图形不同。
(3)画出两个物体从前面看到的图形。
11.如图中的网格是边长为1cm的小正方形。
(1)图2是由图1先向右平移( )格,再绕点A按( )时针方向旋转( )°得到的。
(2)在图1中标出点A。
(3)一个由小正方体搭成的几何体,如果从正面和上面看到的都是图1的形状,那么这个几何体的表面积最少是( )cm2。【来源:21·世纪·教育·网】
12.将几个大小相同的正方体木块放成一堆,图1至图3分别对应该图形从上面、正面、左面看到的图形,则这堆木块共有多少块?21*cnjy*com
13.一个立体图形从上面看的形状是,这个立体图形最下面一层摆了几个小正方体?如果这个立方体图形一共摆两层,最少有几个小正方体?最多可以摆几个小正方体?画出最多、最少两种情况的立体图形?
14.利用大小相等的正方体纸箱若干个,按要求完成纸箱拼搭任务。甜甜要摆的几何体从三个不同方向看到的图形如下:
(1)组成这个几何体,需要( )个纸箱,在“从上面看”的图形上标出对应位置的纸箱个数。
(2)纸箱总数不变,移动一个纸箱,使得从上面看到的图形不变,一共有多少种移法?
(3)若在保持总数不变的情况下,移动一个纸箱使得从前面和上面看到的图形均和从左面看到的一样,可以怎样调整纸箱的位置?
15.下面图形是由若干个小正方体木块搭成的几何体从三个方向观察所看到的图形,请你用小正方体摆一摆该几何体的实际形状,它由多少个小正方体木块搭成?
16.曲米在桌子上摆了一个由若干个同样的小正方体组成的几何体,从上面看到的图形是,从左面看到的图形是。曲米摆出的这个几何体最少需要几个小正方体?最多需要几个小正方体?21cnjy.com
17.请看以下相关信息,解决数学问题。
一个仓库里堆积着若干正方体货箱,这些箱子搬运比较困难,可是仓库管理员要清点一下箱子的数量,于是他将从正面、左面、上面看这堆货物,得到如下的平面图形,你能根据这幅图帮助他清点箱子的数量吗?你是怎么清点的,请把你的想法写下来。
《(核心素养应用意识)第二单元观察物体(三)(解决问题)-2024-2025学年五年级数学下册人教版》参考答案
1.图见详解
【分析】
各位置标记为,综合考虑从前面和上面看到的图形,②号位置上有2个小正方体,③号和⑤号位置上各有1个小正方体,①号位置和④号位置上至少有1个位置上是2个小正方体,据此解答。
【详解】如图:
2.(1)20个
(2)5
【分析】从下往上一层一层数,然后加起来即可;第一层:10个,第二层:1+2+3=6(个),第三层:1+2=3(个),第四层:1个,一共10+6+3+1=10(个),据此解答;
(2)从图中取走1个小正方体后,从正面、上面、右面看到的图形不变,那么这个小正方体必须有3面,即后面、下面、左面都与其他正方体接触,这样拿走它从正面、上面、右面看到的图形不变,所以这个小正方体是5号。21·cn·jy·com
【详解】由分析可知:
(1)10+(1+2+3)+(1+2)+1
=10+6+3+1
=16+3+1
=20(个)
答:这个几何体一共有20个小正方体。
(2)从图中取走5号小正方体后,从正面、上面、右面看到的图形不变。
3.(1)5个
(2)6个
【分析】(1)根据从上面和前面看到的图形,可知这个几何体有两层两行,下层有4个小正方体,上层至少有1个小正方体,一共有(4+1)个小正方体。21·世纪*教育网
(2)根据从左面看到的图形,可知这个几何体有两层两行,下层有4个小正方体,上层至少有2个小正方体,一共有(4+2)个小正方体。21教育名师原创作品
【详解】(1)结合从上面和前面看到的图形,可以得出下面的几何体:
(摆法不唯一)
4+1=5(个)
答:摆这个几何体至少需要5个小正方体。
(2)结合从左面看到的图形,可以得出下面的几何体:
4+2=6(个)
答:它用了6个小正方体。
4.6个;见详解
【分析】根据从三个不同方向观察同一个几何体所看到的图形可知,这个几何体有两层,底层有5个小正方体,上层有1个小正方体且在第一行居左,据此得出摆出这个几何体需要(5+1)个小正方体。
从右面能看到两层3个小正方形,下层2个,上层1个且居左,据此画出从右面看到的图形。
【详解】结合从前面、左面、上面看到的平面图,可以得出下面的几何体:
答:这个几何体需要用6个小正方体摆出。
5.5立方厘米
【分析】根据从不同方向看到的图形,展开想象,小正方体如下图摆放。据此解答。
【详解】1+3+1=5(个)
5×1=5(立方厘米)
答:这个几何体的体积是5立方厘米。
6.(1)①③;⑤⑩
(2)有7种摆法。
(3)哪些从左边看是?①②④(答案不唯一)
【分析】
(1)根据观察几何体可知,①③从前面看是,⑤⑩从左面看是。
(2)观察⑤可以看出,从前面看是由两个正方形竖着叠起来的,用5个小正方体来摆,只要把5个小正方体摆成一列两行即可,所以有7种摆法。21教育网
(3)哪些从左边看是?
【详解】
(1)①③从前面看是,⑤⑩从左面看是。
(2)根据对图形的观察,结合空间想象能力可知有7种摆法。
(3)哪些从左边看是?①②④(答案不唯一)
7.8个
【分析】由从上面看到的图形可知,这个几何体的第一层有6个小立方块;由左面和正面看到的图形可知,这个几何体的第二层有2个小立方块,则该几何体有6+2=8个小立方块。
【详解】如图所示:
6+2=8(个)
答:该几何体由8个小立方块组成的。
【点睛】本题考查通过三视图确认几何体,明确从三个方向观察到的形状是解题的关键。
8.一种;图形见详解
【分析】
由题意可知,从上面看到的形状是,则该立体图形有两列,第一列有1个正方体,第二列有2个正方体;从左面看到的形状是,则该立体图形有两层,第一层有2个正方体,第二层和第三层都有1个正方体;据此可知这个立体图形的摆法,从正面观察,可以看到三层,最下面一层2个正方形,上面两层各一个正方形居右,据此作图。
【详解】由分析可知:
这个立体图形有一种摆法。摆法如下:
则个立体图形有一种摆法,从正面看到的形状是:。
【点睛】本题考查通过三视图确定几何体,明确从不同方向观察到的形状是解题的关键。
9.(1)见详解
(2)B;逆时针
【分析】(1)选择B点不动,根据旋转的特征,将三角形ABC绕B点逆时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的三角形A'BC'。2·1·c·n·j·y
(2)根据旋转的三要素:旋转中心、旋转方向、旋转角度解答。
【详解】(1)三角形ABC绕B点逆时针旋转90°后得到旋转后的三角形,如图。(答案不唯一)
(2)画出的图形是把三角形ABC绕点B逆时针旋转90°后得到的。
【点睛】掌握作旋转后的图形的作图方法是解题的关键。
10.(1)上;侧(2)前、后(3)见详解
【分析】(1)分别从不同方向观察两个图形可知,从①号物体和②号物体的上面看到的都是,从左侧面和右侧面看到的图形都是。【来源:21cnj*y.co*m】
(2)通过观察可知,从两个图形的前面和后面看到的图形不同。
(3)①号物体从前面看有2层:下层3个小正方形,上层1个小正方形居左;②号物体从前面看有2层:下层3个小正方形,上层1个小正方形居中。据此画图。
【详解】(1)从①号物体和②号物体的上面、侧面看到的图形相同。
(2)从①号物体和②号物体的前、后面看到的图形不同。
(3)
【点睛】本题考查物体三视图的认识和画法。需要运用空间想象力解决此类问题。
11.(1)6;逆;90
(2)见详解
(3)22
【分析】(1)平移是指在平面内,将一个图形沿着某个方向移动一定的距离,称为平移;旋转是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。【版权所有:21教育】
(2)旋转中心是不动的,据此找到点A的位置。
(3)从正面和上面看到的都是图1的形状,那么这个几何体至少用了5个正方体拼成,如图:,这个几何体的上下面各有4个小正方形,左右面各有3个小正方形,前后面各有4个小正方形;先计算出正方形的总个数,再乘每个正方形的面积,就是几何体最少的表面积。
【详解】(1)先确定旋转中心A点,将图1向右平移6格,图1点A与图2点A重合,再将图1绕点逆时针旋转90°可得到图2;
(2)在图1中标出点A,作图如下:
(3)拼成的几何体是。
(4+3+4)×2
=11×2
=22(个)
1×1×22=22(cm2)
【点睛】掌握图形的平移、旋转的特点,以及能根据部分视图还原立体图形是解题的关键。
12.9块
【分析】由从上向下看到的视图易得最底层小正方体的个数,由从正面看到的视图和从左向右看到的视图找到其余层数里小正方体的个数相加即可。
【详解】如图:
由从上向下看到的视图易得最底层有6个小正方体,第二层最多也有2个小正方体,第二层最多也有1个小正方体,
所以这堆木块最多共有
6+2+1
=8+1
=9(块)
答:这堆木块共有9块。
【点睛】考查了从不同方向观察物体和几何体,解答此题应注意从上向下看到的视图决定底层正方体的个数。
13.4;5;8;图形见详解
【分析】从上面观察立体图形的平面图可以确定每个位置上的小正方体,根据这个平面图形摆立体图形最下面一层摆了4个小正方体;如果这个立方体图形一共摆两层,小正方体的数量最少,那么第二层最少有1个小正方体,小正方体的个数为(4+1)个;如果这个立方体图形一共摆两层,小正方体的数量最多,那么第二层最多有4个小正方体,小正方体的个数为(4+4)个;据此解答。
【详解】(1)如图所示,这个立体图形最下面一层摆了4个小正方体;
(2)如图所示,如果这个立方体图形一共摆两层,最少有5个小正方体;
(3)如图所示,如果这个立方体图形一共摆两层,最多可以摆8个小正方体。
【点睛】掌握根据平面图形确定立体图形小正方体个数的方法是解答题目的关键。
14.(1)10;图见详解
(2)12种
(3)见详解
【分析】
(1)根据如下可知,这个几何体有3层;从上面看到图形可知,这个几何体最下层需要7个小正方体纸箱;从前面和左面看到图形可知,这个几何体的中间层需要2个小正方体纸箱,最上层需要1个小正方体纸箱,一共需要(7+2+1)个小正方体纸箱。再用数字标出在“从上面看”的图形上标出对应位置如图:。
(2)可以把最上层的正方形纸箱也就是③放入其它6个位置的任何一个位置,则从上面看到的图形不变,或把从中间层左边的小正方体纸箱也就是②放到其它6个位置的任何一个位置,则从上面看到的图形不变;共有(6+6)种方法,据此解答。
(3)把从前面看到图形的最下层最左边的小正方形(也就是从上面看到最左边的小正方形)也就是①移到从前面看的中间层的右边与中间层的小正方体挨着也就是与中间层①的位置,看到的图形和从左面看到的图形相同;据此解答。
【详解】(1)7+2+1
=9+1
=10(个)
如图:
(2)6+6=12(种)
答:一共有12种移法。
(3)如图:
根据分析可知,把最上层左边①移到中间层①的位置,从前面和上面看到的图形均和从左面看到的一样。
15.6个
【分析】主视图、左视图可以判定有三列,两行,俯视图判定第一层有4个正方体,第二层有2个正方体,由此得出答案即可。21*cnjy*com
【详解】第一层有4个正方体,第二层有2个正方体;
4+2=6(个)
答:由6个小正方体木块搭成。
【点睛】本题考查了观察物体的知识点,可以借助物体摆一摆。
16.最少需要5个小正方体;最多需要7个小正方体
【分析】根据图形从上看和从左看可知,这个图形有2列,前面一行只有1层,只有1个正方体,后面是2层,最多可放6个正方体,最少可放4个正方体,最多就是1+6=7个;最少就是1+4=5个,即可解答。
【详解】根据题意可知:最少需要:4+1=5(个)
最多需要:6+1=7(个)
答:曲米摆出的这个几何体最少需要5个正方体;最多需要7个正方体。
【点睛】本题考查从不同方向观察物体和几何体,根据从不同的位置看到的图形解答问题。
17.11个;具体想法见详解
【分析】
根据从上面和从左面看到的图形可以知道第一排有1层,中间一排有3层,第三排有2层且中间那一排的中间没有货物;再根据从前面看到的图形知道中间那一排的左侧和右侧有3层,第三排的中间有1层,即(图形上的数字表示从上面看时,这个位置上箱子的个数),把从上面看到的图形上的数字相加即为箱子的总数量,据此解答。
【详解】根据从上面和左面看到的图形可以确定第一排,第二排,第三排的箱子层数分别是:1层,3层和2层并且第二排的中间是没有箱子的;再根据从前面和左边看到的图形可以知道第二排的左侧和右侧各有3层,第三排的中间只有1个箱子,左侧有2个箱子,因此从上面看时每个位置上箱子的个数如下:
把图形上的数字相加即为箱子的总数量:2+1+3+3+1+1=11(个)
答:一共有11个箱子。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
(核心素养应用意识)第一单元观察物体(三)(解决问题)-2024-2025学年五年级数学下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.根据从前面、上面看到的图形(如图所示),在图上用数字标出从上面看到图形各位置所用的小正方体个数。(写出全部可能的情况)www-2-1-cnjy-com
2.用棱长是1cm的小正方体靠墙角摆成如图所示的几何体。
(1)摆这个几何体一共用了多少个小正方体?
(2)从图中取走( )号小正方体后,从正面、上面、右面看到的图形不变。
3.一个几何体从上面和前面看到的图形都是下图。
(1)摆这个几何体至少需要几个小正方体?
(2)如果从左面看到的图形是,它用了几个小正方体?
4.下面是从三个不同方向观察同一个几何体所看到的图形,这个几何体需要用多少个小正方体摆出?在方格里画出这个几何体从右面看到的图形。【出处:21教育名师】
5.小明用几个体积为1立方厘米的正方体木块摆了一个几何体。下面是从不同方向看到的图形,这个几何体的体积是多少立方厘米?2-1-c-n-j-y
6.下面是用同样的小正方体摆出的一些几何体。
(1)哪些从前面看是?哪些从左面看是?
(2)从前面观察一个几何体,看到的图形和从前面观察⑤所看到的一样。这个几何体是用5个小正方体摆成的,它有多少种不同的摆法?
(3)同桌之间互相提一个问题并解答。
7.已知一个几何体是由若干个形状和大小完全相同的小立方体组成的,分别从不同的角度所看到的形状如下图。请在草稿纸上画图并结合想象来分析该几何体由几个小立方块组成的?(直接回答结果即可)www.21-cn-jy.com
8.一个立体图形,从上面看到的形状是,从左面看到的形状是,这个立体图形有几种摆法?试画出这几种摆法从正面看到的形状。21世纪教育网版权所有
9.(1)画出三角形ABC绕某一顶点旋转90°后的图形。
(2)你画出的图形是把三角形ABC绕点( )( )旋转90°后得到的。
10.按要求答题。
(1)从①号物体和②号物体的( )面、( )面看到的图形相同。
(2)从①号物体和②号物体的( )面看到的图形不同。
(3)画出两个物体从前面看到的图形。
11.如图中的网格是边长为1cm的小正方形。
(1)图2是由图1先向右平移( )格,再绕点A按( )时针方向旋转( )°得到的。
(2)在图1中标出点A。
(3)一个由小正方体搭成的几何体,如果从正面和上面看到的都是图1的形状,那么这个几何体的表面积最少是( )cm2。【来源:21·世纪·教育·网】
12.将几个大小相同的正方体木块放成一堆,图1至图3分别对应该图形从上面、正面、左面看到的图形,则这堆木块共有多少块?21*cnjy*com
13.一个立体图形从上面看的形状是,这个立体图形最下面一层摆了几个小正方体?如果这个立方体图形一共摆两层,最少有几个小正方体?最多可以摆几个小正方体?画出最多、最少两种情况的立体图形?
14.利用大小相等的正方体纸箱若干个,按要求完成纸箱拼搭任务。甜甜要摆的几何体从三个不同方向看到的图形如下:
(1)组成这个几何体,需要( )个纸箱,在“从上面看”的图形上标出对应位置的纸箱个数。
(2)纸箱总数不变,移动一个纸箱,使得从上面看到的图形不变,一共有多少种移法?
(3)若在保持总数不变的情况下,移动一个纸箱使得从前面和上面看到的图形均和从左面看到的一样,可以怎样调整纸箱的位置?
15.下面图形是由若干个小正方体木块搭成的几何体从三个方向观察所看到的图形,请你用小正方体摆一摆该几何体的实际形状,它由多少个小正方体木块搭成?
16.曲米在桌子上摆了一个由若干个同样的小正方体组成的几何体,从上面看到的图形是,从左面看到的图形是。曲米摆出的这个几何体最少需要几个小正方体?最多需要几个小正方体?21cnjy.com
17.请看以下相关信息,解决数学问题。
一个仓库里堆积着若干正方体货箱,这些箱子搬运比较困难,可是仓库管理员要清点一下箱子的数量,于是他将从正面、左面、上面看这堆货物,得到如下的平面图形,你能根据这幅图帮助他清点箱子的数量吗?你是怎么清点的,请把你的想法写下来。
《(核心素养应用意识)第二单元观察物体(三)(解决问题)-2024-2025学年五年级数学下册人教版》参考答案
1.图见详解
【分析】
各位置标记为,综合考虑从前面和上面看到的图形,②号位置上有2个小正方体,③号和⑤号位置上各有1个小正方体,①号位置和④号位置上至少有1个位置上是2个小正方体,据此解答。
【详解】如图:
2.(1)20个
(2)5
【分析】从下往上一层一层数,然后加起来即可;第一层:10个,第二层:1+2+3=6(个),第三层:1+2=3(个),第四层:1个,一共10+6+3+1=10(个),据此解答;
(2)从图中取走1个小正方体后,从正面、上面、右面看到的图形不变,那么这个小正方体必须有3面,即后面、下面、左面都与其他正方体接触,这样拿走它从正面、上面、右面看到的图形不变,所以这个小正方体是5号。21·cn·jy·com
【详解】由分析可知:
(1)10+(1+2+3)+(1+2)+1
=10+6+3+1
=16+3+1
=20(个)
答:这个几何体一共有20个小正方体。
(2)从图中取走5号小正方体后,从正面、上面、右面看到的图形不变。
3.(1)5个
(2)6个
【分析】(1)根据从上面和前面看到的图形,可知这个几何体有两层两行,下层有4个小正方体,上层至少有1个小正方体,一共有(4+1)个小正方体。21·世纪*教育网
(2)根据从左面看到的图形,可知这个几何体有两层两行,下层有4个小正方体,上层至少有2个小正方体,一共有(4+2)个小正方体。21教育名师原创作品
【详解】(1)结合从上面和前面看到的图形,可以得出下面的几何体:
(摆法不唯一)
4+1=5(个)
答:摆这个几何体至少需要5个小正方体。
(2)结合从左面看到的图形,可以得出下面的几何体:
4+2=6(个)
答:它用了6个小正方体。
4.6个;见详解
【分析】根据从三个不同方向观察同一个几何体所看到的图形可知,这个几何体有两层,底层有5个小正方体,上层有1个小正方体且在第一行居左,据此得出摆出这个几何体需要(5+1)个小正方体。
从右面能看到两层3个小正方形,下层2个,上层1个且居左,据此画出从右面看到的图形。
【详解】结合从前面、左面、上面看到的平面图,可以得出下面的几何体:
答:这个几何体需要用6个小正方体摆出。
5.5立方厘米
【分析】根据从不同方向看到的图形,展开想象,小正方体如下图摆放。据此解答。
【详解】1+3+1=5(个)
5×1=5(立方厘米)
答:这个几何体的体积是5立方厘米。
6.(1)①③;⑤⑩
(2)有7种摆法。
(3)哪些从左边看是?①②④(答案不唯一)
【分析】
(1)根据观察几何体可知,①③从前面看是,⑤⑩从左面看是。
(2)观察⑤可以看出,从前面看是由两个正方形竖着叠起来的,用5个小正方体来摆,只要把5个小正方体摆成一列两行即可,所以有7种摆法。21教育网
(3)哪些从左边看是?
【详解】
(1)①③从前面看是,⑤⑩从左面看是。
(2)根据对图形的观察,结合空间想象能力可知有7种摆法。
(3)哪些从左边看是?①②④(答案不唯一)
7.8个
【分析】由从上面看到的图形可知,这个几何体的第一层有6个小立方块;由左面和正面看到的图形可知,这个几何体的第二层有2个小立方块,则该几何体有6+2=8个小立方块。
【详解】如图所示:
6+2=8(个)
答:该几何体由8个小立方块组成的。
【点睛】本题考查通过三视图确认几何体,明确从三个方向观察到的形状是解题的关键。
8.一种;图形见详解
【分析】
由题意可知,从上面看到的形状是,则该立体图形有两列,第一列有1个正方体,第二列有2个正方体;从左面看到的形状是,则该立体图形有两层,第一层有2个正方体,第二层和第三层都有1个正方体;据此可知这个立体图形的摆法,从正面观察,可以看到三层,最下面一层2个正方形,上面两层各一个正方形居右,据此作图。
【详解】由分析可知:
这个立体图形有一种摆法。摆法如下:
则个立体图形有一种摆法,从正面看到的形状是:。
【点睛】本题考查通过三视图确定几何体,明确从不同方向观察到的形状是解题的关键。
9.(1)见详解
(2)B;逆时针
【分析】(1)选择B点不动,根据旋转的特征,将三角形ABC绕B点逆时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的三角形A'BC'。2·1·c·n·j·y
(2)根据旋转的三要素:旋转中心、旋转方向、旋转角度解答。
【详解】(1)三角形ABC绕B点逆时针旋转90°后得到旋转后的三角形,如图。(答案不唯一)
(2)画出的图形是把三角形ABC绕点B逆时针旋转90°后得到的。
【点睛】掌握作旋转后的图形的作图方法是解题的关键。
10.(1)上;侧(2)前、后(3)见详解
【分析】(1)分别从不同方向观察两个图形可知,从①号物体和②号物体的上面看到的都是,从左侧面和右侧面看到的图形都是。【来源:21cnj*y.co*m】
(2)通过观察可知,从两个图形的前面和后面看到的图形不同。
(3)①号物体从前面看有2层:下层3个小正方形,上层1个小正方形居左;②号物体从前面看有2层:下层3个小正方形,上层1个小正方形居中。据此画图。
【详解】(1)从①号物体和②号物体的上面、侧面看到的图形相同。
(2)从①号物体和②号物体的前、后面看到的图形不同。
(3)
【点睛】本题考查物体三视图的认识和画法。需要运用空间想象力解决此类问题。
11.(1)6;逆;90
(2)见详解
(3)22
【分析】(1)平移是指在平面内,将一个图形沿着某个方向移动一定的距离,称为平移;旋转是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。【版权所有:21教育】
(2)旋转中心是不动的,据此找到点A的位置。
(3)从正面和上面看到的都是图1的形状,那么这个几何体至少用了5个正方体拼成,如图:,这个几何体的上下面各有4个小正方形,左右面各有3个小正方形,前后面各有4个小正方形;先计算出正方形的总个数,再乘每个正方形的面积,就是几何体最少的表面积。
【详解】(1)先确定旋转中心A点,将图1向右平移6格,图1点A与图2点A重合,再将图1绕点逆时针旋转90°可得到图2;
(2)在图1中标出点A,作图如下:
(3)拼成的几何体是。
(4+3+4)×2
=11×2
=22(个)
1×1×22=22(cm2)
【点睛】掌握图形的平移、旋转的特点,以及能根据部分视图还原立体图形是解题的关键。
12.9块
【分析】由从上向下看到的视图易得最底层小正方体的个数,由从正面看到的视图和从左向右看到的视图找到其余层数里小正方体的个数相加即可。
【详解】如图:
由从上向下看到的视图易得最底层有6个小正方体,第二层最多也有2个小正方体,第二层最多也有1个小正方体,
所以这堆木块最多共有
6+2+1
=8+1
=9(块)
答:这堆木块共有9块。
【点睛】考查了从不同方向观察物体和几何体,解答此题应注意从上向下看到的视图决定底层正方体的个数。
13.4;5;8;图形见详解
【分析】从上面观察立体图形的平面图可以确定每个位置上的小正方体,根据这个平面图形摆立体图形最下面一层摆了4个小正方体;如果这个立方体图形一共摆两层,小正方体的数量最少,那么第二层最少有1个小正方体,小正方体的个数为(4+1)个;如果这个立方体图形一共摆两层,小正方体的数量最多,那么第二层最多有4个小正方体,小正方体的个数为(4+4)个;据此解答。
【详解】(1)如图所示,这个立体图形最下面一层摆了4个小正方体;
(2)如图所示,如果这个立方体图形一共摆两层,最少有5个小正方体;
(3)如图所示,如果这个立方体图形一共摆两层,最多可以摆8个小正方体。
【点睛】掌握根据平面图形确定立体图形小正方体个数的方法是解答题目的关键。
14.(1)10;图见详解
(2)12种
(3)见详解
【分析】
(1)根据如下可知,这个几何体有3层;从上面看到图形可知,这个几何体最下层需要7个小正方体纸箱;从前面和左面看到图形可知,这个几何体的中间层需要2个小正方体纸箱,最上层需要1个小正方体纸箱,一共需要(7+2+1)个小正方体纸箱。再用数字标出在“从上面看”的图形上标出对应位置如图:。
(2)可以把最上层的正方形纸箱也就是③放入其它6个位置的任何一个位置,则从上面看到的图形不变,或把从中间层左边的小正方体纸箱也就是②放到其它6个位置的任何一个位置,则从上面看到的图形不变;共有(6+6)种方法,据此解答。
(3)把从前面看到图形的最下层最左边的小正方形(也就是从上面看到最左边的小正方形)也就是①移到从前面看的中间层的右边与中间层的小正方体挨着也就是与中间层①的位置,看到的图形和从左面看到的图形相同;据此解答。
【详解】(1)7+2+1
=9+1
=10(个)
如图:
(2)6+6=12(种)
答:一共有12种移法。
(3)如图:
根据分析可知,把最上层左边①移到中间层①的位置,从前面和上面看到的图形均和从左面看到的一样。
15.6个
【分析】主视图、左视图可以判定有三列,两行,俯视图判定第一层有4个正方体,第二层有2个正方体,由此得出答案即可。21*cnjy*com
【详解】第一层有4个正方体,第二层有2个正方体;
4+2=6(个)
答:由6个小正方体木块搭成。
【点睛】本题考查了观察物体的知识点,可以借助物体摆一摆。
16.最少需要5个小正方体;最多需要7个小正方体
【分析】根据图形从上看和从左看可知,这个图形有2列,前面一行只有1层,只有1个正方体,后面是2层,最多可放6个正方体,最少可放4个正方体,最多就是1+6=7个;最少就是1+4=5个,即可解答。
【详解】根据题意可知:最少需要:4+1=5(个)
最多需要:6+1=7(个)
答:曲米摆出的这个几何体最少需要5个正方体;最多需要7个正方体。
【点睛】本题考查从不同方向观察物体和几何体,根据从不同的位置看到的图形解答问题。
17.11个;具体想法见详解
【分析】
根据从上面和从左面看到的图形可以知道第一排有1层,中间一排有3层,第三排有2层且中间那一排的中间没有货物;再根据从前面看到的图形知道中间那一排的左侧和右侧有3层,第三排的中间有1层,即(图形上的数字表示从上面看时,这个位置上箱子的个数),把从上面看到的图形上的数字相加即为箱子的总数量,据此解答。
【详解】根据从上面和左面看到的图形可以确定第一排,第二排,第三排的箱子层数分别是:1层,3层和2层并且第二排的中间是没有箱子的;再根据从前面和左边看到的图形可以知道第二排的左侧和右侧各有3层,第三排的中间只有1个箱子,左侧有2个箱子,因此从上面看时每个位置上箱子的个数如下:
把图形上的数字相加即为箱子的总数量:2+1+3+3+1+1=11(个)
答:一共有11个箱子。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
