(核心素养运用能力)第三单元长方体和正方体(表面积切拼 组合体计算)测试卷(含解析)-2024-2025学年人教版五年级数学下册
文档属性
| 名称 | (核心素养运用能力)第三单元长方体和正方体(表面积切拼 组合体计算)测试卷(含解析)-2024-2025学年人教版五年级数学下册 |  | |
| 格式 | doc | ||
| 文件大小 | 375.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 05:49:26 | ||
图片预览


文档简介
/ 让教学更有效 精品试卷 | 数学学科
(核心素养运用能力)第三单元长方体和正方体(表面积切拼 组合体计算)-2024-2025学年五年级数学下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、计算题
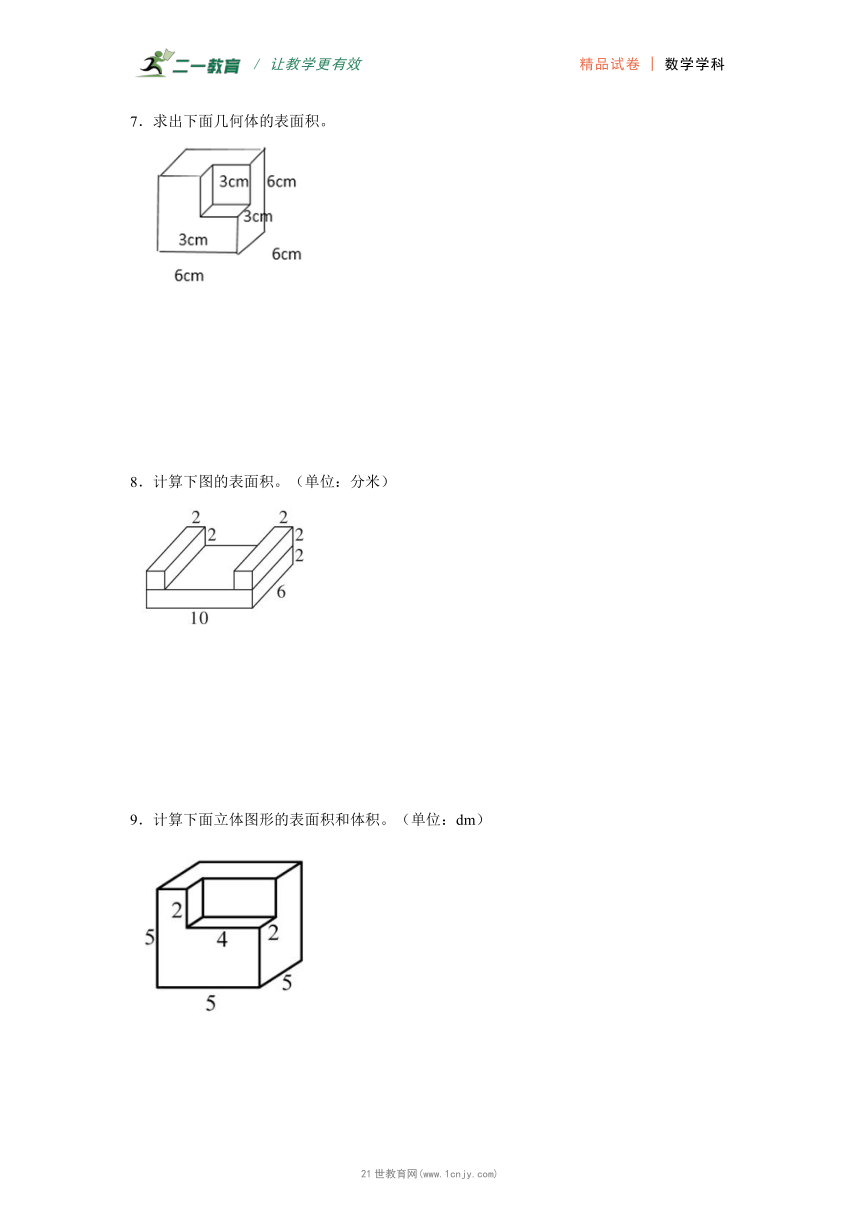
1.计算下图的表面积。(单位:分米)
2.计算下面图形的表面积。(单位:dm)
3.计算下面图形的表面积。(单位:cm)
4.计算如图图形的表面积。(单位:cm)
5.计算下面图形的表面积。
(1)
(2)
6.计算下面图形的表面积。
(1) (2)
7.求出下面几何体的表面积。
8.计算下图的表面积。(单位:分米)
9.计算下面立体图形的表面积和体积。(单位:dm)
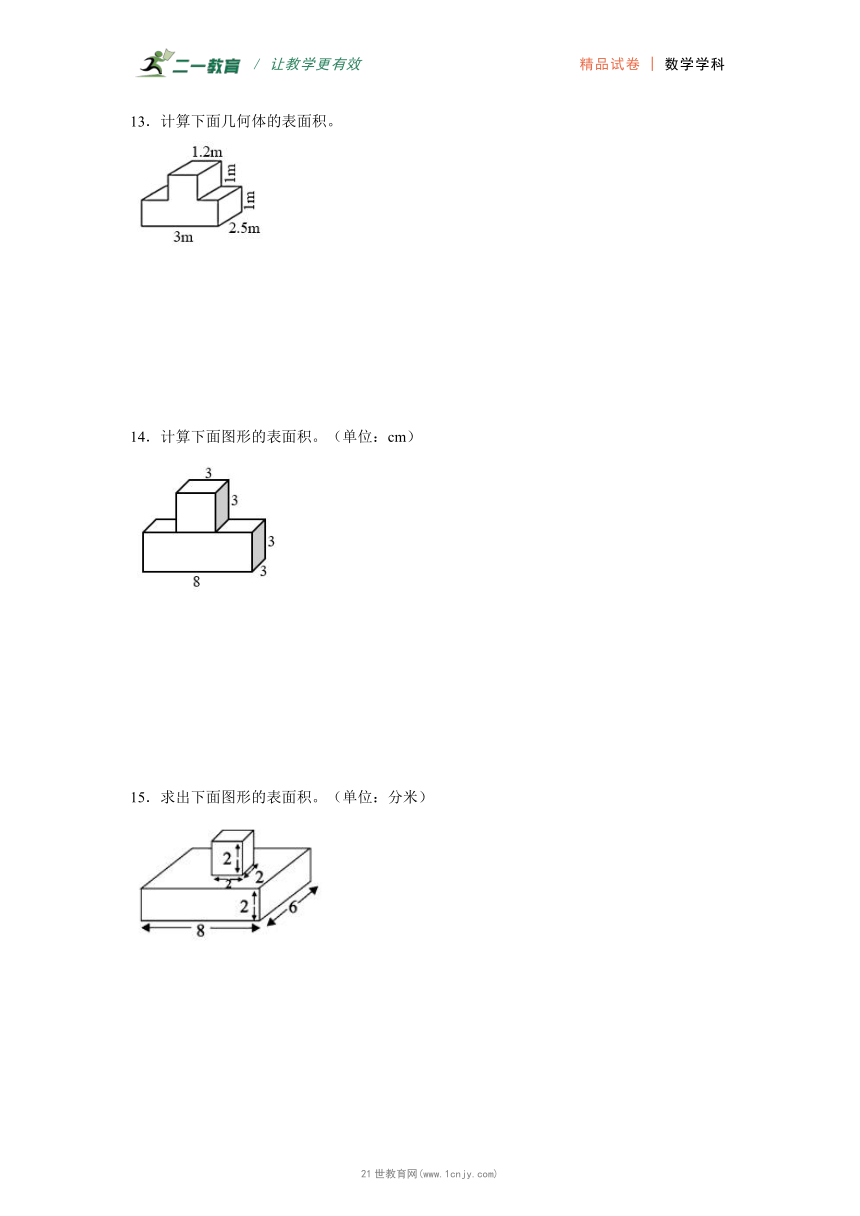
10.计算这个零件的表面积。(单位:厘米)
11.计算组合图形的表面积。
12.从一个正方体木块中间挖去一个长3dm、宽2dm、高2dm的长方体木块,求剩下木块的表面积。
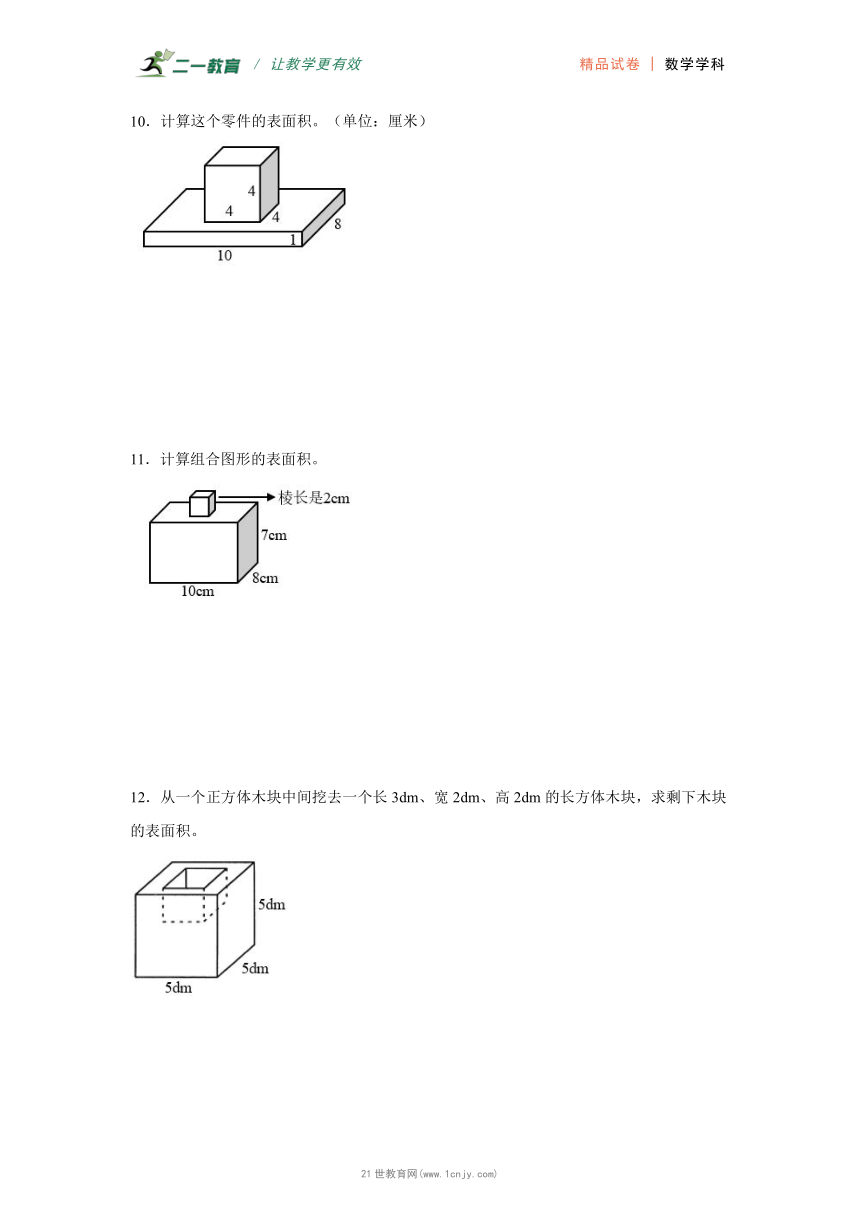
13.计算下面几何体的表面积。
14.计算下面图形的表面积。(单位:cm)
15.求出下面图形的表面积。(单位:分米)
16.求下面图形的表面积。
17.计算下面组合图形的表面积。
18.求出下列图形的表面积。
19.求下面组合图形的表面积。(单位:厘米)
20.计算下面组合图形的表面积。(单位:cm)
21.计算下面图形的表面积,单位(cm)。
22.有一个形状如下的零件,求它的表面积。(单位:cm)
23.计算下面图形的表面积。(单位:dm)
《(核心素养运用能力)第三单元长方体和正方体(表面积切拼 组合体计算)-2024-2025学年五年级数学下册人教版》参考答案21世纪教育网版权所有
1.844平方分米
【分析】根据图示,组合图形的表面积=长方体表面积+正方体表面积,依据长方体表面积公式:长方体表面积=(长×宽+长×高+宽×高)×2,因为正方体有一个面是与长方体相接的,所以只有4个面,所以,可以直接计算4个面的面积。最后将得出的结果相加即可。
【详解】长方形的表面积:
(15×10+15×8+10×8)×2
=(150+120+80)×2
=350×2
=700(平方分米)
正方体的表面积:
6×6×4
=36×4
=144(平方分米)
700+144=844(平方分米)
图形的表面积为844平方分米。
2.1020dm2
【分析】图形的表面积等于长是20dm、宽是6dm、高是15dm的长方体的表面积加上长是6dm、宽是20-7×2=6(dm)的两个正方形的面积,再减去边长为6dm的两个正方形的面积;所以图形的表面积就是长是20dm、宽是6dm、高是15dm的长方体的表面积;根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】20-7×2
=20-14
=6(dm)
(20×6+20×15+15×6)×2
=(120+300+90)×2
=(420+90)×2
=510×2
=1020(dm2)
3.306cm2
【分析】观察图形可知,组合体的表面积=长10cm,宽7cm,高3cm的长方体的表面积+四个棱长是4cm的正方形的面积。根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,正方形面积公式:面积=边长×边长,代入数据,即可解答。
【详解】(10×7+10×3+7×3)×2+4×4×4
=(70+30+21)×2+16×4
=(100+21)×2+64
=121×2+64
=242+64
=306(cm2)
组合体表面积是306cm2。
4.306cm2
【分析】由于正方体与长方体有重合面,相当于少了2个正方形的面积,所以上面的正方体只求4个侧面的面积,下面的长方体求出表面积,然后相加即可求出组合图形的表面积。
正方体表面积=棱长×棱长×6;长方体表面积=(长×宽+长×高+宽×高)×2。
【详解】4×4×4+(10×7+10×3+7×3)×2
=16×4+(70+30+21)×2
=64+121×2
=64+242
=306(cm2)
它的表面积是306cm2。
5.(1)150cm2
(2)432m2
【分析】(1)根据正方形边长=周长÷4,求出底面边长,可知这是一个正方体,根据正方体表面积=棱长×棱长×6,列式计算即可;21·cn·jy·com
(2)看图可知,在长方体的顶点挖去一个长方体,看上去表面积少了3个面,里面又出现了同样的3个面,因此这个立体图形的表面积就是完整的长方体表面积,根据长方体表面积=(长×宽+长×高+宽×高)×2,列式计算即可。2·1·c·n·j·y
【详解】(1)20÷4=5(cm)
5×5×6=150(cm2)
正方体的表面积是150cm2。
(2)(12×6+12×8+6×8)×2
=(72+96+48)×2
=216×2
=432(m2)
这个立体图形的表面积是432m2。
6.(1)
(2)
【分析】(1)根据长方体的表面积=(长×宽+长×高+宽×高)×2,带入数据计算即可;
(2)长方体上底面少了一个正方形,把上面正方体的上底面移到下底面即可拼成一个完整的长方体的表面积和上面正方体的四个侧面即四个正方形,即用长方体的表面积加上4个正方形的面积即可。21·世纪*教育网
【详解】(1)
(2)
7.216cm2
【分析】观察图形可知,这个几何体虽然切去了一块,但是通过面的平移可得:这个几何体的表面积等于棱长为6cm的正方体的表面积。正方体的表面积=棱长×棱长×6,据此解答。
【详解】6×6×6=216(cm2)
则这个几何体的表面积是216cm2。
8.248平方分米
【分析】表面积是指物体外表面积,通常是指物体表面的总面积。上面的两个小长方形和凹进去的长方形合在一起恰好就是一个长方体的表面积。则表面积=长方体的表面积+4个长方形的面积+4个小正方形的面积。长方体的表面积=(长×宽+长×高+宽×高)×2,小长方形的长是6分米,宽是2分米,面积=长×宽。正方形的边长是2分米,面积=边长×边长。www-2-1-cnjy-com
【详解】
=
=
=(平方分米)
(平方分米)
(平方分米)
(平方分米)
则图形的表面积是248平方分米。
9.150;109
【分析】由图可知:在正方体的顶点处去掉一个小长方体,虽然体积减少了,但是表面积不变。根据正方体的表面积公式:S=6a2,体积公式:V=a3,长方体的体积公式:V=abh,把数据分别代入公式解答即可。【来源:21cnj*y.co*m】
【详解】
=25×6
=150()
=25×5
=125()
=8×2
=16()
V:125-16=109()
故立体图形的表面积是150,体积是109。
【点睛】此题主要考查正方体的表面积公式、体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
10.260平方厘米
【分析】在长10厘米、宽8厘米、高1厘米的长方体放上一个棱长为4厘米的正方体,则表面积比原来长方体多了4个正方形面,每个正方形的边长是4厘米,根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(10×8+10×1+8×1)×2+4×4×4即可求出这个零件的表面积。www.21-cn-jy.com
【详解】(10×8+10×1+8×1)×2+4×4×4
=(80+10+8)×2+4×4×4
=98×2+4×4×4
=196+64
=260(平方厘米)
这个零件的表面积是260平方厘米。
11.428cm2
【分析】观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;21*cnjy*com
组合图形的表面积=长方体的表面积+正方体的4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算即可。
【详解】长方体的表面积:
(10×8+10×7+8×7)×2
=(80+70+56)×2
=206×2
=412(cm2)
正方体4个面的面积:
2×2×4
=4×4
=16(cm2)
一共:412+16=428(cm2)
组合图形的表面积是428cm2。
12.170dm2
【分析】在一个大正方体里,挖去一个长方体,表面积增加了,是原来的正方体表面积再加上小长方体的前后左右4个面。【出处:21教育名师】
【详解】正方体的表面积:5×5×6
=25×6
=150(dm2)
长方体的表面积:(3×2+2×2)×2
=(6+4)×2
=10×2
=20(dm2)
150+20=170(dm2)
剩下木块的表面积是170dm2。
13.33.4m2
【分析】如图:
观察图形可知,两个长方体有重合的部分,把小长方体的上面向下平移,补给大长方体的上面;这样大长方体的表面积是6个面的面积之和,而小长方体只需计算4个面(前后面和左右面)的面积。【版权所有:21教育】
组合图形的表面积=小长方体4个面的面积+大长方体的表面积,小长方体4个面的面积=(长×高+宽×高)×2,大长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。21教育名师原创作品
【详解】(1.2×1+2.5×1)×2+(3×2.5+3×1+2.5×1)×2
=(1.2+2.5)×2+(7.5+3+2.5)×2
=3.7×2+13×2
=7.4+26
=33.4(m2)
几何体的表面积是33.4m2。
14.150cm2
【分析】观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;所以组合图形的表面积=长方体的表面积+正方体的4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算即可。21*cnjy*com
【详解】长方体的表面积:
(8×3+8×3+3×3)×2
=(24+24+9)×2
=57×2
=114(cm2)
正方体4个面的面积:
3×3×4
=9×4
=36(cm2)
一共:114+36=150(cm2)
图形的表面积是150cm2。
15.168平方分米
【分析】观察组合图形可得:组合图形表面积=长方体表面积+正方体的4个面的面积。
【详解】(8×6+8×2+2×6)×2+2×2×4
=(48+16+12)×2+4×4
=76×2+16
=152+16
=168(平方分米)
16.852dm2
【分析】长方体和正方体叠加后,会减少了两个面的面积,即2个边长为6dm的正方形的面积;利用长方体的表面积公式和正方体的表面积公式,分别求出长方体和正方体的表面积,用长方体的表面积加上正方体的表面积,再减去2个正方形的面积,即可求出组合图形的表面积。【来源:21·世纪·教育·网】
【详解】(9×6×2+9×20×2+6×20×2)+6×6×6-6×6×2
=(108+360+240)+216-72
=708+216-72
=852(dm2)
17.88m2
【分析】通过观察图形可知,由于两个长方体和一个正方体粘合在一起,把中间正方体的上面向上平移,左边长方体比正方体高出部分的面补在前面,同理右边长方体比正方体高出部分的面补在后面,如下图,所以整个图形的表面积相当于一个长为6m,宽为2m,高为4m的长方体表面积,长方体表面积=(长×宽+长×高+长×高)×2,据此解答。
【详解】据分析可知,组合图形的表面积为:
(6×4+6×2+4×2)×2
=(24+12+8)×2
=44×2
=88(m2)
18.232m2
【分析】由图可知,该几何体是由一个大长方体的表面积减去两个长(6-2)m和宽(4-2)m的长方形的面积,根据长方体的表面积公式,代入数据进行解答即可。
【详解】(10×6+10×4+4×6)×2
=(60+40+24)×2
=124×2
=248(m2)
2×(6-2)×(4-2)
=2×4×2
=8×2
=16(m2)
248-16=232(m2)
19.168平方厘米
【分析】观察图形可知,上面正方体与下面长方体之间被遮掉了两个完全相同的正方形,所以该组合图形的表面积可以理解为长方体的表面积与正方体侧面4个面的面积之和。
【详解】(8×2+8×6+2×6)×2+2×2×4
=(16+48+12)×2+4×4
=76×2+16
=152+16
=168(平方厘米)
20.424 cm2
【分析】通过观察图形可知,由于大小两个长方体粘合在一起,把小长方体的右面平移到大长方体的右面(即粘合处),这样大长方体的表面积是6个面的面积之和,而右边小长方体的表面积只求它的前后面、上下面共4个面的面积之和,然后相加,就是组合图形的表面积。长方体的表面积=(长×宽+长×高+宽×高)×2。21cnjy.com
【详解】(6×10+6×5+10×5)×2
=(60+30+50)×2
=140×2
=280(cm2)
(6×2+6×10)×2
=(12+60)×2
=72×2
=144(cm2)
280+144=424(cm2)
21.88cm2
【分析】由图分析,图形的表面积等于下面这个长方体的表面积加上上面这个正方体的前、后、左、右四个面的面积。据此解答即可。2-1-c-n-j-y
【详解】(6×3+3×2+2×6)×2+2×2×4
=(18+6+12)×2+16
=72+16
=88(cm2)
22.294cm2
【分析】零件的表面积可以看作一个长10cm、宽5cm、高(5+2)cm的长方体的表面积减去4个边长为2cm的小正方形的面积;长方体的表面积=(长×宽+长×高+宽×高)×2,正方形的面积=边长×边长,据此解答。21教育网
【详解】长方体的高:5+2=7(cm)
长方体的表面积:
(10×5+10×7+5×7)×2
=(50+70+35)×2
=155×2
=310(cm2)
4个小正方形的面积:
2×2×4
=4×4
=16(cm2)
零件的表面积:310-16=294(cm2)
23.288平方分米
【分析】如图,这是一个由小正方体堆砌而成的组合体,缺一角之后,缺的位置又露出3个面来,所以整体恰好相当于原来长方体的表面积。小正方体的棱长为3分米,可结合具体数据列式。
【详解】3×3=9(分米)
3×2=6(分米)
(9×6+9×6+6×6)×2
=(54+54+36)×2
=144×2
=288(平方分米)
【点睛】不要在没充分理解题意的情况下就列式,经过仔细分析之后,会发现表面积与拿走一块小正方体之前相等,只是体积减少了。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
(核心素养运用能力)第三单元长方体和正方体(表面积切拼 组合体计算)-2024-2025学年五年级数学下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、计算题
1.计算下图的表面积。(单位:分米)
2.计算下面图形的表面积。(单位:dm)
3.计算下面图形的表面积。(单位:cm)
4.计算如图图形的表面积。(单位:cm)
5.计算下面图形的表面积。
(1)
(2)
6.计算下面图形的表面积。
(1) (2)
7.求出下面几何体的表面积。
8.计算下图的表面积。(单位:分米)
9.计算下面立体图形的表面积和体积。(单位:dm)
10.计算这个零件的表面积。(单位:厘米)
11.计算组合图形的表面积。
12.从一个正方体木块中间挖去一个长3dm、宽2dm、高2dm的长方体木块,求剩下木块的表面积。
13.计算下面几何体的表面积。
14.计算下面图形的表面积。(单位:cm)
15.求出下面图形的表面积。(单位:分米)
16.求下面图形的表面积。
17.计算下面组合图形的表面积。
18.求出下列图形的表面积。
19.求下面组合图形的表面积。(单位:厘米)
20.计算下面组合图形的表面积。(单位:cm)
21.计算下面图形的表面积,单位(cm)。
22.有一个形状如下的零件,求它的表面积。(单位:cm)
23.计算下面图形的表面积。(单位:dm)
《(核心素养运用能力)第三单元长方体和正方体(表面积切拼 组合体计算)-2024-2025学年五年级数学下册人教版》参考答案21世纪教育网版权所有
1.844平方分米
【分析】根据图示,组合图形的表面积=长方体表面积+正方体表面积,依据长方体表面积公式:长方体表面积=(长×宽+长×高+宽×高)×2,因为正方体有一个面是与长方体相接的,所以只有4个面,所以,可以直接计算4个面的面积。最后将得出的结果相加即可。
【详解】长方形的表面积:
(15×10+15×8+10×8)×2
=(150+120+80)×2
=350×2
=700(平方分米)
正方体的表面积:
6×6×4
=36×4
=144(平方分米)
700+144=844(平方分米)
图形的表面积为844平方分米。
2.1020dm2
【分析】图形的表面积等于长是20dm、宽是6dm、高是15dm的长方体的表面积加上长是6dm、宽是20-7×2=6(dm)的两个正方形的面积,再减去边长为6dm的两个正方形的面积;所以图形的表面积就是长是20dm、宽是6dm、高是15dm的长方体的表面积;根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】20-7×2
=20-14
=6(dm)
(20×6+20×15+15×6)×2
=(120+300+90)×2
=(420+90)×2
=510×2
=1020(dm2)
3.306cm2
【分析】观察图形可知,组合体的表面积=长10cm,宽7cm,高3cm的长方体的表面积+四个棱长是4cm的正方形的面积。根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,正方形面积公式:面积=边长×边长,代入数据,即可解答。
【详解】(10×7+10×3+7×3)×2+4×4×4
=(70+30+21)×2+16×4
=(100+21)×2+64
=121×2+64
=242+64
=306(cm2)
组合体表面积是306cm2。
4.306cm2
【分析】由于正方体与长方体有重合面,相当于少了2个正方形的面积,所以上面的正方体只求4个侧面的面积,下面的长方体求出表面积,然后相加即可求出组合图形的表面积。
正方体表面积=棱长×棱长×6;长方体表面积=(长×宽+长×高+宽×高)×2。
【详解】4×4×4+(10×7+10×3+7×3)×2
=16×4+(70+30+21)×2
=64+121×2
=64+242
=306(cm2)
它的表面积是306cm2。
5.(1)150cm2
(2)432m2
【分析】(1)根据正方形边长=周长÷4,求出底面边长,可知这是一个正方体,根据正方体表面积=棱长×棱长×6,列式计算即可;21·cn·jy·com
(2)看图可知,在长方体的顶点挖去一个长方体,看上去表面积少了3个面,里面又出现了同样的3个面,因此这个立体图形的表面积就是完整的长方体表面积,根据长方体表面积=(长×宽+长×高+宽×高)×2,列式计算即可。2·1·c·n·j·y
【详解】(1)20÷4=5(cm)
5×5×6=150(cm2)
正方体的表面积是150cm2。
(2)(12×6+12×8+6×8)×2
=(72+96+48)×2
=216×2
=432(m2)
这个立体图形的表面积是432m2。
6.(1)
(2)
【分析】(1)根据长方体的表面积=(长×宽+长×高+宽×高)×2,带入数据计算即可;
(2)长方体上底面少了一个正方形,把上面正方体的上底面移到下底面即可拼成一个完整的长方体的表面积和上面正方体的四个侧面即四个正方形,即用长方体的表面积加上4个正方形的面积即可。21·世纪*教育网
【详解】(1)
(2)
7.216cm2
【分析】观察图形可知,这个几何体虽然切去了一块,但是通过面的平移可得:这个几何体的表面积等于棱长为6cm的正方体的表面积。正方体的表面积=棱长×棱长×6,据此解答。
【详解】6×6×6=216(cm2)
则这个几何体的表面积是216cm2。
8.248平方分米
【分析】表面积是指物体外表面积,通常是指物体表面的总面积。上面的两个小长方形和凹进去的长方形合在一起恰好就是一个长方体的表面积。则表面积=长方体的表面积+4个长方形的面积+4个小正方形的面积。长方体的表面积=(长×宽+长×高+宽×高)×2,小长方形的长是6分米,宽是2分米,面积=长×宽。正方形的边长是2分米,面积=边长×边长。www-2-1-cnjy-com
【详解】
=
=
=(平方分米)
(平方分米)
(平方分米)
(平方分米)
则图形的表面积是248平方分米。
9.150;109
【分析】由图可知:在正方体的顶点处去掉一个小长方体,虽然体积减少了,但是表面积不变。根据正方体的表面积公式:S=6a2,体积公式:V=a3,长方体的体积公式:V=abh,把数据分别代入公式解答即可。【来源:21cnj*y.co*m】
【详解】
=25×6
=150()
=25×5
=125()
=8×2
=16()
V:125-16=109()
故立体图形的表面积是150,体积是109。
【点睛】此题主要考查正方体的表面积公式、体积公式、长方体的体积公式的灵活运用,关键是熟记公式。
10.260平方厘米
【分析】在长10厘米、宽8厘米、高1厘米的长方体放上一个棱长为4厘米的正方体,则表面积比原来长方体多了4个正方形面,每个正方形的边长是4厘米,根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(10×8+10×1+8×1)×2+4×4×4即可求出这个零件的表面积。www.21-cn-jy.com
【详解】(10×8+10×1+8×1)×2+4×4×4
=(80+10+8)×2+4×4×4
=98×2+4×4×4
=196+64
=260(平方厘米)
这个零件的表面积是260平方厘米。
11.428cm2
【分析】观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;21*cnjy*com
组合图形的表面积=长方体的表面积+正方体的4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算即可。
【详解】长方体的表面积:
(10×8+10×7+8×7)×2
=(80+70+56)×2
=206×2
=412(cm2)
正方体4个面的面积:
2×2×4
=4×4
=16(cm2)
一共:412+16=428(cm2)
组合图形的表面积是428cm2。
12.170dm2
【分析】在一个大正方体里,挖去一个长方体,表面积增加了,是原来的正方体表面积再加上小长方体的前后左右4个面。【出处:21教育名师】
【详解】正方体的表面积:5×5×6
=25×6
=150(dm2)
长方体的表面积:(3×2+2×2)×2
=(6+4)×2
=10×2
=20(dm2)
150+20=170(dm2)
剩下木块的表面积是170dm2。
13.33.4m2
【分析】如图:
观察图形可知,两个长方体有重合的部分,把小长方体的上面向下平移,补给大长方体的上面;这样大长方体的表面积是6个面的面积之和,而小长方体只需计算4个面(前后面和左右面)的面积。【版权所有:21教育】
组合图形的表面积=小长方体4个面的面积+大长方体的表面积,小长方体4个面的面积=(长×高+宽×高)×2,大长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。21教育名师原创作品
【详解】(1.2×1+2.5×1)×2+(3×2.5+3×1+2.5×1)×2
=(1.2+2.5)×2+(7.5+3+2.5)×2
=3.7×2+13×2
=7.4+26
=33.4(m2)
几何体的表面积是33.4m2。
14.150cm2
【分析】观察图形可知,正方体与长方体有重合的部分,把正方体的上面向下平移,补给长方体的上面;这样长方体的表面积是6个面的面积之和,而正方体只需计算4个面(前后面和左右面)的面积;所以组合图形的表面积=长方体的表面积+正方体的4个面的面积,根据长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个面的面积=棱长×棱长×4,代入数据计算即可。21*cnjy*com
【详解】长方体的表面积:
(8×3+8×3+3×3)×2
=(24+24+9)×2
=57×2
=114(cm2)
正方体4个面的面积:
3×3×4
=9×4
=36(cm2)
一共:114+36=150(cm2)
图形的表面积是150cm2。
15.168平方分米
【分析】观察组合图形可得:组合图形表面积=长方体表面积+正方体的4个面的面积。
【详解】(8×6+8×2+2×6)×2+2×2×4
=(48+16+12)×2+4×4
=76×2+16
=152+16
=168(平方分米)
16.852dm2
【分析】长方体和正方体叠加后,会减少了两个面的面积,即2个边长为6dm的正方形的面积;利用长方体的表面积公式和正方体的表面积公式,分别求出长方体和正方体的表面积,用长方体的表面积加上正方体的表面积,再减去2个正方形的面积,即可求出组合图形的表面积。【来源:21·世纪·教育·网】
【详解】(9×6×2+9×20×2+6×20×2)+6×6×6-6×6×2
=(108+360+240)+216-72
=708+216-72
=852(dm2)
17.88m2
【分析】通过观察图形可知,由于两个长方体和一个正方体粘合在一起,把中间正方体的上面向上平移,左边长方体比正方体高出部分的面补在前面,同理右边长方体比正方体高出部分的面补在后面,如下图,所以整个图形的表面积相当于一个长为6m,宽为2m,高为4m的长方体表面积,长方体表面积=(长×宽+长×高+长×高)×2,据此解答。
【详解】据分析可知,组合图形的表面积为:
(6×4+6×2+4×2)×2
=(24+12+8)×2
=44×2
=88(m2)
18.232m2
【分析】由图可知,该几何体是由一个大长方体的表面积减去两个长(6-2)m和宽(4-2)m的长方形的面积,根据长方体的表面积公式,代入数据进行解答即可。
【详解】(10×6+10×4+4×6)×2
=(60+40+24)×2
=124×2
=248(m2)
2×(6-2)×(4-2)
=2×4×2
=8×2
=16(m2)
248-16=232(m2)
19.168平方厘米
【分析】观察图形可知,上面正方体与下面长方体之间被遮掉了两个完全相同的正方形,所以该组合图形的表面积可以理解为长方体的表面积与正方体侧面4个面的面积之和。
【详解】(8×2+8×6+2×6)×2+2×2×4
=(16+48+12)×2+4×4
=76×2+16
=152+16
=168(平方厘米)
20.424 cm2
【分析】通过观察图形可知,由于大小两个长方体粘合在一起,把小长方体的右面平移到大长方体的右面(即粘合处),这样大长方体的表面积是6个面的面积之和,而右边小长方体的表面积只求它的前后面、上下面共4个面的面积之和,然后相加,就是组合图形的表面积。长方体的表面积=(长×宽+长×高+宽×高)×2。21cnjy.com
【详解】(6×10+6×5+10×5)×2
=(60+30+50)×2
=140×2
=280(cm2)
(6×2+6×10)×2
=(12+60)×2
=72×2
=144(cm2)
280+144=424(cm2)
21.88cm2
【分析】由图分析,图形的表面积等于下面这个长方体的表面积加上上面这个正方体的前、后、左、右四个面的面积。据此解答即可。2-1-c-n-j-y
【详解】(6×3+3×2+2×6)×2+2×2×4
=(18+6+12)×2+16
=72+16
=88(cm2)
22.294cm2
【分析】零件的表面积可以看作一个长10cm、宽5cm、高(5+2)cm的长方体的表面积减去4个边长为2cm的小正方形的面积;长方体的表面积=(长×宽+长×高+宽×高)×2,正方形的面积=边长×边长,据此解答。21教育网
【详解】长方体的高:5+2=7(cm)
长方体的表面积:
(10×5+10×7+5×7)×2
=(50+70+35)×2
=155×2
=310(cm2)
4个小正方形的面积:
2×2×4
=4×4
=16(cm2)
零件的表面积:310-16=294(cm2)
23.288平方分米
【分析】如图,这是一个由小正方体堆砌而成的组合体,缺一角之后,缺的位置又露出3个面来,所以整体恰好相当于原来长方体的表面积。小正方体的棱长为3分米,可结合具体数据列式。
【详解】3×3=9(分米)
3×2=6(分米)
(9×6+9×6+6×6)×2
=(54+54+36)×2
=144×2
=288(平方分米)
【点睛】不要在没充分理解题意的情况下就列式,经过仔细分析之后,会发现表面积与拿走一块小正方体之前相等,只是体积减少了。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
