1.2 圆柱的表面积(同步练习)(含答案)--2024-2025学年六年级数学下册(北师大版)
文档属性
| 名称 | 1.2 圆柱的表面积(同步练习)(含答案)--2024-2025学年六年级数学下册(北师大版) | 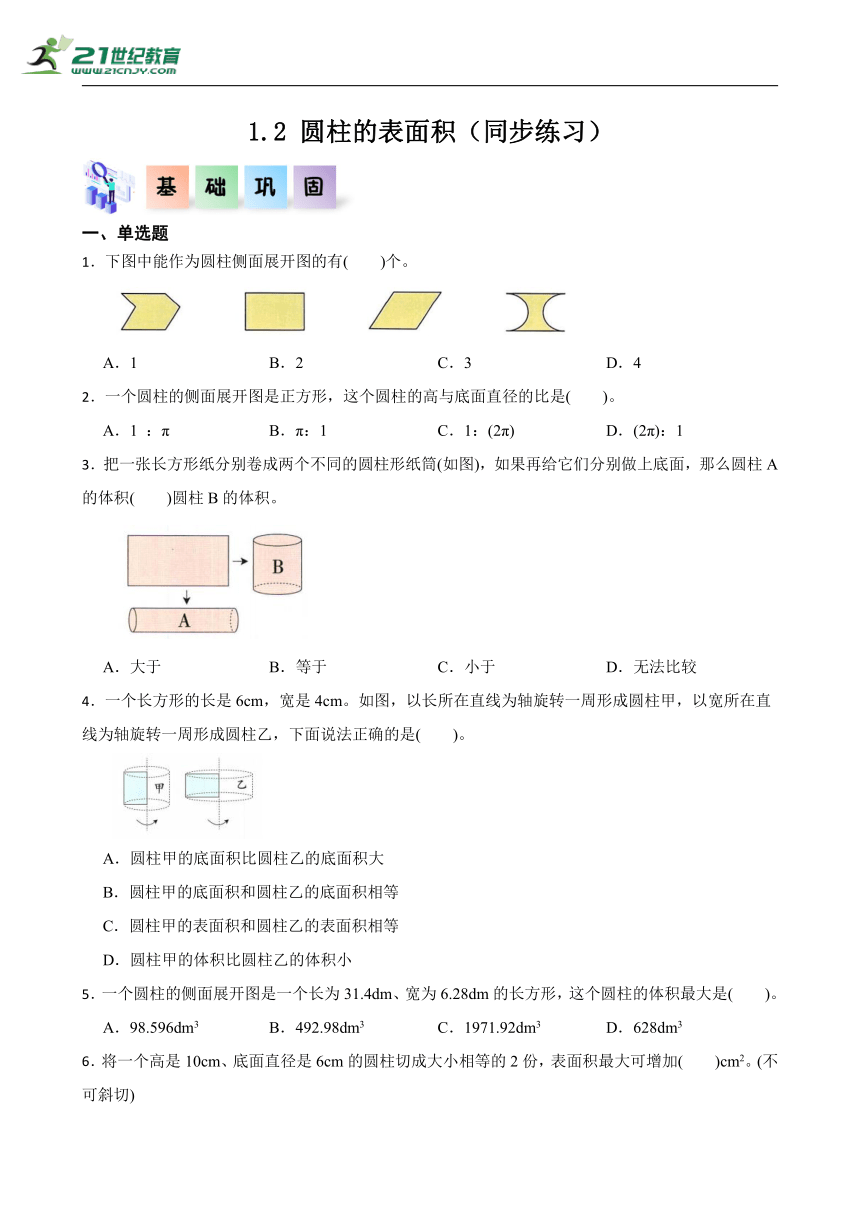 | |
| 格式 | docx | ||
| 文件大小 | 450.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 07:49:49 | ||
图片预览



文档简介
1.2 圆柱的表面积(同步练习)
一、单选题
1.下图中能作为圆柱侧面展开图的有( )个。
A.1 B.2 C.3 D.4
2.一个圆柱的侧面展开图是正方形,这个圆柱的高与底面直径的比是( )。
A.1 :π B.π:1 C.1:(2π) D.(2π):1
3.把一张长方形纸分别卷成两个不同的圆柱形纸筒(如图),如果再给它们分别做上底面,那么圆柱A的体积( )圆柱B的体积。
A.大于 B.等于 C.小于 D.无法比较
4.一个长方形的长是6cm,宽是4cm。如图,以长所在直线为轴旋转一周形成圆柱甲,以宽所在直线为轴旋转一周形成圆柱乙,下面说法正确的是( )。
A.圆柱甲的底面积比圆柱乙的底面积大
B.圆柱甲的底面积和圆柱乙的底面积相等
C.圆柱甲的表面积和圆柱乙的表面积相等
D.圆柱甲的体积比圆柱乙的体积小
5.一个圆柱的侧面展开图是一个长为31.4dm、宽为6.28dm的长方形,这个圆柱的体积最大是( )。
A.98.596dm3 B.492.98dm3 C.1971.92dm3 D.628dm3
6.将一个高是10cm、底面直径是6cm的圆柱切成大小相等的2份,表面积最大可增加( )cm2。(不可斜切)
A.28.26 B.56.52 C.60 D.120
7.如果圆柱的底面直径扩大到原来的2倍,高缩小到原来的 那么圆柱的侧面积( )。
A.扩大到原来的2倍 B.缩小到原来的
C.不变 D.不确定
8.一个侧面积为 底面半径为5cm的圆柱的高是( )cm。
A.10 B.5 C.20 D.4
二、判断题
9.侧面积相等的两个圆柱体,底面积也一定相等。( )
10.用一张长方形的硬纸板分别横着和竖着卷成两个圆柱,这两个圆柱的体积一样大。( )
11.两个圆柱的侧面积相等,它们的高一定也相等。( )
12.圆柱的底面直径是3cm,高是9.42cm,它的侧面展开后一定是一个正方形。( )
13.将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形.( )
三、填空题
14.手工课上,云云将两段同样的圆柱形木块叠放在一起,表面积减少了25.12cm2,若每个小圆柱的高是5cm,则叠放后的圆柱的表面积是 cm2,体积是 cm3。
15.一进实验小学校门,就能看到大厅有8根同样大小的圆柱形大理石柱,每根柱子的底面半径是5dm,高是4m,若安排学生擦这些柱子,则要擦的面积是 m2。
16.压路机的滚筒是一个圆柱体,横截面的半径是0.5m,长是1.6m。如果这个压路机以每分钟转动12圈的速度前进,5分钟能压路面 m2。
17.把3个大小完全相同,长都是0.2m的小圆柱拼成一个大圆柱后,表面积减少了12.56dm2,拼成的大圆柱的体积是 dm3,表面积是 dm2。
18.如图,将一个圆柱形饮料罐的侧面商标沿虚线剪开,展开后得到一个面积为 的平行四边形,这个饮料罐的底面周长是 cm,体积是 cm3。
19.一个底面半径为2.5cm的圆柱的侧面沿高展开是正方形,这个圆柱的高是 cm,侧面积是 cm2。
四、操作题
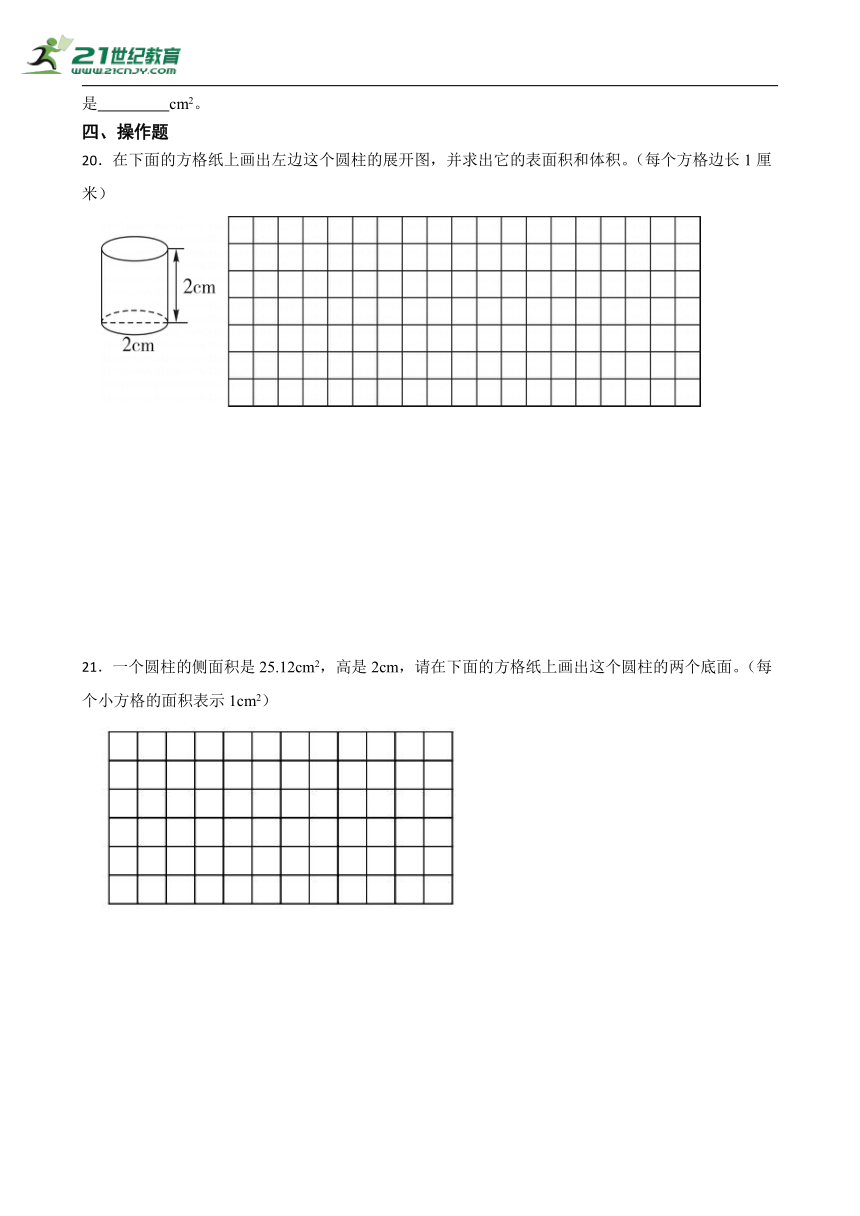
20.在下面的方格纸上画出左边这个圆柱的展开图,并求出它的表面积和体积。(每个方格边长1厘米)
21.一个圆柱的侧面积是25.12cm2,高是2cm,请在下面的方格纸上画出这个圆柱的两个底面。(每个小方格的面积表示1cm2)
五、解决问题
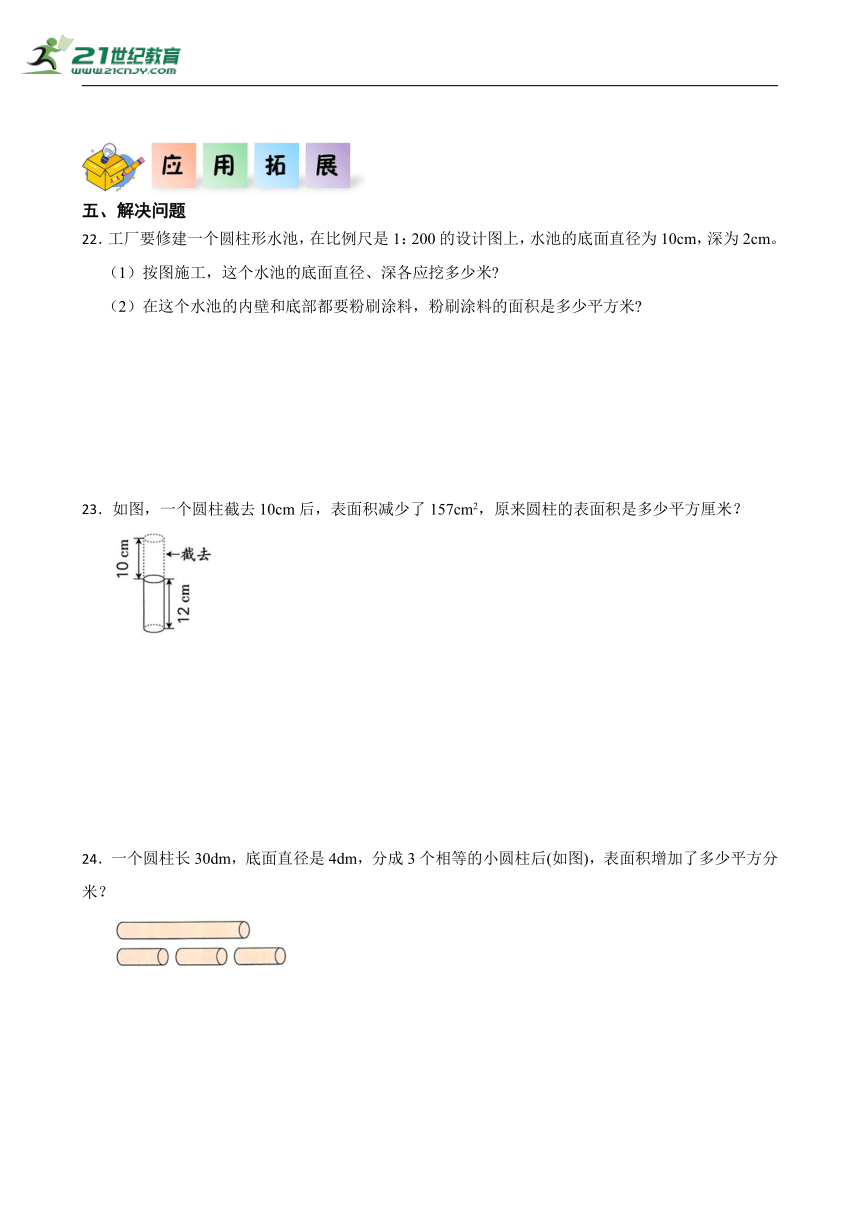
22.工厂要修建一个圆柱形水池,在比例尺是1:200的设计图上,水池的底面直径为10cm,深为2cm。
(1)按图施工,这个水池的底面直径、深各应挖多少米
(2)在这个水池的内壁和底部都要粉刷涂料,粉刷涂料的面积是多少平方米
23.如图,一个圆柱截去10cm后,表面积减少了157cm2,原来圆柱的表面积是多少平方厘米?
24.一个圆柱长30dm,底面直径是4dm,分成3个相等的小圆柱后(如图),表面积增加了多少平方分米?
25.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆形。
(1)这个大棚的占地面积是多少平方米?
(2)覆盖这个大棚的薄膜约有多少平方米?
26.有一个圆柱体的零件,高12厘米,底面直径是8厘米,零件的一端有一个圆柱形的直孔,如图:圆孔的直径是6厘米,孔深7厘米。如果将这个零件接触空气的部分涂上防锈漆,一共需涂多少平方厘米?
答案解析部分
1.C
2.B
3.C
4.D
5.B
6.D
7.C
8.A
9.错误
解:侧面积相等的两个圆柱体,底面积不一定相等,所以原题干说法错误。
故答案为:错误。
因为圆柱的侧面积=底面周长×高=2×圆周率×半径×高,底面积=圆周率×半径的平方,因此当两个圆柱的侧面积相等时,它们的底面周长不一定相等,即半径不一定相等,所以,底面积就不一定相等。
10.错误
解:用一张长方形的硬纸板分别横着和竖着卷成两个圆柱,这两个圆柱的体积不一样大,原题干说法错误。
故答案为:错误。
用一张长方形的硬纸板卷成一个圆柱,则这张长方形硬纸板的长和宽就分别是圆柱的底面周长和高,因为长方形的长不等于宽,所以横着和竖着卷成的两个圆柱的底面周长不相等,底面周长=2πr,即底面半径就不相等,因此它们的底面积不相等,同时高也不相等,所以,这两个圆柱的体积就不一样大。
11.错误
解:两个圆柱的侧面积相等,侧面积的大小是由底面周长和高两个因素共同决定的。因此,如果两个圆柱的侧面积相等,并不意味着它们的底面周长和高也一定相等。实际上,只要底面周长和高的乘积相等,两个圆柱的侧面积就可以相等。
故答案为:错误。
圆柱的侧面积=底面周长×高,底面周长=π×直径,圆柱的侧面积与底面半径和高有关。
12.错误
解:3.14×3=9.42(厘米),这个圆柱沿高剪开后是正方形,原题干说法错误。
故答案为:错误。
圆柱的底面周长=π×直径=圆柱的高,只有这个圆柱沿高剪开后是正方形。
13.正确
解:将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形。原题说法正确。
故答案为:正确。
圆柱的底面周长和高不相等,圆柱的侧面沿着高展开后就是长方形;底面周长和高相等,圆柱的侧面展开后就是正方形;如果沿着侧面斜着展开后就是平行四边形。
14.150.72;125.6
15.100.48
16.301.44
17.18.84;43.96
18.18.84;282.6
19.15.7;246.49
20.解:3.14×2=6.28(cm)
2÷2=1(cm)
表面积:3.14×12×2+3.14×2×2
=3.14×1×2+3.14×2×2
=6.28+12.56
=18.84(cm2)
体积:3.14×12×2
=3.14×1×2
=3.14×2
=6.28(cm3)
圆柱的展开图是一个长方形和两个相等的圆,长方形的长是圆的底面周长,据此先求出长方形的长,再画出展开图;
圆柱的表面积=侧面积+底面积×2,圆柱的体积=底面积×高,据此列式解答。
21.25.12÷2÷3.14
=12.56÷3.14
=4(厘米)
圆柱的底面直径=侧面积÷高÷π,这个圆柱的两个底面直径都是4厘米,即直径画4格。
22.(1)直径:10÷
=10×200
=2000(厘米)=20(米)
深:2÷
=2×200
=400(厘米)=4(米)
答:按图施工,这个水池的底面直径应挖20米,深应挖4米。
(2)解:20×3.14×4+3.14×(20÷2)2
=251.2+314
=565.2(平方米)
答:粉刷涂料的面积是565.2平方米。
(1)实际距离=图上距离÷比例尺,代入数值计算即可;(2)粉刷涂料的面积=直径×π×深+π×(直径÷2)2,代入数值计算即可。
23.157÷10=15.7(cm)
15.7÷3.14÷2=2.5(cm)
答:原来圆柱的表面积是384.65cm2。
24.答:表面积增加了50.24dm2。
25.(1)解:20×(2×2)
=20×4
=80(平方米)
答:这个大棚的占地面积是80平方米。
(2)解:3.14×2×2×20÷2
=12.56×20÷2
=251.2÷2
=125.6(平方米)
3.14×22=12.56(平方米)
125.6+12.56=138.16(平方米)
答:覆盖这个大棚的薄膜约有138.16平方米。
(1)看图及根据题意可知这个大棚的占地面是一个长为大棚长、宽为大棚底面直径的长方形,因此,大棚长×(横截面半径×2)=大棚的占地面积;
(2)看图可知大棚覆盖薄膜的面积是圆柱侧面积的一半及两个半圆形的面积的和,而两个半圆形可以合成一个圆,所以,圆周率×半径×2×大棚长÷2=大棚侧面积,圆周率×半径的平方=两个半圆形的面积,大棚侧面积+两个半圆形的面积=大棚薄膜的面积。
26.解:3.14×8×12
=25.12×12
=301.44(平方厘米)
3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
3.14×6×7
=18.84×7
=131.88(平方厘米)
301.44+50.24×2+131.88
=301.44+100.48+131.88
=401.92+131.88
=533.8(平方厘米)
答:一共需涂533.8平方厘米。
根据题意及看图可知将直孔的下底面平移到上面,则零件接触空气的部分就包括了外面圆柱的侧面和两个底面及直孔的侧面:圆周率×外面圆柱的直径×外面圆柱的高=外面圆柱的侧面积,圆周率×(外面圆柱的直径÷2)2=外面圆柱的底面积,圆周率×直孔的直径×直孔的深=直孔的侧面积,外面圆柱的侧面积+外面圆柱的底面积×2+直孔的侧面积=需要涂防锈漆的面积。
一、单选题
1.下图中能作为圆柱侧面展开图的有( )个。
A.1 B.2 C.3 D.4
2.一个圆柱的侧面展开图是正方形,这个圆柱的高与底面直径的比是( )。
A.1 :π B.π:1 C.1:(2π) D.(2π):1
3.把一张长方形纸分别卷成两个不同的圆柱形纸筒(如图),如果再给它们分别做上底面,那么圆柱A的体积( )圆柱B的体积。
A.大于 B.等于 C.小于 D.无法比较
4.一个长方形的长是6cm,宽是4cm。如图,以长所在直线为轴旋转一周形成圆柱甲,以宽所在直线为轴旋转一周形成圆柱乙,下面说法正确的是( )。
A.圆柱甲的底面积比圆柱乙的底面积大
B.圆柱甲的底面积和圆柱乙的底面积相等
C.圆柱甲的表面积和圆柱乙的表面积相等
D.圆柱甲的体积比圆柱乙的体积小
5.一个圆柱的侧面展开图是一个长为31.4dm、宽为6.28dm的长方形,这个圆柱的体积最大是( )。
A.98.596dm3 B.492.98dm3 C.1971.92dm3 D.628dm3
6.将一个高是10cm、底面直径是6cm的圆柱切成大小相等的2份,表面积最大可增加( )cm2。(不可斜切)
A.28.26 B.56.52 C.60 D.120
7.如果圆柱的底面直径扩大到原来的2倍,高缩小到原来的 那么圆柱的侧面积( )。
A.扩大到原来的2倍 B.缩小到原来的
C.不变 D.不确定
8.一个侧面积为 底面半径为5cm的圆柱的高是( )cm。
A.10 B.5 C.20 D.4
二、判断题
9.侧面积相等的两个圆柱体,底面积也一定相等。( )
10.用一张长方形的硬纸板分别横着和竖着卷成两个圆柱,这两个圆柱的体积一样大。( )
11.两个圆柱的侧面积相等,它们的高一定也相等。( )
12.圆柱的底面直径是3cm,高是9.42cm,它的侧面展开后一定是一个正方形。( )
13.将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形.( )
三、填空题
14.手工课上,云云将两段同样的圆柱形木块叠放在一起,表面积减少了25.12cm2,若每个小圆柱的高是5cm,则叠放后的圆柱的表面积是 cm2,体积是 cm3。
15.一进实验小学校门,就能看到大厅有8根同样大小的圆柱形大理石柱,每根柱子的底面半径是5dm,高是4m,若安排学生擦这些柱子,则要擦的面积是 m2。
16.压路机的滚筒是一个圆柱体,横截面的半径是0.5m,长是1.6m。如果这个压路机以每分钟转动12圈的速度前进,5分钟能压路面 m2。
17.把3个大小完全相同,长都是0.2m的小圆柱拼成一个大圆柱后,表面积减少了12.56dm2,拼成的大圆柱的体积是 dm3,表面积是 dm2。
18.如图,将一个圆柱形饮料罐的侧面商标沿虚线剪开,展开后得到一个面积为 的平行四边形,这个饮料罐的底面周长是 cm,体积是 cm3。
19.一个底面半径为2.5cm的圆柱的侧面沿高展开是正方形,这个圆柱的高是 cm,侧面积是 cm2。
四、操作题
20.在下面的方格纸上画出左边这个圆柱的展开图,并求出它的表面积和体积。(每个方格边长1厘米)
21.一个圆柱的侧面积是25.12cm2,高是2cm,请在下面的方格纸上画出这个圆柱的两个底面。(每个小方格的面积表示1cm2)
五、解决问题
22.工厂要修建一个圆柱形水池,在比例尺是1:200的设计图上,水池的底面直径为10cm,深为2cm。
(1)按图施工,这个水池的底面直径、深各应挖多少米
(2)在这个水池的内壁和底部都要粉刷涂料,粉刷涂料的面积是多少平方米
23.如图,一个圆柱截去10cm后,表面积减少了157cm2,原来圆柱的表面积是多少平方厘米?
24.一个圆柱长30dm,底面直径是4dm,分成3个相等的小圆柱后(如图),表面积增加了多少平方分米?
25.一个用塑料薄膜覆盖的蔬菜大棚,长20米,横截面是一个半径为2米的半圆形。
(1)这个大棚的占地面积是多少平方米?
(2)覆盖这个大棚的薄膜约有多少平方米?
26.有一个圆柱体的零件,高12厘米,底面直径是8厘米,零件的一端有一个圆柱形的直孔,如图:圆孔的直径是6厘米,孔深7厘米。如果将这个零件接触空气的部分涂上防锈漆,一共需涂多少平方厘米?
答案解析部分
1.C
2.B
3.C
4.D
5.B
6.D
7.C
8.A
9.错误
解:侧面积相等的两个圆柱体,底面积不一定相等,所以原题干说法错误。
故答案为:错误。
因为圆柱的侧面积=底面周长×高=2×圆周率×半径×高,底面积=圆周率×半径的平方,因此当两个圆柱的侧面积相等时,它们的底面周长不一定相等,即半径不一定相等,所以,底面积就不一定相等。
10.错误
解:用一张长方形的硬纸板分别横着和竖着卷成两个圆柱,这两个圆柱的体积不一样大,原题干说法错误。
故答案为:错误。
用一张长方形的硬纸板卷成一个圆柱,则这张长方形硬纸板的长和宽就分别是圆柱的底面周长和高,因为长方形的长不等于宽,所以横着和竖着卷成的两个圆柱的底面周长不相等,底面周长=2πr,即底面半径就不相等,因此它们的底面积不相等,同时高也不相等,所以,这两个圆柱的体积就不一样大。
11.错误
解:两个圆柱的侧面积相等,侧面积的大小是由底面周长和高两个因素共同决定的。因此,如果两个圆柱的侧面积相等,并不意味着它们的底面周长和高也一定相等。实际上,只要底面周长和高的乘积相等,两个圆柱的侧面积就可以相等。
故答案为:错误。
圆柱的侧面积=底面周长×高,底面周长=π×直径,圆柱的侧面积与底面半径和高有关。
12.错误
解:3.14×3=9.42(厘米),这个圆柱沿高剪开后是正方形,原题干说法错误。
故答案为:错误。
圆柱的底面周长=π×直径=圆柱的高,只有这个圆柱沿高剪开后是正方形。
13.正确
解:将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形。原题说法正确。
故答案为:正确。
圆柱的底面周长和高不相等,圆柱的侧面沿着高展开后就是长方形;底面周长和高相等,圆柱的侧面展开后就是正方形;如果沿着侧面斜着展开后就是平行四边形。
14.150.72;125.6
15.100.48
16.301.44
17.18.84;43.96
18.18.84;282.6
19.15.7;246.49
20.解:3.14×2=6.28(cm)
2÷2=1(cm)
表面积:3.14×12×2+3.14×2×2
=3.14×1×2+3.14×2×2
=6.28+12.56
=18.84(cm2)
体积:3.14×12×2
=3.14×1×2
=3.14×2
=6.28(cm3)
圆柱的展开图是一个长方形和两个相等的圆,长方形的长是圆的底面周长,据此先求出长方形的长,再画出展开图;
圆柱的表面积=侧面积+底面积×2,圆柱的体积=底面积×高,据此列式解答。
21.25.12÷2÷3.14
=12.56÷3.14
=4(厘米)
圆柱的底面直径=侧面积÷高÷π,这个圆柱的两个底面直径都是4厘米,即直径画4格。
22.(1)直径:10÷
=10×200
=2000(厘米)=20(米)
深:2÷
=2×200
=400(厘米)=4(米)
答:按图施工,这个水池的底面直径应挖20米,深应挖4米。
(2)解:20×3.14×4+3.14×(20÷2)2
=251.2+314
=565.2(平方米)
答:粉刷涂料的面积是565.2平方米。
(1)实际距离=图上距离÷比例尺,代入数值计算即可;(2)粉刷涂料的面积=直径×π×深+π×(直径÷2)2,代入数值计算即可。
23.157÷10=15.7(cm)
15.7÷3.14÷2=2.5(cm)
答:原来圆柱的表面积是384.65cm2。
24.答:表面积增加了50.24dm2。
25.(1)解:20×(2×2)
=20×4
=80(平方米)
答:这个大棚的占地面积是80平方米。
(2)解:3.14×2×2×20÷2
=12.56×20÷2
=251.2÷2
=125.6(平方米)
3.14×22=12.56(平方米)
125.6+12.56=138.16(平方米)
答:覆盖这个大棚的薄膜约有138.16平方米。
(1)看图及根据题意可知这个大棚的占地面是一个长为大棚长、宽为大棚底面直径的长方形,因此,大棚长×(横截面半径×2)=大棚的占地面积;
(2)看图可知大棚覆盖薄膜的面积是圆柱侧面积的一半及两个半圆形的面积的和,而两个半圆形可以合成一个圆,所以,圆周率×半径×2×大棚长÷2=大棚侧面积,圆周率×半径的平方=两个半圆形的面积,大棚侧面积+两个半圆形的面积=大棚薄膜的面积。
26.解:3.14×8×12
=25.12×12
=301.44(平方厘米)
3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
3.14×6×7
=18.84×7
=131.88(平方厘米)
301.44+50.24×2+131.88
=301.44+100.48+131.88
=401.92+131.88
=533.8(平方厘米)
答:一共需涂533.8平方厘米。
根据题意及看图可知将直孔的下底面平移到上面,则零件接触空气的部分就包括了外面圆柱的侧面和两个底面及直孔的侧面:圆周率×外面圆柱的直径×外面圆柱的高=外面圆柱的侧面积,圆周率×(外面圆柱的直径÷2)2=外面圆柱的底面积,圆周率×直孔的直径×直孔的深=直孔的侧面积,外面圆柱的侧面积+外面圆柱的底面积×2+直孔的侧面积=需要涂防锈漆的面积。
