1.4 圆锥的体积(同步练习)(含答案)--2024-2025学年六年级数学下册(北师大版)
文档属性
| 名称 | 1.4 圆锥的体积(同步练习)(含答案)--2024-2025学年六年级数学下册(北师大版) |

|
|
| 格式 | docx | ||
| 文件大小 | 544.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 07:53:48 | ||
图片预览


文档简介
1.4 圆锥的体积(同步练习)
一、单选题
1.一个圆柱和一个圆锥的底面积之比是4:9,它们的体积之比是5:6,圆柱和圆锥的高的最简单的整数比是( )。
A.5:8 B.12:5 C.8:5 D.5:12
2.下列说法正确的是( )。
A.圆柱的体积是圆锥体积的3倍
B.两个圆柱的体积相等,它们一定等底、等高
C.将一个装满水的、高是6cm的圆锥形容器中的水倒入与它等底、等高的圆柱形容器,水高3cm
D.圆柱和圆锥的高相等,底面半径之比是1:3,那么体积之比也是1:3
3.在下面四个空容器中分别注入120mL的水(水不溢出容器,容器厚度不计),容器底面尺寸如下图所示,水位最低的是( )。
A. B.
C. D.
4.圆锥的底面半径扩大到原来的3倍,高不变,体积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
5.一个圆柱和一个圆锥等底、等高,圆锥的体积是12cm3,若圆锥的高缩小到原来的 底面积不变,则圆柱与圆锥的体积之比变为( )。
A.3:1 B.9:1 C.9:2 D.1 :1
6. 一个圆锥与一个圆柱的底面积与体积分别相等,圆柱的高是6厘米,那么圆锥的高是( )厘米。
A.3 B.27 C.18 D.24
7.一个等腰直角三角形,以一条直角边所在的直线为轴旋转一周,得到的圆锥的底面积为28.26 cm2,圆锥的高是( ) cm。
A.9 B.4.5 C.3 D.1.5
二、填空题
8.一个直角三角形,两个直角边分别是3厘米和4厘米.以直角边为轴旋转一周可以得到一个圆锥,则这个圆锥的体积最大是 立方厘米.
9.一个直角三角形的两条直角边分别长3厘米和4厘米,以这个直角三角形的一条直角边为轴旋转一圈得到一个圆锥,这个圆锥体积最大为 .
10.一个直角三角形的两条直角边长分别是3厘米和4厘米,斜边长5厘米,如果以4厘米长的直角边为轴把三角形旋转一周,得到一个圆锥体,这个圆锥体的高是 厘米,底面半径是 厘米,体积是 立方厘米.
11.端午节到了,同学们学习用芦苇叶和糯米包近似圆锥形的粽子,粽子的底面周长为18.84cm,高为5cm。每个粽子的体积是 cm3,若每立方厘米糯米重1.8g,则包100个这样的粽子大约需要糯米 g。
12.一个正方体的棱长之和是72cm,把这个正方体削成一个最大的圆锥,那么圆锥的体积是 cm3。
13.把底面周长是15.7cm、高是6cm的圆柱切拼成一个近似的长方体。这个长方体的底面积是 cm2,体积是 cm3,与这个圆柱等底、等高的圆锥的体积是 cm3。
三、操作题
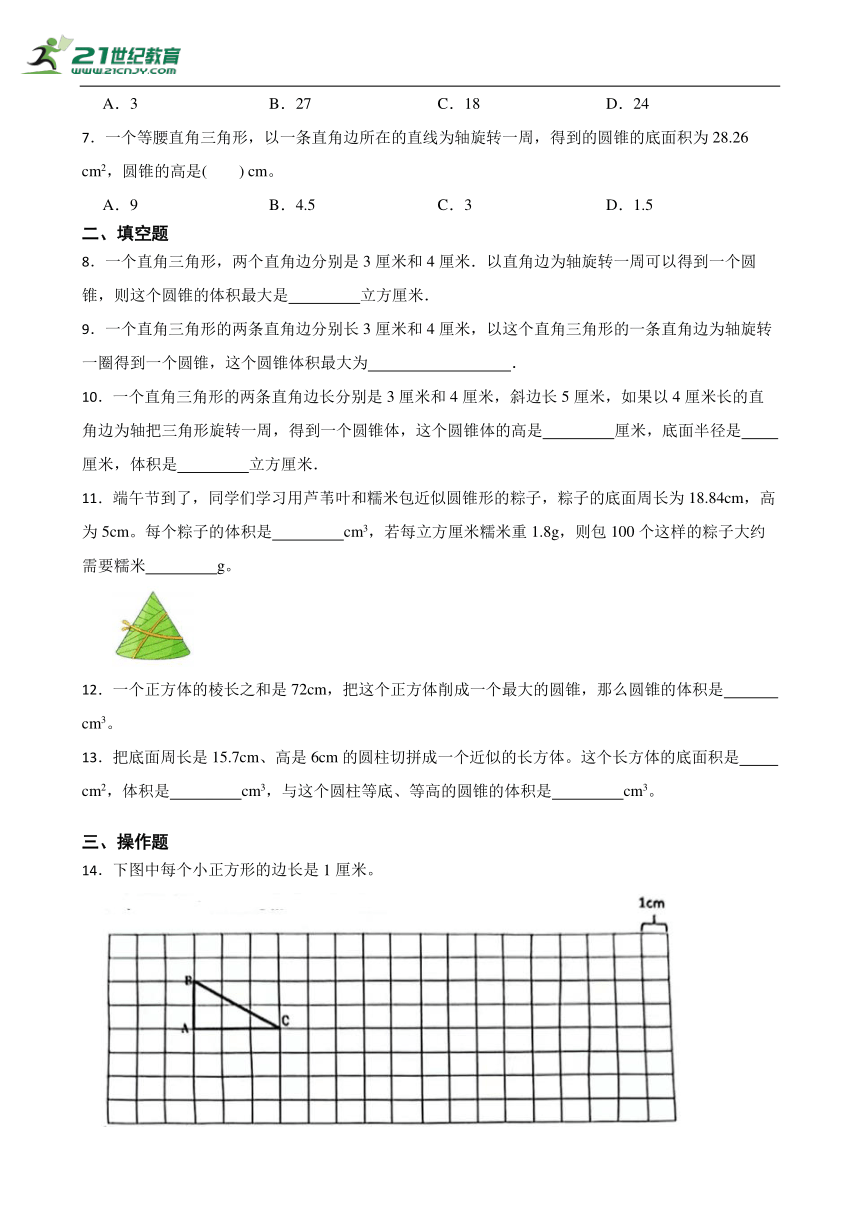
14.下图中每个小正方形的边长是1厘米。
(1)请按2∶1画出三角形 ABC 放大后的图形。
(2)如果以 AC为轴,将三角形 ABC旋转一周后,所形成的立体图形名称是 ,它体积应该是 cm3。
(3)如果三角形 ABC的每个点用数对表示,A点是(3,4),B点是(3,6),则C点是 。
(4)如图中原三角形ABC正好是一个种植园,比例尺是,那么这个种植园的实际面积应该是 平方米。
四、解决问题
15.如图,在密闭的容器(高15cm)中装有一些水,如果将这个容器倒过来,这时水面距底部的高度是多少厘米?
16.有一个底面半径为5cm的圆柱形玻璃容器,水深10cm。把一个底面半径是3cm、高是10cm的圆锥形铁块放入水中,水溢出了15.7mL,这个玻璃容器有多高?
17.底面半径是20cm、高是90cm的圆柱形容器里盛有一些水,现放入一个底面直径是20cm的圆锥形金属块,金属块沉没在水中,水面上升了5cm且未溢出。这个圆锥形金属块的高是多少厘米?
18.2024年6月25日,嫦娥六号返回器安全着陆,实现首次月球背面采样返回。返回器的形状近似于一个底面直径为1m、高为1.2m的圆锥。
(1)这个返回器的体积约为 m3。
(2)若平均每立方米约重950kg,则这个返回器约重多少千克?
19.我国古代的数学名著《九章算术》中的“商功”记载着一种求圆锥体积的方法:“下周自乘,以高乘之,三十六而一。”即用底面周长的平方乘高,再除以36,其中π取3。
(1)利用上述方法求出下图所示圆锥的体积,列式计算为: 。
(2)你能用教材所学圆锥的体积计算公式推导出此公式吗?写一写。
答案解析部分
1.A
2.D
3.C
4.C
5.B
6.C
解:6×3=18(厘米)
故答案为:C。
圆锥的体积是与它等底等高的圆柱体积的,因此,当圆锥与圆柱的底面积和体积相等,那么圆锥的高就是圆柱高的3倍;据此解答。
7.C
解:28.26÷3.14=9(平方厘米)
9÷3=3(厘米)。
故答案为:C。
圆锥的高=圆锥的底面半径,其中,底面半径的平方=圆锥的底面积÷π=9,则半径是3厘米。
8.50.24
解: ×3.14×42×3
= ×3.14×16×3
=50.24(立方厘米);
故答案为:50.24.
以3厘米的直角边为轴(也就是以4厘米的直角边为半径)旋转一周得到的圆锥的体积最大,这个圆锥的底面半径是4厘米,高是3厘米.由此计算出这个圆锥的体积.
9.50.24立方厘米
解:以3厘米的边为轴旋转一周,可以得到一个圆锥,
体积为: ×π×42×3
=16π
=50.24(立方厘米);
以4厘米的边为轴旋转一周,可以得到一个圆锥,
体积为: ×π×32×4
=12π
=37.68(立方厘米)
答:得到的是一个圆锥体,这个图形的体积最大是50.24立方厘米.
故答案为:50.24立方厘米.
分别以直角三角形的一条直角边为轴旋转一圈得到一个圆锥,有两种情况,情况一:以3厘米的边为轴旋转一周,可以得到一个底面半径是4厘米,高3厘米的圆锥;情况二:以4厘米的边为轴旋转一周,可以得到一个底面半径为3厘米,高为4厘米的圆锥,分别求出这两个圆锥的体积,进行比较后再即可解答.此题主要考查圆锥展开图的特点和圆锥体积公式的灵活应用.
10.4;3;37.68
解:以4厘米长的直角边为轴把三角形旋转一周,则这个4厘米的直角边就是得到的圆锥的高,3厘米的直角边是这个圆锥的底面半径,所以这个圆锥的体积是: ×3.14×32×4=37.68(立方厘米),
答:这个圆锥体的高是4厘米,底面半径是3厘米,体积是37.68立方厘米.
故答案为:4;3;37.68.
根据圆锥的展开图特点可得:以4厘米长的直角边为轴把三角形旋转一周,则这个4厘米的直角边就是得到的圆锥的高,另一条直角边是这个圆锥的底面半径,再利用圆锥的体积公式即可解答. 抓住圆锥的展开图特点,得出旋转后的图形是一个圆锥体且两条直角边分别是圆锥的底面半径和高,是解决此类问题的关键.
11.47.1;8478
12.56.52
13.19.625;117.75;39.25
14.(1)解:
(2)圆锥;18.84
(3)(6,4)
(4)120000
解:(2)所形成的立体图形是圆锥;
3.14×32×2÷3
=56.52÷3
=18.84(立方厘米);
(3)C点在第6列,第4行,用数对(6,4) 表示;
(4)(200×3)×(200×2)÷2
=600×400÷2
=240000÷2
=120000(平方米)。
故答案为:(2)圆锥;18.84;(3)(6,4);(4)120000。
(1)放大后三角形底、高的格数分别=原来三角形底、高的格数分别×2,然后画出三角形;
(2)所形成的立体图形是圆锥;圆锥的体积=π×半径2×高÷3;
(3)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
(4)实际距离=图上距离×每厘米代表的实际长度,这个种植园的实际面积=实际长×实际高÷2。
15.
16.15.7mL=15.7cm3
答:这个玻璃容器有11cm高。
17.6280×3÷[3.14×(20÷2)2]=60(cm)
答:这个圆锥形金属块的高是60cm。
18.(1)0.314
(2)0.314×950=298.3(kg)
答:这个返回器约重298.3kg。
19.(1)
(2)设圆锥的底面半径为r,高为h,底面周长为C。教材体积计算公式为 C2×h,又π取3,所以
一、单选题
1.一个圆柱和一个圆锥的底面积之比是4:9,它们的体积之比是5:6,圆柱和圆锥的高的最简单的整数比是( )。
A.5:8 B.12:5 C.8:5 D.5:12
2.下列说法正确的是( )。
A.圆柱的体积是圆锥体积的3倍
B.两个圆柱的体积相等,它们一定等底、等高
C.将一个装满水的、高是6cm的圆锥形容器中的水倒入与它等底、等高的圆柱形容器,水高3cm
D.圆柱和圆锥的高相等,底面半径之比是1:3,那么体积之比也是1:3
3.在下面四个空容器中分别注入120mL的水(水不溢出容器,容器厚度不计),容器底面尺寸如下图所示,水位最低的是( )。
A. B.
C. D.
4.圆锥的底面半径扩大到原来的3倍,高不变,体积扩大到原来的( )倍。
A.3 B.6 C.9 D.27
5.一个圆柱和一个圆锥等底、等高,圆锥的体积是12cm3,若圆锥的高缩小到原来的 底面积不变,则圆柱与圆锥的体积之比变为( )。
A.3:1 B.9:1 C.9:2 D.1 :1
6. 一个圆锥与一个圆柱的底面积与体积分别相等,圆柱的高是6厘米,那么圆锥的高是( )厘米。
A.3 B.27 C.18 D.24
7.一个等腰直角三角形,以一条直角边所在的直线为轴旋转一周,得到的圆锥的底面积为28.26 cm2,圆锥的高是( ) cm。
A.9 B.4.5 C.3 D.1.5
二、填空题
8.一个直角三角形,两个直角边分别是3厘米和4厘米.以直角边为轴旋转一周可以得到一个圆锥,则这个圆锥的体积最大是 立方厘米.
9.一个直角三角形的两条直角边分别长3厘米和4厘米,以这个直角三角形的一条直角边为轴旋转一圈得到一个圆锥,这个圆锥体积最大为 .
10.一个直角三角形的两条直角边长分别是3厘米和4厘米,斜边长5厘米,如果以4厘米长的直角边为轴把三角形旋转一周,得到一个圆锥体,这个圆锥体的高是 厘米,底面半径是 厘米,体积是 立方厘米.
11.端午节到了,同学们学习用芦苇叶和糯米包近似圆锥形的粽子,粽子的底面周长为18.84cm,高为5cm。每个粽子的体积是 cm3,若每立方厘米糯米重1.8g,则包100个这样的粽子大约需要糯米 g。
12.一个正方体的棱长之和是72cm,把这个正方体削成一个最大的圆锥,那么圆锥的体积是 cm3。
13.把底面周长是15.7cm、高是6cm的圆柱切拼成一个近似的长方体。这个长方体的底面积是 cm2,体积是 cm3,与这个圆柱等底、等高的圆锥的体积是 cm3。
三、操作题
14.下图中每个小正方形的边长是1厘米。
(1)请按2∶1画出三角形 ABC 放大后的图形。
(2)如果以 AC为轴,将三角形 ABC旋转一周后,所形成的立体图形名称是 ,它体积应该是 cm3。
(3)如果三角形 ABC的每个点用数对表示,A点是(3,4),B点是(3,6),则C点是 。
(4)如图中原三角形ABC正好是一个种植园,比例尺是,那么这个种植园的实际面积应该是 平方米。
四、解决问题
15.如图,在密闭的容器(高15cm)中装有一些水,如果将这个容器倒过来,这时水面距底部的高度是多少厘米?
16.有一个底面半径为5cm的圆柱形玻璃容器,水深10cm。把一个底面半径是3cm、高是10cm的圆锥形铁块放入水中,水溢出了15.7mL,这个玻璃容器有多高?
17.底面半径是20cm、高是90cm的圆柱形容器里盛有一些水,现放入一个底面直径是20cm的圆锥形金属块,金属块沉没在水中,水面上升了5cm且未溢出。这个圆锥形金属块的高是多少厘米?
18.2024年6月25日,嫦娥六号返回器安全着陆,实现首次月球背面采样返回。返回器的形状近似于一个底面直径为1m、高为1.2m的圆锥。
(1)这个返回器的体积约为 m3。
(2)若平均每立方米约重950kg,则这个返回器约重多少千克?
19.我国古代的数学名著《九章算术》中的“商功”记载着一种求圆锥体积的方法:“下周自乘,以高乘之,三十六而一。”即用底面周长的平方乘高,再除以36,其中π取3。
(1)利用上述方法求出下图所示圆锥的体积,列式计算为: 。
(2)你能用教材所学圆锥的体积计算公式推导出此公式吗?写一写。
答案解析部分
1.A
2.D
3.C
4.C
5.B
6.C
解:6×3=18(厘米)
故答案为:C。
圆锥的体积是与它等底等高的圆柱体积的,因此,当圆锥与圆柱的底面积和体积相等,那么圆锥的高就是圆柱高的3倍;据此解答。
7.C
解:28.26÷3.14=9(平方厘米)
9÷3=3(厘米)。
故答案为:C。
圆锥的高=圆锥的底面半径,其中,底面半径的平方=圆锥的底面积÷π=9,则半径是3厘米。
8.50.24
解: ×3.14×42×3
= ×3.14×16×3
=50.24(立方厘米);
故答案为:50.24.
以3厘米的直角边为轴(也就是以4厘米的直角边为半径)旋转一周得到的圆锥的体积最大,这个圆锥的底面半径是4厘米,高是3厘米.由此计算出这个圆锥的体积.
9.50.24立方厘米
解:以3厘米的边为轴旋转一周,可以得到一个圆锥,
体积为: ×π×42×3
=16π
=50.24(立方厘米);
以4厘米的边为轴旋转一周,可以得到一个圆锥,
体积为: ×π×32×4
=12π
=37.68(立方厘米)
答:得到的是一个圆锥体,这个图形的体积最大是50.24立方厘米.
故答案为:50.24立方厘米.
分别以直角三角形的一条直角边为轴旋转一圈得到一个圆锥,有两种情况,情况一:以3厘米的边为轴旋转一周,可以得到一个底面半径是4厘米,高3厘米的圆锥;情况二:以4厘米的边为轴旋转一周,可以得到一个底面半径为3厘米,高为4厘米的圆锥,分别求出这两个圆锥的体积,进行比较后再即可解答.此题主要考查圆锥展开图的特点和圆锥体积公式的灵活应用.
10.4;3;37.68
解:以4厘米长的直角边为轴把三角形旋转一周,则这个4厘米的直角边就是得到的圆锥的高,3厘米的直角边是这个圆锥的底面半径,所以这个圆锥的体积是: ×3.14×32×4=37.68(立方厘米),
答:这个圆锥体的高是4厘米,底面半径是3厘米,体积是37.68立方厘米.
故答案为:4;3;37.68.
根据圆锥的展开图特点可得:以4厘米长的直角边为轴把三角形旋转一周,则这个4厘米的直角边就是得到的圆锥的高,另一条直角边是这个圆锥的底面半径,再利用圆锥的体积公式即可解答. 抓住圆锥的展开图特点,得出旋转后的图形是一个圆锥体且两条直角边分别是圆锥的底面半径和高,是解决此类问题的关键.
11.47.1;8478
12.56.52
13.19.625;117.75;39.25
14.(1)解:
(2)圆锥;18.84
(3)(6,4)
(4)120000
解:(2)所形成的立体图形是圆锥;
3.14×32×2÷3
=56.52÷3
=18.84(立方厘米);
(3)C点在第6列,第4行,用数对(6,4) 表示;
(4)(200×3)×(200×2)÷2
=600×400÷2
=240000÷2
=120000(平方米)。
故答案为:(2)圆锥;18.84;(3)(6,4);(4)120000。
(1)放大后三角形底、高的格数分别=原来三角形底、高的格数分别×2,然后画出三角形;
(2)所形成的立体图形是圆锥;圆锥的体积=π×半径2×高÷3;
(3)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
(4)实际距离=图上距离×每厘米代表的实际长度,这个种植园的实际面积=实际长×实际高÷2。
15.
16.15.7mL=15.7cm3
答:这个玻璃容器有11cm高。
17.6280×3÷[3.14×(20÷2)2]=60(cm)
答:这个圆锥形金属块的高是60cm。
18.(1)0.314
(2)0.314×950=298.3(kg)
答:这个返回器约重298.3kg。
19.(1)
(2)设圆锥的底面半径为r,高为h,底面周长为C。教材体积计算公式为 C2×h,又π取3,所以
