4.2 正比例(同步练习)(含答案)--2024-2025学年六年级数学下册(北师大版)
文档属性
| 名称 | 4.2 正比例(同步练习)(含答案)--2024-2025学年六年级数学下册(北师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 223.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 08:01:21 | ||
图片预览


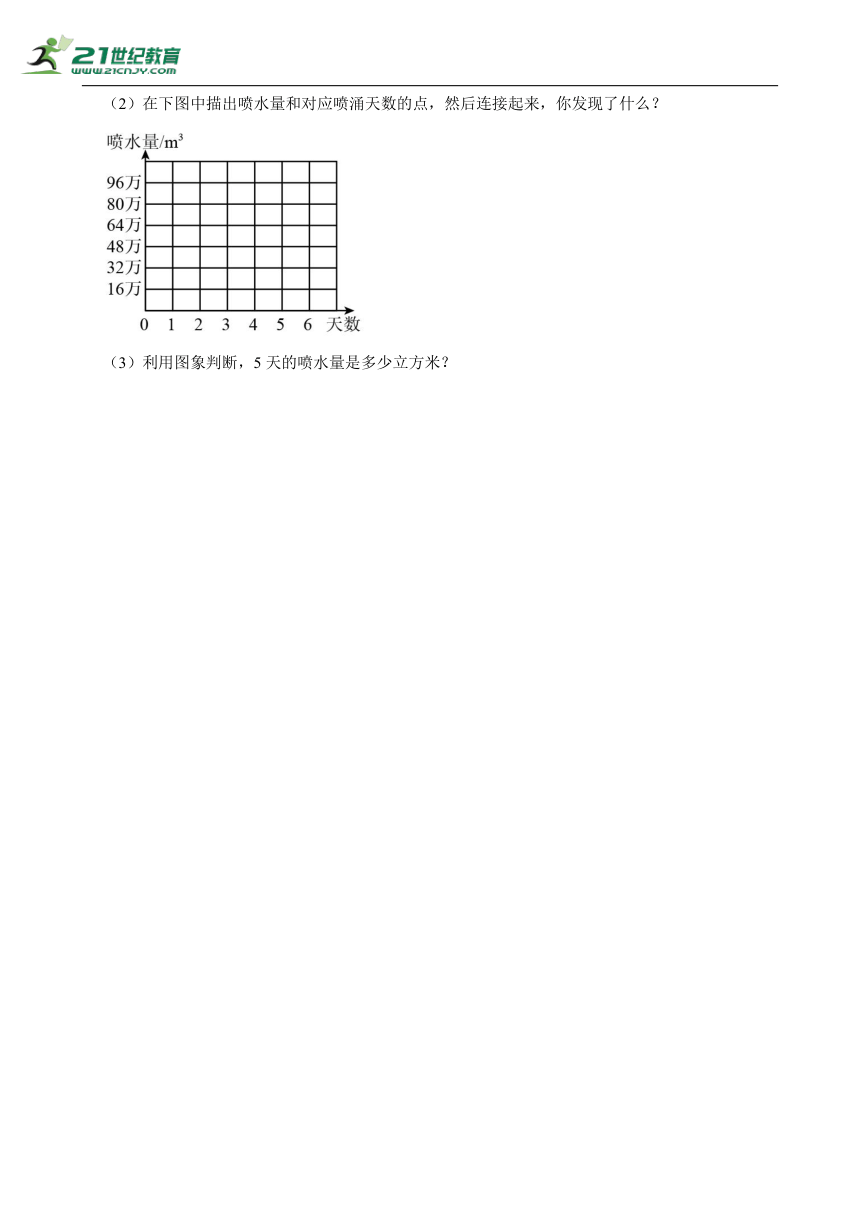
文档简介
4.2 正比例(同步练习)
一、单选题
1.用四根木条制作一个长方形框架,双手将它的两个对角慢慢向两边拉动,在这个变化的过程中,平行四边形的面积和高( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
2.成语“立竿见影”是指在阳光下竖起竹竿,立刻就能看到竹竿的影子。在同一时间,同一地点,竹竿的影长和竿高( )的关系。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.x和y成正比例关系,当x=2时,y=;当x=5时,y=( )。
A. B. C.2 D.
4.圆锥的高一定时,圆锥的体积和底面积( )。
A.成正比例 B.成反比例 C.不成比例 D.不能确定
5.在圆周长公式C=πd中,如果C一定,那么π与d( )。
A.成反比例 B.不成比例 C.成正比例
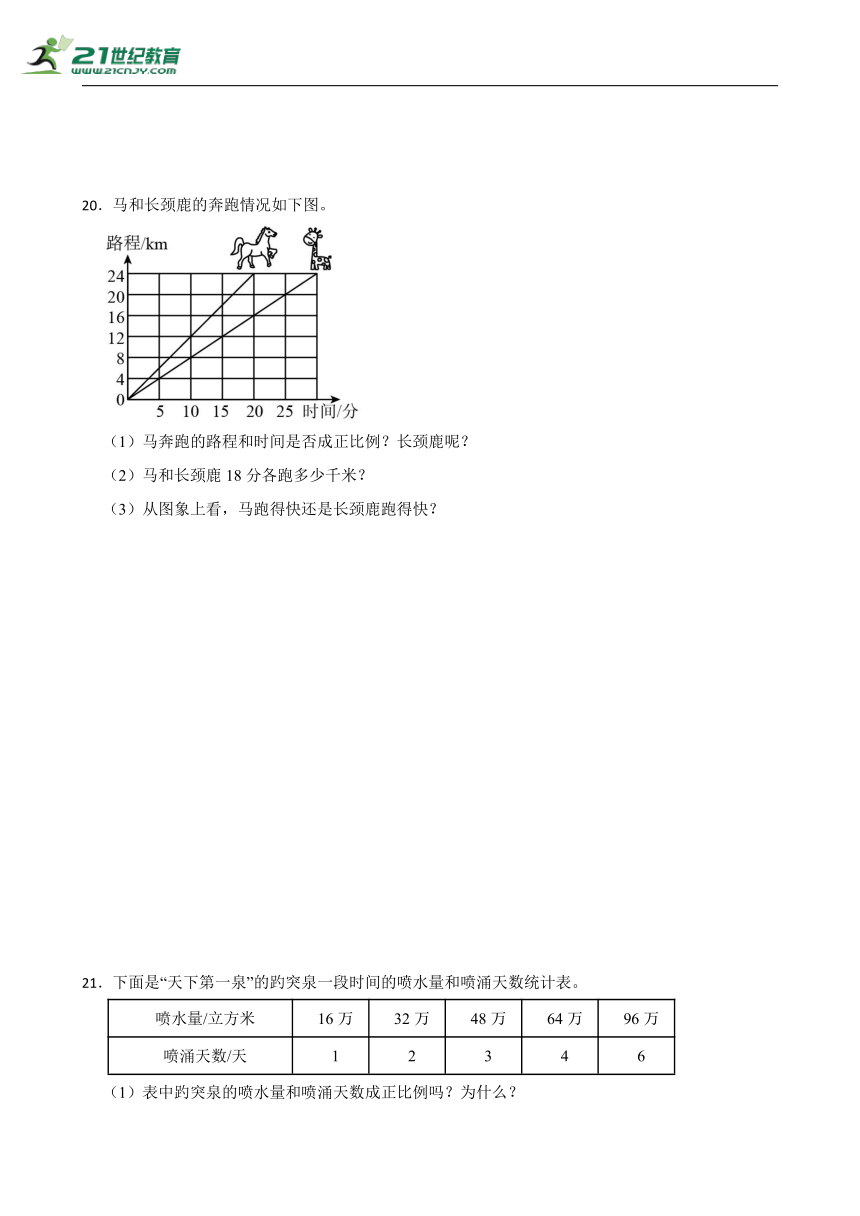
6.下图表示斑马和长颈鹿的奔跑情况,下面说法不符合这个图象的是( )。
A.斑马跑12千米用了10分钟
B.长颈鹿奔跑的路程与时间成正比例
C.照这样的速度长颈鹿跑40千米需50分钟
D.斑马比长颈鹿跑得慢
二、判断题
7.一个人个子越高体重越重,所以人的身高和体重成正比例关系。( )
8.已知a,b是两个相关联的量,若(a,b均不为0),则a与b成正比例。( )
9.同学们订阅了《少年月刊》,所订的份数和所需的总钱数成正比例。( )
10.一辆汽车的载重量一定,运送货物的总重量和运的次数成正比例。( )
三、填空题
11.圆的周长和它的直径成 比例;三角形的面积是8cm2,它的底和高成 比例。
12.报纸的单价一定,订阅的数量和总价成 比例关系;三角形的面积一定,它的底和高成 比例关系。
13.如果x=,那么x与y成 比例关系。如果4x=5y(x、y均不为0),那么x与y成 比例关系。
14.如果5a-7b=0(a、b均不为0),则a与b成 比例关系;圆柱的体积一定,它的底面积和高成 比例关系。
15.在比例尺一定的情况下,图上距离和实际距离成 比例。一根铁丝总长度一定,用去的长度和剩下的长度 比例。
16.每千克草莓的价钱一定,购买草莓的质量和总价成 比例。总收入一定,每小时劳动报酬与工作时间成 比例。
17.一个人的年龄越大,知识越渊博,所以年龄和知识成正比例。( )
四、操作题
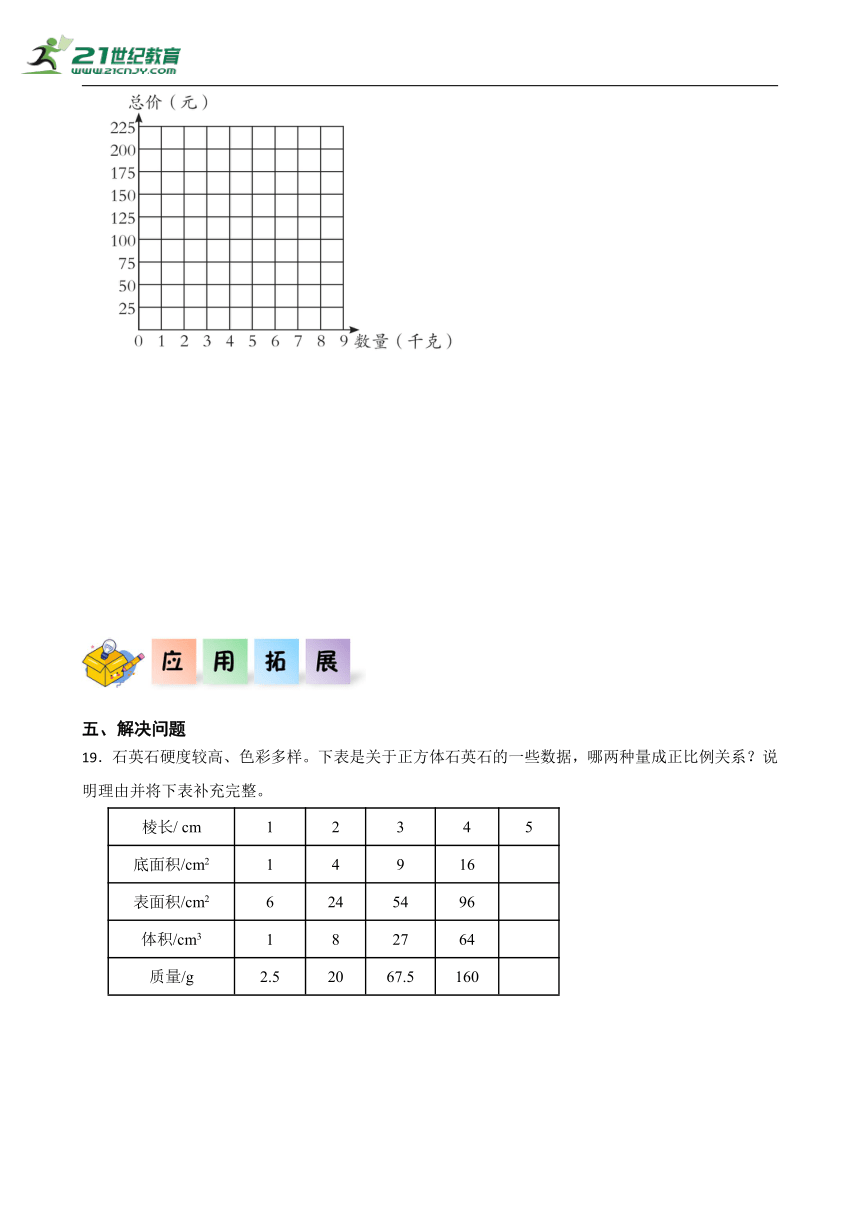
18.一种大樱桃销售数量与总价的关系如下:
数量(千克) 0 1 2 3 4 5 6 7 ……
总价(元) 0 25 50 75 100 125 150 175 ……
(1)数量与总价这两种量成什么比例关系?为什么?
(2)在图中描出数量和总价相对应的点,然后将它们连起来。
五、解决问题
19.石英石硬度较高、色彩多样。下表是关于正方体石英石的一些数据,哪两种量成正比例关系?说明理由并将下表补充完整。
棱长/ cm 1 2 3 4 5
底面积/cm2 1 4 9 16
表面积/cm2 6 24 54 96
体积/cm3 1 8 27 64
质量/g 2.5 20 67.5 160
20.马和长颈鹿的奔跑情况如下图。
(1)马奔跑的路程和时间是否成正比例?长颈鹿呢?
(2)马和长颈鹿18分各跑多少千米?
(3)从图象上看,马跑得快还是长颈鹿跑得快?
21.下面是“天下第一泉”的趵突泉一段时间的喷水量和喷涌天数统计表。
喷水量/立方米 16万 32万 48万 64万 96万
喷涌天数/天 1 2 3 4 6
(1)表中趵突泉的喷水量和喷涌天数成正比例吗?为什么?
(2)在下图中描出喷水量和对应喷涌天数的点,然后连接起来,你发现了什么?
(3)利用图象判断,5天的喷水量是多少立方米?
答案解析部分
1.A
解:平行四边形底=面积÷高,底不变,面积和高成正比例;
故答案为:A。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
2.A
解:竹竿的影长越长,竿就越高;
故答案为:A。
由题知,竹竿的影长随着竹竿变高而变长,且竹竿的影长和竿高的比值一定,根据“ 成正比例关系 是指两种相关联的量,一种量变化时,另一种量也随着变化,且这两种量中相对应的两个数的比值(或商)一定”判断得出竹竿的影长和竿高成正比例关系。
3.D
解:x和y成正比例关系,说明x和y的比值相等;
2:=5:y
2y=×5
2y=
y=×
y=
故答案为:D。
正比例的判断方法:相关联,能变化,商一定。
4.A
解:圆锥的体积与底面积是两种相关联的量,它们与圆锥的高有下面的关系:
圆锥的体积:底面积=圆锥的高(一定);已知圆锥的高一定,它的也是一定的,也就是圆锥的体积与底面积的比值一定,所以圆锥的体积与底面积成正比例。
故答案为:A。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
5.B
解:π是定量,C一定时,两个定量,一个变量,不符合比例关系概念,π与d不成比例。
故答案为:B。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
6.D
解:A项:斑马跑12千米用了10分钟,原题干说法正确;
B项:路程÷时间=速度(一定)长颈鹿奔跑的路程与时间成正比例,原题干说法正确;
C项:40÷(12÷15)
=40÷0.8
=50(分钟),原题干说法正确;
D项:斑马比长颈鹿跑得快,原题干说法错误。
故答案为:D。
A项:观察图像斑马跑12千米用了10分钟;
B项:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;
C项:照这样的速度长颈鹿跑40千米需要的时间=路程÷速度;
D项:时间相等,斑马跑的路程多,则斑马比长颈鹿跑得快。
7.错误
解:根据生活常识可知,一个人个子越高体重越重,但是身高和体重的乘积不一定,比值也不一定,所以它们不成比例;
故答案为:错误。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
8.错误
解:由,得ab=1.5,乘积一定,成反比例关系;原题说法错误。
故答案为:错误。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
9.正确
解:根据总价÷数量=单价,可知所需的总钱数÷所订的份数=每份《少年月刊》的钱数(一定),单价一定,则所订的份数和所需的总钱数成正比例。原题干说法正确。
故答案为:正确。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
10.正确
解:运货的次数与运货的总量是两种相关联的量,运货的总量随运货的次数的变化而变化,汽车的载重量一定,也就是运货的总量与运货的次数的比值一定,所以运货的总量与运货的次数是成正比例。
故答案为:正确。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
11.正;反
解:圆的周长÷直径=π,π是个定值,圆的周长和它的直径成正比;
三角形的面积=底×高,面积为8cm2,是个定值,底和高成反比;
故答案为:正,反。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
12.正;反
解:报纸的单价=总价÷订阅的数量,报纸的单价一定,订阅的数量和总价成正比;
三角形面积=底×高,三角形的面积一定,底和高成反比;
故答案为:正,反。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
13.反;正
解:→xy=4,x与y的乘积一定,x与y成反比例关系;
4x=5y→x:y=5:4,x与y的比值一定,x与y成正比例;
故答案为:反,正。
比例的基本性质:在比例中,两内项积等于两外项积;
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
14.正;反
解:5a-7b=0→5a=7b→a:b=7:5,a与b的比值一定,a与b成正比;
圆柱体积=底面积×高,圆柱的体积一定,底面积和高成反比;
故答案为:正,反。
比例的基本性质:在比例中,两内项积等于两外项积;
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
15.正;不成
解:图上距离:实际距离=比例尺,比例尺一定,图上距离和实际距离成正比例;
用去的长度+剩下的长度=铁丝总长度,铁丝总长度一定,用去的长度和剩下的长度不成比例;
故答案为:正,不成。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
16.正;反
解:总价÷购买草莓的质量=每千克草莓的价钱,每千克草莓的价钱一定,购买草莓的质量和总价成正比例;
每小时劳动报酬×工作时间=总收入,总收入一定,每小时劳动报酬与工作时间成反比例;
故答案为:正,反。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
17.错误
解:年龄和知识不是相关联的变量,不成比例,原题错误。
故答案为:错误。
如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;据此判断。
18.(1)解:成正比例关系,因为它们的比值一定。
(2)解:
(1)当两个量的比值相等时,这两个量成正比例关系;
(2)根据表格中的数据作图即可。
19.表面积与底面积成正比例关系,因为表面积与底面积是两种相关联的量,且表面积÷底面积=6(定值);质量与体积成正比例关系,因为质量与体积是两种相关联的量,且质量÷体积=2.5(定值)。
棱长/ cm 1 2 3 4 5
底面积/cm2 1 4 9 16 25
表面积/cm2 6 24 54 96 150
体积/cm3 1 8 27 64 125
质量/g 2.5 20 67.5 160 312.5
20.(1)解:12∶10=24∶20=1.2
8∶10=16∶20=0.8
答:马奔跑的路程和时间成正比例,长颈鹿奔跑的路程和时间成正比例。
(2)解:18×1.2=21.6(千米)
18×0.8=14.4(千米)
答:马和长颈鹿18分各跑21.6千米和14.4千米。
(3)解:从图象上看,马跑得快。
(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;马奔跑的路程和时间成正比例,长颈鹿奔跑的路程和时间成正比例;
(2)马和长颈鹿18分各跑的路程=分别的速度×奔跑的时间;
(3)从图象上看,时间相等,马跑得快。
21.(1)解:16∶1=32∶2=48∶3=64∶4=96∶6=16
答:表中趵突泉的喷水量和喷涌天数成正比例。因为喷水量和喷涌天数的比值是一定的。
(2)解:
我发现正比例的图像是一条直线。
(3)解:16×5=80(立方米)
答:5天的喷水量是80万立方米。
(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;表中趵突泉的喷水量和喷涌天数成正比例。因为喷水量和喷涌天数的比值是一定的;
(2)成正比例的图像是一条直线;
(3)5天的喷水量=平均每天的喷水量×天数。
一、单选题
1.用四根木条制作一个长方形框架,双手将它的两个对角慢慢向两边拉动,在这个变化的过程中,平行四边形的面积和高( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
2.成语“立竿见影”是指在阳光下竖起竹竿,立刻就能看到竹竿的影子。在同一时间,同一地点,竹竿的影长和竿高( )的关系。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.x和y成正比例关系,当x=2时,y=;当x=5时,y=( )。
A. B. C.2 D.
4.圆锥的高一定时,圆锥的体积和底面积( )。
A.成正比例 B.成反比例 C.不成比例 D.不能确定
5.在圆周长公式C=πd中,如果C一定,那么π与d( )。
A.成反比例 B.不成比例 C.成正比例
6.下图表示斑马和长颈鹿的奔跑情况,下面说法不符合这个图象的是( )。
A.斑马跑12千米用了10分钟
B.长颈鹿奔跑的路程与时间成正比例
C.照这样的速度长颈鹿跑40千米需50分钟
D.斑马比长颈鹿跑得慢
二、判断题
7.一个人个子越高体重越重,所以人的身高和体重成正比例关系。( )
8.已知a,b是两个相关联的量,若(a,b均不为0),则a与b成正比例。( )
9.同学们订阅了《少年月刊》,所订的份数和所需的总钱数成正比例。( )
10.一辆汽车的载重量一定,运送货物的总重量和运的次数成正比例。( )
三、填空题
11.圆的周长和它的直径成 比例;三角形的面积是8cm2,它的底和高成 比例。
12.报纸的单价一定,订阅的数量和总价成 比例关系;三角形的面积一定,它的底和高成 比例关系。
13.如果x=,那么x与y成 比例关系。如果4x=5y(x、y均不为0),那么x与y成 比例关系。
14.如果5a-7b=0(a、b均不为0),则a与b成 比例关系;圆柱的体积一定,它的底面积和高成 比例关系。
15.在比例尺一定的情况下,图上距离和实际距离成 比例。一根铁丝总长度一定,用去的长度和剩下的长度 比例。
16.每千克草莓的价钱一定,购买草莓的质量和总价成 比例。总收入一定,每小时劳动报酬与工作时间成 比例。
17.一个人的年龄越大,知识越渊博,所以年龄和知识成正比例。( )
四、操作题
18.一种大樱桃销售数量与总价的关系如下:
数量(千克) 0 1 2 3 4 5 6 7 ……
总价(元) 0 25 50 75 100 125 150 175 ……
(1)数量与总价这两种量成什么比例关系?为什么?
(2)在图中描出数量和总价相对应的点,然后将它们连起来。
五、解决问题
19.石英石硬度较高、色彩多样。下表是关于正方体石英石的一些数据,哪两种量成正比例关系?说明理由并将下表补充完整。
棱长/ cm 1 2 3 4 5
底面积/cm2 1 4 9 16
表面积/cm2 6 24 54 96
体积/cm3 1 8 27 64
质量/g 2.5 20 67.5 160
20.马和长颈鹿的奔跑情况如下图。
(1)马奔跑的路程和时间是否成正比例?长颈鹿呢?
(2)马和长颈鹿18分各跑多少千米?
(3)从图象上看,马跑得快还是长颈鹿跑得快?
21.下面是“天下第一泉”的趵突泉一段时间的喷水量和喷涌天数统计表。
喷水量/立方米 16万 32万 48万 64万 96万
喷涌天数/天 1 2 3 4 6
(1)表中趵突泉的喷水量和喷涌天数成正比例吗?为什么?
(2)在下图中描出喷水量和对应喷涌天数的点,然后连接起来,你发现了什么?
(3)利用图象判断,5天的喷水量是多少立方米?
答案解析部分
1.A
解:平行四边形底=面积÷高,底不变,面积和高成正比例;
故答案为:A。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
2.A
解:竹竿的影长越长,竿就越高;
故答案为:A。
由题知,竹竿的影长随着竹竿变高而变长,且竹竿的影长和竿高的比值一定,根据“ 成正比例关系 是指两种相关联的量,一种量变化时,另一种量也随着变化,且这两种量中相对应的两个数的比值(或商)一定”判断得出竹竿的影长和竿高成正比例关系。
3.D
解:x和y成正比例关系,说明x和y的比值相等;
2:=5:y
2y=×5
2y=
y=×
y=
故答案为:D。
正比例的判断方法:相关联,能变化,商一定。
4.A
解:圆锥的体积与底面积是两种相关联的量,它们与圆锥的高有下面的关系:
圆锥的体积:底面积=圆锥的高(一定);已知圆锥的高一定,它的也是一定的,也就是圆锥的体积与底面积的比值一定,所以圆锥的体积与底面积成正比例。
故答案为:A。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
5.B
解:π是定量,C一定时,两个定量,一个变量,不符合比例关系概念,π与d不成比例。
故答案为:B。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系;
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
6.D
解:A项:斑马跑12千米用了10分钟,原题干说法正确;
B项:路程÷时间=速度(一定)长颈鹿奔跑的路程与时间成正比例,原题干说法正确;
C项:40÷(12÷15)
=40÷0.8
=50(分钟),原题干说法正确;
D项:斑马比长颈鹿跑得快,原题干说法错误。
故答案为:D。
A项:观察图像斑马跑12千米用了10分钟;
B项:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;
C项:照这样的速度长颈鹿跑40千米需要的时间=路程÷速度;
D项:时间相等,斑马跑的路程多,则斑马比长颈鹿跑得快。
7.错误
解:根据生活常识可知,一个人个子越高体重越重,但是身高和体重的乘积不一定,比值也不一定,所以它们不成比例;
故答案为:错误。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
8.错误
解:由,得ab=1.5,乘积一定,成反比例关系;原题说法错误。
故答案为:错误。
由正、反比例的意义可知:如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;如果两种相关联的量的商一定,那么这两种时就成正比例关系,据此作答。
9.正确
解:根据总价÷数量=单价,可知所需的总钱数÷所订的份数=每份《少年月刊》的钱数(一定),单价一定,则所订的份数和所需的总钱数成正比例。原题干说法正确。
故答案为:正确。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
10.正确
解:运货的次数与运货的总量是两种相关联的量,运货的总量随运货的次数的变化而变化,汽车的载重量一定,也就是运货的总量与运货的次数的比值一定,所以运货的总量与运货的次数是成正比例。
故答案为:正确。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
11.正;反
解:圆的周长÷直径=π,π是个定值,圆的周长和它的直径成正比;
三角形的面积=底×高,面积为8cm2,是个定值,底和高成反比;
故答案为:正,反。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
12.正;反
解:报纸的单价=总价÷订阅的数量,报纸的单价一定,订阅的数量和总价成正比;
三角形面积=底×高,三角形的面积一定,底和高成反比;
故答案为:正,反。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
13.反;正
解:→xy=4,x与y的乘积一定,x与y成反比例关系;
4x=5y→x:y=5:4,x与y的比值一定,x与y成正比例;
故答案为:反,正。
比例的基本性质:在比例中,两内项积等于两外项积;
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
14.正;反
解:5a-7b=0→5a=7b→a:b=7:5,a与b的比值一定,a与b成正比;
圆柱体积=底面积×高,圆柱的体积一定,底面积和高成反比;
故答案为:正,反。
比例的基本性质:在比例中,两内项积等于两外项积;
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
15.正;不成
解:图上距离:实际距离=比例尺,比例尺一定,图上距离和实际距离成正比例;
用去的长度+剩下的长度=铁丝总长度,铁丝总长度一定,用去的长度和剩下的长度不成比例;
故答案为:正,不成。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
16.正;反
解:总价÷购买草莓的质量=每千克草莓的价钱,每千克草莓的价钱一定,购买草莓的质量和总价成正比例;
每小时劳动报酬×工作时间=总收入,总收入一定,每小时劳动报酬与工作时间成反比例;
故答案为:正,反。
判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
17.错误
解:年龄和知识不是相关联的变量,不成比例,原题错误。
故答案为:错误。
如果两种相关联的量的乘积一定,那么这两种时就成反比例关系;据此判断。
18.(1)解:成正比例关系,因为它们的比值一定。
(2)解:
(1)当两个量的比值相等时,这两个量成正比例关系;
(2)根据表格中的数据作图即可。
19.表面积与底面积成正比例关系,因为表面积与底面积是两种相关联的量,且表面积÷底面积=6(定值);质量与体积成正比例关系,因为质量与体积是两种相关联的量,且质量÷体积=2.5(定值)。
棱长/ cm 1 2 3 4 5
底面积/cm2 1 4 9 16 25
表面积/cm2 6 24 54 96 150
体积/cm3 1 8 27 64 125
质量/g 2.5 20 67.5 160 312.5
20.(1)解:12∶10=24∶20=1.2
8∶10=16∶20=0.8
答:马奔跑的路程和时间成正比例,长颈鹿奔跑的路程和时间成正比例。
(2)解:18×1.2=21.6(千米)
18×0.8=14.4(千米)
答:马和长颈鹿18分各跑21.6千米和14.4千米。
(3)解:从图象上看,马跑得快。
(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;马奔跑的路程和时间成正比例,长颈鹿奔跑的路程和时间成正比例;
(2)马和长颈鹿18分各跑的路程=分别的速度×奔跑的时间;
(3)从图象上看,时间相等,马跑得快。
21.(1)解:16∶1=32∶2=48∶3=64∶4=96∶6=16
答:表中趵突泉的喷水量和喷涌天数成正比例。因为喷水量和喷涌天数的比值是一定的。
(2)解:
我发现正比例的图像是一条直线。
(3)解:16×5=80(立方米)
答:5天的喷水量是80万立方米。
(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量;表中趵突泉的喷水量和喷涌天数成正比例。因为喷水量和喷涌天数的比值是一定的;
(2)成正比例的图像是一条直线;
(3)5天的喷水量=平均每天的喷水量×天数。
