哈尔滨市道里区2014-2015学年八年级下期末数学试卷含答案解析
文档属性
| 名称 | 哈尔滨市道里区2014-2015学年八年级下期末数学试卷含答案解析 |  | |
| 格式 | zip | ||
| 文件大小 | 191.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-15 13:27:45 | ||
图片预览



文档简介
2014-2015学年黑龙江省哈尔滨市道里区八年级(下)期末数学试卷
一、选择题
1.下列图形不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
2.下列方程,是一元二次方程的是( )
A.2(x﹣1)=3x B. C.2x2﹣x=0 D.x(x﹣1)=y
3.下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
4. ABCD的周长为40 cm,△ABC的周长为25 cm,则对角线AC长为( )
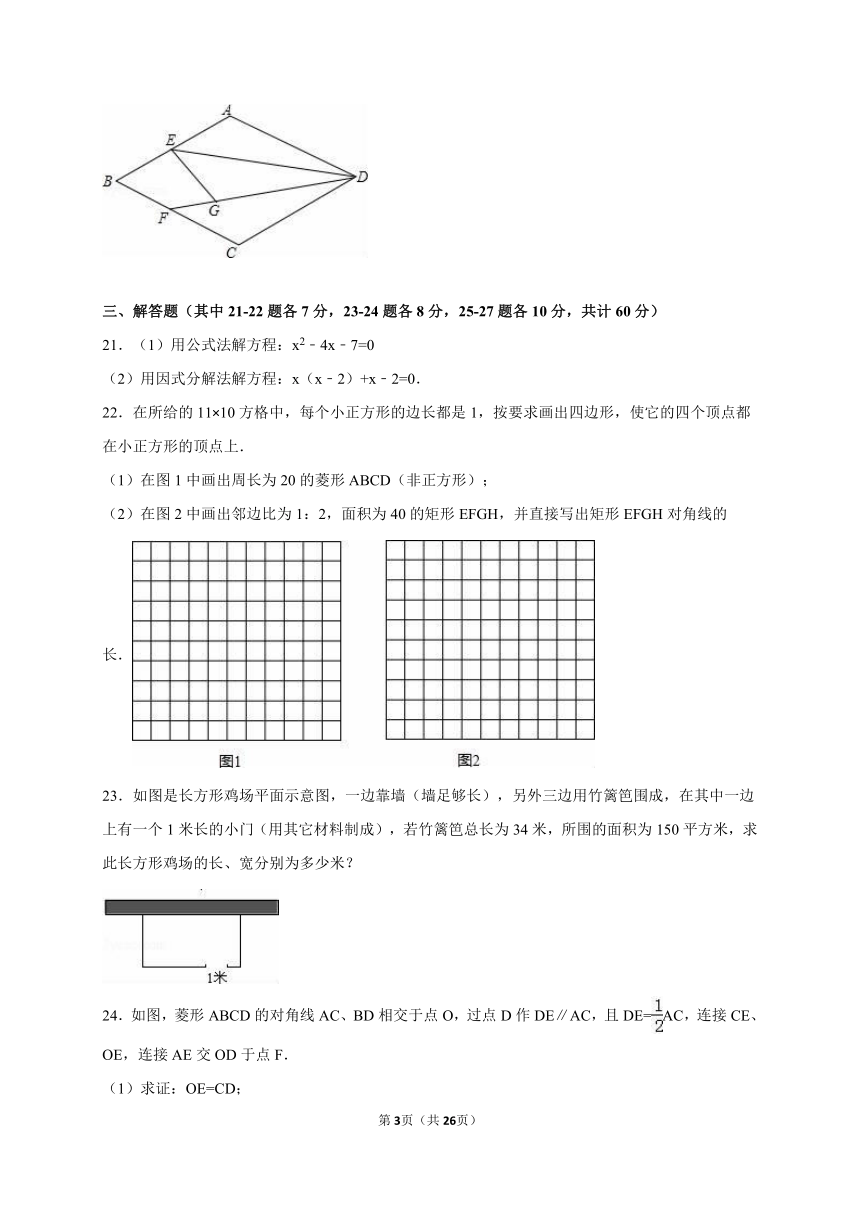
A.5cm B.15cm C.6cm D.16cm
5.下列命题的逆命题正确的是( )
A.如果两个角是直角,那么它们相等
B.全等三角形的面积相等
C.同位角相等,两直线平行
D.若a=b,则a2=b2
6.顺次连接对角线相等的四边形各边中点,所得到的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
7.点A(﹣5,y1)和B(﹣2,y2)都在直线y=﹣3x上,则y1与y2的关系是( )
A.y1≤y2 B.y1=y2 C.y1<y2 D.y1>y2
8.将直线y=3x﹣2平移后,得到直线y=3x+6,则原直线( )
A.沿y轴向上平移了8个单位 B.沿y轴向下平移了8个单位
C.沿x轴向左平移了8个单位 D.沿x轴向右平移了8个单位
9.等腰三角形的底和腰是方程x2﹣6x+8=0的两根,则这个三角形的周长为( )
A.8 B.10 C.8或10 D.不能确定
10.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:
①起跑后1小时内,甲在乙的前面;
②第1小时两人都跑了10千米;
③甲比乙先到达终点;
④两人都跑了20千米.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.在函数y=中,自变量x的取值范围是 .
12.函数y=3x+b(b<0)的图象不经过第 象限.
13.三角形三条中位线围成的三角形的周长为6,则它的周长是 .
14.已知一元二次方程x2+px+3=0的一个根为﹣3,则p= .
15.两直角边分别为12和16的直角三角形斜边上的中线的长是 .
16.已知菱形两条对角线的长分别为4cm和8cm,则这个菱形的面积是 ,周长是 .
17.如果一次函数y=﹣2x+b的图象交x轴于点(﹣3,0),那么关于x的不等式﹣2x+b<0的解集为 .
18.已知关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则实数k的取值范围是 .
19.已知矩形ABCD中,BE平分∠ABC交矩形的一条边于点E,若BD=10,∠EBD=15°,则AB= .
20.如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF= .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(1)用公式法解方程:x2﹣4x﹣7=0
(2)用因式分解法解方程:x(x﹣2)+x﹣2=0.
22.在所给的11×10方格中,每个小正方形的边长都是1,按要求画出四边形,使它的四个顶点都在小正方形的顶点上.
(1)在图1中画出周长为20的菱形ABCD(非正方形);
(2)在图2中画出邻边比为1:2,面积为40的矩形EFGH,并直接写出矩形EFGH对角线的长.
23.如图是长方形鸡场平面示意图,一边靠墙(墙足够长),另外三边用竹篱笆围成,在其中一边上有一个1米长的小门(用其它材料制成),若竹篱笆总长为34米,所围的面积为150平方米,求此长方形鸡场的长、宽分别为多少米?
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
25.某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.并求怎样购买使费用最少,最少费用是多少元?
26.如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1)求证:AF﹣BF=EF;
(2)若AG=,EF=1,求四边形DEGC的面积.
27.如图,平面直角坐标系中,矩形OABC,B(5,4),将矩形沿过点C的直线翻折,使点B落在线段OA上的点D处,折痕交AB于点E,P(m,0)是射线OA上一动点过点P作x轴的垂线,分别交直线CE和直线CB于点Q和点R.
(1)求点E的坐标;
(2)在点P的运动过程中,求的值;
(3)设直线CE交x轴于点F,过点P作x轴的垂线交直线CD于点K,连接KE,当∠CKE=∠CFO时,求出m的值和线段CQ的长.
2014-2015学年黑龙江省哈尔滨市道里区八年级(下)期末数学试卷
参考答案与试题解析
一、选择题
1.下列图形不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
【考点】轴对称图形.
【分析】根据轴对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
【解答】解:A、不是轴对称图形,故选项正确;
B、是轴对称图形,故选项错误;
C、是轴对称图形,故选项错误;
D、是轴对称图形,故选项错误.
故选A.
【点评】掌握好轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.下列方程,是一元二次方程的是( )
A.2(x﹣1)=3x B. C.2x2﹣x=0 D.x(x﹣1)=y
【考点】一元二次方程的定义.
【专题】常规题型.
【分析】本题根据一元二次方程的定义解答.一元二次方程必须满足四个条件:(1)未知数的最高次数是2;(2)二次项系数不为0;
(3)是整式方程;(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
【解答】解:A、方程二次项系数为0,故本选项错误;
B、不是整式方程,故本选项错误;
C、符合一元二次方程的定义,故本选项正确;
D、有两个未知数,故本选项错误.
故选C.
【点评】本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.
3.下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
【考点】勾股定理的逆定理.
【专题】计算题.
【分析】判断是否为直角三角形,只要验证两小边的平方和等于最长边的平方即可.
【解答】解:A、22+32=13≠42,故A选项构成不是直角三角形;
B、32+42=25≠62,故B选项构成不是直角三角形;
C、52+122=169=132,故C选项构成是直角三角形;
D、42+62=52≠72,故D选项构成不是直角三角形.
故选:C.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
4. ABCD的周长为40 cm,△ABC的周长为25 cm,则对角线AC长为( )
A.5cm B.15cm C.6cm D.16cm
【考点】平行四边形的性质.
【分析】由 ABCD的周长为40 cm,可得AB+BC=20cm,又有△ABC的周长为25 cm,即可求对角线AC长.
【解答】解:∵ ABCD的周长为40 cm,
∴AB+BC=20cm,
又∵△ABC的周长为25 cm,
∴对角线AC长为25﹣20=5cm.
故选A.
【点评】此题主要考查平行四边的性质:平行四边形的两组对边分别相等.
5.下列命题的逆命题正确的是( )
A.如果两个角是直角,那么它们相等
B.全等三角形的面积相等
C.同位角相等,两直线平行
D.若a=b,则a2=b2
【考点】命题与定理.
【分析】交换原命题的题设与结论得到四个命题的逆命题,然后分别根据直角的定义、全等三角形的判定、平行线的性质和平方根的定义判定四个逆命题的真假.
【解答】解:A、逆命题为:如果两个角相等,那么它们都是直角,此逆命题为假命题;
B、逆命题为:面积相等的两三角形全等,此逆命题为假命题;
C、逆命题为:两直线平行,同位角相等,此逆命题为真命题;
D、逆命题为,若a2=b2,则a=b,此逆命题为假命题.
故选C.
【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆命题.
6.顺次连接对角线相等的四边形各边中点,所得到的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
【考点】三角形中位线定理;菱形的判定.
【分析】首先根据三角形的中位线定理,得新四边形各边都等于原四边形的对角线的一半;
再结合原四边形的对角线相等,从而得到新四边形各边相等,根据菱形的判定方法知新四边形即为菱形.
【解答】解:根据三角形的中位线定理,得
新四边形各边都等于原四边形的对角线的一半.
又∵原四边形的对角线相等,
∴新四边形各边相等,
根据四边相等的四边形是菱形,得新四边形为菱形.
故选B.
【点评】本题主要考查了三角形的中位线定理和菱形的判定方法.
7.点A(﹣5,y1)和B(﹣2,y2)都在直线y=﹣3x上,则y1与y2的关系是( )
A.y1≤y2 B.y1=y2 C.y1<y2 D.y1>y2
【考点】一次函数图象上点的坐标特征.
【分析】根据一次函数的性质即可作出判断.
【解答】解:∵一次函数中一次项系数﹣3<0,﹣5<﹣2,
∴y1>y2.
故选D
【点评】本题考查了一次函数的性质,在解析式y=kx+b(k≠0,且k,b是常数)中,当k<0时,y随x的增大而减小.
8.将直线y=3x﹣2平移后,得到直线y=3x+6,则原直线( )
A.沿y轴向上平移了8个单位 B.沿y轴向下平移了8个单位
C.沿x轴向左平移了8个单位 D.沿x轴向右平移了8个单位
【考点】一次函数图象与几何变换.
【分析】利用一次函数图象的平移规律,左加右减,上加下减,得出即可.
【解答】解:∵将直线y=3x﹣2平移后,得到直线y=3x+6,
∴3x﹣2+a=3x+6,
解得:a=8,
所以沿y轴向上平移了8个单位,
故选A
【点评】此题主要考查了一次函数图象与几何变换,正确把握变换规律是解题关键.
9.等腰三角形的底和腰是方程x2﹣6x+8=0的两根,则这个三角形的周长为( )
A.8 B.10 C.8或10 D.不能确定
【考点】等腰三角形的性质;解一元二次方程-因式分解法;三角形三边关系.
【专题】计算题.
【分析】先求出方程的根,再根据三角形三边关系确定是否符合题意,然后求解.
【解答】解:∵方程x2﹣6x+8=0的解是x=2或4,
(1)当2为腰,4为底时,2+2=4不能构成三角形;
(2)当4为腰,2为底时,4,4,2能构成等腰三角形,周长=4+4+2=10.
故选:B.
【点评】本题考查了等腰三角形的性质和分情况讨论的思想,注意根据三角形的三边关系确定是否能构成三角形,不可盲目讨论.
10.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:
①起跑后1小时内,甲在乙的前面;
②第1小时两人都跑了10千米;
③甲比乙先到达终点;
④两人都跑了20千米.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
【考点】函数的图象.
【专题】压轴题.
【分析】由图象可知起跑后1小时内,甲在乙的前面;在跑了1小时时,乙追上甲,此时都跑了10千米;乙比甲先到达终点;求得乙跑的直线的解析式,即可求得两人跑的距离,则可求得答案.
【解答】解:根据图象得:
起跑后1小时内,甲在乙的前面;故①正确;
在跑了1小时时,乙追上甲,此时都跑了10千米,故②正确;
乙比甲先到达终点,故③错误;
设乙跑的直线解析式为:y=kx,
将点(1,10)代入得:k=10,
∴解析式为:y=10x,
∴当x=2时,y=20,
∴两人都跑了20千米,故④正确.
所以①②④三项正确.
故选:C.
【点评】此题考查了函数图形的意义.解题的关键是根据题意理解各段函数图象的实际意义,正确理解函数图象横纵坐标表示的意义,理解问题的过程.
二、填空题
11.在函数y=中,自变量x的取值范围是 x≠﹣ .
【考点】函数自变量的取值范围.
【分析】根据分母不等于0列式计算即可得解.
【解答】解:由题意得,3x+2≠0,
解得x≠﹣.
故答案为:x≠﹣.
【点评】本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
12.函数y=3x+b(b<0)的图象不经过第 二 象限.
【考点】一次函数图象与系数的关系.
【分析】根据一次函数的图象与系数的关系即可得出结论.
【解答】解:∵函数y=3x+b(b<0)中,k=3>0,b<0,
∴此函数的图象经过一、三、四象限,不经过第二象限.
故答案为:二.
【点评】本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k>0,b<0时函数的图象在一、三、四象限是解答此题的关键.
13.三角形三条中位线围成的三角形的周长为6,则它的周长是 12 .
【考点】三角形中位线定理.
【专题】计算题.
【分析】根据三角形的中位线定理知:三条中位线围成的三角形的各边是对应原三角形各边的一半,所以原三角形的周长是12.
【解答】解:根据题意可知,原三角形的周长=2×6=12.
故答案为:12.
【点评】本题考查了三角形中位线定理的数量关系:三角形的中位线等于第三边的一半.
14.已知一元二次方程x2+px+3=0的一个根为﹣3,则p= 4 .
【考点】一元二次方程的解.
【分析】已知一元二次方程x2+px+3=0的一个根为﹣3,因而把x=﹣3代入方程即可求得p的值.
【解答】解:把x=﹣3代入方程可得:(﹣3)2﹣3p+3=0,
解得p=4
故填:4.
【点评】本题主要考查了方程的解的定义,把求未知系数的问题转化为方程求解的问题.
15.两直角边分别为12和16的直角三角形斜边上的中线的长是 10 .
【考点】直角三角形斜边上的中线;勾股定理.
【分析】根据勾股定理求出斜边长,根据直角三角形斜边上的中线等于斜边的一半求出答案.
【解答】解:∵两直角边分别为12和16,
∴斜边==20,
∴斜边上的中线的长为10,
故答案为:10.
【点评】本题考查的是直角三角形的性质和勾股定理,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.
16.已知菱形两条对角线的长分别为4cm和8cm,则这个菱形的面积是 16 ,周长是 8 .
【考点】菱形的性质.
【分析】根据菱形的面积公式:两对角线乘积的一半,求得菱形的面积;再由菱形的两对角线的一半和勾股定理求得菱形的边长,进而求出周长.
【解答】解:菱形的面积=(4×8)÷2=18cm2.
菱形的边长==2,
∴周长=4×2=8.
故答案为:16,.
【点评】本题主要利用勾股定理求边长和菱形的面积公式:“对角线乘积的一半”来解决.
17.如果一次函数y=﹣2x+b的图象交x轴于点(﹣3,0),那么关于x的不等式﹣2x+b<0的解集为 x<﹣3 .
【考点】一次函数与一元一次不等式.
【分析】根据题意画出函数图象,利用数形结合即可得出结论.
【解答】解:如图所示,关于x的不等式﹣2x+b<0的解集为x<﹣3.
故答案为:x<﹣3.
【点评】本题考查的是一次函数与一元一次不等式,能利用数形结合求出不等式的取值范围是解答此题的关键.
18.已知关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则实数k的取值范围是 k>﹣1且k≠0. .
【考点】根的判别式.
【专题】计算题.
【分析】根据一元二次方程的定义以及根的判别式得到k≠0,且△>0,然后解两个不等式即可得到实数k的取值范围.
【解答】解:根据题意得,k≠0,且△>0,即22﹣4×k×(﹣1)>0,解得k>﹣1,
∴实数k的取值范围为k>﹣1且k≠0.
故答案为k>﹣1且k≠0.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根;也考查了一元二次方程的定义.
19.已知矩形ABCD中,BE平分∠ABC交矩形的一条边于点E,若BD=10,∠EBD=15°,则AB= 5或5 .
【考点】矩形的性质;含30度角的直角三角形.
【专题】分类讨论.
【分析】化成符合条件的两种情况,根据矩形性质求出∠A=∠ABC=∠C=90°,∠ABE=∠CBE=45°,求出∠DBC和∠ABD的度数,求出CD和AD,即可求出AB.
【解答】解:有两种情况:如图
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠C=90°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=45°,
图1中,∵∠EBD=15°,
∴∠DBC=30°,
∴CD=BD=5,
即AB=CD=5;
图2中,∵∠EBD=15°,
∴∠ABD=30°,
∴AD=BD=5,
在Rt△ABD中,由勾股定理得:AB==5.
故答案为:5或5.
【点评】本题考查了矩形性质和含30度角的直角三角形性质,勾股定理的应用,关键是化成符合条件的所有情况,题目比较典型,是一道比较好的题目.
20.如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF= .
【考点】菱形的性质;翻折变换(折叠问题).
【专题】计算题.
【分析】DE和CB的延长线相交于G'点,连结EF,作EH⊥DF于H点,如图,根据菱形的性质得A=180°﹣∠B=120°,AB=AD=2,AD∥BC,则∠1=∠G,再利用折叠的性质得∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,则∠4=60°,在Rt△EHG中利用含30度的直角三角形三边的关系得到HG=EG=,EH=EH=,则在Rt△DEH中利用勾股定理可计算出DE=,再证明∠2=∠G'得到FG'=FD,证明△AED≌△BEG'得到DE=G'E,所以FE⊥DG',然后证明Rt△DEF∽Rt△DHE,利用相似比计算出DF=,则FG=FD﹣DG=,于是得到BF=FG=.
【解答】解DE和CB的延长线相交于G’点,连结EF,作EH⊥DF于H点,如图,
∵四边形ABCD为菱形,
∴∠A=180°﹣∠B=120°,AB=AD=2,AD∥BC
∴∠1=∠G',
而E为AB的中点,
∴AE=BE=1,
∵△AED沿DE翻折得到△GED,
∴∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,
∴∠4=60°,
在Rt△EHG中,HG=EG=,EH=EH=,
在Rt△DEH中,DE===,
∵AD∥BG',
∴∠1=∠G',
∴∠G'=∠2,
∴FG=FD,
在△AED和△BEG'中,
,
∴△AED≌△BEG',
∴DE=G'E,
∴FE⊥DG',
∴∠FED=90°,
∵∠HDE=∠EDF,
∴Rt△DEF∽Rt△DHE,
∴=,即=,
∴DF=,
∴FG=FD﹣DG=﹣2=,
∴BF=FG=.
故答案为.
【点评】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了折叠的性质、全等三角形的判定与性质和相似三角形的判定与性质.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(1)用公式法解方程:x2﹣4x﹣7=0
(2)用因式分解法解方程:x(x﹣2)+x﹣2=0.
【考点】解一元二次方程-因式分解法;解一元二次方程-公式法.
【专题】计算题.
【分析】(1)方程利用公式法求出解即可;
(2)方程利用因式分解法求出解即可.
【解答】解:(1)这里a=1,b=﹣4,c=﹣7,
∵△=16+28=44,
∴x==2±;
(2)分解因式得:(x﹣2)(x+1)=0,
可得x﹣2=0或x+1=0,
解得:x1=2,x2=﹣1.
【点评】此题考查了解一元二次方程﹣因式分解法,熟练掌握因式分解的方法是解本题的关键.
22.在所给的11×10方格中,每个小正方形的边长都是1,按要求画出四边形,使它的四个顶点都在小正方形的顶点上.
(1)在图1中画出周长为20的菱形ABCD(非正方形);
(2)在图2中画出邻边比为1:2,面积为40的矩形EFGH,并直接写出矩形EFGH对角线的长.
【考点】作图—应用与设计作图;菱形的性质;矩形的性质.
【分析】(1)由菱形的周长为20,可得边长为5,即作直角边分别为3和4的直角三角形,则斜边为5,即可得到菱形ABCD;
(2)利用已知条件可求出矩形的长和宽,进而可画出矩形EFGH,利用勾股定理可求出其对角线的长.
【解答】解:(1)如图所示:
(2)∵矩形EFGH的面积=40,长:宽=2:1,
∴长=4,宽=2,
∴其对角线EG=FH==10,
如图所示:
【点评】此题主要考查了应用设计与作图以及勾股定理和菱形、矩形的性质,正确借助网格得出是解题关键.
23.如图是长方形鸡场平面示意图,一边靠墙(墙足够长),另外三边用竹篱笆围成,在其中一边上有一个1米长的小门(用其它材料制成),若竹篱笆总长为34米,所围的面积为150平方米,求此长方形鸡场的长、宽分别为多少米?
【考点】一元二次方程的应用.
【专题】几何图形问题.
【分析】设长方形鸡场的长为x米,则宽为(34+1﹣x)米,由此根据长方形的面积计算方法由所围的面积为150平方米,建立方程解决问题.
【解答】解:设长方形鸡场的长为x米,则宽为(34+1﹣x)米,由题意得
x (34+1﹣x)=150
解得:x1=15,x2=20
当x=15时,(34+1﹣x)=10,
当x=20时,(34+1﹣x)=7.5,
答:长方形鸡场的长为15米,宽为10米或长方形鸡场的长为20米,宽为7.5米.
【点评】此题考查一元二次方程的实际运用,掌握长方形的周长和面积计算公式是解决问题的前提.
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
【考点】菱形的性质;矩形的判定与性质.
【分析】(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,可得OE=CD即可;
(2)根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
【解答】(1)证明:在菱形ABCD中,OC=AC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=4.
∴在矩形OCED中,CE=OD==2.
在Rt△ACE中,
AE==2.
【点评】本题考查了菱形的性质,矩形的判定与性质,勾股定理的应用,是基础题,熟记矩形的判定方法与菱形的性质是解题的关键.
25.某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.并求怎样购买使费用最少,最少费用是多少元?
【考点】一次函数的应用;二元一次方程组的应用;一元一次不等式的应用.
【分析】(1)设A奖品的单价是x元,B奖品的单价是y元,根据条件建立方程组求出其解即可;
(2)根据总费用=两种奖品的费用之和表示出W与m的关系式,并有条件建立不等式组求出x的取值范围,由一次函数的性质就可以求出结论.
【解答】解(1)设A奖品的单价是x元,B奖品的单价是y元,由题意,得
,
解得:.
答:A奖品的单价是10元,B奖品的单价是15元;
(2)由题意,得
W=10m+15(100﹣m)=﹣5m+1500
∴m≤3(100﹣m),
解得:m≤75,
∵W=﹣5m+1500,
∴k=﹣5<0,
∴W随m的增大而减小,
∴m=75时,W最小=1125,
∴应买A种奖品75件,B种奖品25件,才能使总费用最少为1125元.
【点评】本题考查了一次函数的性质的运用,二元一次方程组的运用,一元一次不等式组的运用,解答时求一次函数的解析式是关键.
26.如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1)求证:AF﹣BF=EF;
(2)若AG=,EF=1,求四边形DEGC的面积.
【考点】正方形的性质;全等三角形的判定与性质.
【分析】(1)先利用等角的余角相等得到∠BAF=∠ADE,则可根据”AAS“判定△ABF≌△DAE,得到BF=AE,所以AF﹣BF=AF﹣AE=EF;
(2)设AE=BF=a,则AF=a+1,由(1)得△ABF≌△DAE,所以DE=AF=a+1,在Rt△ADE中利用勾股定理得到AD2=a2+(a+1)2,再证明Rt△ABF∽Rt△AGB,利用相似比得AB2=AF AG=(a+1)×,所以a2+(a+1)2=(a+1)×,整理得8a2﹣17a﹣21=0,解得a1=3,a2=﹣(舍去),即可得到AB=5,然后利用四边形DEGC的面积=S正方形ABCD﹣S△ABG﹣S△AED进行计算.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵E⊥AG于点E,BF⊥AG于点F,
∴∠AED=∠BFA=90°,
∴∠DAE+∠ADE=90°,
而∠DAE+∠BAF=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE,
∴BF=AE,
∴AF﹣BF=AF﹣AE=EF;
(2)解:设AE=BF=a,则AF=a+1,
∵△ABF≌△DAE,
∴DE=AF=a+1,
在Rt△ADE中,AD2=a2+(a+1)2,
∵∠BAF=∠GAB,
∴Rt△ABF∽Rt△AGB,
∴AB:AG=AF:AB,
∴AB2=AF AG=(a+1)×,
而AB=AD,
∴a2+(a+1)2=(a+1)×,
整理得8a2﹣17a﹣21=0,解得a1=3,a2=﹣(舍去),
∴AB==5,
∴四边形DEGC的面积=S正方形ABCD﹣S△ABG﹣S△AED
=5×5﹣×3×﹣×3×4
=.
【点评】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了相似三角形的判定与性质和三角形全等的判定与性质.
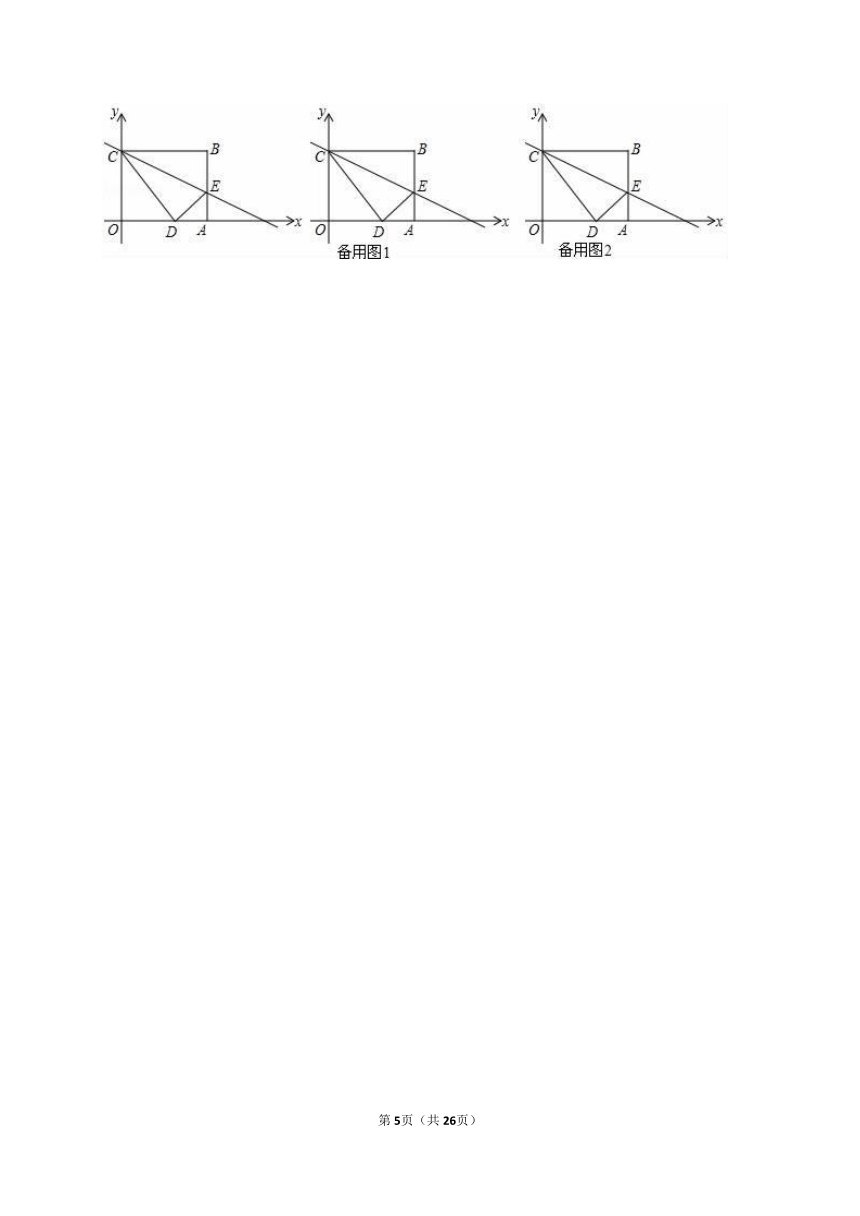
27.如图,平面直角坐标系中,矩形OABC,B(5,4),将矩形沿过点C的直线翻折,使点B落在线段OA上的点D处,折痕交AB于点E,P(m,0)是射线OA上一动点过点P作x轴的垂线,分别交直线CE和直线CB于点Q和点R.
(1)求点E的坐标;
(2)在点P的运动过程中,求的值;
(3)设直线CE交x轴于点F,过点P作x轴的垂线交直线CD于点K,连接KE,当∠CKE=∠CFO时,求出m的值和线段CQ的长.
【考点】几何变换综合题.
【分析】(1)根据题意利用勾股定理得出DO的长,进而在Rt△DAE中,DE2=AD2+AE2,得出AE的值,即可得出答案;
(2)利用PQ∥AB,得出△CQR∽△CEB,进而求出答案;
(3)首先利用相似三角形的判定方法得出△KCE∽△FCD,进而利用待定系数法求出直线CD解析式以及直线CE解析式,即可表示出K点坐标,求出m的值,再利用勾股定理得出CQ的值.
【解答】解:(1)设E(5,y),
∴AE=y,BE=4﹣y,
由题意可得:CD=BC=5,DE=BE=4﹣y,
在Rt△COD中,CO=4,
OD==3,
∴AD=AO﹣DO=5﹣3=2,
在Rt△DAE中,DE2=AD2+AE2,
∴(4﹣y)2=22+y2,
解得:y=,
∴E(5,);
(2)如图1,
∵PQ⊥x轴,
∴PQ∥AB,
∴△CQR∽△CEB,
∴===2;
(3)如图2,
∵∠CKE=∠CFO,∠KCE=∠FCD,
∴△KCE∽△FCD,
∴=,
∵C(0,4),E(5,),
设直线CE解析式为y=kx+4,
∴=5k+4,
解得:k=﹣,
∴y=﹣x+4,
∴F(8,0),
∴CF==4,CE==,
∵C(0,4),D(3,0),
∴设直线CD解析式为y=k1x+4,
∴0=3k1+4,
∴k1=﹣,
∴y=﹣x+4,
∴设K(m,﹣ m+4),
∴KR=|﹣m+4﹣4|=m,
∵CR=m,
∴CK===m,
∵=,
∴=,
解得:m=6,
∵Q在直线CE上,
∴y=﹣×6+4=1,
∴Q(6,1),
∴CQ===3.
【点评】此题主要考查了几何变换以及勾股定理、相似三角形的判定与性质、待定系数法求一次函数解析式等知识,根据题意画出正确图形,再结合相似三角形的性质求出m的值是解题关键.
第5页(共26页)
一、选择题
1.下列图形不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
2.下列方程,是一元二次方程的是( )
A.2(x﹣1)=3x B. C.2x2﹣x=0 D.x(x﹣1)=y
3.下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
4. ABCD的周长为40 cm,△ABC的周长为25 cm,则对角线AC长为( )
A.5cm B.15cm C.6cm D.16cm
5.下列命题的逆命题正确的是( )
A.如果两个角是直角,那么它们相等
B.全等三角形的面积相等
C.同位角相等,两直线平行
D.若a=b,则a2=b2
6.顺次连接对角线相等的四边形各边中点,所得到的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
7.点A(﹣5,y1)和B(﹣2,y2)都在直线y=﹣3x上,则y1与y2的关系是( )
A.y1≤y2 B.y1=y2 C.y1<y2 D.y1>y2
8.将直线y=3x﹣2平移后,得到直线y=3x+6,则原直线( )
A.沿y轴向上平移了8个单位 B.沿y轴向下平移了8个单位
C.沿x轴向左平移了8个单位 D.沿x轴向右平移了8个单位
9.等腰三角形的底和腰是方程x2﹣6x+8=0的两根,则这个三角形的周长为( )
A.8 B.10 C.8或10 D.不能确定
10.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:
①起跑后1小时内,甲在乙的前面;
②第1小时两人都跑了10千米;
③甲比乙先到达终点;
④两人都跑了20千米.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.在函数y=中,自变量x的取值范围是 .
12.函数y=3x+b(b<0)的图象不经过第 象限.
13.三角形三条中位线围成的三角形的周长为6,则它的周长是 .
14.已知一元二次方程x2+px+3=0的一个根为﹣3,则p= .
15.两直角边分别为12和16的直角三角形斜边上的中线的长是 .
16.已知菱形两条对角线的长分别为4cm和8cm,则这个菱形的面积是 ,周长是 .
17.如果一次函数y=﹣2x+b的图象交x轴于点(﹣3,0),那么关于x的不等式﹣2x+b<0的解集为 .
18.已知关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则实数k的取值范围是 .
19.已知矩形ABCD中,BE平分∠ABC交矩形的一条边于点E,若BD=10,∠EBD=15°,则AB= .
20.如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF= .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(1)用公式法解方程:x2﹣4x﹣7=0
(2)用因式分解法解方程:x(x﹣2)+x﹣2=0.
22.在所给的11×10方格中,每个小正方形的边长都是1,按要求画出四边形,使它的四个顶点都在小正方形的顶点上.
(1)在图1中画出周长为20的菱形ABCD(非正方形);
(2)在图2中画出邻边比为1:2,面积为40的矩形EFGH,并直接写出矩形EFGH对角线的长.
23.如图是长方形鸡场平面示意图,一边靠墙(墙足够长),另外三边用竹篱笆围成,在其中一边上有一个1米长的小门(用其它材料制成),若竹篱笆总长为34米,所围的面积为150平方米,求此长方形鸡场的长、宽分别为多少米?
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
25.某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.并求怎样购买使费用最少,最少费用是多少元?
26.如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1)求证:AF﹣BF=EF;
(2)若AG=,EF=1,求四边形DEGC的面积.
27.如图,平面直角坐标系中,矩形OABC,B(5,4),将矩形沿过点C的直线翻折,使点B落在线段OA上的点D处,折痕交AB于点E,P(m,0)是射线OA上一动点过点P作x轴的垂线,分别交直线CE和直线CB于点Q和点R.
(1)求点E的坐标;
(2)在点P的运动过程中,求的值;
(3)设直线CE交x轴于点F,过点P作x轴的垂线交直线CD于点K,连接KE,当∠CKE=∠CFO时,求出m的值和线段CQ的长.
2014-2015学年黑龙江省哈尔滨市道里区八年级(下)期末数学试卷
参考答案与试题解析
一、选择题
1.下列图形不是轴对称图形的是( )
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
【考点】轴对称图形.
【分析】根据轴对称图形的概念求解.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
【解答】解:A、不是轴对称图形,故选项正确;
B、是轴对称图形,故选项错误;
C、是轴对称图形,故选项错误;
D、是轴对称图形,故选项错误.
故选A.
【点评】掌握好轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.下列方程,是一元二次方程的是( )
A.2(x﹣1)=3x B. C.2x2﹣x=0 D.x(x﹣1)=y
【考点】一元二次方程的定义.
【专题】常规题型.
【分析】本题根据一元二次方程的定义解答.一元二次方程必须满足四个条件:(1)未知数的最高次数是2;(2)二次项系数不为0;
(3)是整式方程;(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
【解答】解:A、方程二次项系数为0,故本选项错误;
B、不是整式方程,故本选项错误;
C、符合一元二次方程的定义,故本选项正确;
D、有两个未知数,故本选项错误.
故选C.
【点评】本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.
3.下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6 C.5,12,13 D.4,6,7
【考点】勾股定理的逆定理.
【专题】计算题.
【分析】判断是否为直角三角形,只要验证两小边的平方和等于最长边的平方即可.
【解答】解:A、22+32=13≠42,故A选项构成不是直角三角形;
B、32+42=25≠62,故B选项构成不是直角三角形;
C、52+122=169=132,故C选项构成是直角三角形;
D、42+62=52≠72,故D选项构成不是直角三角形.
故选:C.
【点评】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
4. ABCD的周长为40 cm,△ABC的周长为25 cm,则对角线AC长为( )
A.5cm B.15cm C.6cm D.16cm
【考点】平行四边形的性质.
【分析】由 ABCD的周长为40 cm,可得AB+BC=20cm,又有△ABC的周长为25 cm,即可求对角线AC长.
【解答】解:∵ ABCD的周长为40 cm,
∴AB+BC=20cm,
又∵△ABC的周长为25 cm,
∴对角线AC长为25﹣20=5cm.
故选A.
【点评】此题主要考查平行四边的性质:平行四边形的两组对边分别相等.
5.下列命题的逆命题正确的是( )
A.如果两个角是直角,那么它们相等
B.全等三角形的面积相等
C.同位角相等,两直线平行
D.若a=b,则a2=b2
【考点】命题与定理.
【分析】交换原命题的题设与结论得到四个命题的逆命题,然后分别根据直角的定义、全等三角形的判定、平行线的性质和平方根的定义判定四个逆命题的真假.
【解答】解:A、逆命题为:如果两个角相等,那么它们都是直角,此逆命题为假命题;
B、逆命题为:面积相等的两三角形全等,此逆命题为假命题;
C、逆命题为:两直线平行,同位角相等,此逆命题为真命题;
D、逆命题为,若a2=b2,则a=b,此逆命题为假命题.
故选C.
【点评】本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆命题.
6.顺次连接对角线相等的四边形各边中点,所得到的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
【考点】三角形中位线定理;菱形的判定.
【分析】首先根据三角形的中位线定理,得新四边形各边都等于原四边形的对角线的一半;
再结合原四边形的对角线相等,从而得到新四边形各边相等,根据菱形的判定方法知新四边形即为菱形.
【解答】解:根据三角形的中位线定理,得
新四边形各边都等于原四边形的对角线的一半.
又∵原四边形的对角线相等,
∴新四边形各边相等,
根据四边相等的四边形是菱形,得新四边形为菱形.
故选B.
【点评】本题主要考查了三角形的中位线定理和菱形的判定方法.
7.点A(﹣5,y1)和B(﹣2,y2)都在直线y=﹣3x上,则y1与y2的关系是( )
A.y1≤y2 B.y1=y2 C.y1<y2 D.y1>y2
【考点】一次函数图象上点的坐标特征.
【分析】根据一次函数的性质即可作出判断.
【解答】解:∵一次函数中一次项系数﹣3<0,﹣5<﹣2,
∴y1>y2.
故选D
【点评】本题考查了一次函数的性质,在解析式y=kx+b(k≠0,且k,b是常数)中,当k<0时,y随x的增大而减小.
8.将直线y=3x﹣2平移后,得到直线y=3x+6,则原直线( )
A.沿y轴向上平移了8个单位 B.沿y轴向下平移了8个单位
C.沿x轴向左平移了8个单位 D.沿x轴向右平移了8个单位
【考点】一次函数图象与几何变换.
【分析】利用一次函数图象的平移规律,左加右减,上加下减,得出即可.
【解答】解:∵将直线y=3x﹣2平移后,得到直线y=3x+6,
∴3x﹣2+a=3x+6,
解得:a=8,
所以沿y轴向上平移了8个单位,
故选A
【点评】此题主要考查了一次函数图象与几何变换,正确把握变换规律是解题关键.
9.等腰三角形的底和腰是方程x2﹣6x+8=0的两根,则这个三角形的周长为( )
A.8 B.10 C.8或10 D.不能确定
【考点】等腰三角形的性质;解一元二次方程-因式分解法;三角形三边关系.
【专题】计算题.
【分析】先求出方程的根,再根据三角形三边关系确定是否符合题意,然后求解.
【解答】解:∵方程x2﹣6x+8=0的解是x=2或4,
(1)当2为腰,4为底时,2+2=4不能构成三角形;
(2)当4为腰,2为底时,4,4,2能构成等腰三角形,周长=4+4+2=10.
故选:B.
【点评】本题考查了等腰三角形的性质和分情况讨论的思想,注意根据三角形的三边关系确定是否能构成三角形,不可盲目讨论.
10.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:
①起跑后1小时内,甲在乙的前面;
②第1小时两人都跑了10千米;
③甲比乙先到达终点;
④两人都跑了20千米.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
【考点】函数的图象.
【专题】压轴题.
【分析】由图象可知起跑后1小时内,甲在乙的前面;在跑了1小时时,乙追上甲,此时都跑了10千米;乙比甲先到达终点;求得乙跑的直线的解析式,即可求得两人跑的距离,则可求得答案.
【解答】解:根据图象得:
起跑后1小时内,甲在乙的前面;故①正确;
在跑了1小时时,乙追上甲,此时都跑了10千米,故②正确;
乙比甲先到达终点,故③错误;
设乙跑的直线解析式为:y=kx,
将点(1,10)代入得:k=10,
∴解析式为:y=10x,
∴当x=2时,y=20,
∴两人都跑了20千米,故④正确.
所以①②④三项正确.
故选:C.
【点评】此题考查了函数图形的意义.解题的关键是根据题意理解各段函数图象的实际意义,正确理解函数图象横纵坐标表示的意义,理解问题的过程.
二、填空题
11.在函数y=中,自变量x的取值范围是 x≠﹣ .
【考点】函数自变量的取值范围.
【分析】根据分母不等于0列式计算即可得解.
【解答】解:由题意得,3x+2≠0,
解得x≠﹣.
故答案为:x≠﹣.
【点评】本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
12.函数y=3x+b(b<0)的图象不经过第 二 象限.
【考点】一次函数图象与系数的关系.
【分析】根据一次函数的图象与系数的关系即可得出结论.
【解答】解:∵函数y=3x+b(b<0)中,k=3>0,b<0,
∴此函数的图象经过一、三、四象限,不经过第二象限.
故答案为:二.
【点评】本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k>0,b<0时函数的图象在一、三、四象限是解答此题的关键.
13.三角形三条中位线围成的三角形的周长为6,则它的周长是 12 .
【考点】三角形中位线定理.
【专题】计算题.
【分析】根据三角形的中位线定理知:三条中位线围成的三角形的各边是对应原三角形各边的一半,所以原三角形的周长是12.
【解答】解:根据题意可知,原三角形的周长=2×6=12.
故答案为:12.
【点评】本题考查了三角形中位线定理的数量关系:三角形的中位线等于第三边的一半.
14.已知一元二次方程x2+px+3=0的一个根为﹣3,则p= 4 .
【考点】一元二次方程的解.
【分析】已知一元二次方程x2+px+3=0的一个根为﹣3,因而把x=﹣3代入方程即可求得p的值.
【解答】解:把x=﹣3代入方程可得:(﹣3)2﹣3p+3=0,
解得p=4
故填:4.
【点评】本题主要考查了方程的解的定义,把求未知系数的问题转化为方程求解的问题.
15.两直角边分别为12和16的直角三角形斜边上的中线的长是 10 .
【考点】直角三角形斜边上的中线;勾股定理.
【分析】根据勾股定理求出斜边长,根据直角三角形斜边上的中线等于斜边的一半求出答案.
【解答】解:∵两直角边分别为12和16,
∴斜边==20,
∴斜边上的中线的长为10,
故答案为:10.
【点评】本题考查的是直角三角形的性质和勾股定理,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.
16.已知菱形两条对角线的长分别为4cm和8cm,则这个菱形的面积是 16 ,周长是 8 .
【考点】菱形的性质.
【分析】根据菱形的面积公式:两对角线乘积的一半,求得菱形的面积;再由菱形的两对角线的一半和勾股定理求得菱形的边长,进而求出周长.
【解答】解:菱形的面积=(4×8)÷2=18cm2.
菱形的边长==2,
∴周长=4×2=8.
故答案为:16,.
【点评】本题主要利用勾股定理求边长和菱形的面积公式:“对角线乘积的一半”来解决.
17.如果一次函数y=﹣2x+b的图象交x轴于点(﹣3,0),那么关于x的不等式﹣2x+b<0的解集为 x<﹣3 .
【考点】一次函数与一元一次不等式.
【分析】根据题意画出函数图象,利用数形结合即可得出结论.
【解答】解:如图所示,关于x的不等式﹣2x+b<0的解集为x<﹣3.
故答案为:x<﹣3.
【点评】本题考查的是一次函数与一元一次不等式,能利用数形结合求出不等式的取值范围是解答此题的关键.
18.已知关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则实数k的取值范围是 k>﹣1且k≠0. .
【考点】根的判别式.
【专题】计算题.
【分析】根据一元二次方程的定义以及根的判别式得到k≠0,且△>0,然后解两个不等式即可得到实数k的取值范围.
【解答】解:根据题意得,k≠0,且△>0,即22﹣4×k×(﹣1)>0,解得k>﹣1,
∴实数k的取值范围为k>﹣1且k≠0.
故答案为k>﹣1且k≠0.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根;也考查了一元二次方程的定义.
19.已知矩形ABCD中,BE平分∠ABC交矩形的一条边于点E,若BD=10,∠EBD=15°,则AB= 5或5 .
【考点】矩形的性质;含30度角的直角三角形.
【专题】分类讨论.
【分析】化成符合条件的两种情况,根据矩形性质求出∠A=∠ABC=∠C=90°,∠ABE=∠CBE=45°,求出∠DBC和∠ABD的度数,求出CD和AD,即可求出AB.
【解答】解:有两种情况:如图
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠C=90°,
∵BE平分∠ABC,
∴∠ABE=∠CBE=45°,
图1中,∵∠EBD=15°,
∴∠DBC=30°,
∴CD=BD=5,
即AB=CD=5;
图2中,∵∠EBD=15°,
∴∠ABD=30°,
∴AD=BD=5,
在Rt△ABD中,由勾股定理得:AB==5.
故答案为:5或5.
【点评】本题考查了矩形性质和含30度角的直角三角形性质,勾股定理的应用,关键是化成符合条件的所有情况,题目比较典型,是一道比较好的题目.
20.如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF= .
【考点】菱形的性质;翻折变换(折叠问题).
【专题】计算题.
【分析】DE和CB的延长线相交于G'点,连结EF,作EH⊥DF于H点,如图,根据菱形的性质得A=180°﹣∠B=120°,AB=AD=2,AD∥BC,则∠1=∠G,再利用折叠的性质得∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,则∠4=60°,在Rt△EHG中利用含30度的直角三角形三边的关系得到HG=EG=,EH=EH=,则在Rt△DEH中利用勾股定理可计算出DE=,再证明∠2=∠G'得到FG'=FD,证明△AED≌△BEG'得到DE=G'E,所以FE⊥DG',然后证明Rt△DEF∽Rt△DHE,利用相似比计算出DF=,则FG=FD﹣DG=,于是得到BF=FG=.
【解答】解DE和CB的延长线相交于G’点,连结EF,作EH⊥DF于H点,如图,
∵四边形ABCD为菱形,
∴∠A=180°﹣∠B=120°,AB=AD=2,AD∥BC
∴∠1=∠G',
而E为AB的中点,
∴AE=BE=1,
∵△AED沿DE翻折得到△GED,
∴∠1=∠2,DG=DA=2,EG=EA=1,∠3=∠A=120°,
∴∠4=60°,
在Rt△EHG中,HG=EG=,EH=EH=,
在Rt△DEH中,DE===,
∵AD∥BG',
∴∠1=∠G',
∴∠G'=∠2,
∴FG=FD,
在△AED和△BEG'中,
,
∴△AED≌△BEG',
∴DE=G'E,
∴FE⊥DG',
∴∠FED=90°,
∵∠HDE=∠EDF,
∴Rt△DEF∽Rt△DHE,
∴=,即=,
∴DF=,
∴FG=FD﹣DG=﹣2=,
∴BF=FG=.
故答案为.
【点评】本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了折叠的性质、全等三角形的判定与性质和相似三角形的判定与性质.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(1)用公式法解方程:x2﹣4x﹣7=0
(2)用因式分解法解方程:x(x﹣2)+x﹣2=0.
【考点】解一元二次方程-因式分解法;解一元二次方程-公式法.
【专题】计算题.
【分析】(1)方程利用公式法求出解即可;
(2)方程利用因式分解法求出解即可.
【解答】解:(1)这里a=1,b=﹣4,c=﹣7,
∵△=16+28=44,
∴x==2±;
(2)分解因式得:(x﹣2)(x+1)=0,
可得x﹣2=0或x+1=0,
解得:x1=2,x2=﹣1.
【点评】此题考查了解一元二次方程﹣因式分解法,熟练掌握因式分解的方法是解本题的关键.
22.在所给的11×10方格中,每个小正方形的边长都是1,按要求画出四边形,使它的四个顶点都在小正方形的顶点上.
(1)在图1中画出周长为20的菱形ABCD(非正方形);
(2)在图2中画出邻边比为1:2,面积为40的矩形EFGH,并直接写出矩形EFGH对角线的长.
【考点】作图—应用与设计作图;菱形的性质;矩形的性质.
【分析】(1)由菱形的周长为20,可得边长为5,即作直角边分别为3和4的直角三角形,则斜边为5,即可得到菱形ABCD;
(2)利用已知条件可求出矩形的长和宽,进而可画出矩形EFGH,利用勾股定理可求出其对角线的长.
【解答】解:(1)如图所示:
(2)∵矩形EFGH的面积=40,长:宽=2:1,
∴长=4,宽=2,
∴其对角线EG=FH==10,
如图所示:
【点评】此题主要考查了应用设计与作图以及勾股定理和菱形、矩形的性质,正确借助网格得出是解题关键.
23.如图是长方形鸡场平面示意图,一边靠墙(墙足够长),另外三边用竹篱笆围成,在其中一边上有一个1米长的小门(用其它材料制成),若竹篱笆总长为34米,所围的面积为150平方米,求此长方形鸡场的长、宽分别为多少米?
【考点】一元二次方程的应用.
【专题】几何图形问题.
【分析】设长方形鸡场的长为x米,则宽为(34+1﹣x)米,由此根据长方形的面积计算方法由所围的面积为150平方米,建立方程解决问题.
【解答】解:设长方形鸡场的长为x米,则宽为(34+1﹣x)米,由题意得
x (34+1﹣x)=150
解得:x1=15,x2=20
当x=15时,(34+1﹣x)=10,
当x=20时,(34+1﹣x)=7.5,
答:长方形鸡场的长为15米,宽为10米或长方形鸡场的长为20米,宽为7.5米.
【点评】此题考查一元二次方程的实际运用,掌握长方形的周长和面积计算公式是解决问题的前提.
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
【考点】菱形的性质;矩形的判定与性质.
【分析】(1)先求出四边形OCED是平行四边形,再根据菱形的对角线互相垂直求出∠COD=90°,证明OCED是矩形,可得OE=CD即可;
(2)根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
【解答】(1)证明:在菱形ABCD中,OC=AC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=4.
∴在矩形OCED中,CE=OD==2.
在Rt△ACE中,
AE==2.
【点评】本题考查了菱形的性质,矩形的判定与性质,勾股定理的应用,是基础题,熟记矩形的判定方法与菱形的性质是解题的关键.
25.某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.并求怎样购买使费用最少,最少费用是多少元?
【考点】一次函数的应用;二元一次方程组的应用;一元一次不等式的应用.
【分析】(1)设A奖品的单价是x元,B奖品的单价是y元,根据条件建立方程组求出其解即可;
(2)根据总费用=两种奖品的费用之和表示出W与m的关系式,并有条件建立不等式组求出x的取值范围,由一次函数的性质就可以求出结论.
【解答】解(1)设A奖品的单价是x元,B奖品的单价是y元,由题意,得
,
解得:.
答:A奖品的单价是10元,B奖品的单价是15元;
(2)由题意,得
W=10m+15(100﹣m)=﹣5m+1500
∴m≤3(100﹣m),
解得:m≤75,
∵W=﹣5m+1500,
∴k=﹣5<0,
∴W随m的增大而减小,
∴m=75时,W最小=1125,
∴应买A种奖品75件,B种奖品25件,才能使总费用最少为1125元.
【点评】本题考查了一次函数的性质的运用,二元一次方程组的运用,一元一次不等式组的运用,解答时求一次函数的解析式是关键.
26.如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1)求证:AF﹣BF=EF;
(2)若AG=,EF=1,求四边形DEGC的面积.
【考点】正方形的性质;全等三角形的判定与性质.
【分析】(1)先利用等角的余角相等得到∠BAF=∠ADE,则可根据”AAS“判定△ABF≌△DAE,得到BF=AE,所以AF﹣BF=AF﹣AE=EF;
(2)设AE=BF=a,则AF=a+1,由(1)得△ABF≌△DAE,所以DE=AF=a+1,在Rt△ADE中利用勾股定理得到AD2=a2+(a+1)2,再证明Rt△ABF∽Rt△AGB,利用相似比得AB2=AF AG=(a+1)×,所以a2+(a+1)2=(a+1)×,整理得8a2﹣17a﹣21=0,解得a1=3,a2=﹣(舍去),即可得到AB=5,然后利用四边形DEGC的面积=S正方形ABCD﹣S△ABG﹣S△AED进行计算.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵E⊥AG于点E,BF⊥AG于点F,
∴∠AED=∠BFA=90°,
∴∠DAE+∠ADE=90°,
而∠DAE+∠BAF=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE,
∴BF=AE,
∴AF﹣BF=AF﹣AE=EF;
(2)解:设AE=BF=a,则AF=a+1,
∵△ABF≌△DAE,
∴DE=AF=a+1,
在Rt△ADE中,AD2=a2+(a+1)2,
∵∠BAF=∠GAB,
∴Rt△ABF∽Rt△AGB,
∴AB:AG=AF:AB,
∴AB2=AF AG=(a+1)×,
而AB=AD,
∴a2+(a+1)2=(a+1)×,
整理得8a2﹣17a﹣21=0,解得a1=3,a2=﹣(舍去),
∴AB==5,
∴四边形DEGC的面积=S正方形ABCD﹣S△ABG﹣S△AED
=5×5﹣×3×﹣×3×4
=.
【点评】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了相似三角形的判定与性质和三角形全等的判定与性质.
27.如图,平面直角坐标系中,矩形OABC,B(5,4),将矩形沿过点C的直线翻折,使点B落在线段OA上的点D处,折痕交AB于点E,P(m,0)是射线OA上一动点过点P作x轴的垂线,分别交直线CE和直线CB于点Q和点R.
(1)求点E的坐标;
(2)在点P的运动过程中,求的值;
(3)设直线CE交x轴于点F,过点P作x轴的垂线交直线CD于点K,连接KE,当∠CKE=∠CFO时,求出m的值和线段CQ的长.
【考点】几何变换综合题.
【分析】(1)根据题意利用勾股定理得出DO的长,进而在Rt△DAE中,DE2=AD2+AE2,得出AE的值,即可得出答案;
(2)利用PQ∥AB,得出△CQR∽△CEB,进而求出答案;
(3)首先利用相似三角形的判定方法得出△KCE∽△FCD,进而利用待定系数法求出直线CD解析式以及直线CE解析式,即可表示出K点坐标,求出m的值,再利用勾股定理得出CQ的值.
【解答】解:(1)设E(5,y),
∴AE=y,BE=4﹣y,
由题意可得:CD=BC=5,DE=BE=4﹣y,
在Rt△COD中,CO=4,
OD==3,
∴AD=AO﹣DO=5﹣3=2,
在Rt△DAE中,DE2=AD2+AE2,
∴(4﹣y)2=22+y2,
解得:y=,
∴E(5,);
(2)如图1,
∵PQ⊥x轴,
∴PQ∥AB,
∴△CQR∽△CEB,
∴===2;
(3)如图2,
∵∠CKE=∠CFO,∠KCE=∠FCD,
∴△KCE∽△FCD,
∴=,
∵C(0,4),E(5,),
设直线CE解析式为y=kx+4,
∴=5k+4,
解得:k=﹣,
∴y=﹣x+4,
∴F(8,0),
∴CF==4,CE==,
∵C(0,4),D(3,0),
∴设直线CD解析式为y=k1x+4,
∴0=3k1+4,
∴k1=﹣,
∴y=﹣x+4,
∴设K(m,﹣ m+4),
∴KR=|﹣m+4﹣4|=m,
∵CR=m,
∴CK===m,
∵=,
∴=,
解得:m=6,
∵Q在直线CE上,
∴y=﹣×6+4=1,
∴Q(6,1),
∴CQ===3.
【点评】此题主要考查了几何变换以及勾股定理、相似三角形的判定与性质、待定系数法求一次函数解析式等知识,根据题意画出正确图形,再结合相似三角形的性质求出m的值是解题关键.
第5页(共26页)
同课章节目录
