2025年山东省济南天桥区泺口实验中学七年级下学期数学第一次月考试卷(含答案)
文档属性
| 名称 | 2025年山东省济南天桥区泺口实验中学七年级下学期数学第一次月考试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 153.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 14:16:26 | ||
图片预览


文档简介
七年级下学期数学第一次月考试卷(3.14)
(满分150分 时间:120分钟)
一、选择题:(每小题4分,共40分)
1.计算a2·a4结果正确的是( )
A .a2 B .a6 C .a8 D .2a2
2.在科研人员的不懈努力下,我国成功制造出了"超薄钢",打破了日德垄断,据悉,该材料的厚度仅有0.000015米,将数据0.000015用科学记数法表示为( )
A .1.5×10-5 B .1.5×10-4 C.15×10-4 D .0.15×10﹣6
3.下列运算正确的是( )
A .3a- a =2a2 B . a3·a2 = a6 C .( ab )2=ab2 D .(-a3)2= a6
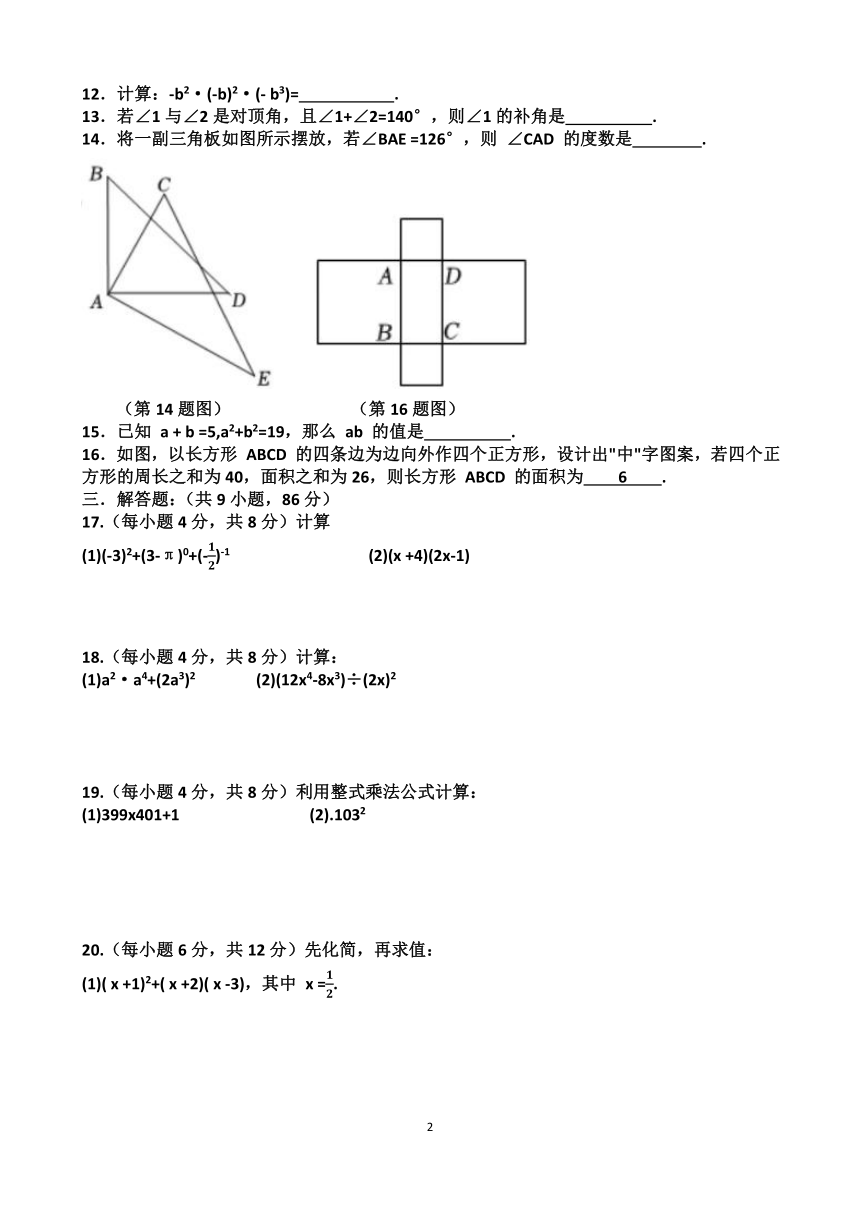
4.在下列图中,∠1与∠2属于对顶角的是( )
5.如图, A , B , C , D 四点在直线上,点 M 在直线外,MC⊥l,若 MA =5cm, MB =4cm, MC=2cm, MD =3cm,则点 M 到直线l的距离是( )
A.2cm B .3cm C .4cm D . 5cm
(第5题图) (第9题图) (第10题图)
6.下列多项式相乘,能用平方差公式计算的是( )
A .(2a-3b)(3b+2a) B .(2a+ b )(2b- a ) C .(3m- n )(-3m+ n ) D .(m -n)(﹣n +m )
7.下列各式中,能用完全平方公式计算的是( )
A .(2a-3b)(-2a-3b) B .( a +3b)( a +3b) C .( a -3b( a +3b) D .(3a-4b)(4a+3b)
8.若∠A 和 ∠B 互为余角, ∠B 与 ∠C 互补,且∠C=130°,则∠A的度数为( B )
A .30° B .40° C.40 D .60°
9.有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示,右边场地为长方形,长为2( a + b ),则宽为( )
A .( a - b ) B . a - b C .( a + b ) D . a + b
10.如图所示的图形由一个大正方形 ABEF 、一个小正方形 ADGH 和一个长方形 ABCD 不重合无缝隙得拼接在一起,已知长方形 ABCD 的面积是6,正方形 ABEF 和正方形 ADGH 的面积之和为69,那么长方形 ABCD 的周长是( )
A .12 B .18 C .16 D .14
二、填空题:(每小题4分,共24分)
11.己知10m=4,10n=5,则10m+n= .
12.计算:-b2·(-b)2·(- b3)= .
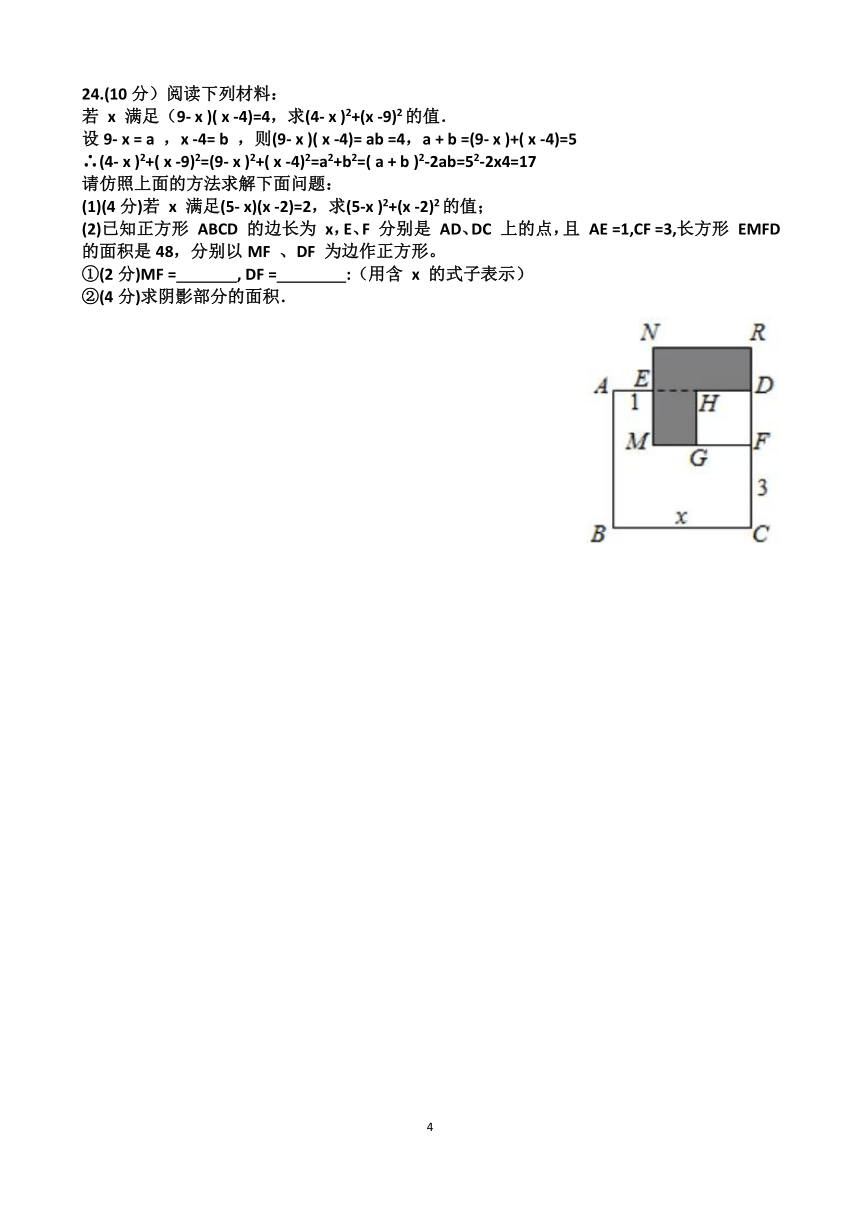
13.若∠1与∠2是对顶角,且∠1+∠2=140°,则∠1的补角是 .
14.将一副三角板如图所示摆放,若∠BAE =126°,则 ∠CAD 的度数是 .
(第14题图) (第16题图)
15.已知 a + b =5,a2+b2=19,那么 ab 的值是 .
16.如图,以长方形 ABCD 的四条边为边向外作四个正方形,设计出"中"字图案,若四个正方形的周长之和为40,面积之和为26,则长方形 ABCD 的面积为 6 .
三.解答题:(共9小题,86分)
17.(每小题4分,共8分)计算
(1)(-3)2+(3-π)0+(-)-1 (2)(x +4)(2x-1)
18.(每小题4分,共8分)计算:
(1)a2·a4+(2a3)2 (2)(12x4-8x3)÷(2x)2
19.(每小题4分,共8分)利用整式乘法公式计算:
(1)399x401+1 (2).1032
20.(每小题6分,共12分)先化简,再求值:
(1)( x +1)2+( x +2)( x -3),其中 x =.
(2)已知2a2+3a-4=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值。
21、(6分)已知一个角的补角是这个角的余角的3倍,求这个角的度数.
22.(第(1)题6分,第(2)题4分,共10分)如图,某市有一块长为(3a+ b )米,宽为(2a+ b )米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像。
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当 a =3, b =2时的绿化面积.
23.(12分)阅读材料:如果一个数的平方等于﹣1,记为 i2 =-1,这个数i叫做虚数单位,那么形如 a + bi ( a, b 为实数)的数就叫做复数,a 叫这个复数的实部,b叫做这个复数的虚部.
4+4i+i2
它有如下特点:
①它的加,减,乘法运算与整式的加,减,乘法运算类似,例如计算:
(2+i)+(3-4i)=(2+3)+(1-4) i =5-3i,(3+ i ) i =3i+i2=3i-1.
②若两个复数,它们的实部和虚部分别相等,则称这两个复数相等;若它们的实部相等,虚
部互为相反数,则称这两个复数共轭;如1+2i的共轭复数为1-2i.
(1)(4分)填空:①(2+i)(2-i)= ; ②(2+i)2= .
(2)(4分)若 a + bi 是(1+2i)2的共轭复数,求(b - a )2的值;
(3)(4分)已知(a + i )(b + i )=1-3i,求(a2+b2) ( i +i2+i3+...+i2025)的值.
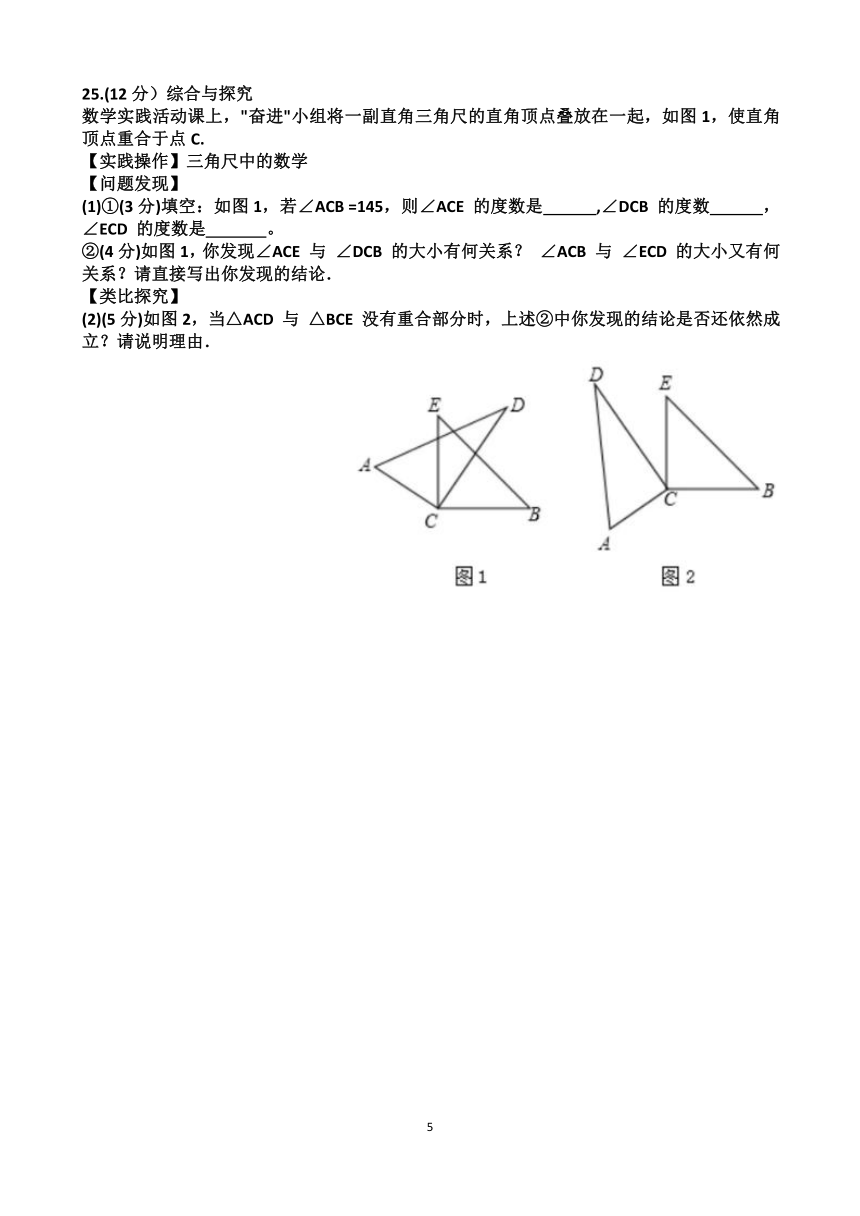
24.(10分)阅读下列材料:
若 x 满足(9- x )( x -4)=4,求(4- x )2+(x -9)2的值.
设9- x = a ,x -4= b ,则(9- x )( x -4)= ab =4,a + b =(9- x )+( x -4)=5
∴(4- x )2+( x -9)2=(9- x )2+( x -4)2=a2+b2=( a + b )2-2ab=52-2x4=17
请仿照上面的方法求解下面问题:
(1)(4分)若 x 满足(5- x)(x -2)=2,求(5-x )2+(x -2)2的值;
(2)已知正方形 ABCD 的边长为 x,E、F 分别是 AD、DC 上的点,且 AE =1,CF =3,长方形 EMFD 的面积是48,分别以MF 、DF 为边作正方形。
①(2分)MF = , DF = :(用含 x 的式子表示)
②(4分)求阴影部分的面积.
25.(12分)综合与探究
数学实践活动课上,"奋进"小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
【实践操作】三角尺中的数学
【问题发现】
(1)①(3分)填空:如图1,若∠ACB =145,则∠ACE 的度数是 ,∠DCB 的度数 ,∠ECD 的度数是 。
②(4分)如图1,你发现∠ACE 与 ∠DCB 的大小有何关系? ∠ACB 与 ∠ECD 的大小又有何关系?请直接写出你发现的结论.
【类比探究】
(2)(5分)如图2,当△ACD 与 △BCE 没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
答案
一、选择题:(每小题4分,共40分)
1.计算a2·a4结果正确的是( B )
A .a2 B .a6 C .a8 D .2a2
2.在科研人员的不懈努力下,我国成功制造出了"超薄钢",打破了日德垄断,据悉,该材料的厚度仅有0.000015米,将数据0.000015用科学记数法表示为( A )
A .1.5×10-5 B .1.5×10-4 C.15×10-4 D .0.15×10﹣6
3.下列运算正确的是( D )
A .3a- a =2a2 B . a3·a2 = a6 C .( ab )2=ab2 D .(-a3)2= a6
4.在下列图中,∠1与∠2属于对顶角的是( B )
5.如图, A , B , C , D 四点在直线上,点 M 在直线外,MC⊥l,若 MA =5cm, MB =4cm, MC=2cm, MD =3cm,则点 M 到直线l的距离是( C )
A.2cm B .3cm C .4cm D . 5cm
(第5题图) (第9题图) (第10题图)
6.下列多项式相乘,能用平方差公式计算的是( A )
A .(2a-3b)(3b+2a) B .(2a+ b )(2b- a ) C .(3m- n )(-3m+ n ) D .(m -n)(﹣n +m )
7.下列各式中,能用完全平方公式计算的是( B )
A .(2a-3b)(-2a-3b) B .( a +3b)( a +3b) C .( a -3b( a +3b) D .(3a-4b)(4a+3b)
8.若∠A 和 ∠B 互为余角, ∠B 与 ∠C 互补,且∠C=130°,则∠A的度数为( B )
A .30° B .40° C.40 D .60°
9.有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示,右边场地为长方形,长为2( a + b ),则宽为( C )
A .( a - b ) B . a - b C .( a + b ) D . a + b
10.如图所示的图形由一个大正方形 ABEF 、一个小正方形 ADGH 和一个长方形 ABCD 不重合无缝隙得拼接在一起,已知长方形 ABCD 的面积是6,正方形 ABEF 和正方形 ADGH 的面积之和为69,那么长方形 ABCD 的周长是( B )
A .12 B .18 C .16 D .14
二、填空题:(每小题4分,共24分)
11.己知10m=4,10n=5,则10m+n= 20 .
12.计算:-b2·(-b)2·(- b3)= b7 .
13.若∠1与∠2是对顶角,且∠1+∠2=140°,则∠1的补角是 110° .
14.将一副三角板如图所示摆放,若∠BAE =126°,则 ∠CAD 的度数是 54° .
(第14题图) (第16题图)
15.已知 a + b =5,a2+b2=19,那么 ab 的值是 3 .
16.如图,以长方形 ABCD 的四条边为边向外作四个正方形,设计出"中"字图案,若四个正方形的周长之和为40,面积之和为26,则长方形 ABCD 的面积为 6 .
三.解答题:(共9小题,86分)
17.(每小题4分,共8分)计算
(1)(-3)2+(3-π)0+(-)-1 (2)(x +4)(2x-1)
=9+1﹣2 =2x2﹣x+8x﹣4
=8 =2x2+7x﹣4
18.(每小题4分,共8分)计算:
(1)a2·a4+(2a3)2 (2)(12x4-8x3)÷(2x)2
=a6+4a6 =(12x4-8x3)÷(4x2)
=5a6 =3x2﹣2x
19.(每小题4分,共8分)利用整式乘法公式计算:
(1)399x401+1 (2).1032
=(400﹣1)(400+1)+1 =(100+3)2
=4002﹣1+1 =1002+×100×3+32
=160000 =10609
20.(每小题6分,共12分)先化简,再求值:
(1)( x +1)2+( x +2)( x -3),其中 x =.
解:原式=x2+2x+1+x2﹣3x+2x﹣6
=2x2+x﹣5
将x =代入得:2×+﹣5=﹣4
(2)已知2a2+3a-4=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值。
解:原式=6a2+3a﹣4a2+1
=2a2+3a+1
将2a2+3a=4代入得4+1=5
21、(6分)已知一个角的补角是这个角的余角的3倍,求这个角的度数.
解设这个角为x,则
180°﹣x=3(90°﹣x)
解得 x=45°
答:这个角为45°
22.(第(1)题6分,第(2)题4分,共10分)如图,某市有一块长为(3a+ b )米,宽为(2a+ b )米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像。
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当 a =3, b =2时的绿化面积.
(3a+b)(2a+b)﹣(a+b)2
=6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2
=(5a2+3ab)平方米
(2)a =3, b =2代入得:5×32+3×3×2=63平方米
23.(12分)阅读材料:如果一个数的平方等于﹣1,记为 i2 =-1,这个数i叫做虚数单位,那么形如 a + bi ( a, b 为实数)的数就叫做复数,a 叫这个复数的实部,b叫做这个复数的虚部.
4+4i+i2
它有如下特点:
①它的加,减,乘法运算与整式的加,减,乘法运算类似,例如计算:
(2+i)+(3-4i)=(2+3)+(1-4) i =5-3i,(3+ i ) i =3i+i2=3i-1.
②若两个复数,它们的实部和虚部分别相等,则称这两个复数相等;若它们的实部相等,虚
部互为相反数,则称这两个复数共轭;如1+2i的共轭复数为1-2i.
(1)(4分)填空:①(2+i)(2-i)= ; ②(2+i)2= .
(2)(4分)若 a + bi 是(1+2i)2的共轭复数,求(b - a )2的值;
(3)(4分)已知(a + i )(b + i )=1-3i,求(a2+b2) ( i +i2+i3+...+i2025)的值.
(1)①5 ②3+4i
(2)(1+2i)2=1+4i﹣4=﹣3+4i
∵ a + bi 是(1+2i)2的共轭复数
∴a=﹣3,b=﹣4
(b - a )2=1
(3)(a + i )(b + i )=ab+ai+bi﹣1=ab﹣1+(a+b)i=1-3i
∴ab=2,a+b=﹣3
(a2+b2) ( i +i2+i3+...+i2025)
=(a2+b2)i
=5i
24.(10分)阅读下列材料:
若 x 满足(9- x )( x -4)=4,求(4- x )2+(x -9)2的值.
设9- x = a ,x -4= b ,则(9- x )( x -4)= ab =4,a + b =(9- x )+( x -4)=5
∴(4- x )2+( x -9)2=(9- x )2+( x -4)2=a2+b2=( a + b )2-2ab=52-2x4=17
请仿照上面的方法求解下面问题:
(1)(4分)若 x 满足(5- x)(x -2)=2,求(5-x )2+(x -2)2的值;
(2)已知正方形 ABCD 的边长为 x,E、F 分别是 AD、DC 上的点,且 AE =1,CF =3,长方形 EMFD 的面积是48,分别以MF 、DF 为边作正方形。
①(2分)MF = , DF = :(用含 x 的式子表示)
②(4分)求阴影部分的面积.
(1)设5- x = a , x -2= b .则(5- x )( x -2)= ab =2,a + b =5- x + x -2=3.
∴(5- x )2+( x -2)2=a2+b2=( a + b )2-2ab=32-2x2=9-4=5.
①∵正方形 ABCD 的边长为 x , AE =1, CF =3
∴MF = ED = AD - AE = x -1,DF = CD - CF = x -3.
②阴影部分面积等于以 MF 为边的正方形面积减去以 DF为边的正方形面积,即(x -1)2-( x -3)2
∵长方形 EMFD 的面积是48,( x -1)( x -3)=48.
设 x -1= a ,3- x = b
∴ab =-48,a + b = x -1+3- x =2
∴a- b = x -1+ x -3= MF + DF >0.
∴( x -1)2+( x -3)2=( x -1)2+(3- x )2=a2+b2=( a + b )2-2ab=22-2x(-48)=100.
∴( a - b )2=a2+b2-2ab=100-2x(-48)=196.
∵a + b >0
∴a - b =14.
∴( x -1)2-( x -3)2=( x -1)2-(3- x )2=a2-b2=( a + b )( a - b )=2×14=28.
25.(12分)综合与探究
数学实践活动课上,"奋进"小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点 C
【实践操作】三角尺中的数学
【问题发现】
(1)①(3分)填空:如图1,若∠ACB =145,则∠ACE 的度数是 ,∠DCB 的度数 ,∠ECD 的度数是 。
②(4分)如图1,你发现∠ACE 与 ∠DCB 的大小有何关系? ∠ACB 与 ∠ECD 的大小又有何关系?请直接写出你发现的结论.
【类比探究】
(2)(5分)如图2,当△ACD 与 △BCE 没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
①∠ACE =∠DCB =145°-90°=55° ,∠ECD =∠BCE -∠BCD =90°-55°=35°
②∠ACE = ∠DCB ,∠ACB + ∠ECD =180
(2)答:当△ACD 与△BCE 没有重合部分时,上述②中发现的结论依然成立.
理由:∵∠ACD =∠ECB =90°
∴∠ACD +∠ DCE =∠ ECB +∠ DCE
∴∠ACE =∠DCB
∵∠ACD = ∠ECB =90°
∴∠ACD + ∠ECB =180°
∵∠ACD +∠ECD +∠ECB +∠ACB =360°
∴∠ACB +∠ECD =180°
∴∠ACE =∠DCB , ∠ACB +∠ECD =180°
所以上述②中发现的结论依然成立.
(满分150分 时间:120分钟)
一、选择题:(每小题4分,共40分)
1.计算a2·a4结果正确的是( )
A .a2 B .a6 C .a8 D .2a2
2.在科研人员的不懈努力下,我国成功制造出了"超薄钢",打破了日德垄断,据悉,该材料的厚度仅有0.000015米,将数据0.000015用科学记数法表示为( )
A .1.5×10-5 B .1.5×10-4 C.15×10-4 D .0.15×10﹣6
3.下列运算正确的是( )
A .3a- a =2a2 B . a3·a2 = a6 C .( ab )2=ab2 D .(-a3)2= a6
4.在下列图中,∠1与∠2属于对顶角的是( )
5.如图, A , B , C , D 四点在直线上,点 M 在直线外,MC⊥l,若 MA =5cm, MB =4cm, MC=2cm, MD =3cm,则点 M 到直线l的距离是( )
A.2cm B .3cm C .4cm D . 5cm
(第5题图) (第9题图) (第10题图)
6.下列多项式相乘,能用平方差公式计算的是( )
A .(2a-3b)(3b+2a) B .(2a+ b )(2b- a ) C .(3m- n )(-3m+ n ) D .(m -n)(﹣n +m )
7.下列各式中,能用完全平方公式计算的是( )
A .(2a-3b)(-2a-3b) B .( a +3b)( a +3b) C .( a -3b( a +3b) D .(3a-4b)(4a+3b)
8.若∠A 和 ∠B 互为余角, ∠B 与 ∠C 互补,且∠C=130°,则∠A的度数为( B )
A .30° B .40° C.40 D .60°
9.有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示,右边场地为长方形,长为2( a + b ),则宽为( )
A .( a - b ) B . a - b C .( a + b ) D . a + b
10.如图所示的图形由一个大正方形 ABEF 、一个小正方形 ADGH 和一个长方形 ABCD 不重合无缝隙得拼接在一起,已知长方形 ABCD 的面积是6,正方形 ABEF 和正方形 ADGH 的面积之和为69,那么长方形 ABCD 的周长是( )
A .12 B .18 C .16 D .14
二、填空题:(每小题4分,共24分)
11.己知10m=4,10n=5,则10m+n= .
12.计算:-b2·(-b)2·(- b3)= .
13.若∠1与∠2是对顶角,且∠1+∠2=140°,则∠1的补角是 .
14.将一副三角板如图所示摆放,若∠BAE =126°,则 ∠CAD 的度数是 .
(第14题图) (第16题图)
15.已知 a + b =5,a2+b2=19,那么 ab 的值是 .
16.如图,以长方形 ABCD 的四条边为边向外作四个正方形,设计出"中"字图案,若四个正方形的周长之和为40,面积之和为26,则长方形 ABCD 的面积为 6 .
三.解答题:(共9小题,86分)
17.(每小题4分,共8分)计算
(1)(-3)2+(3-π)0+(-)-1 (2)(x +4)(2x-1)
18.(每小题4分,共8分)计算:
(1)a2·a4+(2a3)2 (2)(12x4-8x3)÷(2x)2
19.(每小题4分,共8分)利用整式乘法公式计算:
(1)399x401+1 (2).1032
20.(每小题6分,共12分)先化简,再求值:
(1)( x +1)2+( x +2)( x -3),其中 x =.
(2)已知2a2+3a-4=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值。
21、(6分)已知一个角的补角是这个角的余角的3倍,求这个角的度数.
22.(第(1)题6分,第(2)题4分,共10分)如图,某市有一块长为(3a+ b )米,宽为(2a+ b )米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像。
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当 a =3, b =2时的绿化面积.
23.(12分)阅读材料:如果一个数的平方等于﹣1,记为 i2 =-1,这个数i叫做虚数单位,那么形如 a + bi ( a, b 为实数)的数就叫做复数,a 叫这个复数的实部,b叫做这个复数的虚部.
4+4i+i2
它有如下特点:
①它的加,减,乘法运算与整式的加,减,乘法运算类似,例如计算:
(2+i)+(3-4i)=(2+3)+(1-4) i =5-3i,(3+ i ) i =3i+i2=3i-1.
②若两个复数,它们的实部和虚部分别相等,则称这两个复数相等;若它们的实部相等,虚
部互为相反数,则称这两个复数共轭;如1+2i的共轭复数为1-2i.
(1)(4分)填空:①(2+i)(2-i)= ; ②(2+i)2= .
(2)(4分)若 a + bi 是(1+2i)2的共轭复数,求(b - a )2的值;
(3)(4分)已知(a + i )(b + i )=1-3i,求(a2+b2) ( i +i2+i3+...+i2025)的值.
24.(10分)阅读下列材料:
若 x 满足(9- x )( x -4)=4,求(4- x )2+(x -9)2的值.
设9- x = a ,x -4= b ,则(9- x )( x -4)= ab =4,a + b =(9- x )+( x -4)=5
∴(4- x )2+( x -9)2=(9- x )2+( x -4)2=a2+b2=( a + b )2-2ab=52-2x4=17
请仿照上面的方法求解下面问题:
(1)(4分)若 x 满足(5- x)(x -2)=2,求(5-x )2+(x -2)2的值;
(2)已知正方形 ABCD 的边长为 x,E、F 分别是 AD、DC 上的点,且 AE =1,CF =3,长方形 EMFD 的面积是48,分别以MF 、DF 为边作正方形。
①(2分)MF = , DF = :(用含 x 的式子表示)
②(4分)求阴影部分的面积.
25.(12分)综合与探究
数学实践活动课上,"奋进"小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
【实践操作】三角尺中的数学
【问题发现】
(1)①(3分)填空:如图1,若∠ACB =145,则∠ACE 的度数是 ,∠DCB 的度数 ,∠ECD 的度数是 。
②(4分)如图1,你发现∠ACE 与 ∠DCB 的大小有何关系? ∠ACB 与 ∠ECD 的大小又有何关系?请直接写出你发现的结论.
【类比探究】
(2)(5分)如图2,当△ACD 与 △BCE 没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
答案
一、选择题:(每小题4分,共40分)
1.计算a2·a4结果正确的是( B )
A .a2 B .a6 C .a8 D .2a2
2.在科研人员的不懈努力下,我国成功制造出了"超薄钢",打破了日德垄断,据悉,该材料的厚度仅有0.000015米,将数据0.000015用科学记数法表示为( A )
A .1.5×10-5 B .1.5×10-4 C.15×10-4 D .0.15×10﹣6
3.下列运算正确的是( D )
A .3a- a =2a2 B . a3·a2 = a6 C .( ab )2=ab2 D .(-a3)2= a6
4.在下列图中,∠1与∠2属于对顶角的是( B )
5.如图, A , B , C , D 四点在直线上,点 M 在直线外,MC⊥l,若 MA =5cm, MB =4cm, MC=2cm, MD =3cm,则点 M 到直线l的距离是( C )
A.2cm B .3cm C .4cm D . 5cm
(第5题图) (第9题图) (第10题图)
6.下列多项式相乘,能用平方差公式计算的是( A )
A .(2a-3b)(3b+2a) B .(2a+ b )(2b- a ) C .(3m- n )(-3m+ n ) D .(m -n)(﹣n +m )
7.下列各式中,能用完全平方公式计算的是( B )
A .(2a-3b)(-2a-3b) B .( a +3b)( a +3b) C .( a -3b( a +3b) D .(3a-4b)(4a+3b)
8.若∠A 和 ∠B 互为余角, ∠B 与 ∠C 互补,且∠C=130°,则∠A的度数为( B )
A .30° B .40° C.40 D .60°
9.有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示,右边场地为长方形,长为2( a + b ),则宽为( C )
A .( a - b ) B . a - b C .( a + b ) D . a + b
10.如图所示的图形由一个大正方形 ABEF 、一个小正方形 ADGH 和一个长方形 ABCD 不重合无缝隙得拼接在一起,已知长方形 ABCD 的面积是6,正方形 ABEF 和正方形 ADGH 的面积之和为69,那么长方形 ABCD 的周长是( B )
A .12 B .18 C .16 D .14
二、填空题:(每小题4分,共24分)
11.己知10m=4,10n=5,则10m+n= 20 .
12.计算:-b2·(-b)2·(- b3)= b7 .
13.若∠1与∠2是对顶角,且∠1+∠2=140°,则∠1的补角是 110° .
14.将一副三角板如图所示摆放,若∠BAE =126°,则 ∠CAD 的度数是 54° .
(第14题图) (第16题图)
15.已知 a + b =5,a2+b2=19,那么 ab 的值是 3 .
16.如图,以长方形 ABCD 的四条边为边向外作四个正方形,设计出"中"字图案,若四个正方形的周长之和为40,面积之和为26,则长方形 ABCD 的面积为 6 .
三.解答题:(共9小题,86分)
17.(每小题4分,共8分)计算
(1)(-3)2+(3-π)0+(-)-1 (2)(x +4)(2x-1)
=9+1﹣2 =2x2﹣x+8x﹣4
=8 =2x2+7x﹣4
18.(每小题4分,共8分)计算:
(1)a2·a4+(2a3)2 (2)(12x4-8x3)÷(2x)2
=a6+4a6 =(12x4-8x3)÷(4x2)
=5a6 =3x2﹣2x
19.(每小题4分,共8分)利用整式乘法公式计算:
(1)399x401+1 (2).1032
=(400﹣1)(400+1)+1 =(100+3)2
=4002﹣1+1 =1002+×100×3+32
=160000 =10609
20.(每小题6分,共12分)先化简,再求值:
(1)( x +1)2+( x +2)( x -3),其中 x =.
解:原式=x2+2x+1+x2﹣3x+2x﹣6
=2x2+x﹣5
将x =代入得:2×+﹣5=﹣4
(2)已知2a2+3a-4=0,求代数式3a(2a+1)-(2a+1)(2a-1)的值。
解:原式=6a2+3a﹣4a2+1
=2a2+3a+1
将2a2+3a=4代入得4+1=5
21、(6分)已知一个角的补角是这个角的余角的3倍,求这个角的度数.
解设这个角为x,则
180°﹣x=3(90°﹣x)
解得 x=45°
答:这个角为45°
22.(第(1)题6分,第(2)题4分,共10分)如图,某市有一块长为(3a+ b )米,宽为(2a+ b )米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像。
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当 a =3, b =2时的绿化面积.
(3a+b)(2a+b)﹣(a+b)2
=6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2
=(5a2+3ab)平方米
(2)a =3, b =2代入得:5×32+3×3×2=63平方米
23.(12分)阅读材料:如果一个数的平方等于﹣1,记为 i2 =-1,这个数i叫做虚数单位,那么形如 a + bi ( a, b 为实数)的数就叫做复数,a 叫这个复数的实部,b叫做这个复数的虚部.
4+4i+i2
它有如下特点:
①它的加,减,乘法运算与整式的加,减,乘法运算类似,例如计算:
(2+i)+(3-4i)=(2+3)+(1-4) i =5-3i,(3+ i ) i =3i+i2=3i-1.
②若两个复数,它们的实部和虚部分别相等,则称这两个复数相等;若它们的实部相等,虚
部互为相反数,则称这两个复数共轭;如1+2i的共轭复数为1-2i.
(1)(4分)填空:①(2+i)(2-i)= ; ②(2+i)2= .
(2)(4分)若 a + bi 是(1+2i)2的共轭复数,求(b - a )2的值;
(3)(4分)已知(a + i )(b + i )=1-3i,求(a2+b2) ( i +i2+i3+...+i2025)的值.
(1)①5 ②3+4i
(2)(1+2i)2=1+4i﹣4=﹣3+4i
∵ a + bi 是(1+2i)2的共轭复数
∴a=﹣3,b=﹣4
(b - a )2=1
(3)(a + i )(b + i )=ab+ai+bi﹣1=ab﹣1+(a+b)i=1-3i
∴ab=2,a+b=﹣3
(a2+b2) ( i +i2+i3+...+i2025)
=(a2+b2)i
=5i
24.(10分)阅读下列材料:
若 x 满足(9- x )( x -4)=4,求(4- x )2+(x -9)2的值.
设9- x = a ,x -4= b ,则(9- x )( x -4)= ab =4,a + b =(9- x )+( x -4)=5
∴(4- x )2+( x -9)2=(9- x )2+( x -4)2=a2+b2=( a + b )2-2ab=52-2x4=17
请仿照上面的方法求解下面问题:
(1)(4分)若 x 满足(5- x)(x -2)=2,求(5-x )2+(x -2)2的值;
(2)已知正方形 ABCD 的边长为 x,E、F 分别是 AD、DC 上的点,且 AE =1,CF =3,长方形 EMFD 的面积是48,分别以MF 、DF 为边作正方形。
①(2分)MF = , DF = :(用含 x 的式子表示)
②(4分)求阴影部分的面积.
(1)设5- x = a , x -2= b .则(5- x )( x -2)= ab =2,a + b =5- x + x -2=3.
∴(5- x )2+( x -2)2=a2+b2=( a + b )2-2ab=32-2x2=9-4=5.
①∵正方形 ABCD 的边长为 x , AE =1, CF =3
∴MF = ED = AD - AE = x -1,DF = CD - CF = x -3.
②阴影部分面积等于以 MF 为边的正方形面积减去以 DF为边的正方形面积,即(x -1)2-( x -3)2
∵长方形 EMFD 的面积是48,( x -1)( x -3)=48.
设 x -1= a ,3- x = b
∴ab =-48,a + b = x -1+3- x =2
∴a- b = x -1+ x -3= MF + DF >0.
∴( x -1)2+( x -3)2=( x -1)2+(3- x )2=a2+b2=( a + b )2-2ab=22-2x(-48)=100.
∴( a - b )2=a2+b2-2ab=100-2x(-48)=196.
∵a + b >0
∴a - b =14.
∴( x -1)2-( x -3)2=( x -1)2-(3- x )2=a2-b2=( a + b )( a - b )=2×14=28.
25.(12分)综合与探究
数学实践活动课上,"奋进"小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点 C
【实践操作】三角尺中的数学
【问题发现】
(1)①(3分)填空:如图1,若∠ACB =145,则∠ACE 的度数是 ,∠DCB 的度数 ,∠ECD 的度数是 。
②(4分)如图1,你发现∠ACE 与 ∠DCB 的大小有何关系? ∠ACB 与 ∠ECD 的大小又有何关系?请直接写出你发现的结论.
【类比探究】
(2)(5分)如图2,当△ACD 与 △BCE 没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
①∠ACE =∠DCB =145°-90°=55° ,∠ECD =∠BCE -∠BCD =90°-55°=35°
②∠ACE = ∠DCB ,∠ACB + ∠ECD =180
(2)答:当△ACD 与△BCE 没有重合部分时,上述②中发现的结论依然成立.
理由:∵∠ACD =∠ECB =90°
∴∠ACD +∠ DCE =∠ ECB +∠ DCE
∴∠ACE =∠DCB
∵∠ACD = ∠ECB =90°
∴∠ACD + ∠ECB =180°
∵∠ACD +∠ECD +∠ECB +∠ACB =360°
∴∠ACB +∠ECD =180°
∴∠ACE =∠DCB , ∠ACB +∠ECD =180°
所以上述②中发现的结论依然成立.
同课章节目录
