3.1 不等式的意义 课件(共22张PPT)
文档属性
| 名称 | 3.1 不等式的意义 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 278.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 08:02:26 | ||
图片预览








文档简介
(共22张PPT)
不等式的意义
七年级下册 第三章 3.1
学习目标
1.理解不等式的意义,并根据给定条件列出不等式。
2.能够正确理解“非负数”、“不小于”等数学术语。
3.通过具体实例建立不等式模型的过程,增强符号感和数学化能力。
新课导入
什么是等式?
表示相等关系的式子。
特征:含“=”号。
思考:表示不等关系的式子叫做什么?它有什么特征?
不等式,含不等号
新知探究
小华的身高为155 cm,小楠的身高为156 cm,你可以用不等号“>”或“<”来表示他们身高之间的关系吗?
156>155或155<156.
新知探究
(1)在处于平衡状态的托盘天平的左盘放上一个网球、右盘放上一质量为20 g的砝码后,天平向左倾斜,如图所示,问网球的质量m g与砝码的质量20 g之间具有怎样的关系?
思考
(1)中存在不等量关系:网球的质量>砝码的质量,即m > 20.
新知探究
(2)一辆轿车在一条规定车速不低于60 km/h,且不高于100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间t(h)之间的关系呢?
思考
(2)中存在不等量关系:
高速公路上行驶的路程≥一直最低时速行驶的路程,即s≥ 60t,
高速公路上行驶的路程≤一直最低时速行驶的路程,即s≤ 100t.
新知探究
156>155,155<156,m>20,s≥60t,s≤100t有什么共同点?
抽象
左右两边不相等,用不等号进行连接
用不等号 (>,<,≥,≤,≠) 连接而成式子叫作不等式.
新知探究
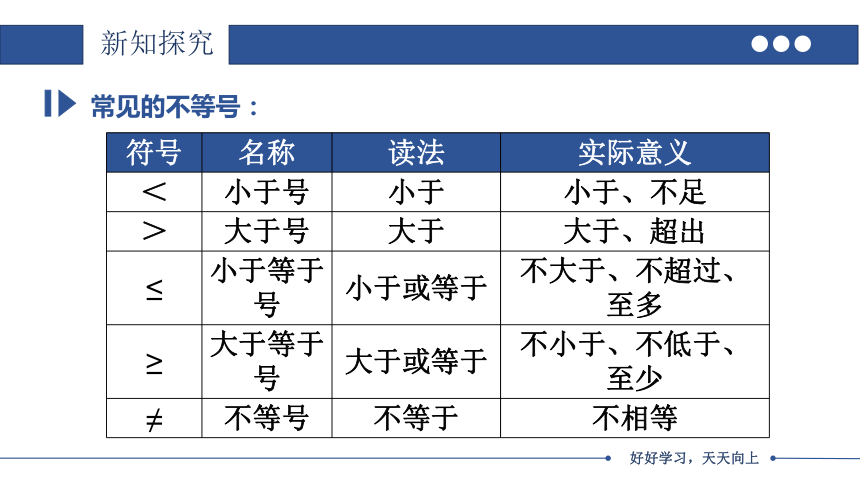
符号 名称 读法 实际意义
< 小于号 小于 小于、不足
> 大于号 大于 大于、超出
≤ 小于等于号 小于或等于 不大于、不超过、至多
≥ 大于等于号 大于或等于 不小于、不低于、至少
≠ 不等号 不等于 不相等
常见的不等号:
新知探究
下列式子:①3x+4<0;②y=3;③5x+3A.1个
B.2个
C.3个
D.4个
牛刀小试
B
例1 用不等式表示下列数量关系:
(1)a的5倍大于7;
(2)a与b的和的一半小于1;
(3)长、宽分别为b cm,c cm的长方形的面积小于边长为 a cm的正方形的面积.
例题探究
5a
>
5a>
<
1
<
新知探究
与不等号相关的关键词:
>:大于,高于,超过,正数……
≥:大于或等于,不小于,不低于,至少,非负数……
<:小于,低于,不足,负数……
≤:小于或等于,不大于,不高于,不超过,至多,非正数……
≠:不等于
已知一支圆珠笔的售价为1.5元,签字笔与圆珠笔相比每支贵2元. 小华带了50元,买了x支圆珠笔和10支签字笔.
例题探究
售价 所需购买支数 总价
圆珠笔
签字笔
1.5
3.5
x
10
1.5x
35
小华所需支付的金额为多少?
(1.5x+35)元
请用含x的不等式表示小华所需支付的金额与50元之间的关系.
1.5x+35≤50
例题探究
1.5x+35≤50是含有未知数x的不等式,表示x用哪些数代入,能够使得①式成立,即左边的多项式1.5x+35的值小于或等于右边的值50.
根据生活常识可知,①式中x只能取正整数,于是
若x取1,将其代入①式,得1.5×1+35=36.5<50
.……
思考:x能取哪些值?小华至多能买几支圆珠笔?
例题探究
若x取9,将其代入①式,得1.5×9+35=48.5<50.
若x取10,将其代入①式,得1.5×10+35=50.
若x取11,将其代入①式,得1.5×11+35=51.5≥50.
因此,小华至多能买10支圆珠笔.
例2中,如果小华带了60元钱,他至多能买多少支圆珠笔?
例题探究
做一做
解:由于小华只带了60元,因此他买x支圆珠笔和10支签字笔支付的金额不超过60元,则有以下不等量关系:
1.5x +35≤60.
若x取16,将其代入①式,得1.5×16+35=59<60.
若x取17,将其代入①式,得1.5×17+35=60.5>60.
因此,小华至多能买16支圆珠笔.
课堂小结
用不等号 (>,<,≥,≤,≠) 连接而成式子叫作不等式.
与不等号相关的关键词:
>:大于,高于,超过,正数……
≥:大于或等于,不小于,不低于,至少,非负数……
<:小于,低于,不足,负数……
≤:小于或等于,不大于,不高于,不超过,至多,非正数……
≠:不等于
课堂练习
1.若2x-y□5是不等式,则“□”内的符号不能是 ( )
A.+
B.>
C.≠
D.≤
A
课堂练习
2.某养生钙奶饮料的包装瓶上标注“每100 g内含钙≥150 mg”,它的含义是指( )
A. 每100 g内含钙量是150 mg
B. 每100 g内含钙量不低于150 mg
C. 每100 g内含钙量高于150 mg
D. 每100 g内含钙量不超过150 mg
B
课堂练习
3.小霞原有存款52元,小明原有存款70元.从这个月开始,小霞每月存15元零花钱,小明每月存12元零花钱,设经过n个月后小霞的存款超过小明,可列不等式为 ( )
A.52+15n>70+12n
B.52+15n<70+12n
C.52+12n>70+15n
D.52+12n<70+15n
A
课堂练习
4.用不等式表示下列数量关系:
(1)m与n的和是正数:________.
(2)x的2倍与y的一半的差是负数:________.
(3)3与a的和的一半不大于-1:_____________.
m+n>0
2x-y<0
(a+3)≤-1
课后作业
课堂作业:P58 T2
家庭作业:《学法》P36 A组(基础一般)
B组(基础较好)
C组(选做)
不等式的意义
七年级下册 第三章 3.1
学习目标
1.理解不等式的意义,并根据给定条件列出不等式。
2.能够正确理解“非负数”、“不小于”等数学术语。
3.通过具体实例建立不等式模型的过程,增强符号感和数学化能力。
新课导入
什么是等式?
表示相等关系的式子。
特征:含“=”号。
思考:表示不等关系的式子叫做什么?它有什么特征?
不等式,含不等号
新知探究
小华的身高为155 cm,小楠的身高为156 cm,你可以用不等号“>”或“<”来表示他们身高之间的关系吗?
156>155或155<156.
新知探究
(1)在处于平衡状态的托盘天平的左盘放上一个网球、右盘放上一质量为20 g的砝码后,天平向左倾斜,如图所示,问网球的质量m g与砝码的质量20 g之间具有怎样的关系?
思考
(1)中存在不等量关系:网球的质量>砝码的质量,即m > 20.
新知探究
(2)一辆轿车在一条规定车速不低于60 km/h,且不高于100 km/h的高速公路上行驶,如何用式子来表示轿车在该高速公路上行驶的路程s(km)与行驶时间t(h)之间的关系呢?
思考
(2)中存在不等量关系:
高速公路上行驶的路程≥一直最低时速行驶的路程,即s≥ 60t,
高速公路上行驶的路程≤一直最低时速行驶的路程,即s≤ 100t.
新知探究
156>155,155<156,m>20,s≥60t,s≤100t有什么共同点?
抽象
左右两边不相等,用不等号进行连接
用不等号 (>,<,≥,≤,≠) 连接而成式子叫作不等式.
新知探究
符号 名称 读法 实际意义
< 小于号 小于 小于、不足
> 大于号 大于 大于、超出
≤ 小于等于号 小于或等于 不大于、不超过、至多
≥ 大于等于号 大于或等于 不小于、不低于、至少
≠ 不等号 不等于 不相等
常见的不等号:
新知探究
下列式子:①3x+4<0;②y=3;③5x+3
B.2个
C.3个
D.4个
牛刀小试
B
例1 用不等式表示下列数量关系:
(1)a的5倍大于7;
(2)a与b的和的一半小于1;
(3)长、宽分别为b cm,c cm的长方形的面积小于边长为 a cm的正方形的面积.
例题探究
5a
>
5a>
<
1
<
新知探究
与不等号相关的关键词:
>:大于,高于,超过,正数……
≥:大于或等于,不小于,不低于,至少,非负数……
<:小于,低于,不足,负数……
≤:小于或等于,不大于,不高于,不超过,至多,非正数……
≠:不等于
已知一支圆珠笔的售价为1.5元,签字笔与圆珠笔相比每支贵2元. 小华带了50元,买了x支圆珠笔和10支签字笔.
例题探究
售价 所需购买支数 总价
圆珠笔
签字笔
1.5
3.5
x
10
1.5x
35
小华所需支付的金额为多少?
(1.5x+35)元
请用含x的不等式表示小华所需支付的金额与50元之间的关系.
1.5x+35≤50
例题探究
1.5x+35≤50是含有未知数x的不等式,表示x用哪些数代入,能够使得①式成立,即左边的多项式1.5x+35的值小于或等于右边的值50.
根据生活常识可知,①式中x只能取正整数,于是
若x取1,将其代入①式,得1.5×1+35=36.5<50
.……
思考:x能取哪些值?小华至多能买几支圆珠笔?
例题探究
若x取9,将其代入①式,得1.5×9+35=48.5<50.
若x取10,将其代入①式,得1.5×10+35=50.
若x取11,将其代入①式,得1.5×11+35=51.5≥50.
因此,小华至多能买10支圆珠笔.
例2中,如果小华带了60元钱,他至多能买多少支圆珠笔?
例题探究
做一做
解:由于小华只带了60元,因此他买x支圆珠笔和10支签字笔支付的金额不超过60元,则有以下不等量关系:
1.5x +35≤60.
若x取16,将其代入①式,得1.5×16+35=59<60.
若x取17,将其代入①式,得1.5×17+35=60.5>60.
因此,小华至多能买16支圆珠笔.
课堂小结
用不等号 (>,<,≥,≤,≠) 连接而成式子叫作不等式.
与不等号相关的关键词:
>:大于,高于,超过,正数……
≥:大于或等于,不小于,不低于,至少,非负数……
<:小于,低于,不足,负数……
≤:小于或等于,不大于,不高于,不超过,至多,非正数……
≠:不等于
课堂练习
1.若2x-y□5是不等式,则“□”内的符号不能是 ( )
A.+
B.>
C.≠
D.≤
A
课堂练习
2.某养生钙奶饮料的包装瓶上标注“每100 g内含钙≥150 mg”,它的含义是指( )
A. 每100 g内含钙量是150 mg
B. 每100 g内含钙量不低于150 mg
C. 每100 g内含钙量高于150 mg
D. 每100 g内含钙量不超过150 mg
B
课堂练习
3.小霞原有存款52元,小明原有存款70元.从这个月开始,小霞每月存15元零花钱,小明每月存12元零花钱,设经过n个月后小霞的存款超过小明,可列不等式为 ( )
A.52+15n>70+12n
B.52+15n<70+12n
C.52+12n>70+15n
D.52+12n<70+15n
A
课堂练习
4.用不等式表示下列数量关系:
(1)m与n的和是正数:________.
(2)x的2倍与y的一半的差是负数:________.
(3)3与a的和的一半不大于-1:_____________.
m+n>0
2x-y<0
(a+3)≤-1
课后作业
课堂作业:P58 T2
家庭作业:《学法》P36 A组(基础一般)
B组(基础较好)
C组(选做)
同课章节目录
