苏科版2024—2025学年八年级下册数学第一次月考模拟试卷A卷(含解析)
文档属性
| 名称 | 苏科版2024—2025学年八年级下册数学第一次月考模拟试卷A卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 964.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏科版2024—2025学年八年级下册数学第一次月考模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.一个不透明的盒子中装有1白球和200个黑球,它们除了颜色外都相同,将球搅匀,从中任意摸出一个球,摸到黑球是( )
A.必然事件 B.随机事件 C.不可能事件 D.以上事件都有可能
3.下列调查中,最适宜采用全面调查(普查)的是( )
A.调查一批灯泡的使用寿命 B.调查淮河水质情况
C.调查江苏电视台某栏目的收视率 D.调查全班同学的身高
4.下列叙述错误的是( )
A.平行四边形的对角线互相平分 B.菱形的对角线互相平分
C.菱形的对角线相等 D.矩形的对角线相等
5.如图,菱形ABCD的对角线交于原点O,若点B的坐标为(4,m),点D的坐标为(n,2),则m+n的值为( )
A.2 B.﹣2 C.6 D.﹣6
6.下面性质中菱形有而矩形没有的是( )
A.邻角互补 B.内角和为360°
C.对角线相等 D.对角线互相垂直
7.如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的长度为( )
A.10 B.5 C.2.5 D.2.25
8.顺次连接四边形四条边的中点,所得的四边形是矩形,则原四边形一定是( )
A.平行四边形 B.对角线相等的四边形
C.对角线互相垂直的四边形 D.矩形
9.如图,四边形ABCD为菱形,对角线AC,BD交于点O,DE⊥AB,垂足为E.若AB=5,BD=6,则DE的长是( )
A. B. C. D.
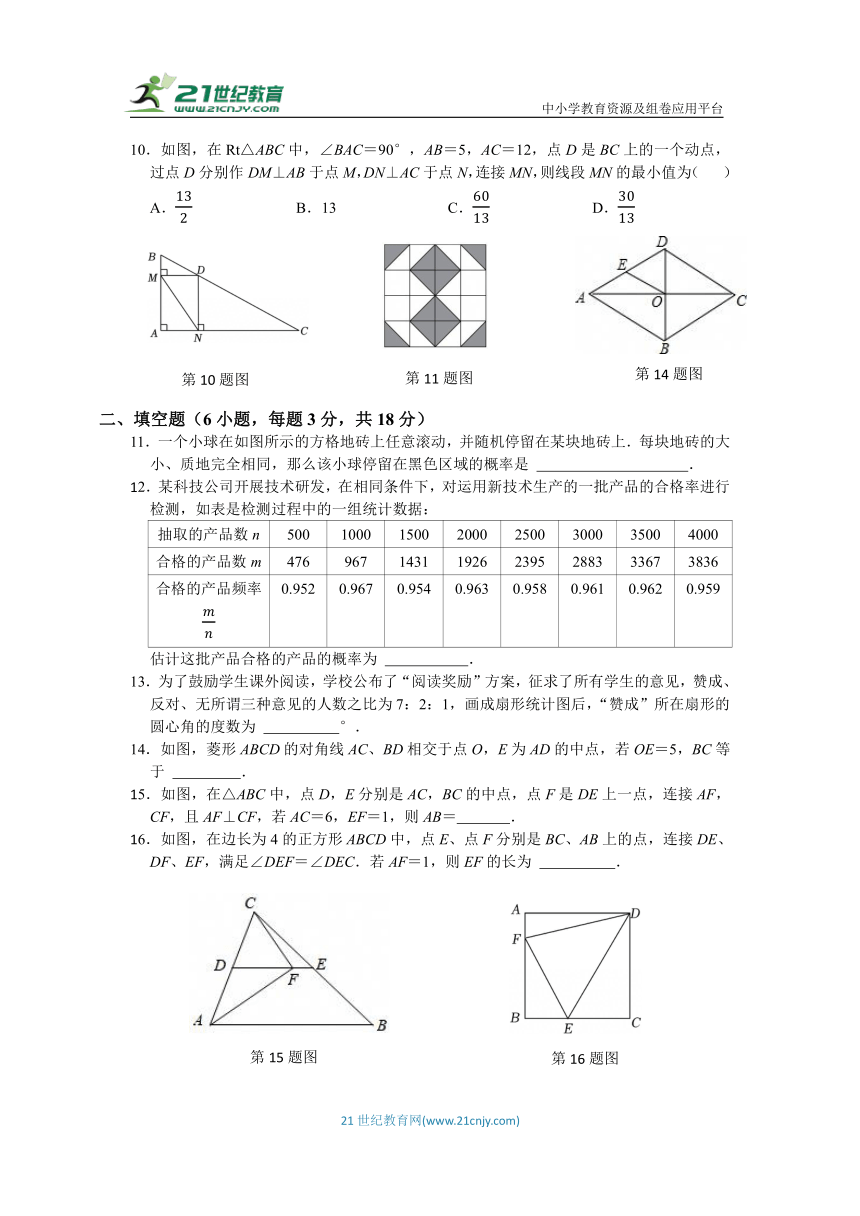
10.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,点D是BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为( )
A. B.13 C. D.
二、填空题(6小题,每题3分,共18分)
11.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
12.某科技公司开展技术研发,在相同条件下,对运用新技术生产的一批产品的合格率进行检测,如表是检测过程中的一组统计数据:
抽取的产品数n 500 1000 1500 2000 2500 3000 3500 4000
合格的产品数m 476 967 1431 1926 2395 2883 3367 3836
合格的产品频率 0.952 0.967 0.954 0.963 0.958 0.961 0.962 0.959
估计这批产品合格的产品的概率为 .
13.为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,征求了所有学生的意见,赞成、反对、无所谓三种意见的人数之比为7:2:1,画成扇形统计图后,“赞成”所在扇形的圆心角的度数为 °.
14.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=5,BC等于 .
15.如图,在△ABC中,点D,E分别是AC,BC的中点,点F是DE上一点,连接AF,CF,且AF⊥CF,若AC=6,EF=1,则AB= .
16.如图,在边长为4的正方形ABCD中,点E、点F分别是BC、AB上的点,连接DE、DF、EF,满足∠DEF=∠DEC.若AF=1,则EF的长为 .
第II卷
苏科版2024—2025学年八年级下册数学第一次月考模拟试卷A卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
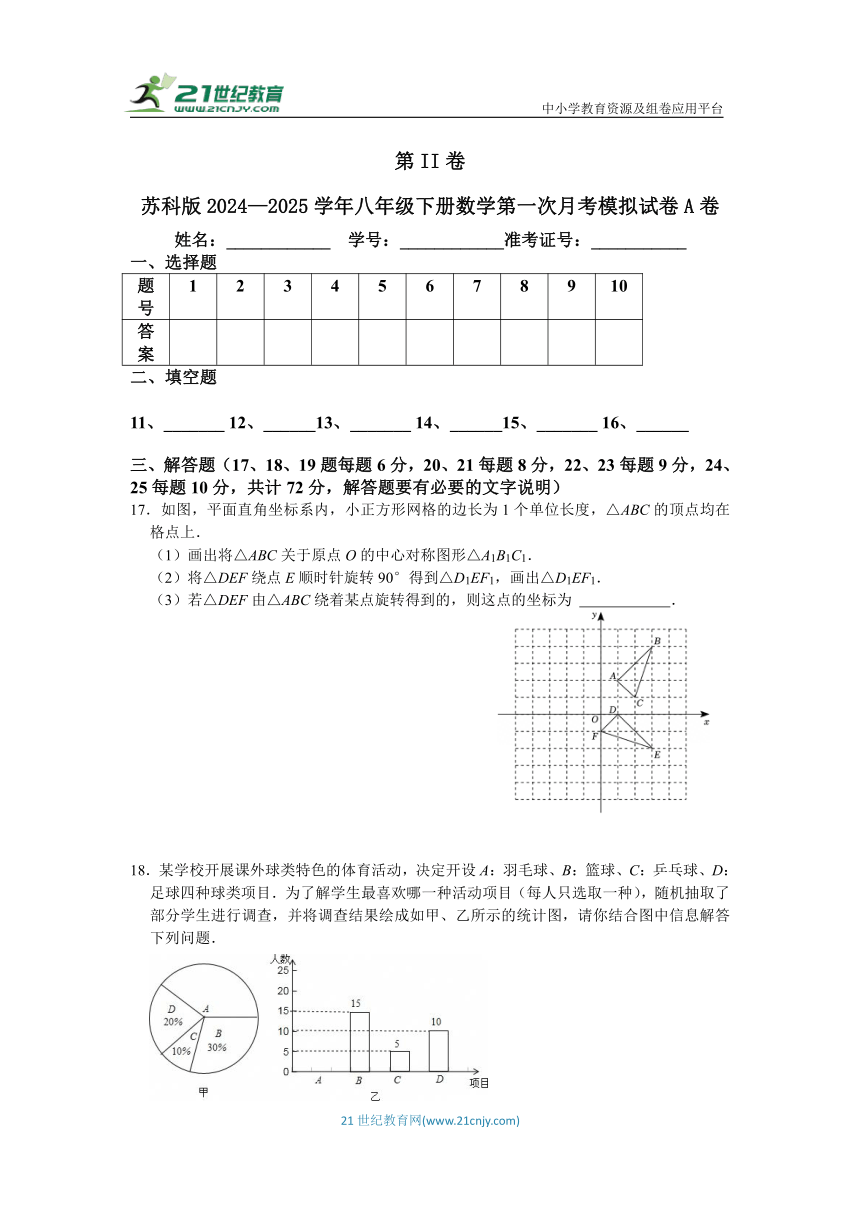
17.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点均在格点上.
(1)画出将△ABC关于原点O的中心对称图形△A1B1C1.
(2)将△DEF绕点E顺时针旋转90°得到△D1EF1,画出△D1EF1.
(3)若△DEF由△ABC绕着某点旋转得到的,则这点的坐标为 .
18.某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?
19.在一个不透明的盒子里装有红、黑两种颜色的球共20个,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,我们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到如表中的一组统计数据:
摸球的次数n 50 100 300 500 800 1000 2000
摸到红球的次数m 14 33 95 155 241 298 602
摸到红球的频率 0.28 0.33 0.317 0.31 0.301 0.298 0.301
(1)通过以上实验,盒子里红球的数量为 个.
(2)若先从袋子中取出x(x>1)个红球,再从袋子中随机摸出1个球,若“摸出黑球”为必然事件,则x= .
(3)若先从袋子中取出x个红球,再放入x个一样的黑球并摇匀,随机摸出1个红球的概率为,求x的值.
20.如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE=DA,连接AE.
(1)求证:AE=BC;
(2)若AB=6,CD=2,求四边形ABCE的面积.
21.如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.
22.如图,在矩形纸片ABCD中,AB=6,BC=8,将矩形纸片折叠,使点B与点D重合,点A落在点E处,FG是折痕,连接BF.
(1)求证:四边形BGDF是菱形;
(2)求折痕FG的长.
23.如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其折叠,使点D与点B重合.
(1)求证:BE=BF;
(2)求折叠后DE的长;
(3)求以折痕EF为边的正方形面积.
24.如图所示,菱形ABCD的顶点A,B在x轴上,点A在点B的左侧,点D在y轴的正半轴上.点C的坐标为(4,2).动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.
(1)①点B的坐标 .
②求菱形ABCD的面积;
(2)当t=3时,问线段AC上是否存在点E,使得PE+DE最小,如果存在,求出PE+DE最小值;如果不存在,请说明理由;
(3)若点P到AC的距离是1,则点P运动的时间t等于 .
25.如图,四边形ABCD为矩形,A(0,0),B(4,0),D(0,8),将矩形ABCD沿直线DB折叠,使点A落在点A′处.
(1)求证:DE=BE;
(2)求直线DE的函数表达式;
(3)在y轴上作点F(0,1),连接EF,点N是x轴上一动点,直线DE上是否存在点M,使以M,N,E,F为顶点的四边形是平行四边形?若存在,直接写出M点坐标;若不存在,说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C D D C C C C
1.【解答】解:A.既是中心对称图形,又是轴对称图形,符合题意;
B.不是中心对称图形,是轴对称图形,不符合题意;
C.是中心对称图形,不是轴对称图形,不符合题意;
D.是轴对称图形,不是中心对称图形,不符合题意;
故选:A.
2【解答】解:一个不透明的盒子中装有1白球和200个黑球,它们除了颜色外都相同,将球搅匀,从中任意摸出一个球,
可能摸到白球,有可能摸到黑球,因此是随机事件,
故选:B.
3.【解答】解:A、调查一批灯泡的使用寿命,具有破坏性,应当使用抽样调查,故本选项不合题意;
B、调查淮河水质,水量较大,应当采用抽样调查的方式,故本选项不合题意;
C、调查江苏电视台某栏目的收视率,应当采用抽样调查的方式,故本选项不合题意.
D、调查全班同学的身高,应当采用全面调查,故本选项符合题意.
故选:D.
4.【解答】解:A、正确.平行四边形的对角线互相平分.
B、正确.菱形的对角线互相平分.
C、错误.菱形的对角线垂直且互相平分,不一定相等.
D、正确.矩形的对角线相等.
故选:C.
5.【解答】解:∵菱形ABCD的对角线交于原点O,点B的坐标为(4,m),点D的坐标为(n,2),
∴0,0,
解得n=﹣4,m=﹣2,
∴m+n=﹣2+(﹣4)=﹣6,
故选:D.
6.【解答】解:A、∵平行四边形的邻角互补,
∴矩形的邻角互补.故矩形和菱形的邻角均互补,故A错;
B、平行四边形的内角和为360,矩形内角和为360度.故矩形和菱形的内角和都是360°,故B错;
C、矩形的对角线相等,菱形的对角线互相垂直且平分,故C错;
D、菱形对角线互相垂直,矩形的对角线不互相垂直.
故选:D.
7.【解答】解:∵四边形ABCD是矩形,
∴AC=BD=10,BO=DOBD,
∴DOBD=5,
∵点P、Q是AO,AD的中点,
∴PQ是△AOD的中位线,
∴PQDO=2.5,
故选:C.
8.【解答】解:如图,连接AC、BD.
∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD,
故原图形一定是:对角线垂直的四边形.
故选:C.
9.【解答】解:∵四边形ABCD为菱形,BD=6,
∴OB=OD=3,OA=OC,AC⊥BD,
∴OA4,
∴AC=2OA=8,
∵DE⊥AB,
∴S菱形ABCD=AB DEAC BD8×6=24,
∴5DE=24,
∴DE,
故选:C.
10.【解答】解:∵∠BAC=90°,且BA=5,AC=12,
∴BC13,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积AB×ACBC×AD,
∴AD,
∴MN的最小值为;
故选:C.
二、填空题
11.【解答】解:若将每个小正方形的面积记为1,则大正方形的面积为16,其中阴影部分的面积为6,
所以该小球停留在黑色区域的概率是,
故答案为:.
12.【解答】解:由图表可知合格的产品频率都在0.95左右浮动,所以可估计这批产品合格的产品的概率为0.96,
故答案为:0.96.
13.【解答】解:“赞成”所在扇形的圆心角的度数为:360°252°,
故答案为:252.
14.【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△AOD为直角三角形.
∵OE=5,
∵点E为线段AD的中点,
∴AD=2OE=10,
∴BC=10.
故答案为:10.
15.【解答】解:在Rt△AFC中,点D是AC的中点,AC=6,
∴DFAC6=3,
∵EF=1,
∴DE=DF+EF=3+1=4,
∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=2×4=8,
故答案为:8.
16.【解答】解:如图,在EF上截取EG=EC,连接DG,
∵四边形ABCD是正方形,
∴∠A=∠C=90°,AB=BC=AD=CD=4,
在△DCE和△DGE中,
,
∴△DCE≌△DGE(SAS),
∴∠DGE=∠C=90°,DG=DC,
∵∠A=∠C=90°,AB=BC=4,
∴∠DGF=∠A=90°,DG=DA,
在Rt△DAF和Rt△DGF中,
,
∴Rt△DAF≌Rt△DGF(HL),
∴AF=GF=1,
∵EG=EC,
∴BE=BC﹣EC=4﹣EG,EF=EG+FG=EG+1,BF=AB﹣AF=4﹣1=3,
在Rt△BEF中,根据勾股定理,得BE2+BF2=EF2,
∴(4﹣EG)2+32=(EG+1)2,
解得EG=2.4,
∴EF=EG+FG=2.4+1=3.4,
∴EF的长为3.4.
故答案为:3.4.
三、解答题
17.【解答】解:(1)如图,△A1B1C1即为所求;
;
(2)如图,△D1EF1即为所求;
(3)根据旋转的性质可得,旋转中心为AD和CF垂直平分线的交点,图中点P即为旋转中心,
∴P(0,1),
故答案为:(0,1).
18.【解答】解:(1)样本中最喜欢A项目的人数所占的百分比为1﹣30%﹣10%﹣20%=40%,
其所在扇形统计图中对应的圆心角度数是360°×40%=144,
故答案为:40%,144;
(2)本次抽查的学生人数是:15÷30%=50(人),
∴喜欢A:篮球的人数是:50﹣15﹣5﹣10=20(人),
作图如下:
(3)3000×20%=600人,
答:根据样本估计全校最喜欢足球的学生人数约是600人.
19.【解答】解:(1)通过以上实验,摸到红球的概率估计为0.3,
盒子里红球的数量为:20×0.3=6(个).
故答案为:6;
(2)∵盒子里有6个红球,“摸出黑球”为必然事件,
∴x=6.
故答案为:6;
(3)由(1)知红球6个,黑球14个,根据题意得:
,
解得:x=1,
则x的值为1.
20.【解答】(1)证明:∵AD⊥CD及DE=AD
∴∠E=45°,
∵AB∥CD,
∴∠EAB+∠E=180°,
∴∠EAB=180°﹣∠E=135°,
∵∠B=45°,
∴∠EAB+∠B=180°,
∴AE∥BC,
∴四边形ABCE平行四边形,
∴AE=BC;
(2)解:∵四边形ABCE平行四边形,
∴CE=AB=6,
∴AD=DE=CE﹣CD=4,
∴四边形ABCE的面积为:AB AD=6×4=24.
21.【解答】(1)证明:
∵CE∥BD,DE∥AC,
∴四边形CODE为平行四边形,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠COD=90°,
∴平行四边形CODE是矩形;
(2)解:
∵四边形ABCD为菱形,
∴AO=OCAC6=3,OD=OB,∠AOB=90°,
在Rt△AOB中,由勾股定理得BO2=AB2﹣AO2,
∴BO4,
∴DO=BO=4,
∴四边形CODE的周长=2×(3+4)=14.
22.【解答】(1)证明:∵将矩形纸片折叠,使点B与点D重合,点A落在点E处,FG是折痕,
∴BF=DF,BG=DG,∠BFG=∠DFG,
∵四边形ABCD是矩形,
∴AD=BC=8,AD∥BC,
∴∠DFG=∠BGF,
∴∠BFG=∠BGF,
∴BF=BG,
∴BF=DF=BG=DG,
∴四边形BGDF是菱形;
(2)解:过F作FM⊥BC于M,则∠FMC=∠FMB=90°,
∵四边形ABCD是矩形,
∴∠A=∠ABM=90°,
∴四边形ABMF是矩形,
∴AB=FM=6,AF=BM,
设AF=x,则BF=DF=8﹣x,
在Rt△BAF中,由勾股定理得:AB2+AF2=BF2,
即62+x2=(8﹣x)2,
解得:x,
即AF,BG=8﹣x,
∴MG=BG﹣BM,
在Rt△FMG中,由勾股定理得:FG.
23.【解答】解:(1)在长方形ABCD中,AD∥BC
∴∠DEF=∠EFB.
∵∠DEF=∠BEF,
∴∠EFB=∠BEF,
∴BE=BF;
(2)设DE=xcm,则BE=xcm,AE=(8﹣x)cm,
在Rt△ABE中,由勾股定理42+(8﹣x) 2=x2,
∴x=5,即DE的长为5cm.
(3)过E作EH⊥BF于点H,
∵EH=AB=4,BH=AE=3
∴HF=BF﹣BH=5﹣3=2,
∴EF2=22+42=20,
∴以EF为边长的正方形的面积为20cm2.
24.【解答】解:(1)①∵C(4,2),∠AOD=90°,
∴DC=AD=4,DO=2,
∴OA2,
∵四边形ABCD为菱形,
∴AB=AD=4.
∴OB=AB﹣OA=2.
∴B(2,0).
故答案为:(2,0).
②∵在菱形ABCD中,DC=AB=4,OD=2,
∴菱形ABCD的面积=AB OD=4×28.
(2)如图1所示:
在菱形ABCD中,点P关于AC的对称点为P',AP'=3,
连接DP'交AC于点E,连接PE,
∴PE+DE=P'E+ED=P'D.
∵OA=2,OD=2,
∴OP'=1,
在Rt△DOP'中,
∵DO2+P'O2=P'D2,
∴.
∴PE+DE的最小值为.
(3)如图2所示:①当点P在AD上时,过点P作PE⊥AC,垂足为E.
由菱形的性质可知:∠PAE∠DAB=30°,
∵PE=1,∠PAE=30°,∠PEA=90°,
∴AP=2.
∴t=2.
②当点P在DC上时,如图3所示:
由菱形的性质可知:∠PCE∠DCB=30°,
∵PE=1,∠PCE=30°,∠PEC=90°,
∴CP=2.
∴AD+DP=4+2=6.
∴t=6.
③如图4所示:当点P在BC上时.
由菱形的性质可知:∠PCE∠DCB=30°,
∵PE=1,∠PCE=30°,∠PEC=90°,
∴CP=2.
∴AD+DC+CP=4+4+2=10.
∴t=10.
④如图5所示;点P在AB上时.
由菱形的性质可知:∠PAE∠DAB=30°,
∵PE=1,∠PAE=30°,∠PEA=90°,
∴AP=2.
∴AD+DC+BC+BP=4+4+4+2=14.
∴t=14.
综上所述,当t=2或t=6或t=10或t=14时,点P到AC的距离是1.
故答案为:2,6,10,14.
25.【解答】解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
由折叠可得:∠ADB=∠A′DB,
∴∠CBD=∠A′DB,
∴DE=BE.
(2)∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∵A(0,0),B(4,0),D(0,8),
∴C(4,8),
∴CD=4,BC=8,
由(1)知,DE=BE,
∴CE=BC﹣BE=BC﹣DE=8﹣DE,
在Rt△CDE中,DE2﹣CE2=CD2,
∴DE2﹣(8﹣DE)2=16,解得:DE=5,
∴BE=DE=5,
∵点E在BC上,
∴E(4,5),
设直线DE的解析式为y=kx+8,
∴4k+8=5,
∴,
∴直线DE的解析式为.
(3)∵以M,N,E,F为顶点的四边形是平行四边形,
∴①当EF为对角线时,MN于EF互相平分,
∴MN的中点也是EF的中点,
由(2)知,E(4,5),
∵F(0,1),
∴EF的中点坐标为E(2,3),
设,N(n,0),
∴m+n=4,,
∴,,
∴,;
②当EF为边时,
a.EM,FN为对角线时,EF∥MN,EM∥FN,
由(2)知,直线DE的解析式为,
∵点F(0,1)
∴直线FN的解析式为,
∴,
∵E(4,5),F(0,1),
根据待定系数法可得:直线EF的解析式为y=x+1,
∵EF∥MN,
∴直线MN的解析式为y=x,
联立,解得:,
∴M(,4);
②FN,EM为对角线时,FN的中点,也是EM的中点,
∴FN的中点在直线DE上,
设N(a,0),
∵F(0,1),
∴FN的中点坐标为,
∵直线DE的解析式为,
∴,
∴a=20,
∴FN的中点坐标为,
设,
∵E(4,5),
∴b+4=2×10,解得:b=16,
∴M(16,﹣4),
∴满足条件的点,(,4),(16,﹣4).
21世纪教育网(www.21cnjy.com)
苏科版2024—2025学年八年级下册数学第一次月考模拟试卷A卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.剪纸文化是中国最古老的民间艺术之一,下列剪纸图案中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.一个不透明的盒子中装有1白球和200个黑球,它们除了颜色外都相同,将球搅匀,从中任意摸出一个球,摸到黑球是( )
A.必然事件 B.随机事件 C.不可能事件 D.以上事件都有可能
3.下列调查中,最适宜采用全面调查(普查)的是( )
A.调查一批灯泡的使用寿命 B.调查淮河水质情况
C.调查江苏电视台某栏目的收视率 D.调查全班同学的身高
4.下列叙述错误的是( )
A.平行四边形的对角线互相平分 B.菱形的对角线互相平分
C.菱形的对角线相等 D.矩形的对角线相等
5.如图,菱形ABCD的对角线交于原点O,若点B的坐标为(4,m),点D的坐标为(n,2),则m+n的值为( )
A.2 B.﹣2 C.6 D.﹣6
6.下面性质中菱形有而矩形没有的是( )
A.邻角互补 B.内角和为360°
C.对角线相等 D.对角线互相垂直
7.如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的长度为( )
A.10 B.5 C.2.5 D.2.25
8.顺次连接四边形四条边的中点,所得的四边形是矩形,则原四边形一定是( )
A.平行四边形 B.对角线相等的四边形
C.对角线互相垂直的四边形 D.矩形
9.如图,四边形ABCD为菱形,对角线AC,BD交于点O,DE⊥AB,垂足为E.若AB=5,BD=6,则DE的长是( )
A. B. C. D.
10.如图,在Rt△ABC中,∠BAC=90°,AB=5,AC=12,点D是BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为( )
A. B.13 C. D.
二、填空题(6小题,每题3分,共18分)
11.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
12.某科技公司开展技术研发,在相同条件下,对运用新技术生产的一批产品的合格率进行检测,如表是检测过程中的一组统计数据:
抽取的产品数n 500 1000 1500 2000 2500 3000 3500 4000
合格的产品数m 476 967 1431 1926 2395 2883 3367 3836
合格的产品频率 0.952 0.967 0.954 0.963 0.958 0.961 0.962 0.959
估计这批产品合格的产品的概率为 .
13.为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,征求了所有学生的意见,赞成、反对、无所谓三种意见的人数之比为7:2:1,画成扇形统计图后,“赞成”所在扇形的圆心角的度数为 °.
14.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=5,BC等于 .
15.如图,在△ABC中,点D,E分别是AC,BC的中点,点F是DE上一点,连接AF,CF,且AF⊥CF,若AC=6,EF=1,则AB= .
16.如图,在边长为4的正方形ABCD中,点E、点F分别是BC、AB上的点,连接DE、DF、EF,满足∠DEF=∠DEC.若AF=1,则EF的长为 .
第II卷
苏科版2024—2025学年八年级下册数学第一次月考模拟试卷A卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点均在格点上.
(1)画出将△ABC关于原点O的中心对称图形△A1B1C1.
(2)将△DEF绕点E顺时针旋转90°得到△D1EF1,画出△D1EF1.
(3)若△DEF由△ABC绕着某点旋转得到的,则这点的坐标为 .
18.某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?
19.在一个不透明的盒子里装有红、黑两种颜色的球共20个,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,我们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到如表中的一组统计数据:
摸球的次数n 50 100 300 500 800 1000 2000
摸到红球的次数m 14 33 95 155 241 298 602
摸到红球的频率 0.28 0.33 0.317 0.31 0.301 0.298 0.301
(1)通过以上实验,盒子里红球的数量为 个.
(2)若先从袋子中取出x(x>1)个红球,再从袋子中随机摸出1个球,若“摸出黑球”为必然事件,则x= .
(3)若先从袋子中取出x个红球,再放入x个一样的黑球并摇匀,随机摸出1个红球的概率为,求x的值.
20.如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE=DA,连接AE.
(1)求证:AE=BC;
(2)若AB=6,CD=2,求四边形ABCE的面积.
21.如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.
22.如图,在矩形纸片ABCD中,AB=6,BC=8,将矩形纸片折叠,使点B与点D重合,点A落在点E处,FG是折痕,连接BF.
(1)求证:四边形BGDF是菱形;
(2)求折痕FG的长.
23.如图所示,长方形纸片ABCD的长AD=8cm,宽AB=4cm,将其折叠,使点D与点B重合.
(1)求证:BE=BF;
(2)求折叠后DE的长;
(3)求以折痕EF为边的正方形面积.
24.如图所示,菱形ABCD的顶点A,B在x轴上,点A在点B的左侧,点D在y轴的正半轴上.点C的坐标为(4,2).动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.
(1)①点B的坐标 .
②求菱形ABCD的面积;
(2)当t=3时,问线段AC上是否存在点E,使得PE+DE最小,如果存在,求出PE+DE最小值;如果不存在,请说明理由;
(3)若点P到AC的距离是1,则点P运动的时间t等于 .
25.如图,四边形ABCD为矩形,A(0,0),B(4,0),D(0,8),将矩形ABCD沿直线DB折叠,使点A落在点A′处.
(1)求证:DE=BE;
(2)求直线DE的函数表达式;
(3)在y轴上作点F(0,1),连接EF,点N是x轴上一动点,直线DE上是否存在点M,使以M,N,E,F为顶点的四边形是平行四边形?若存在,直接写出M点坐标;若不存在,说明理由.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C D D C C C C
1.【解答】解:A.既是中心对称图形,又是轴对称图形,符合题意;
B.不是中心对称图形,是轴对称图形,不符合题意;
C.是中心对称图形,不是轴对称图形,不符合题意;
D.是轴对称图形,不是中心对称图形,不符合题意;
故选:A.
2【解答】解:一个不透明的盒子中装有1白球和200个黑球,它们除了颜色外都相同,将球搅匀,从中任意摸出一个球,
可能摸到白球,有可能摸到黑球,因此是随机事件,
故选:B.
3.【解答】解:A、调查一批灯泡的使用寿命,具有破坏性,应当使用抽样调查,故本选项不合题意;
B、调查淮河水质,水量较大,应当采用抽样调查的方式,故本选项不合题意;
C、调查江苏电视台某栏目的收视率,应当采用抽样调查的方式,故本选项不合题意.
D、调查全班同学的身高,应当采用全面调查,故本选项符合题意.
故选:D.
4.【解答】解:A、正确.平行四边形的对角线互相平分.
B、正确.菱形的对角线互相平分.
C、错误.菱形的对角线垂直且互相平分,不一定相等.
D、正确.矩形的对角线相等.
故选:C.
5.【解答】解:∵菱形ABCD的对角线交于原点O,点B的坐标为(4,m),点D的坐标为(n,2),
∴0,0,
解得n=﹣4,m=﹣2,
∴m+n=﹣2+(﹣4)=﹣6,
故选:D.
6.【解答】解:A、∵平行四边形的邻角互补,
∴矩形的邻角互补.故矩形和菱形的邻角均互补,故A错;
B、平行四边形的内角和为360,矩形内角和为360度.故矩形和菱形的内角和都是360°,故B错;
C、矩形的对角线相等,菱形的对角线互相垂直且平分,故C错;
D、菱形对角线互相垂直,矩形的对角线不互相垂直.
故选:D.
7.【解答】解:∵四边形ABCD是矩形,
∴AC=BD=10,BO=DOBD,
∴DOBD=5,
∵点P、Q是AO,AD的中点,
∴PQ是△AOD的中位线,
∴PQDO=2.5,
故选:C.
8.【解答】解:如图,连接AC、BD.
∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
即AC⊥BD,
故原图形一定是:对角线垂直的四边形.
故选:C.
9.【解答】解:∵四边形ABCD为菱形,BD=6,
∴OB=OD=3,OA=OC,AC⊥BD,
∴OA4,
∴AC=2OA=8,
∵DE⊥AB,
∴S菱形ABCD=AB DEAC BD8×6=24,
∴5DE=24,
∴DE,
故选:C.
10.【解答】解:∵∠BAC=90°,且BA=5,AC=12,
∴BC13,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积AB×ACBC×AD,
∴AD,
∴MN的最小值为;
故选:C.
二、填空题
11.【解答】解:若将每个小正方形的面积记为1,则大正方形的面积为16,其中阴影部分的面积为6,
所以该小球停留在黑色区域的概率是,
故答案为:.
12.【解答】解:由图表可知合格的产品频率都在0.95左右浮动,所以可估计这批产品合格的产品的概率为0.96,
故答案为:0.96.
13.【解答】解:“赞成”所在扇形的圆心角的度数为:360°252°,
故答案为:252.
14.【解答】解:∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△AOD为直角三角形.
∵OE=5,
∵点E为线段AD的中点,
∴AD=2OE=10,
∴BC=10.
故答案为:10.
15.【解答】解:在Rt△AFC中,点D是AC的中点,AC=6,
∴DFAC6=3,
∵EF=1,
∴DE=DF+EF=3+1=4,
∵点D,E分别是AC,BC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=2×4=8,
故答案为:8.
16.【解答】解:如图,在EF上截取EG=EC,连接DG,
∵四边形ABCD是正方形,
∴∠A=∠C=90°,AB=BC=AD=CD=4,
在△DCE和△DGE中,
,
∴△DCE≌△DGE(SAS),
∴∠DGE=∠C=90°,DG=DC,
∵∠A=∠C=90°,AB=BC=4,
∴∠DGF=∠A=90°,DG=DA,
在Rt△DAF和Rt△DGF中,
,
∴Rt△DAF≌Rt△DGF(HL),
∴AF=GF=1,
∵EG=EC,
∴BE=BC﹣EC=4﹣EG,EF=EG+FG=EG+1,BF=AB﹣AF=4﹣1=3,
在Rt△BEF中,根据勾股定理,得BE2+BF2=EF2,
∴(4﹣EG)2+32=(EG+1)2,
解得EG=2.4,
∴EF=EG+FG=2.4+1=3.4,
∴EF的长为3.4.
故答案为:3.4.
三、解答题
17.【解答】解:(1)如图,△A1B1C1即为所求;
;
(2)如图,△D1EF1即为所求;
(3)根据旋转的性质可得,旋转中心为AD和CF垂直平分线的交点,图中点P即为旋转中心,
∴P(0,1),
故答案为:(0,1).
18.【解答】解:(1)样本中最喜欢A项目的人数所占的百分比为1﹣30%﹣10%﹣20%=40%,
其所在扇形统计图中对应的圆心角度数是360°×40%=144,
故答案为:40%,144;
(2)本次抽查的学生人数是:15÷30%=50(人),
∴喜欢A:篮球的人数是:50﹣15﹣5﹣10=20(人),
作图如下:
(3)3000×20%=600人,
答:根据样本估计全校最喜欢足球的学生人数约是600人.
19.【解答】解:(1)通过以上实验,摸到红球的概率估计为0.3,
盒子里红球的数量为:20×0.3=6(个).
故答案为:6;
(2)∵盒子里有6个红球,“摸出黑球”为必然事件,
∴x=6.
故答案为:6;
(3)由(1)知红球6个,黑球14个,根据题意得:
,
解得:x=1,
则x的值为1.
20.【解答】(1)证明:∵AD⊥CD及DE=AD
∴∠E=45°,
∵AB∥CD,
∴∠EAB+∠E=180°,
∴∠EAB=180°﹣∠E=135°,
∵∠B=45°,
∴∠EAB+∠B=180°,
∴AE∥BC,
∴四边形ABCE平行四边形,
∴AE=BC;
(2)解:∵四边形ABCE平行四边形,
∴CE=AB=6,
∴AD=DE=CE﹣CD=4,
∴四边形ABCE的面积为:AB AD=6×4=24.
21.【解答】(1)证明:
∵CE∥BD,DE∥AC,
∴四边形CODE为平行四边形,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠COD=90°,
∴平行四边形CODE是矩形;
(2)解:
∵四边形ABCD为菱形,
∴AO=OCAC6=3,OD=OB,∠AOB=90°,
在Rt△AOB中,由勾股定理得BO2=AB2﹣AO2,
∴BO4,
∴DO=BO=4,
∴四边形CODE的周长=2×(3+4)=14.
22.【解答】(1)证明:∵将矩形纸片折叠,使点B与点D重合,点A落在点E处,FG是折痕,
∴BF=DF,BG=DG,∠BFG=∠DFG,
∵四边形ABCD是矩形,
∴AD=BC=8,AD∥BC,
∴∠DFG=∠BGF,
∴∠BFG=∠BGF,
∴BF=BG,
∴BF=DF=BG=DG,
∴四边形BGDF是菱形;
(2)解:过F作FM⊥BC于M,则∠FMC=∠FMB=90°,
∵四边形ABCD是矩形,
∴∠A=∠ABM=90°,
∴四边形ABMF是矩形,
∴AB=FM=6,AF=BM,
设AF=x,则BF=DF=8﹣x,
在Rt△BAF中,由勾股定理得:AB2+AF2=BF2,
即62+x2=(8﹣x)2,
解得:x,
即AF,BG=8﹣x,
∴MG=BG﹣BM,
在Rt△FMG中,由勾股定理得:FG.
23.【解答】解:(1)在长方形ABCD中,AD∥BC
∴∠DEF=∠EFB.
∵∠DEF=∠BEF,
∴∠EFB=∠BEF,
∴BE=BF;
(2)设DE=xcm,则BE=xcm,AE=(8﹣x)cm,
在Rt△ABE中,由勾股定理42+(8﹣x) 2=x2,
∴x=5,即DE的长为5cm.
(3)过E作EH⊥BF于点H,
∵EH=AB=4,BH=AE=3
∴HF=BF﹣BH=5﹣3=2,
∴EF2=22+42=20,
∴以EF为边长的正方形的面积为20cm2.
24.【解答】解:(1)①∵C(4,2),∠AOD=90°,
∴DC=AD=4,DO=2,
∴OA2,
∵四边形ABCD为菱形,
∴AB=AD=4.
∴OB=AB﹣OA=2.
∴B(2,0).
故答案为:(2,0).
②∵在菱形ABCD中,DC=AB=4,OD=2,
∴菱形ABCD的面积=AB OD=4×28.
(2)如图1所示:
在菱形ABCD中,点P关于AC的对称点为P',AP'=3,
连接DP'交AC于点E,连接PE,
∴PE+DE=P'E+ED=P'D.
∵OA=2,OD=2,
∴OP'=1,
在Rt△DOP'中,
∵DO2+P'O2=P'D2,
∴.
∴PE+DE的最小值为.
(3)如图2所示:①当点P在AD上时,过点P作PE⊥AC,垂足为E.
由菱形的性质可知:∠PAE∠DAB=30°,
∵PE=1,∠PAE=30°,∠PEA=90°,
∴AP=2.
∴t=2.
②当点P在DC上时,如图3所示:
由菱形的性质可知:∠PCE∠DCB=30°,
∵PE=1,∠PCE=30°,∠PEC=90°,
∴CP=2.
∴AD+DP=4+2=6.
∴t=6.
③如图4所示:当点P在BC上时.
由菱形的性质可知:∠PCE∠DCB=30°,
∵PE=1,∠PCE=30°,∠PEC=90°,
∴CP=2.
∴AD+DC+CP=4+4+2=10.
∴t=10.
④如图5所示;点P在AB上时.
由菱形的性质可知:∠PAE∠DAB=30°,
∵PE=1,∠PAE=30°,∠PEA=90°,
∴AP=2.
∴AD+DC+BC+BP=4+4+4+2=14.
∴t=14.
综上所述,当t=2或t=6或t=10或t=14时,点P到AC的距离是1.
故答案为:2,6,10,14.
25.【解答】解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ADB=∠CBD,
由折叠可得:∠ADB=∠A′DB,
∴∠CBD=∠A′DB,
∴DE=BE.
(2)∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∵A(0,0),B(4,0),D(0,8),
∴C(4,8),
∴CD=4,BC=8,
由(1)知,DE=BE,
∴CE=BC﹣BE=BC﹣DE=8﹣DE,
在Rt△CDE中,DE2﹣CE2=CD2,
∴DE2﹣(8﹣DE)2=16,解得:DE=5,
∴BE=DE=5,
∵点E在BC上,
∴E(4,5),
设直线DE的解析式为y=kx+8,
∴4k+8=5,
∴,
∴直线DE的解析式为.
(3)∵以M,N,E,F为顶点的四边形是平行四边形,
∴①当EF为对角线时,MN于EF互相平分,
∴MN的中点也是EF的中点,
由(2)知,E(4,5),
∵F(0,1),
∴EF的中点坐标为E(2,3),
设,N(n,0),
∴m+n=4,,
∴,,
∴,;
②当EF为边时,
a.EM,FN为对角线时,EF∥MN,EM∥FN,
由(2)知,直线DE的解析式为,
∵点F(0,1)
∴直线FN的解析式为,
∴,
∵E(4,5),F(0,1),
根据待定系数法可得:直线EF的解析式为y=x+1,
∵EF∥MN,
∴直线MN的解析式为y=x,
联立,解得:,
∴M(,4);
②FN,EM为对角线时,FN的中点,也是EM的中点,
∴FN的中点在直线DE上,
设N(a,0),
∵F(0,1),
∴FN的中点坐标为,
∵直线DE的解析式为,
∴,
∴a=20,
∴FN的中点坐标为,
设,
∵E(4,5),
∴b+4=2×10,解得:b=16,
∴M(16,﹣4),
∴满足条件的点,(,4),(16,﹣4).
21世纪教育网(www.21cnjy.com)
同课章节目录
