苏科版2024—2025学年七年级下册数学期中考试模拟试卷(含解析)
文档属性
| 名称 | 苏科版2024—2025学年七年级下册数学期中考试模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 347.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-18 17:15:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏科版2024—2025学年七年级下册数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列运算正确的是( )
A.2a2+a2=3a4 B.a6÷a2=a3
C.4a3 a2=4a5 D.(﹣3a3)3=﹣9a9
2.已知(xm yn y)3=x9y15,则m、n的值分别为( )
A.3、4 B.4、3 C.3、5 D.9、6
3.下列图案中,可以看成由某一个基本图形通过平移形成的是( )
A. B. C. D.
4.已知3m=4,3n=6,则32m﹣n=( )
A.2 B.10 C. D.
5.下列图形中,不是轴对称图形的是( )
A. B. C. D.
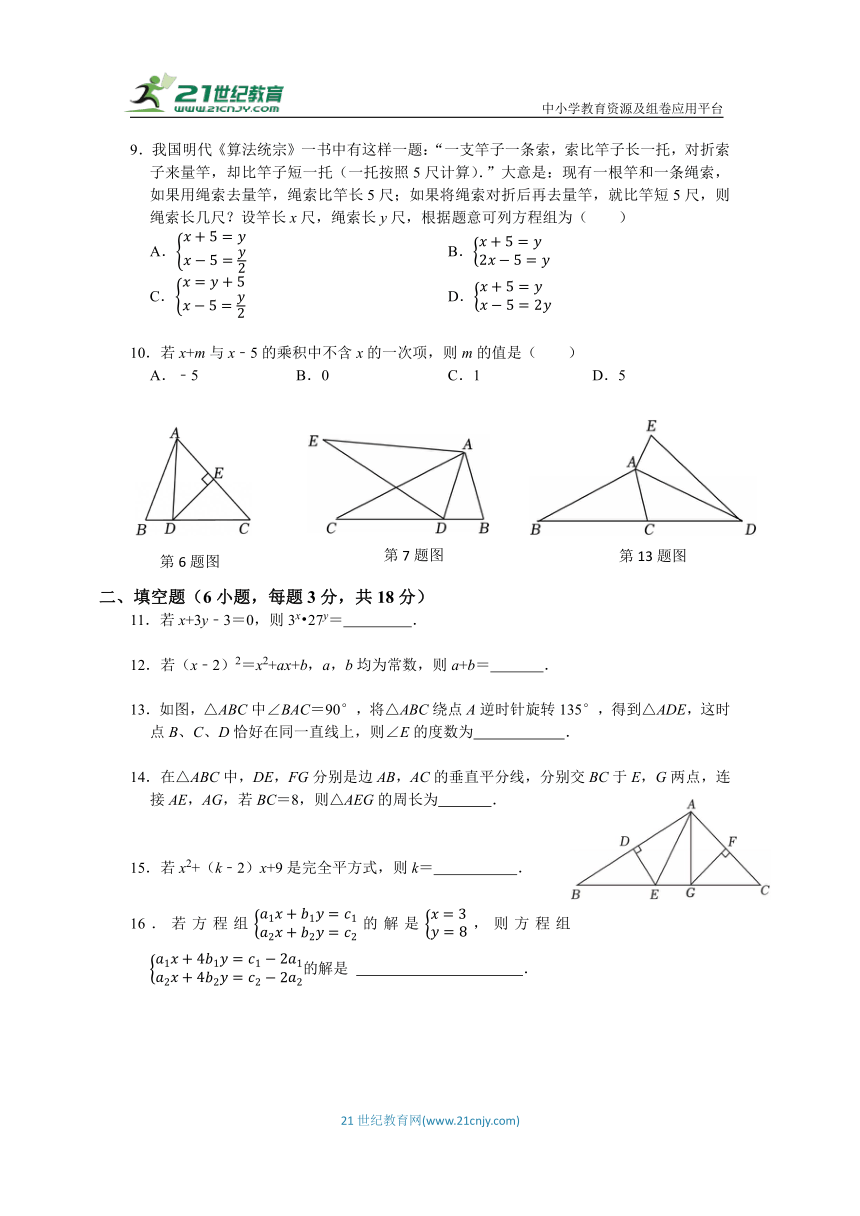
6.如图,在△ABC中,AB=8,BC=12,AC的垂直平分线交BC于点D,垂足为E,则△ABD的周长为( )
A.14 B.20 C.28 D.32
7.如图,将△ABC绕点A顺时针旋转40°得到△ADE,点B的对应点D恰好落在边BC上,则∠ADE的度数为( )
A.40° B.70° C.80° D.75°
8.若关于x,y的二元一次方程组的解也是二元一次方程2x﹣y=﹣7的解,则k的值是( )
A.﹣1 B.0 C.1 D.2
9.我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )
A. B.
C. D.
10.若x+m与x﹣5的乘积中不含x的一次项,则m的值是( )
A.﹣5 B.0 C.1 D.5
二、填空题(6小题,每题3分,共18分)
11.若x+3y﹣3=0,则3x 27y= .
12.若(x﹣2)2=x2+ax+b,a,b均为常数,则a+b= .
13.如图,△ABC中∠BAC=90°,将△ABC绕点A逆时针旋转135°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为 .
14.在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 .
15.若x2+(k﹣2)x+9是完全平方式,则k= .
16.若方程组的解是,则方程组的解是 .
第II卷
苏科版2024—2025学年七年级下册数学期中考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:(a﹣b)2﹣2a(a﹣3b)+(a﹣b)(b﹣a),其中a=﹣1,b=1.
18.解方程组:
(1); (2).
19.计算题.
(1).
(2)28x8y4÷(﹣7x4y4)+(3x2)2.
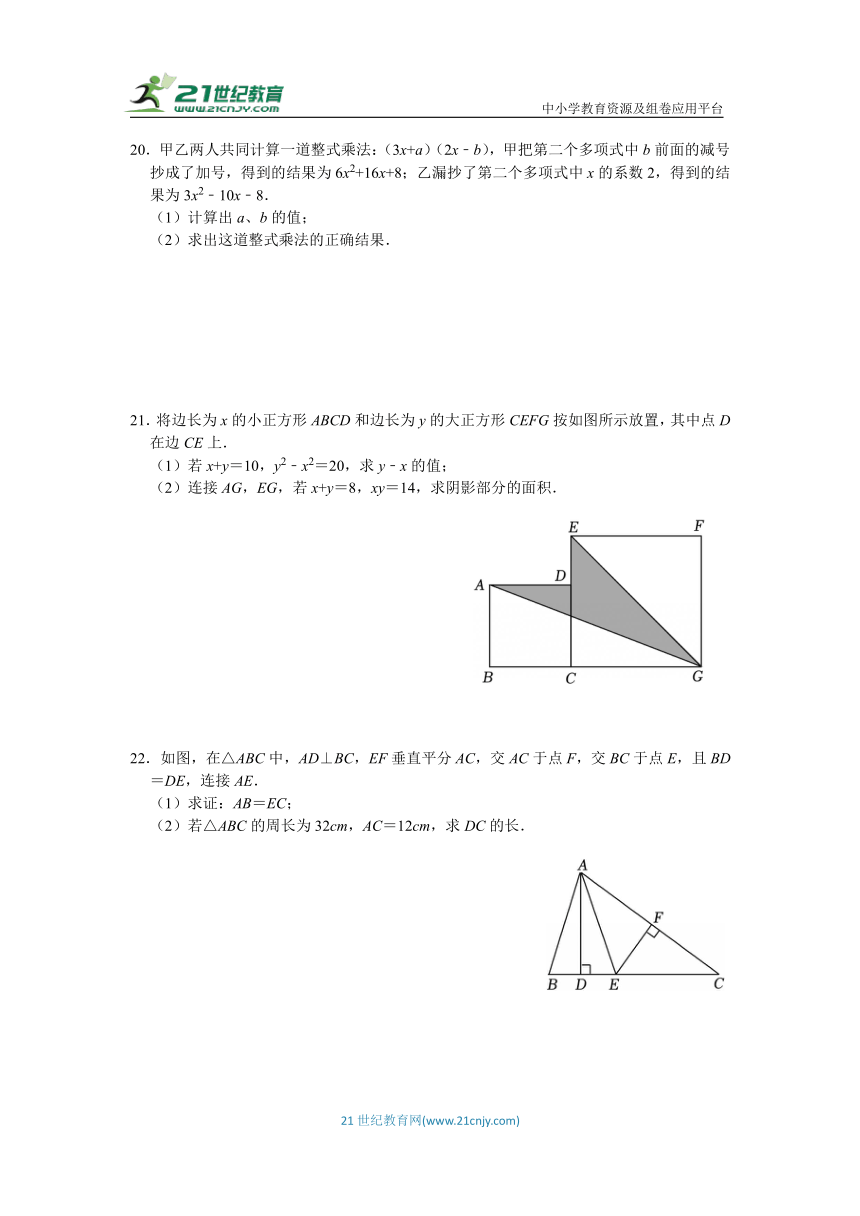
20.甲乙两人共同计算一道整式乘法:(3x+a)(2x﹣b),甲把第二个多项式中b前面的减号抄成了加号,得到的结果为6x2+16x+8;乙漏抄了第二个多项式中x的系数2,得到的结果为3x2﹣10x﹣8.
(1)计算出a、b的值;
(2)求出这道整式乘法的正确结果.
21.将边长为x的小正方形ABCD和边长为y的大正方形CEFG按如图所示放置,其中点D在边CE上.
(1)若x+y=10,y2﹣x2=20,求y﹣x的值;
(2)连接AG,EG,若x+y=8,xy=14,求阴影部分的面积.
22.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为32cm,AC=12cm,求DC的长.
23.某书店购进甲、乙两种图书共100本,甲、乙两种图书的进价分别为每本10元、30元,甲、乙两种图书的标价分别定为每本15元、40元.
(1)若书店恰好用了2300元购进这100本图书,求购进的甲、乙图书各多少本?
(2)在(1)的结论下,在销售时,该书店考虑到要迅速将图书售完,于是甲图书打8折,乙图书也打折进行促销,为使甲、乙两种图书全部销售完后共获利460元,请问乙图书应打几折出售?
24.我们把关于x、y的两个二元一次方程ax+by=c与bx+ay=c(a≠b)叫作互为共轭二元一次方程:二元一次方程组,叫做关于x、y共轭二元一次方程组.例如:2x﹣y=3与﹣x+2y=3互为共轭二元一次方程,二元一次方程组,叫做关于x、y共轭二元一次方程组;2(x﹣1)﹣(y+2)=3与﹣(x﹣1)+2(y+2)=3互为共轭二元一次方程,二元一次方程组,叫做关于x﹣1、y+2的共轭二元一次方程组.
(1)若关于x、y的方程组,为共轭方程组,则a= ,b= ;
(2)若二元一次方程x+by=1中x、y的值满足下列表格:
x 1 0
y 0 2
则这个方程的共轭二元一次方程是 .
(3)解下列方程组(直接写出方程组的解即可):的解为 .
(4)发现:若方程组是共轭方程组,且方程组的解是,请计算n2﹣mn﹣n+2025的值.
25.我们定义:如果两个多项式M与N的和为常数,则称M与N互为“对消多项式”,这个常数称为它们的“对消值”.如MF=2x2﹣x+6与N=﹣2x2+x﹣1互为“对消多项式”,它们的“对消值”为5.
(1)下列各组多项式互为“对消多项式”的是 (填序号):
①3x2+2x与3x2+2;
②x﹣6与﹣x+2;
③﹣5x2y3+2xy与5x2y3﹣2xy﹣1.
(2)多项式A=(x﹣a)2与多项式B=﹣bx2﹣2x+b(a,b为常数)互为“对消多项式”,求它们的“对消值”;
(3)关于x的多项式C=mx2+6x+4与D=﹣m(x+1)(x+n)互为“对消多项式”,“对消值”为t.若a﹣b=m,b﹣c=mn,求代数式a2+b2+c2﹣ab﹣bc﹣ac+2t的最小值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C D B B B A A D
1.【解答】解:A、2a2+a2=3a2,原式计算错误,不符合题意;
B、a6÷a2=a4,原式计算错误,不符合题意;
C、4a3 a2=4a5,原式计算正确,符合题意;
D、(﹣3a3)3=﹣27a9,原式计算错误,不符合题意.
故选:C.
2.【解答】解:根据(xm yn y)3=x9y15得x3m y3n+3=x9y15,
故3m=9,3n+3=15,
解得m=3,n=4,
故选:A.
3.【解答】解:A、不能看成由某一个基本图形通过平移形成的,故不符合题意;
B、不能看成由某一个基本图形通过平移形成的,故不符合题意;
C、能看成由某一个基本图形通过平移形成的,故符合题意;
D、不能看成由某一个基本图形通过平移形成的,故不符合题意.
故选:C.
4.【解答】解:∵3m=4,3n=6,
∴.
故选:D.
5.【解答】解:由题意可知,只有选项B的图形不能找到一条直线,使图形沿直线对折后两边完全重合,故选项B不是轴对称图形.
故选:B.
6.【解答】解:∵AC的垂直平分线交BC于点D,交AC于点E,
∴AD=DC,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=8+12=20,
故选:B.
7.【解答】解:∵将△ABC绕点A顺时针旋转40°得到△ADE,
∴∠DAB=40°,
∵AD=AB,
∴∠B=∠ADB=(180°﹣40°)÷2=70°,
∴∠ADE=70°,
故选:B.
8.【解答】解:,
①+②得:2x=6k,
解得:x=3k,
②﹣①得:2y=﹣2k,
解得:y=﹣k,
代入2x﹣y=﹣7得:6k+k=﹣7,
解得:k=﹣1
故选:A.
9.【解答】解:根据第一次用绳索去量竿,绳索比竿长5尺,可得出方程为x+5=y;又根据第二次将绳索对折去量竿,就比竿短5尺,可得出方程为x﹣5,那么方程组是.
故选:A.
10.【解答】解:(x+m)(x﹣5)=x2+(m﹣5)x﹣5m,
∵x+m与x﹣5的乘积中不含x的一次项,
∴m﹣5=0,
解得:m=5,
故选:D.
二、填空题
11.【解答】解:∵x+3y﹣3=0,
∴x+3y=3,
∴3x 27y=3x+3y=33=27,
故答案为:27.
12.【解答】解:∵(x﹣2)2=x2+ax+b,
∴(x﹣2)2=x2﹣4x+4=x2+ax+b,
∴a=﹣4,b=4,
∴a+b=﹣4+4=0.
所以答案为:0.
13.【解答】解:∵将△ABC绕点A逆时针旋转135°,得到△ADE,
∴AB=AD,∠BAD=135°,∠E=∠ACB,
∴,
∵∠BAC=90°,
∴∠E=∠ACB=90°﹣∠B=90°﹣22.5°=67.5°,
故答案为:67.5°.
14.【解答】解:∵DE,FG分别是边AB,AC的垂直平分线,
∴AE=BE,AG=CG,
∴BC=BE+EG+CG=AE+EG+AG,
∴△AEG的周长=AE+EG+AG=BC=8.
故答案为:8.
15.【解答】解:由题意得:x2+(k﹣2)x+9=(x±3)2,
∴x2+(k﹣2)x+9=x2±6x+9,
∴k﹣2=±6,
解得:k=8或﹣4,
故答案为:8或﹣4.
16.【解答】解:∵,
∴,
∵方程组的解是,
∴,
∴,
∴方程组的解是.
故答案为:.
三、解答题
17.【解答】解:(a﹣b)2﹣2a(a﹣3b)+(a﹣b)(b﹣a)
=a2﹣2ab+b2﹣2a2+6ab﹣a2+2ab﹣b2
=﹣2a2+6ab,
∵a=﹣1,b=1,
∴原式=﹣2a2+6ab=﹣2×(﹣1)2+6×(﹣1)×1=﹣8.
18.【解答】解:(1),
①+②得:5x=10,
解得:x=2,
将x=2代入①得:3×2+y=9,
解得:y=3,
∴方程组的解为:;
(2),
将②代入①得:3(3﹣2y)﹣4y=4,
解得:,
将代入②得:,
解得:x=2,
∴方程组的解为:.
19.【解答】解:(1)原式=1+9+1
=11;
(2)原式=28x8y4÷(﹣7x4y4)+9x4
=﹣4x4+9x4
=5x4.
20.【解答】解:(1)甲的算式:(3x+a)(2x+b)=6x2+(3b+2a)x+ab=6x2+16x+8,
对应的系数相等,3b+2a=16,ab=8,
乙的算式:(3x+a)(x﹣b)=3x2+(﹣3b+a)x﹣ab=3x2﹣10x﹣8,
对应的系数相等,﹣3b+a=﹣10,ab=8,
∴,
解得:;
(2)根据(1)可得正确的式子:(3x+2)(2x﹣4)=6x2﹣8x﹣8.
21.【解答】解:(1)∵y2﹣x2=20,即(y+x)(y﹣x)=20,而x+y=10,
∴y﹣x=2,
答:y﹣x的值为2;
(2)由题意得,
S阴影部分=S正方形ABCD+S正方形CEFG﹣S△ABG﹣S△EFG
=x2+y2x(x+y)y2
x2xyy2
[(x+y)2﹣2xy]xy
当x+y=8,xy=14时,
原式(64﹣28)14
=18﹣7
=11,
答:阴影部分的面积是11.
22.【解答】(1)证明:∵EF垂直平分AC,
根据线段的垂直平分线的性质可得:AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC.
(2)解:由题意可得:AB+BC+AC=32cm,
∵AC=12cm,
∴AB+BC=20cm,
∵AB=EC,BD=DE,
∴DC=DE+EC
=10cm.
23.【解答】解:(1)设购进甲图书x本,乙图书y本,
依题意,得:,
解得:.
答:购进甲图书35本,乙图书65本.
(2)设乙图书应打a折出售,
由题意可得,(15×0.8﹣10)×35+(4030)×65=460,
解得a=9;
答:乙图书应打9折出售.
24.【解答】解:(1)由定义可得:1﹣a=2,b+2=3,
∴a=﹣1,b=1.
故答案为:﹣1,1.
(2)将x=0,y=2代入x+by=1,得2b=1,
解得b,
∴二元一次方程为x,
∴共轭二元一次方程为:,
故答案为:;
(3),
①+②得:﹣x﹣y=2,即x+y=﹣2③,
①+③得:4049x=﹣4049,
解得x=﹣1,
将x=﹣1代入③得y=﹣1,
∴方程组的解为:;
故答案为:;
(4)∵方程组是共轭方程组,
∴a≠b,(a﹣b)x﹣(a﹣b)y=﹣(a﹣b).
∴x﹣y=﹣1.
又∵方程组的解是,
∴m﹣n=﹣1.
∴n2﹣mn﹣n+2025
=n(n﹣m)﹣n+2025
=n×1﹣n+2025
=2025.
25.【解答】解:(1)∵3x2+2x+3x2+2=6x2+2x+2,
x﹣6﹣x+2=﹣4,
﹣5x2y3+2xy+5x2y3﹣2xy﹣1=﹣1,
∴①组多项式不是互为“对消多项式”,
②③组多项式是互为“对消多项式”,
故答案为:②③;
(2)∵A=(x﹣a)2=x2﹣2ax+a2,B=﹣bx2﹣2x+b,
∴A+B
=x2﹣2ax+a2﹣bx2﹣2x+b
=(1﹣b)x2+(﹣2a﹣2)x+(a2+b),
∵A与B互为“对消多项式”,
∴1﹣b=0,﹣2a﹣2=0,
解得a=﹣1,b=1.
∴a2+b
=(﹣1)2+1
=1+1
=2,
∴它们的“对消值”是2;
(3)∵C=mx2+6x+4,D=﹣m(x+1)(x+n)=﹣mx2+(﹣mn﹣m)x﹣mn,
∴C+D=(6﹣mn﹣m)x+(4﹣mn),
∵C与D互为“对消多项式”且“对消值”为t,
∵a﹣b=m,b﹣c=mn,
∴a﹣c=(a﹣b)+(b﹣c)=m+mn=6,
∴a2+b2+c2﹣ab﹣bc﹣ac+2t
=m2﹣4m+32
=(m﹣2)2+28≥28,
∴代数式 a2+b2+c2=ab=bc=ac+2 的最小值是28.
21世纪教育网(www.21cnjy.com)
苏科版2024—2025学年七年级下册数学期中考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列运算正确的是( )
A.2a2+a2=3a4 B.a6÷a2=a3
C.4a3 a2=4a5 D.(﹣3a3)3=﹣9a9
2.已知(xm yn y)3=x9y15,则m、n的值分别为( )
A.3、4 B.4、3 C.3、5 D.9、6
3.下列图案中,可以看成由某一个基本图形通过平移形成的是( )
A. B. C. D.
4.已知3m=4,3n=6,则32m﹣n=( )
A.2 B.10 C. D.
5.下列图形中,不是轴对称图形的是( )
A. B. C. D.
6.如图,在△ABC中,AB=8,BC=12,AC的垂直平分线交BC于点D,垂足为E,则△ABD的周长为( )
A.14 B.20 C.28 D.32
7.如图,将△ABC绕点A顺时针旋转40°得到△ADE,点B的对应点D恰好落在边BC上,则∠ADE的度数为( )
A.40° B.70° C.80° D.75°
8.若关于x,y的二元一次方程组的解也是二元一次方程2x﹣y=﹣7的解,则k的值是( )
A.﹣1 B.0 C.1 D.2
9.我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )
A. B.
C. D.
10.若x+m与x﹣5的乘积中不含x的一次项,则m的值是( )
A.﹣5 B.0 C.1 D.5
二、填空题(6小题,每题3分,共18分)
11.若x+3y﹣3=0,则3x 27y= .
12.若(x﹣2)2=x2+ax+b,a,b均为常数,则a+b= .
13.如图,△ABC中∠BAC=90°,将△ABC绕点A逆时针旋转135°,得到△ADE,这时点B、C、D恰好在同一直线上,则∠E的度数为 .
14.在△ABC中,DE,FG分别是边AB,AC的垂直平分线,分别交BC于E,G两点,连接AE,AG,若BC=8,则△AEG的周长为 .
15.若x2+(k﹣2)x+9是完全平方式,则k= .
16.若方程组的解是,则方程组的解是 .
第II卷
苏科版2024—2025学年七年级下册数学期中考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:(a﹣b)2﹣2a(a﹣3b)+(a﹣b)(b﹣a),其中a=﹣1,b=1.
18.解方程组:
(1); (2).
19.计算题.
(1).
(2)28x8y4÷(﹣7x4y4)+(3x2)2.
20.甲乙两人共同计算一道整式乘法:(3x+a)(2x﹣b),甲把第二个多项式中b前面的减号抄成了加号,得到的结果为6x2+16x+8;乙漏抄了第二个多项式中x的系数2,得到的结果为3x2﹣10x﹣8.
(1)计算出a、b的值;
(2)求出这道整式乘法的正确结果.
21.将边长为x的小正方形ABCD和边长为y的大正方形CEFG按如图所示放置,其中点D在边CE上.
(1)若x+y=10,y2﹣x2=20,求y﹣x的值;
(2)连接AG,EG,若x+y=8,xy=14,求阴影部分的面积.
22.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为32cm,AC=12cm,求DC的长.
23.某书店购进甲、乙两种图书共100本,甲、乙两种图书的进价分别为每本10元、30元,甲、乙两种图书的标价分别定为每本15元、40元.
(1)若书店恰好用了2300元购进这100本图书,求购进的甲、乙图书各多少本?
(2)在(1)的结论下,在销售时,该书店考虑到要迅速将图书售完,于是甲图书打8折,乙图书也打折进行促销,为使甲、乙两种图书全部销售完后共获利460元,请问乙图书应打几折出售?
24.我们把关于x、y的两个二元一次方程ax+by=c与bx+ay=c(a≠b)叫作互为共轭二元一次方程:二元一次方程组,叫做关于x、y共轭二元一次方程组.例如:2x﹣y=3与﹣x+2y=3互为共轭二元一次方程,二元一次方程组,叫做关于x、y共轭二元一次方程组;2(x﹣1)﹣(y+2)=3与﹣(x﹣1)+2(y+2)=3互为共轭二元一次方程,二元一次方程组,叫做关于x﹣1、y+2的共轭二元一次方程组.
(1)若关于x、y的方程组,为共轭方程组,则a= ,b= ;
(2)若二元一次方程x+by=1中x、y的值满足下列表格:
x 1 0
y 0 2
则这个方程的共轭二元一次方程是 .
(3)解下列方程组(直接写出方程组的解即可):的解为 .
(4)发现:若方程组是共轭方程组,且方程组的解是,请计算n2﹣mn﹣n+2025的值.
25.我们定义:如果两个多项式M与N的和为常数,则称M与N互为“对消多项式”,这个常数称为它们的“对消值”.如MF=2x2﹣x+6与N=﹣2x2+x﹣1互为“对消多项式”,它们的“对消值”为5.
(1)下列各组多项式互为“对消多项式”的是 (填序号):
①3x2+2x与3x2+2;
②x﹣6与﹣x+2;
③﹣5x2y3+2xy与5x2y3﹣2xy﹣1.
(2)多项式A=(x﹣a)2与多项式B=﹣bx2﹣2x+b(a,b为常数)互为“对消多项式”,求它们的“对消值”;
(3)关于x的多项式C=mx2+6x+4与D=﹣m(x+1)(x+n)互为“对消多项式”,“对消值”为t.若a﹣b=m,b﹣c=mn,求代数式a2+b2+c2﹣ab﹣bc﹣ac+2t的最小值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C D B B B A A D
1.【解答】解:A、2a2+a2=3a2,原式计算错误,不符合题意;
B、a6÷a2=a4,原式计算错误,不符合题意;
C、4a3 a2=4a5,原式计算正确,符合题意;
D、(﹣3a3)3=﹣27a9,原式计算错误,不符合题意.
故选:C.
2.【解答】解:根据(xm yn y)3=x9y15得x3m y3n+3=x9y15,
故3m=9,3n+3=15,
解得m=3,n=4,
故选:A.
3.【解答】解:A、不能看成由某一个基本图形通过平移形成的,故不符合题意;
B、不能看成由某一个基本图形通过平移形成的,故不符合题意;
C、能看成由某一个基本图形通过平移形成的,故符合题意;
D、不能看成由某一个基本图形通过平移形成的,故不符合题意.
故选:C.
4.【解答】解:∵3m=4,3n=6,
∴.
故选:D.
5.【解答】解:由题意可知,只有选项B的图形不能找到一条直线,使图形沿直线对折后两边完全重合,故选项B不是轴对称图形.
故选:B.
6.【解答】解:∵AC的垂直平分线交BC于点D,交AC于点E,
∴AD=DC,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=8+12=20,
故选:B.
7.【解答】解:∵将△ABC绕点A顺时针旋转40°得到△ADE,
∴∠DAB=40°,
∵AD=AB,
∴∠B=∠ADB=(180°﹣40°)÷2=70°,
∴∠ADE=70°,
故选:B.
8.【解答】解:,
①+②得:2x=6k,
解得:x=3k,
②﹣①得:2y=﹣2k,
解得:y=﹣k,
代入2x﹣y=﹣7得:6k+k=﹣7,
解得:k=﹣1
故选:A.
9.【解答】解:根据第一次用绳索去量竿,绳索比竿长5尺,可得出方程为x+5=y;又根据第二次将绳索对折去量竿,就比竿短5尺,可得出方程为x﹣5,那么方程组是.
故选:A.
10.【解答】解:(x+m)(x﹣5)=x2+(m﹣5)x﹣5m,
∵x+m与x﹣5的乘积中不含x的一次项,
∴m﹣5=0,
解得:m=5,
故选:D.
二、填空题
11.【解答】解:∵x+3y﹣3=0,
∴x+3y=3,
∴3x 27y=3x+3y=33=27,
故答案为:27.
12.【解答】解:∵(x﹣2)2=x2+ax+b,
∴(x﹣2)2=x2﹣4x+4=x2+ax+b,
∴a=﹣4,b=4,
∴a+b=﹣4+4=0.
所以答案为:0.
13.【解答】解:∵将△ABC绕点A逆时针旋转135°,得到△ADE,
∴AB=AD,∠BAD=135°,∠E=∠ACB,
∴,
∵∠BAC=90°,
∴∠E=∠ACB=90°﹣∠B=90°﹣22.5°=67.5°,
故答案为:67.5°.
14.【解答】解:∵DE,FG分别是边AB,AC的垂直平分线,
∴AE=BE,AG=CG,
∴BC=BE+EG+CG=AE+EG+AG,
∴△AEG的周长=AE+EG+AG=BC=8.
故答案为:8.
15.【解答】解:由题意得:x2+(k﹣2)x+9=(x±3)2,
∴x2+(k﹣2)x+9=x2±6x+9,
∴k﹣2=±6,
解得:k=8或﹣4,
故答案为:8或﹣4.
16.【解答】解:∵,
∴,
∵方程组的解是,
∴,
∴,
∴方程组的解是.
故答案为:.
三、解答题
17.【解答】解:(a﹣b)2﹣2a(a﹣3b)+(a﹣b)(b﹣a)
=a2﹣2ab+b2﹣2a2+6ab﹣a2+2ab﹣b2
=﹣2a2+6ab,
∵a=﹣1,b=1,
∴原式=﹣2a2+6ab=﹣2×(﹣1)2+6×(﹣1)×1=﹣8.
18.【解答】解:(1),
①+②得:5x=10,
解得:x=2,
将x=2代入①得:3×2+y=9,
解得:y=3,
∴方程组的解为:;
(2),
将②代入①得:3(3﹣2y)﹣4y=4,
解得:,
将代入②得:,
解得:x=2,
∴方程组的解为:.
19.【解答】解:(1)原式=1+9+1
=11;
(2)原式=28x8y4÷(﹣7x4y4)+9x4
=﹣4x4+9x4
=5x4.
20.【解答】解:(1)甲的算式:(3x+a)(2x+b)=6x2+(3b+2a)x+ab=6x2+16x+8,
对应的系数相等,3b+2a=16,ab=8,
乙的算式:(3x+a)(x﹣b)=3x2+(﹣3b+a)x﹣ab=3x2﹣10x﹣8,
对应的系数相等,﹣3b+a=﹣10,ab=8,
∴,
解得:;
(2)根据(1)可得正确的式子:(3x+2)(2x﹣4)=6x2﹣8x﹣8.
21.【解答】解:(1)∵y2﹣x2=20,即(y+x)(y﹣x)=20,而x+y=10,
∴y﹣x=2,
答:y﹣x的值为2;
(2)由题意得,
S阴影部分=S正方形ABCD+S正方形CEFG﹣S△ABG﹣S△EFG
=x2+y2x(x+y)y2
x2xyy2
[(x+y)2﹣2xy]xy
当x+y=8,xy=14时,
原式(64﹣28)14
=18﹣7
=11,
答:阴影部分的面积是11.
22.【解答】(1)证明:∵EF垂直平分AC,
根据线段的垂直平分线的性质可得:AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC.
(2)解:由题意可得:AB+BC+AC=32cm,
∵AC=12cm,
∴AB+BC=20cm,
∵AB=EC,BD=DE,
∴DC=DE+EC
=10cm.
23.【解答】解:(1)设购进甲图书x本,乙图书y本,
依题意,得:,
解得:.
答:购进甲图书35本,乙图书65本.
(2)设乙图书应打a折出售,
由题意可得,(15×0.8﹣10)×35+(4030)×65=460,
解得a=9;
答:乙图书应打9折出售.
24.【解答】解:(1)由定义可得:1﹣a=2,b+2=3,
∴a=﹣1,b=1.
故答案为:﹣1,1.
(2)将x=0,y=2代入x+by=1,得2b=1,
解得b,
∴二元一次方程为x,
∴共轭二元一次方程为:,
故答案为:;
(3),
①+②得:﹣x﹣y=2,即x+y=﹣2③,
①+③得:4049x=﹣4049,
解得x=﹣1,
将x=﹣1代入③得y=﹣1,
∴方程组的解为:;
故答案为:;
(4)∵方程组是共轭方程组,
∴a≠b,(a﹣b)x﹣(a﹣b)y=﹣(a﹣b).
∴x﹣y=﹣1.
又∵方程组的解是,
∴m﹣n=﹣1.
∴n2﹣mn﹣n+2025
=n(n﹣m)﹣n+2025
=n×1﹣n+2025
=2025.
25.【解答】解:(1)∵3x2+2x+3x2+2=6x2+2x+2,
x﹣6﹣x+2=﹣4,
﹣5x2y3+2xy+5x2y3﹣2xy﹣1=﹣1,
∴①组多项式不是互为“对消多项式”,
②③组多项式是互为“对消多项式”,
故答案为:②③;
(2)∵A=(x﹣a)2=x2﹣2ax+a2,B=﹣bx2﹣2x+b,
∴A+B
=x2﹣2ax+a2﹣bx2﹣2x+b
=(1﹣b)x2+(﹣2a﹣2)x+(a2+b),
∵A与B互为“对消多项式”,
∴1﹣b=0,﹣2a﹣2=0,
解得a=﹣1,b=1.
∴a2+b
=(﹣1)2+1
=1+1
=2,
∴它们的“对消值”是2;
(3)∵C=mx2+6x+4,D=﹣m(x+1)(x+n)=﹣mx2+(﹣mn﹣m)x﹣mn,
∴C+D=(6﹣mn﹣m)x+(4﹣mn),
∵C与D互为“对消多项式”且“对消值”为t,
∵a﹣b=m,b﹣c=mn,
∴a﹣c=(a﹣b)+(b﹣c)=m+mn=6,
∴a2+b2+c2﹣ab﹣bc﹣ac+2t
=m2﹣4m+32
=(m﹣2)2+28≥28,
∴代数式 a2+b2+c2=ab=bc=ac+2 的最小值是28.
21世纪教育网(www.21cnjy.com)
同课章节目录
