2.1 第1课时 两条直线的位置关系 课件(33张PPT)
文档属性
| 名称 | 2.1 第1课时 两条直线的位置关系 课件(33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 13:57:04 | ||
图片预览










文档简介
(共33张PPT)
2024-2025学年北师版数学
七年级(上册)
1.理解对顶角、补角、余角的概念。(重点)
2.掌握对顶角、补角、余角的性质,并能运用它们的性质进行角的运算及一些实际问题。(难点)
学习·目标
情境·导入
观察下面几幅图片,你认为两条直线有哪些位置关系?
情境·导入
情境·导入
相交线
平行线
探索·交流
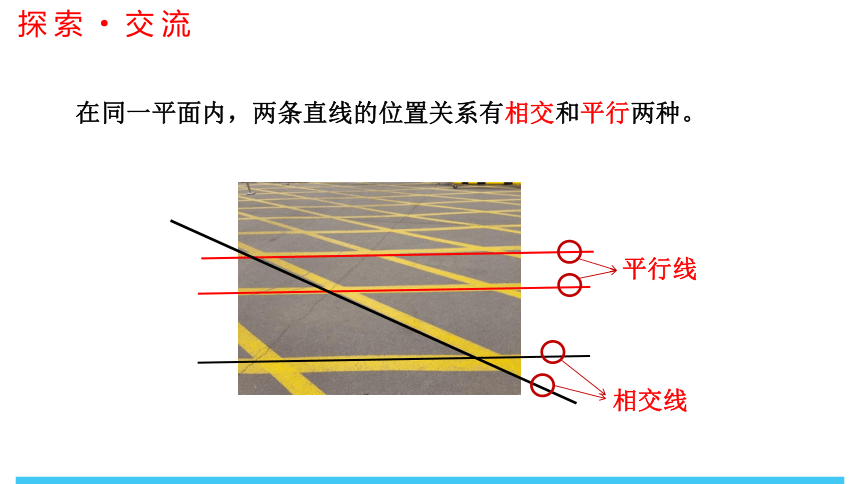
在同一平面内,两条直线的位置关系有相交和平行两种。
若两条直线只有一个公共点,我们称这两条直线为相交线。
在同一平面内,不相交的两条直线叫作平行线。
注意:平行线是指“两条直线”,而不是两条线段或射线。线段或射线平行是指它们所在的直线平行。
探索·思考
例1 下列说法正确的是( )
A.不相交的两条直线是平行线
B.在同一平面内,不相交的两条射线是平行线
C.在同一平面内,两条直线不相交就重合
D.在同一平面内,没有公共点的两条直线是平行线
D
如图,直线AB与CD相交于点O。
(1)∠1与∠2的位置有什么关系?它们的大小有什么关系?
2
1
A
B
C
D
O
3
4
观察·交流
∠1=∠2。
∠1与∠2有公共顶点O,
它们的两边互为反向延长线。
(2)你能说明理由吗?与同伴进行交流。
观察·交流
2
1
A
B
C
D
O
3
4
因为∠1+∠3=180°(平角的定义),
∠2+∠3=180°(平角的定义),
所以∠1=∠2(等量代换)。
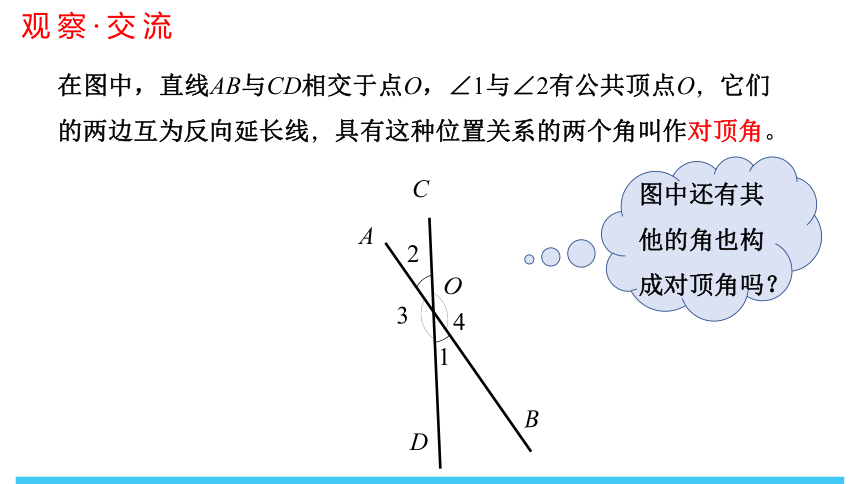
在图中,直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,具有这种位置关系的两个角叫作对顶角。
2
1
A
B
C
D
O
3
4
观察·交流
图中还有其他的角也构成对顶角吗?
对顶角有如下性质:
对顶角相等。
观察·交流
注意:对顶角是成对出现的。
2
1
A
B
C
D
O
3
4
在图中,∠1与∠3有什么数量关系?
一般地,如果两个角的和是180°,那么称这两个角互为补角。
观察·思考
2
1
A
B
C
D
O
3
4
∠1与∠3的和是180°。
图中还有其他的角也构成互为补角的关系吗?
类似地,如果两个角的和是90° ,那么称这两个角互为余角。
注意:互余与互补是指两个角之间的数量关系,与它们的位置无关。
观察·思考
例2 在数学课上,老师让同学们画对顶角(∠1与∠2),下面作图正确的是( )
D
如左图,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2。将左图简化为右图,ON与DC相交所成的∠DON和∠CON都等于90°,且∠1=∠2。
思考·交流
(1)请在图中找出互为补角和互为余角的角,并说说你的理由。
互余的角:∠1与∠3, ∠2与∠4, ∠1与∠4, ∠2与∠3。
互补的角:∠1和∠AOC,∠2和∠BOD,∠DON与∠CON,
∠1和∠DOB,∠2和∠AOC。
思考·交流
(2)∠3与∠4的大小有什么关系?∠AOC与∠BOD呢?你能说明理由吗?与同伴进行交流。
因为∠3=90°-∠1,∠4=90°-∠2,
而∠1=∠2,
所以∠3=∠4。
思考·交流
因为∠AOC=∠3+90°,∠BOD=∠4+90°,
而∠3=∠4,
所以∠AOC=∠BOD。
因为∠1=∠2,
∠1+∠AOC=180°,∠2+∠BOD=180 ,
所以 ∠AOC= ∠BOD。
补角的性质:同角(或等角)的补角相等。
几何语言:
思考·交流
因为∠1=∠2,
∠1+∠3=90°,∠2+∠4=90°,
所以 ∠3= ∠4。
余角的性质:同角(或等角)的余角相等。
几何语言:
思考·交流
∠1和∠2也是直线AB,CD相交得到的,它们不仅有一个公共顶点O,还有一条公共边OA,像这样的两个角叫作邻补角。
∠2与∠3,∠3与∠4,∠1与∠4都是邻补角。
A
B
C
D
O
1
2
3
4
邻补角的性质:邻补角互补,即互为邻补角的两个角之和为180°。
探索·交流
知识梳理
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
小结·反思
1.同一平面内两线的位置关系:
2.对顶角及其性质:
(1)对顶角的两边互为反向延长线,其实质是:对顶角是两直
线相交所成的没有公共边的两个角。
(2)性质:对顶角相等。
3.余角、补角及其性质
(1)如果两个角的和为90°,那么称这两个角互为余角;如果
两个角的和为180°,那么称这两个角互为补角。
(2)性质:同角或等角的补角相等,同角或等角的补角相等。
相交和平行。
2024-2025学年北师版数学
七年级(上册)
1.理解对顶角、补角、余角的概念。(重点)
2.掌握对顶角、补角、余角的性质,并能运用它们的性质进行角的运算及一些实际问题。(难点)
学习·目标
情境·导入
观察下面几幅图片,你认为两条直线有哪些位置关系?
情境·导入
情境·导入
相交线
平行线
探索·交流
在同一平面内,两条直线的位置关系有相交和平行两种。
若两条直线只有一个公共点,我们称这两条直线为相交线。
在同一平面内,不相交的两条直线叫作平行线。
注意:平行线是指“两条直线”,而不是两条线段或射线。线段或射线平行是指它们所在的直线平行。
探索·思考
例1 下列说法正确的是( )
A.不相交的两条直线是平行线
B.在同一平面内,不相交的两条射线是平行线
C.在同一平面内,两条直线不相交就重合
D.在同一平面内,没有公共点的两条直线是平行线
D
如图,直线AB与CD相交于点O。
(1)∠1与∠2的位置有什么关系?它们的大小有什么关系?
2
1
A
B
C
D
O
3
4
观察·交流
∠1=∠2。
∠1与∠2有公共顶点O,
它们的两边互为反向延长线。
(2)你能说明理由吗?与同伴进行交流。
观察·交流
2
1
A
B
C
D
O
3
4
因为∠1+∠3=180°(平角的定义),
∠2+∠3=180°(平角的定义),
所以∠1=∠2(等量代换)。
在图中,直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,具有这种位置关系的两个角叫作对顶角。
2
1
A
B
C
D
O
3
4
观察·交流
图中还有其他的角也构成对顶角吗?
对顶角有如下性质:
对顶角相等。
观察·交流
注意:对顶角是成对出现的。
2
1
A
B
C
D
O
3
4
在图中,∠1与∠3有什么数量关系?
一般地,如果两个角的和是180°,那么称这两个角互为补角。
观察·思考
2
1
A
B
C
D
O
3
4
∠1与∠3的和是180°。
图中还有其他的角也构成互为补角的关系吗?
类似地,如果两个角的和是90° ,那么称这两个角互为余角。
注意:互余与互补是指两个角之间的数量关系,与它们的位置无关。
观察·思考
例2 在数学课上,老师让同学们画对顶角(∠1与∠2),下面作图正确的是( )
D
如左图,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2。将左图简化为右图,ON与DC相交所成的∠DON和∠CON都等于90°,且∠1=∠2。
思考·交流
(1)请在图中找出互为补角和互为余角的角,并说说你的理由。
互余的角:∠1与∠3, ∠2与∠4, ∠1与∠4, ∠2与∠3。
互补的角:∠1和∠AOC,∠2和∠BOD,∠DON与∠CON,
∠1和∠DOB,∠2和∠AOC。
思考·交流
(2)∠3与∠4的大小有什么关系?∠AOC与∠BOD呢?你能说明理由吗?与同伴进行交流。
因为∠3=90°-∠1,∠4=90°-∠2,
而∠1=∠2,
所以∠3=∠4。
思考·交流
因为∠AOC=∠3+90°,∠BOD=∠4+90°,
而∠3=∠4,
所以∠AOC=∠BOD。
因为∠1=∠2,
∠1+∠AOC=180°,∠2+∠BOD=180 ,
所以 ∠AOC= ∠BOD。
补角的性质:同角(或等角)的补角相等。
几何语言:
思考·交流
因为∠1=∠2,
∠1+∠3=90°,∠2+∠4=90°,
所以 ∠3= ∠4。
余角的性质:同角(或等角)的余角相等。
几何语言:
思考·交流
∠1和∠2也是直线AB,CD相交得到的,它们不仅有一个公共顶点O,还有一条公共边OA,像这样的两个角叫作邻补角。
∠2与∠3,∠3与∠4,∠1与∠4都是邻补角。
A
B
C
D
O
1
2
3
4
邻补角的性质:邻补角互补,即互为邻补角的两个角之和为180°。
探索·交流
知识梳理
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
小结·反思
1.同一平面内两线的位置关系:
2.对顶角及其性质:
(1)对顶角的两边互为反向延长线,其实质是:对顶角是两直
线相交所成的没有公共边的两个角。
(2)性质:对顶角相等。
3.余角、补角及其性质
(1)如果两个角的和为90°,那么称这两个角互为余角;如果
两个角的和为180°,那么称这两个角互为补角。
(2)性质:同角或等角的补角相等,同角或等角的补角相等。
相交和平行。
同课章节目录
