9.2轴对称同步练习（含解析）

中小学教育资源及组卷应用平台
9.2轴对称
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列各组图形中，两个图案是轴对称的有（ ）
A．①③④ B．①③ C．①②③ D．①②③④
2．要在一块长方形的空地上修建一个花坛，要求花坛图案为轴对称图形，且恰好有两条对称轴，则下列图形中符合设计要求的有（ ）
A．4个 B．3个 C．2个 D．1个
3．下列轴对称图形中，对称轴最少的图形是（　　）
A． B． C． D．
4．中国新能源汽车市场快速增长，成为中国汽车行业的一抹亮色．以下的新能源汽车品牌标志中，不是轴对称图形的是（ ）
A． B． C． D．
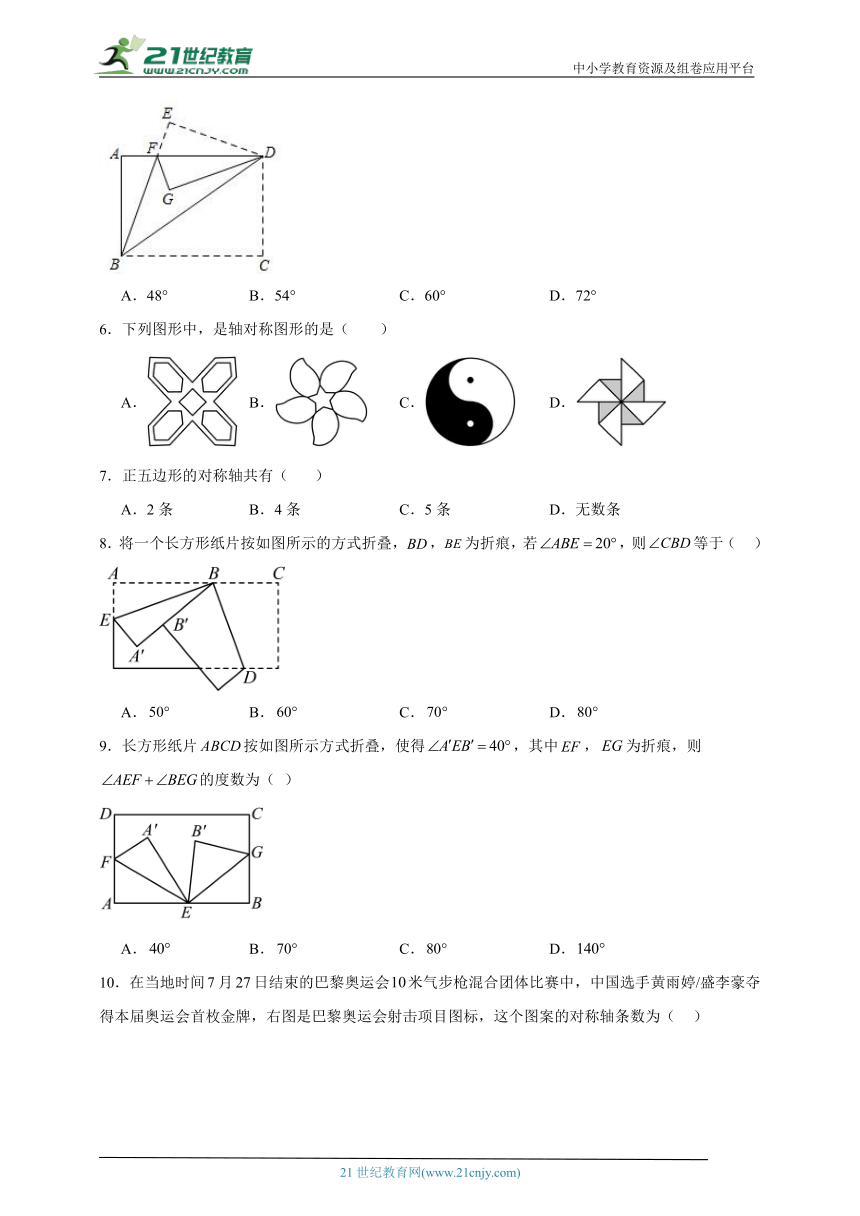
5．如图，将长方形ABCD沿对角线BD对折，点C落在点E处，BE与AD交于F点，再将沿DF折叠，点E落到点G处，此时DG为的角平分线，则的度数为（ ）
A．48° B．54° C．60° D．72°
6．下列图形中，是轴对称图形的是（　　）
A． B． C． D．
7．正五边形的对称轴共有（ ）
A．2条 B．4条 C．5条 D．无数条
8．将一个长方形纸片按如图所示的方式折叠，，为折痕，若，则等于（ ）
A． B． C． D．
9．长方形纸片按如图所示方式折叠，使得，其中，为折痕，则的度数为（ ）
A． B． C． D．
10．在当地时间月日结束的巴黎奥运会米气步枪混合团体比赛中，中国选手黄雨婷/盛李豪夺得本届奥运会首枚金牌，右图是巴黎奥运会射击项目图标，这个图案的对称轴条数为（ ）
A． B． C． D．
11．一条两边沿互相平行的围巾按图所示折叠，已知∠DAB-∠ABC=8°，且DFCG，则∠DAB+2∠ABC=（　　）度．
A．130 B．131 C．132 D．133
12．如图，把一张矩形纸片ABCD按所示方法进行两次折叠，得到△ECF．若BC＝1，则△ECF的周长为（　　）
A． B． C． D．
二、填空题
13．我们知道圆、线段都是轴对称图形，请再写出一个是轴对称图形的几何图形名称 ．
14．在线段、等腰三角形、直角三角形和圆这四个图形中，是轴对称图形的有 个．
15．习近平主席提到“人不负青山，青山定不负人”，一语道出“人与自然和谐共生”的至简大道．如图有关环保的四个图形中，不是轴对称图形的是 ，（填序号）
　　　 　　
16．如图（1）所示是长方形纸带，，将纸带沿折叠成图（2），再沿折叠成图（3），则图（3）中的的度数是 ．

17．如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为、，若CD//BE，，则的度数是 ．
三、解答题
18．如图，和关于直线l对称，已知，，DF＝5．求∠F的度数和AC的长．
19．如图，长方形中，，E为边上一点，将长方形沿折叠（为折痕），使点B与点F重合，平分交于点G，过点G作交于点H．

(1)求证：；
(2)若，求的度数．
20．如图1，将长方形纸片沿着翻折，使得点，分别落在点，位置．如图2，在第一次翻折的基础上再次将纸片沿着翻折，使得点恰好落在延长线上的点处．
(1)若，求的度数；
(2)若，试用含的式子表示，并说明理由．
21．平移和轴对称是数学中两种重要的图形运动．
(1)平移
①把笔尖放在数轴的原点处，先向负方向移动5个单位长度，再向正方向移动2个单位长度，这时笔尖的位置表示什么数？用算式表示以上过程及结果是（ ）．
A． B．
C． D．
②一机器人从原点O开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳，当它跳2022次时，落在数轴上的点表示的数是________．
(2)轴对称
若对折纸条，表示-1的点与表示3的点重合，则表示2022的点与表示________的点重合．
(3)若数轴上M，N两点对应的数分别表示为m，n，将点M向正方向平移5个单位得到，将点N向负方向平移3个单位长度得到，且，两点经对折后重合，对折的中间点表示的数为多少？（用含有m，n的式子表示）
22．（1）如图1，将一张三角形纸片沿着折叠，使点C落在边上的处，若，则__________，其中是的__________线．
（2）如图2，将一张三角形纸片沿着折叠（点D，E分别在边，上），点A落在点的位置，若，则__________．
（3）如图3，将长方形纸片沿着和折叠成图示的形状，和重合．
①求的度数．
②如果，求的度数．

23．如图，的边关于的对称线段是，边关于的对称线段是，连接．若点落在所在的直线上，，求的度数．
24．如图，和关于直线对称，和关于直线对称．

(1)画出直线；
(2)直线与相交于点，试探究与直线，所夹锐角的数量关系．
《9.2轴对称》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C B A C C B B
题号 11 12
答案 B A
1．B
【分析】此题考查轴对称的定义：两个图形，沿着一条直线翻折后，去其中的一个图形与另一个图形完全重合，则这两个图形关于这条直线成轴对称，根据定义依次判断即可．
【详解】解：①③是轴对称，②④不是轴对称，
故选：B．
2．B
【分析】本题考查了轴对称的知识，解题的关键是熟练掌握轴对称图形的概念：把一个图形沿着某条直线折叠，能够与原图形重合；结合各图形，逐一进行判断即可完成求解．
【详解】四个图形均为轴对称图形，其中从左往右数第1、2、4图有两条对称轴，第3个图形只有一条对称轴．
故选：B．
3．B
【分析】此题考查轴对称图形，正确找出各个图形的对称轴是解题的关键．如果一个图形沿着一条直线对折，两侧的图形能完全重合，这个图形就是轴对称图形．折痕所在的这条直线叫做对称轴．根据对称轴的概念、结合图形分别找出各个图形的对称轴，即可得到答案．
【详解】解：A．图中有四条对称轴；
B．图中有三条对称轴；
C．图中有四条对称轴；
D．图中有四条对称轴；
综上分析可知：对称轴最少的图形是B选项中的图形．
故选：B．
4．C
【分析】根据轴对称图形的定义判断选择即可．本题考查了轴对称图形即沿着某条直线折叠，直线两旁的部分完全重合；熟练掌握定义是解题的关键．
【详解】
A、∵是轴对称图形，
∴不符合题意；
B、∵是轴对称图形，
∴不符合题意；
C、∵不是轴对称图形，
∴符合题意；
D、∵是轴对称图形，，
∴不符合题意；
故选C．
5．B
【分析】根据折叠的性质可得∠BDC=∠BDE，∠EDF=∠GDF，由角平分线的定义可得∠GDF=∠BDG，然后根据矩形的内角为90°就可以求出答案．
【详解】解：由折叠可知，∠BDC=∠BDE，∠EDF=∠GDF，
∵DG平分∠ADB，
∴∠GDF=∠BDG，
∴∠EDF=∠BDG，
∴∠BDE=∠EDF+∠GDF+∠BDG=3∠GDF，
∴∠BDC=∠BDE=3∠GDF，
∠BDA=∠GDF+∠BDG=2∠GDF，
∵∠BDC+∠BDA=90°=3∠GDF+2∠GDF=5∠GDF，
∴∠GDF=18°．
∴∠BDE=3∠GDF=54°．
故选：B．
【点睛】本题考查的是角的运算及角平分线的定义，正确掌握折叠的性质是解决本题的关键．
6．A
【分析】本题考查轴对称图形，根据轴对称图形的定义，一个图形沿着一条直线折叠，直线两旁的部分能够相互重合，那么这个图形叫做轴对称图形，逐项判断即可．
【详解】解：A、该图形是轴对称图形，符合题意；
B、该图形不是轴对称图形，不符合题意；
C、该图形不是轴对称图形，不符合题意；
D、该图形不是轴对称图形，不符合题意；
故选：A．
7．C
【分析】根据轴对称图形的性质判断即可．
【详解】解：如图：
一个正五边形的对称轴共有5条．
故选：C．
【点睛】本题考查了轴对称的性质，正五边形过每个顶点垂直对边的直线都是正五边形的对称轴．
8．C
【分析】本题考查了角的计算，折叠对称，解题的关键是熟练掌握角的计算，图形的折叠对称的性质．
利用折叠对称的关系，角的和差关系，求出的值．
【详解】解：根据题意可知，，，
，
故选：C
9．B
【分析】本题考查翻折变换，掌握折叠的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
由折叠可得，，再根据进行计算即可．
【详解】解：由折叠可得，，
，
，
，
故选：B．
10．B
【分析】本题考查了轴对称图形对称轴，根据正方形有四条对称轴即可判断求解，正确识图是解题的关键．
【详解】解：∵图标中间是一个正方形，而正方形有四条对称轴，圆有无数条对称轴，
∴这个图案的对称轴条数为，
故选：．
11．B
【分析】将围巾展开，利用折叠的性质和平行线的性质推导即可．
【详解】解 ：如图，将围巾展开，
则∠ADM =∠ADF，∠KCB=∠BCN，
设∠ABC = x，则∠DAB=x+8°，
∵CDAB，
∴∠ADM=∠DAB=∠ADF=x+8°，
∵DFCG，
∴∠FDC=∠KCG=2x，
∵∠FDC + ∠FDM = 180°，
即2x +2（x+ 8°） = 180°，
解得 x=41°，
∴∠DAB+2∠ABC=（x+ 8°）+2x= 131°．
故选：B．
【点睛】本题考查折叠的性质与平行线的性质，根据∠FDC + ∠FDM = 180°列方程是解题的关键．
12．A
【分析】第一次翻折可得，EM=1，∠ADM=∠EDM=45°，第二次折叠，可得，，由∠DCN=45°，可得，则，再求的周长即可．
【详解】如图，
第一次折叠，如图②，
，
，
，
由折叠的性质，，
，
第二次折叠，如图③，，，
，
，
，
，
，
，
的周长，
故选：A．
【点睛】本题考查翻折的性质，熟练掌握翻折的性质，对应两次翻折求出∠EDM=45°是解题的关键．
13．正方形（答案不唯一）
【分析】根据轴对称图形的概念求解．
【详解】解：写出一个是轴对称图形的几何图形，如正方形（答案不唯一）．
故答案为：正方形（答案不唯一）．
【点睛】本题考查轴对称图形的意义．在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，这条直线就是其对称轴．理解轴对称图形的意义是解题的关键．
14．3
【分析】此题主要考查了轴对称图形，关键是掌握如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴；
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可；
【详解】解：线段、等腰三角形和圆都能找到一条(或多条) 直线，使图形沿一条直线折叠直线两旁的部分能够互相重合，所以是轴对称图形；
直角三角形(等腰直角三角形除外) 不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
所以是轴对称图形的有3个，
故答案为：3．
15．①③④
【分析】根据轴对称图形的定义，即可进行解答．
【详解】解：①不是轴对称图形，符合题意；
②是轴对称图形，不符合题意；
③不是轴对称图形，符合题意；
④不是轴对称图形，符合题意；
综上：不是轴对称图形的有①③④；
故答案为：①③④．
【点睛】本题主要考查了轴对称图形的定义，解题的关键是掌握轴对称图形：一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．
16．/105度
【分析】本题考查了翻折变换以及长方形形的性质，解题的关键是找出．解决该题型题目时，根据翻折变换找出相等的边角关系是关键．由矩形的性质可知，由此可得出，再根据翻折的性质可知每翻折一次减少一个的度数，由此即可算出度数．
【详解】解：四边形为长方形，
，
．
由翻折的性质可知：
图2中，，，
图3中，．
故选：
17．/30度
【分析】利用平行线的性质以及翻折不变性即可得到∠1=∠3=∠4=15°，进而得出∠2=30°．
【详解】解：如图，分别延长EB、DB到F，G，
由于纸带对边平行，
∴∠1=∠4=15°，
∵纸带翻折，
∴∠3=∠4=15°，
∴∠DBF=∠3+∠4=30°，
∵CDBE，
∴∠2=∠DBF=30°．
故答案为：30°．
【点睛】本题考查平行线的性质和折叠的性质，解题的关键是熟练掌握：两直线平行，内错角相等．
18．；AC的长为5
【分析】根据轴对称的性质解答即可．
【详解】∵和关于直线l对称，，，DF＝5
∴，AC=5
在中，，
∴
【点睛】本题考查了轴对称的性质．
19．(1)见解析
(2)．
【分析】（1）根据折叠的性质得，根据角平分线定义及垂直的定义得，最后由平行的判定可得结论；
（2）由余角的性质得，然后根据平行线的性质可得答案．
【详解】（1）证明：∵长方形沿折叠，
∴，
∵平分交于点G，
∴，
∵，
∴，
∴，
∵，
∴；
（2）解：∵，
∴，
∵长方形中，，
∴，
∵，
∴．
【点睛】此题考查了折叠问题及平行线的性质，掌握平行线的判定和性质是解题的关键．
20．(1)40°
(2)，理由见解析
【分析】（1）根据翻折变换的性质可得：∠EMN=∠BMN=70°，再运用邻补角互补即可求得答案；
（2）由翻折可得：，∠BMN=∠QMN，再运用邻补角互补即可求得答案．
【详解】（1）解∶根据题意得：∠EMN=∠BMN=70°，
∴∠BME=140°，
∴∠AME=180°-∠BME=40°；
（2）解：，理由如下：
根据题意得：，∠BMN=∠QMN，
∴，
∴∠AMQ=180°-∠QMN-∠BMN=．
【点睛】本题考查了几何变换——翻折的性质，邻补角互补等，熟练掌握翻折的性质是解题关键．
21．(1)①C；②-1011
(2)-2020
(3)
【分析】（1）①根据数轴上的点的位置，列出算式，即可；②根据规律，每跳跃两次，点从原点向左平移1个单位，跳2022次是点从原点向左平移1011个单位，再计算即可求得；
（2）根据翻折的特征，左右两点到折痕的距离相等，即可求解；
（3）先根据平移表示出点与点所对应的数，再利用翻折后左右两点到折痕的距离相等求解即可．
【详解】（1）解：①根据数轴上的实数和点的平移规律，
可知：，
故选：C；
②由题意可知：每跳跃两次，点从原点向左平移1个单位，
∴当它跳2022次时，点从原点向左平移1011个单位，
∴此时落在数轴上的点表示的数是0-1011=-1011；
故答案为：﹣1011
（2）解：∵对折纸条，表示-1的点与表示3的点重合，
∴折痕的位置点是，
∴2022-1=2021，1-2021=-2020，
即表示2022的点与表示﹣2020的点重合；
故答案为：﹣2020
（3）解：∵M，N两点对应的数分别表示为m，n，
将点M向正方向平移5个单位得到，将点N向负方向平移3个单位长度得到，
∴点所表示的数为：，点所表示的数为：，
∴与对折后的中间点所表示的数是 ．
【点睛】本题考查了数轴、有理数的加减混合运算、平移、折叠等知识，理解题意，灵活应用所学知识是解决问题的关键．
22．（1），角平分；（2）；（3），．
【分析】（1）根据折叠的性质可得，即可求解；
（2）根据三角形的内角和定理可得，根据折叠的性质可得，进而可求出；
（3）①根据折叠的性质可得，，因此；由①的结论代入即可求解．
【详解】（1）根据折叠可得，
∴是的平分线，。
故答案为：，角平分
（2）∵，
∴，
由折叠可得，，
∴，
∴．
故答案为：
（3）①由折叠，知，，
∴．
②由①知，，
∴．
【点睛】本题考查折叠的性质，三角形的内角和定理，掌握折叠的性质是解题的关键．
23．
【分析】本题主要考查轴对称的性质，及三角形全等的判定及性质，根据对称性可判断出，先求出，再根据对称的性质判断，最后根据即可求解．
【详解】解：如图，连接，设与的交点为O．
因为关于的对称线段是，
所以．
因为，
所以
因为边关于的对称线段是，
所以，
所以，
所以，
所以．
又因为点落在所在的直线上，，
所以，
所以，
所以．
24．(1)见解析
(2)
【分析】本题考查了轴对称作图及性质，解答此题要明确轴对称的性质：1．对称轴是一条直线．2．垂直并且平分一条线段的直线称为这条线段的垂直平分线，或中垂线．线段垂直平分线上的点到线段两端的距离相等．3．在轴对称图形中，对称轴两侧的对应点到对称轴两侧的距离相等．4．在轴对称图形中，对称轴把图形分成完全相等的两份．5．如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．
（1）如答图，连接，画出线段的垂直平分线EF，则直线EF即为所求．
（2）根据对称找到相等的角，然后进行推理．
【详解】（1）解：如图，连接，画出线段的垂直平分线，则直线即为所求．

（2）解：如图，连接，，

因为和关于直线对称，
所以
因为和关于直线对称，
所以，
所以，
即
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)