9.2平移同步练习(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
9.2平移
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
2.小明读了“子非鱼,安知鱼之乐?”后,兴高采烈地利用电脑画出了几幅鱼的图案.由图所示的图案通过平移后得到的图案是( )
A. B. C. D.
3.如图,将向右平移得到,如果四边形的周长是,那么的周长是( )
A. B. C. D.
4.在以下现象中,属于平移的是( )
A.在荡秋千的小朋友 B.湖面上随波摇摆的树叶
C.“天宫一号”绕着地球运动 D.水平传送带上的物体
5.如图,将沿方向平移得到.连接,若,,则的长为( )
A. B. C. D.
6.如图,在△ABC中,边BC在直线MN上,且BC=9cm.将△ABC沿直线MN平移得到△DEF,点B的对应点为E.若平移的距离为3cm,则CE的长为( )
A.3cm B.6cm C.3cm或6cm D.6cm或12cm
7.如图,在直角三角形ABC中,,将三角形ABC沿直线BC向右平移2cm得到三角形DEF,连接AE,有以下结论:①;②;③;④,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.如图是从一块边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,则这块垫片的周长为( )
A.182cm B.191cm C.209cm D.218cm
9.有以下说法:
①△ABC在平移的过程中,对应线段一定相等;
②△ABC在平移过程中,对应线段一定平行;
③△ABC在平移过程中,周长保持不变;
④△ABC在平移过程中,对应角分别相等.
正确的是( )
A.①②③④ B.①③④ C.②③④ D.①②③
10.如图,在一块长14m、宽6m的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移3m就是它的右边线,则绿化区的面积是( )
A. B. C. D.
11.如图,长方形中,,,现将该长方形沿方向平移.得到长方形,若重叠部分的面积为,则长方形向右平移的距离为( )
A. B. C. D.
12.将图①中周长为40的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图②的方式放入周长58的长方形中,则没有覆盖的阴影部分的周长为 ( )
A.44 B.48 C.46 D.50
二、填空题
13.如图,把一个三角形纸板的一边紧靠数轴平移,点平移的距离为 .
14.如图所示,某住宅小区内有一长方形地块,长为18m,宽为12m.想在长方形地块内修筑同样宽的两条“之”字路,余下部分绿化,道路的宽为2米,则绿化的面积为 .
15.如图,长方形中,横面阴影部分是长方形,另一阴影部分为平行四边形,根据图中数据,其中空白部分面积的和是 .
16.如图,将三角形水平向右平移得到三角形,,两点的距离为1,,,则
(1)与的关系式为 , ;
(2) (度);
(3) .
17.如图,有一块长为a米宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草场的面积为m2,则 .
三、解答题
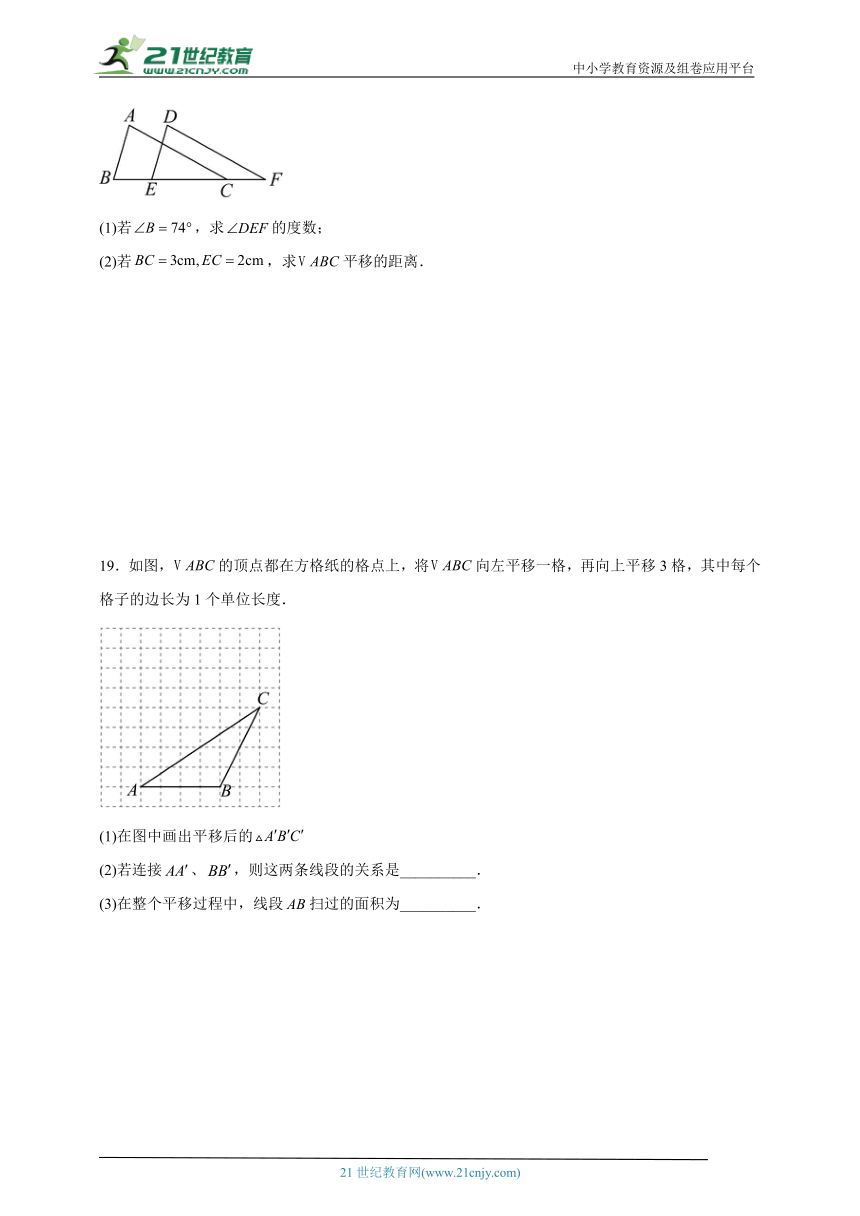
18.如图,将沿的方向平移得到.
(1)若,求的度数;
(2)若,求平移的距离.
19.如图,的顶点都在方格纸的格点上,将向左平移一格,再向上平移3格,其中每个格子的边长为1个单位长度.
(1)在图中画出平移后的
(2)若连接、,则这两条线段的关系是__________.
(3)在整个平移过程中,线段扫过的面积为__________.
20.如图,将三角形经过平移后得到三角形,其中点平行移动到了点.画出平行移动后得到的三角形.
21.如图,在中,,将沿的方向平移得到,其中.
(1)求的长;
(2)若,求的度数.
22.如图,在边长为1的小正方形组成的网格中,将平移得到,连接,.
(1)根据题意,补全图形;
(2)图中和的数量关系是 ;
(3)在上画出一点P,使得.
23.如图所示,已知在中,,把沿方向平移得到.问:
(1)图中与相等的角有多少个?
(2)图中的平行线共有多少对?请分别写出来.
(3)的值是多少?
24.动手操作:
(1)如图1,在的网格中,每个小正方形的边长为1,将线段向右平移,得到线段,连接.
①线段平移的距离是___________;
②四边形的面积是___________;
(2)如图2,在的网格中,将向右平移3个单位长度得到.
③画出平移后的;
④连接,多边形的面积是___________
拓展延伸:(3)如图3,在一块长为米,宽为米的长方形草坪上,修建一条宽为米的小路(小路宽度处处相同),直接写出剩下的草坪面积是___________.
《9.2平移》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C D B D D D B B
题号 11 12
答案 B B
1.B
【分析】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小.根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是B.
【详解】
解:A、图形的平移只改变图形的位置,图形位置没变化,不是平移变换,故不符合题意;
B、图形的平移只改变图形的位置,而不改变图形的形状和大小,故符合题意;
C、图形的平移只改变图形的位置,图形位置没变化,不是平移变换,故不符合题意;
D、图形的平移只改变图形的位置,图形位置没变化,不是平移变换,故不符合题意.
故选:B.
2.D
【分析】本题考查图形的平移,根据平移的性质,平移后的图形的大小,形状和方向均不发生改变,只有位置发生变化,进行判断即可.
【详解】解:∵平移后的图形的大小,形状和方向均不发生改变,
∴只有选项D是通过题干图案平移得到的,
故选D.
3.C
【分析】本题考查了平移的性质,根据平移的性质可得,,然后判断出四边形的周长的周长,然后代入数据计算即可得解.能熟练利用平移的性质进行求解是解题的关键.
【详解】解:∵将向右平移得到,
,
,
∴,
,
的周长为:
,
故选:C.
4.D
【分析】根据平移的性质,对选项进行一一分析,排除错误答案.
【详解】解:A.在荡秋千的小朋友是旋转运动,不是平移;
B.湖面上随波摇摆的树叶不是平移;
C.“天宫一号”绕着地球运动是旋转,不是平移;
D.水平传送带上的物体是平移;
故选:D.
【点睛】本题考查图形的平移变换.图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,以致选错.
5.B
【分析】本题主要考查了平移的性质,根据平移的性质得到, 再根据线段的和差关系求解即可.
【详解】解:由平移的性质可得,
∴,
故选:B.
6.D
【分析】根据平移的性质求出BE,分△ABC沿直线MN向右平移、△ABC沿直线MN向左平移两种情况计算,得到答案.
【详解】解:由平移的性质可知,BE=3cm,
当△ABC沿直线MN向右平移得到△DEF时,CE=BC-BE=9-3=6(cm),
当△ABC沿直线MN向左平移得到△DEF时,CE=BC+BE=9+3=12(cm),
∴CE的长为6cm或12cm,
故选:D.
【点睛】本题考查的是平移的性质,根据平移的性质求出BE的长是解题的关键.
7.D
【分析】利用平移的性质可得,即可判断①④的正确性,由,即可判断③的正确性,再根据平行线的性质即可判断②的正确性 .
【详解】解:∵△ABC沿直线BC向右平移得到△DEF,
∴,,故①正确
∴,
∴,故②正确
∵,
∴,故③正确
∵△ABC沿直线BC向右平移得到△DEF,
∴,故④正确
故选:D.
【点睛】本题考查了平行线的判定与性质,平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等,合理的运用性质是解答此题的关键.
8.D
【分析】根据平移的思想进行求解即可.
【详解】解:在正方形中CD=BC=50cm,
由平移可知,
EF+GH+AB=CD=50cm,
AH+ED=BC+FG=50+9=59cm,
∴这块垫片的周长为50+50+59×2=218cm.
故选:D.
【点睛】本题考查了平移的实际问题,通过平移将垫片的周长与正方形的周长联系是解决问题的关键.
9.B
【分析】根据平移的性质判断即可.
【详解】解:①△ABC在平移的过程中,对应线段一定相等,正确;
②△ABC在平移过程中,对应线段平行或在一条直线上,所以原说法不正确;
③△ABC在平移过程中,周长保持不变,正确;
④△ABC在平移过程中,对应角分别相等,正确.
故选:B.
【点睛】本题考查平移的性质,关键是利用了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
10.B
【分析】根据平移的性质可得,绿化部分可看作是长为(14-3)m,宽为6m的矩形,然后根据矩形面积公式进行计算即可解答.
【详解】解:由题意得:
(14-3)×6
=11×6
=66(m2),
∴绿化区的面积是66 m2,
故选:B.
【点睛】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
11.B
【分析】根据重叠部分的面积求出的长,然后根据平移的性质可知,平移的距离为线段与线段的差,即可得到答案.
【详解】解:重叠部分为矩形,面积为,,
,
,
,
故选B.
【点睛】本题考查了平移的性质,矩形的性质,解题关键是确定平移的距离为线段与线段的差.
12.B
【分析】此题考查整式加减的应用,平移的性质,利用平移的性质将不规则图形变化为规则图形进而求解,解题的关键是设出未知数,列代数式表示各线段进而解决问题.
设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为,4号正方形的边长为,5号长方形的长为,宽为,根据图1中长方形的周长为40,求得,根据图中长方形的周长为58,求得,根据平移得:没有覆盖的阴影部分的周长为四边形的周长,计算即可得到答案.
【详解】解:设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为,4号正方形的边长为,5号长方形的长为,宽为,
由图1中长方形的周长为40,可得,,
解得:,
如图,∵图2中长方形的周长为58,
∴,
∴,
根据平移得:没有覆盖的阴影部分的周长为四边形的周长,
∴
;
故选:B.
13.5
【分析】此题主要考查了图形的平移变换的性质,数轴上两点间的距离,熟练掌握平移变换的性质,理解数轴上两点间的距离是解答此题的关键.观察得出两个三角形平移的距离为5个单位长度,然后根据平移的性质可得出答案.
【详解】解:如图,
的顶点在数轴上所对应的数为,的顶点在数轴上所对应的数为0,且点为点平移后的对应点,
平移了个单位长度,
又点和点是平移前后的对应点,
根据平移的性质得:点平移的距离为5个单位长度.
故答案为:5.
14.160
【分析】利用平移把不规则的图形变为规则图形,如此一来,所有绿化面积之和就变为了(18 2)×(12 2)m2,进而即可求出答案.
【详解】解:利用平移可得,所有绿化面积之和为(18 2)×(12 2)=160(m2)
答:绿化的面积为160m2.
故答案为:160.
【点睛】此题主要考查了生活中的平移现象,这类题目体现了数形结合的思想,需利用平移把不规则的图形变为规则图形,进而即可列出式子求出答案.
15.36
【分析】先求出矩形的面积,再分别求出长方形阴影部分和平行四边形阴影部分的面积,两块交叉的部分面积,根据图形求出即可,或根据平移的性质求得空白部分的面积.
【详解】解:∵长方形的面积是,
长方形阴影部分的面积是:,
平行四边形阴影部分的面积是:,
两块交叉的部分面积是,
∴图中空白部分的面积是:.
解法二:根据平移的性质,可得空白部分的面积等于长为,宽为的长方形的面积,则面积为36.
故答案为:36.
【点睛】本题考查了图形的面积计算,注意:两块阴影部分的交叉处的面积是1,题目比较好,但是一道比较容易出错的题目.
16.
【分析】(1)根据平移前后对应线段平行(或在同一直线上)且相等即可解答;
(2)根据平移前后对应线段平行得出,再利用平行线的性质和对顶角相等求解即可;
(3)根据平移前后对应点的连线平行(或在同一直线上)且相等得出即可求出答案.
【详解】(1)∵三角形水平向右平移得到三角形,
∴与的关系式为:,;
(2)设与相交于点,
∵三角形水平向右平移得到三角形,
∴.
∵,
∴.
∴.
(3)∵三角形水平向右平移得到三角形,,两点的距离为1,
∴.
∵,
∴.
故答案是,;;.
【点睛】本题主要考查了平移的性质,熟练掌握平移前后对应线段平行(或在同一直线上)且相等,对应点的连线平行(或在同一直线上)且相等是解题的关键.
17.
【分析】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.根据小路的左边线向右平移1米能得到它的右边线,可得路的宽度是1米,根据平移,可把路移到左边,再根据长方形的面积公式,可得答案.
【详解】解:依题意有,
解得.
故答案为:.
18.(1)
(2)1cm
【分析】(1)根据平移的性质,得到对应角相等,即可得解;
(2)根据,求出的长,即为平移的距离
【详解】(1)解:将沿的方向平移得到,
∴;
(2)解:∵,
∴,即:平移的距离为1cm.
【点睛】本题考查平移的性质,熟练掌握平移的性质,是解题的关键.
19.(1)见解析
(2)相等且平行
(3)12
【分析】(1)根据平移的方向及距离画图即可;
(2)根据平移的性质:对应点连线平行(或在同一直线上)且相等解答;
(3)线段扫过的图形为平行四边形,根据公式计算面积.
【详解】(1)如图,即为所求;
(2)线段、的关系是相等且平行,
故答案为:相等且平行;
(3)线段扫过的图形为平行四边形,底为4,高为3,故面积为,
故答案为:12.
【点睛】此题考查了平移的性质:平移前后对应的线段平行(或在同一直线上)且相等,对应角相等,对应点连线平行(或在同一直线上)且相等,熟练掌握平移的性质是解题的关键.
20.见解析
【分析】本题考查平移作图,根据点平行移动到了点,得到平移的方向和距离,再根据其找出、的对应点、,顺次连接对应点、、,即可解题.
【详解】解:点向左平移三格,向上平移一格,移动到了点.
三角形也由三角形向左平移三格,向上平移一格得到,
所作三角形如图所示:
21.(1)
(2)
【分析】(1)根据平移的性质求解即可;
(2)根据平移的性质、直角三角形的性质求解即可.
【详解】(1)沿的方向平移得到,
.
,
.
(2)由题可得,
.
【点睛】此题考查了平移的性质、直角三角形的性质,熟练掌握平移的性质、直角三角形的性质是解题的关键.
22.(1)图见解析
(2)互补
(3)见解析
【分析】本题主要考查了平移(作图),平移的性质,平行线的性质等知识点,熟练掌握平移的性质是解题的关键.
(1)根据的位置,确定平移规则,据此画出,再连接,即可;
(2)根据平移的性质即可作答;
(3)根据网格特点,过点作,交于点P,则点P即为所求作.
【详解】(1)解:如图,,,即为所求作;
(2)解:由平移的性质可知:,
∴,
即:和互补,
故答案为:互补;
(3)解:如图,根据网格特点,过点作,交于点P,则点P即为所求作,
理由如下:
∵,
∴,
由平移的性质可知:,
∴.
23.(1)3个,分别是,,
(2)两对,
(3)
【分析】本题考查了平移的性质,解题的关键是理解平移的方向,由图形判断平移的方向和距离.注意结合图形解题的思想.
(1)根据平移前后的两个图形的对应角相等可以得到;
(2)根据平移前后的两对对应点的连线互相平行可以得到;
(3)利用平移的性质求得有关线段的长,然后求其比值即可;
【详解】(1)解:把沿方向平移得到,
,,
,
有3个,分别是,,.
(2)解:根据(1)中原理可得
故有两对,,
(3)解:沿方向平移,
,
,
.
.
24.(1)①;②(2)③见解析,④(3)平方米
【分析】本题考查平移性质的应用、列代数式,熟知网格特点,掌握平移性质是解答的关键.
(1)①根据平移性质和网格特点求解即可;②根据网格特点和平行四边形的面积公式求解即可;
(2)③根据平移性质和网格特点可画出图形;④根据网格特点,三角形的面积公式和长方形的面积公式求解即可;
(3)根据平移性质,可将小路两边的草坪平移,拼凑成一个长米,宽为b米的长方形,再利用长方形的面积公式求解即可.
【详解】(1)解:①根据平移性质,线段平移的距离是;
②根据图形,四边形的面积为:;
故答案为:①;②;
(2)解:③如图所示,即为所求作;
④由图形知,
∴多边形的面积为:
,
故答案为:;
(3)解:由题意得,将小径右侧平移与左侧拼接成一个长方形,
长方形的长米,宽为b米,
则剩下的草坪面积是:,
故答案为:平方米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.2平移
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是( )
A. B.
C. D.
2.小明读了“子非鱼,安知鱼之乐?”后,兴高采烈地利用电脑画出了几幅鱼的图案.由图所示的图案通过平移后得到的图案是( )
A. B. C. D.
3.如图,将向右平移得到,如果四边形的周长是,那么的周长是( )
A. B. C. D.
4.在以下现象中,属于平移的是( )
A.在荡秋千的小朋友 B.湖面上随波摇摆的树叶
C.“天宫一号”绕着地球运动 D.水平传送带上的物体
5.如图,将沿方向平移得到.连接,若,,则的长为( )
A. B. C. D.
6.如图,在△ABC中,边BC在直线MN上,且BC=9cm.将△ABC沿直线MN平移得到△DEF,点B的对应点为E.若平移的距离为3cm,则CE的长为( )
A.3cm B.6cm C.3cm或6cm D.6cm或12cm
7.如图,在直角三角形ABC中,,将三角形ABC沿直线BC向右平移2cm得到三角形DEF,连接AE,有以下结论:①;②;③;④,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.如图是从一块边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,则这块垫片的周长为( )
A.182cm B.191cm C.209cm D.218cm
9.有以下说法:
①△ABC在平移的过程中,对应线段一定相等;
②△ABC在平移过程中,对应线段一定平行;
③△ABC在平移过程中,周长保持不变;
④△ABC在平移过程中,对应角分别相等.
正确的是( )
A.①②③④ B.①③④ C.②③④ D.①②③
10.如图,在一块长14m、宽6m的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移3m就是它的右边线,则绿化区的面积是( )
A. B. C. D.
11.如图,长方形中,,,现将该长方形沿方向平移.得到长方形,若重叠部分的面积为,则长方形向右平移的距离为( )
A. B. C. D.
12.将图①中周长为40的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形,并将它们按图②的方式放入周长58的长方形中,则没有覆盖的阴影部分的周长为 ( )
A.44 B.48 C.46 D.50
二、填空题
13.如图,把一个三角形纸板的一边紧靠数轴平移,点平移的距离为 .
14.如图所示,某住宅小区内有一长方形地块,长为18m,宽为12m.想在长方形地块内修筑同样宽的两条“之”字路,余下部分绿化,道路的宽为2米,则绿化的面积为 .
15.如图,长方形中,横面阴影部分是长方形,另一阴影部分为平行四边形,根据图中数据,其中空白部分面积的和是 .
16.如图,将三角形水平向右平移得到三角形,,两点的距离为1,,,则
(1)与的关系式为 , ;
(2) (度);
(3) .
17.如图,有一块长为a米宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草场的面积为m2,则 .
三、解答题
18.如图,将沿的方向平移得到.
(1)若,求的度数;
(2)若,求平移的距离.
19.如图,的顶点都在方格纸的格点上,将向左平移一格,再向上平移3格,其中每个格子的边长为1个单位长度.
(1)在图中画出平移后的
(2)若连接、,则这两条线段的关系是__________.
(3)在整个平移过程中,线段扫过的面积为__________.
20.如图,将三角形经过平移后得到三角形,其中点平行移动到了点.画出平行移动后得到的三角形.
21.如图,在中,,将沿的方向平移得到,其中.
(1)求的长;
(2)若,求的度数.
22.如图,在边长为1的小正方形组成的网格中,将平移得到,连接,.
(1)根据题意,补全图形;
(2)图中和的数量关系是 ;
(3)在上画出一点P,使得.
23.如图所示,已知在中,,把沿方向平移得到.问:
(1)图中与相等的角有多少个?
(2)图中的平行线共有多少对?请分别写出来.
(3)的值是多少?
24.动手操作:
(1)如图1,在的网格中,每个小正方形的边长为1,将线段向右平移,得到线段,连接.
①线段平移的距离是___________;
②四边形的面积是___________;
(2)如图2,在的网格中,将向右平移3个单位长度得到.
③画出平移后的;
④连接,多边形的面积是___________
拓展延伸:(3)如图3,在一块长为米,宽为米的长方形草坪上,修建一条宽为米的小路(小路宽度处处相同),直接写出剩下的草坪面积是___________.
《9.2平移》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C D B D D D B B
题号 11 12
答案 B B
1.B
【分析】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小.根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是B.
【详解】
解:A、图形的平移只改变图形的位置,图形位置没变化,不是平移变换,故不符合题意;
B、图形的平移只改变图形的位置,而不改变图形的形状和大小,故符合题意;
C、图形的平移只改变图形的位置,图形位置没变化,不是平移变换,故不符合题意;
D、图形的平移只改变图形的位置,图形位置没变化,不是平移变换,故不符合题意.
故选:B.
2.D
【分析】本题考查图形的平移,根据平移的性质,平移后的图形的大小,形状和方向均不发生改变,只有位置发生变化,进行判断即可.
【详解】解:∵平移后的图形的大小,形状和方向均不发生改变,
∴只有选项D是通过题干图案平移得到的,
故选D.
3.C
【分析】本题考查了平移的性质,根据平移的性质可得,,然后判断出四边形的周长的周长,然后代入数据计算即可得解.能熟练利用平移的性质进行求解是解题的关键.
【详解】解:∵将向右平移得到,
,
,
∴,
,
的周长为:
,
故选:C.
4.D
【分析】根据平移的性质,对选项进行一一分析,排除错误答案.
【详解】解:A.在荡秋千的小朋友是旋转运动,不是平移;
B.湖面上随波摇摆的树叶不是平移;
C.“天宫一号”绕着地球运动是旋转,不是平移;
D.水平传送带上的物体是平移;
故选:D.
【点睛】本题考查图形的平移变换.图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,以致选错.
5.B
【分析】本题主要考查了平移的性质,根据平移的性质得到, 再根据线段的和差关系求解即可.
【详解】解:由平移的性质可得,
∴,
故选:B.
6.D
【分析】根据平移的性质求出BE,分△ABC沿直线MN向右平移、△ABC沿直线MN向左平移两种情况计算,得到答案.
【详解】解:由平移的性质可知,BE=3cm,
当△ABC沿直线MN向右平移得到△DEF时,CE=BC-BE=9-3=6(cm),
当△ABC沿直线MN向左平移得到△DEF时,CE=BC+BE=9+3=12(cm),
∴CE的长为6cm或12cm,
故选:D.
【点睛】本题考查的是平移的性质,根据平移的性质求出BE的长是解题的关键.
7.D
【分析】利用平移的性质可得,即可判断①④的正确性,由,即可判断③的正确性,再根据平行线的性质即可判断②的正确性 .
【详解】解:∵△ABC沿直线BC向右平移得到△DEF,
∴,,故①正确
∴,
∴,故②正确
∵,
∴,故③正确
∵△ABC沿直线BC向右平移得到△DEF,
∴,故④正确
故选:D.
【点睛】本题考查了平行线的判定与性质,平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等,合理的运用性质是解答此题的关键.
8.D
【分析】根据平移的思想进行求解即可.
【详解】解:在正方形中CD=BC=50cm,
由平移可知,
EF+GH+AB=CD=50cm,
AH+ED=BC+FG=50+9=59cm,
∴这块垫片的周长为50+50+59×2=218cm.
故选:D.
【点睛】本题考查了平移的实际问题,通过平移将垫片的周长与正方形的周长联系是解决问题的关键.
9.B
【分析】根据平移的性质判断即可.
【详解】解:①△ABC在平移的过程中,对应线段一定相等,正确;
②△ABC在平移过程中,对应线段平行或在一条直线上,所以原说法不正确;
③△ABC在平移过程中,周长保持不变,正确;
④△ABC在平移过程中,对应角分别相等,正确.
故选:B.
【点睛】本题考查平移的性质,关键是利用了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
10.B
【分析】根据平移的性质可得,绿化部分可看作是长为(14-3)m,宽为6m的矩形,然后根据矩形面积公式进行计算即可解答.
【详解】解:由题意得:
(14-3)×6
=11×6
=66(m2),
∴绿化区的面积是66 m2,
故选:B.
【点睛】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
11.B
【分析】根据重叠部分的面积求出的长,然后根据平移的性质可知,平移的距离为线段与线段的差,即可得到答案.
【详解】解:重叠部分为矩形,面积为,,
,
,
,
故选B.
【点睛】本题考查了平移的性质,矩形的性质,解题关键是确定平移的距离为线段与线段的差.
12.B
【分析】此题考查整式加减的应用,平移的性质,利用平移的性质将不规则图形变化为规则图形进而求解,解题的关键是设出未知数,列代数式表示各线段进而解决问题.
设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为,4号正方形的边长为,5号长方形的长为,宽为,根据图1中长方形的周长为40,求得,根据图中长方形的周长为58,求得,根据平移得:没有覆盖的阴影部分的周长为四边形的周长,计算即可得到答案.
【详解】解:设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为,4号正方形的边长为,5号长方形的长为,宽为,
由图1中长方形的周长为40,可得,,
解得:,
如图,∵图2中长方形的周长为58,
∴,
∴,
根据平移得:没有覆盖的阴影部分的周长为四边形的周长,
∴
;
故选:B.
13.5
【分析】此题主要考查了图形的平移变换的性质,数轴上两点间的距离,熟练掌握平移变换的性质,理解数轴上两点间的距离是解答此题的关键.观察得出两个三角形平移的距离为5个单位长度,然后根据平移的性质可得出答案.
【详解】解:如图,
的顶点在数轴上所对应的数为,的顶点在数轴上所对应的数为0,且点为点平移后的对应点,
平移了个单位长度,
又点和点是平移前后的对应点,
根据平移的性质得:点平移的距离为5个单位长度.
故答案为:5.
14.160
【分析】利用平移把不规则的图形变为规则图形,如此一来,所有绿化面积之和就变为了(18 2)×(12 2)m2,进而即可求出答案.
【详解】解:利用平移可得,所有绿化面积之和为(18 2)×(12 2)=160(m2)
答:绿化的面积为160m2.
故答案为:160.
【点睛】此题主要考查了生活中的平移现象,这类题目体现了数形结合的思想,需利用平移把不规则的图形变为规则图形,进而即可列出式子求出答案.
15.36
【分析】先求出矩形的面积,再分别求出长方形阴影部分和平行四边形阴影部分的面积,两块交叉的部分面积,根据图形求出即可,或根据平移的性质求得空白部分的面积.
【详解】解:∵长方形的面积是,
长方形阴影部分的面积是:,
平行四边形阴影部分的面积是:,
两块交叉的部分面积是,
∴图中空白部分的面积是:.
解法二:根据平移的性质,可得空白部分的面积等于长为,宽为的长方形的面积,则面积为36.
故答案为:36.
【点睛】本题考查了图形的面积计算,注意:两块阴影部分的交叉处的面积是1,题目比较好,但是一道比较容易出错的题目.
16.
【分析】(1)根据平移前后对应线段平行(或在同一直线上)且相等即可解答;
(2)根据平移前后对应线段平行得出,再利用平行线的性质和对顶角相等求解即可;
(3)根据平移前后对应点的连线平行(或在同一直线上)且相等得出即可求出答案.
【详解】(1)∵三角形水平向右平移得到三角形,
∴与的关系式为:,;
(2)设与相交于点,
∵三角形水平向右平移得到三角形,
∴.
∵,
∴.
∴.
(3)∵三角形水平向右平移得到三角形,,两点的距离为1,
∴.
∵,
∴.
故答案是,;;.
【点睛】本题主要考查了平移的性质,熟练掌握平移前后对应线段平行(或在同一直线上)且相等,对应点的连线平行(或在同一直线上)且相等是解题的关键.
17.
【分析】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.根据小路的左边线向右平移1米能得到它的右边线,可得路的宽度是1米,根据平移,可把路移到左边,再根据长方形的面积公式,可得答案.
【详解】解:依题意有,
解得.
故答案为:.
18.(1)
(2)1cm
【分析】(1)根据平移的性质,得到对应角相等,即可得解;
(2)根据,求出的长,即为平移的距离
【详解】(1)解:将沿的方向平移得到,
∴;
(2)解:∵,
∴,即:平移的距离为1cm.
【点睛】本题考查平移的性质,熟练掌握平移的性质,是解题的关键.
19.(1)见解析
(2)相等且平行
(3)12
【分析】(1)根据平移的方向及距离画图即可;
(2)根据平移的性质:对应点连线平行(或在同一直线上)且相等解答;
(3)线段扫过的图形为平行四边形,根据公式计算面积.
【详解】(1)如图,即为所求;
(2)线段、的关系是相等且平行,
故答案为:相等且平行;
(3)线段扫过的图形为平行四边形,底为4,高为3,故面积为,
故答案为:12.
【点睛】此题考查了平移的性质:平移前后对应的线段平行(或在同一直线上)且相等,对应角相等,对应点连线平行(或在同一直线上)且相等,熟练掌握平移的性质是解题的关键.
20.见解析
【分析】本题考查平移作图,根据点平行移动到了点,得到平移的方向和距离,再根据其找出、的对应点、,顺次连接对应点、、,即可解题.
【详解】解:点向左平移三格,向上平移一格,移动到了点.
三角形也由三角形向左平移三格,向上平移一格得到,
所作三角形如图所示:
21.(1)
(2)
【分析】(1)根据平移的性质求解即可;
(2)根据平移的性质、直角三角形的性质求解即可.
【详解】(1)沿的方向平移得到,
.
,
.
(2)由题可得,
.
【点睛】此题考查了平移的性质、直角三角形的性质,熟练掌握平移的性质、直角三角形的性质是解题的关键.
22.(1)图见解析
(2)互补
(3)见解析
【分析】本题主要考查了平移(作图),平移的性质,平行线的性质等知识点,熟练掌握平移的性质是解题的关键.
(1)根据的位置,确定平移规则,据此画出,再连接,即可;
(2)根据平移的性质即可作答;
(3)根据网格特点,过点作,交于点P,则点P即为所求作.
【详解】(1)解:如图,,,即为所求作;
(2)解:由平移的性质可知:,
∴,
即:和互补,
故答案为:互补;
(3)解:如图,根据网格特点,过点作,交于点P,则点P即为所求作,
理由如下:
∵,
∴,
由平移的性质可知:,
∴.
23.(1)3个,分别是,,
(2)两对,
(3)
【分析】本题考查了平移的性质,解题的关键是理解平移的方向,由图形判断平移的方向和距离.注意结合图形解题的思想.
(1)根据平移前后的两个图形的对应角相等可以得到;
(2)根据平移前后的两对对应点的连线互相平行可以得到;
(3)利用平移的性质求得有关线段的长,然后求其比值即可;
【详解】(1)解:把沿方向平移得到,
,,
,
有3个,分别是,,.
(2)解:根据(1)中原理可得
故有两对,,
(3)解:沿方向平移,
,
,
.
.
24.(1)①;②(2)③见解析,④(3)平方米
【分析】本题考查平移性质的应用、列代数式,熟知网格特点,掌握平移性质是解答的关键.
(1)①根据平移性质和网格特点求解即可;②根据网格特点和平行四边形的面积公式求解即可;
(2)③根据平移性质和网格特点可画出图形;④根据网格特点,三角形的面积公式和长方形的面积公式求解即可;
(3)根据平移性质,可将小路两边的草坪平移,拼凑成一个长米,宽为b米的长方形,再利用长方形的面积公式求解即可.
【详解】(1)解:①根据平移性质,线段平移的距离是;
②根据图形,四边形的面积为:;
故答案为:①;②;
(2)解:③如图所示,即为所求作;
④由图形知,
∴多边形的面积为:
,
故答案为:;
(3)解:由题意得,将小径右侧平移与左侧拼接成一个长方形,
长方形的长米,宽为b米,
则剩下的草坪面积是:,
故答案为:平方米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
