9.5三角形的中位线同步练习（含解析）

中小学教育资源及组卷应用平台
9.5三角形的中位线
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，在平行四边形中，与交于点，点是边的中点，，则的长是（ ）
A．0.5 B．1 C．2 D．4
2．如图，在中，，是边的中点，是边上一点，连接，．若平分的周长，则的长为（ ）
A． B． C．4 D．
3．如图，等腰三角形中，，按以下要求作图：①以点A为圆心，任意长为半径作弧，分别交于D,E两点；②分别以点D、E为圆心，以大于的长为半径作弧，两弧交于点F；③作射线，交于点M；④分别以A、B为圆心，以大于的长为半径作弧，两弧分别交于G,H两点；⑤作直线，交于点N，连接．则的长为（ ）
A．2 B．3 C．4 D．6
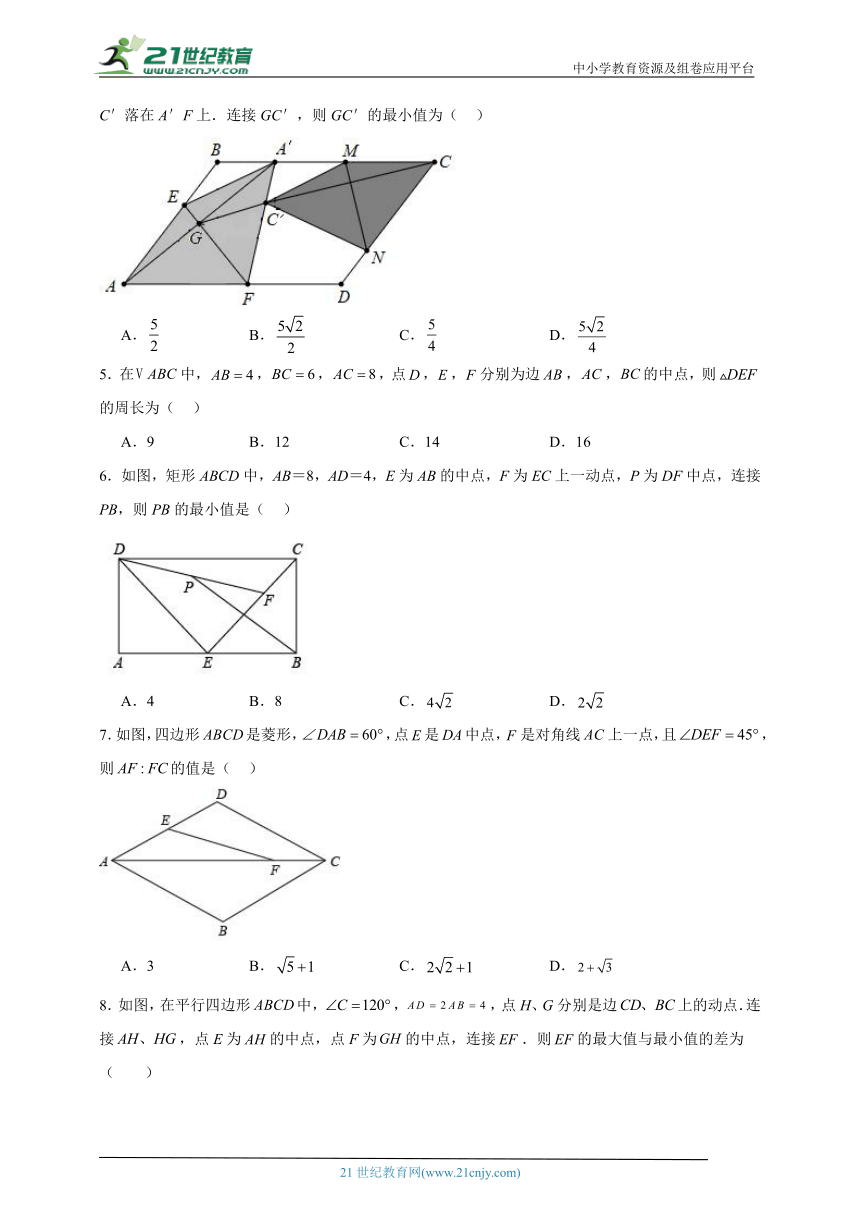
4．如图，在平行四边形ABCD纸片中，∠BAD=45°，AB=10．将纸片折叠，使得点A的对应点A＇落在BC边上，折痕EF交AB、AD、AA＇分别于点E、F、G． 继续折叠纸片，使得点C的对应点C＇落在A＇F上．连接GC＇，则GC＇的最小值为（ ）
A． B． C． D．
5．在中，，，，点，，分别为边，，的中点，则的周长为（ ）
A．9 B．12 C．14 D．16
6．如图，矩形ABCD中，AB＝8，AD＝4，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（ ）
A．4 B．8 C． D．
7．如图，四边形是菱形，，点是中点，是对角线上一点，且，则的值是（ ）
A．3 B． C． D．
8．如图，在平行四边形中，，，点H、G分别是边上的动点．连接，点E为的中点，点F为的中点，连接．则的最大值与最小值的差为（　　）

A．1 B． C． D．
9．如图，平行四边形ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点B，且，，连接OE，下列结论：①；②；③；④，成立的个数有（ ）
A．1个 B．2个 C．3个 D．4个
10．边长为4的正方形中，点、分别是、的中点，连接、，点，分别是、的中点，连接，则的长为( )
A． B．1 C．2 D．
11．如图，在△ABC中，AC=BC，D、E分别是边AB、AC的中点，△ADE≌△CFE，则四边形ADCF一定是（ ）
A．菱形 B．矩形 C．正方形 D．无法确定
12．如图，在中，点D、E、F分别为边、、的中点，分别连结、、、，点O是与的交点，下列结论中，正确的个数是（ ）
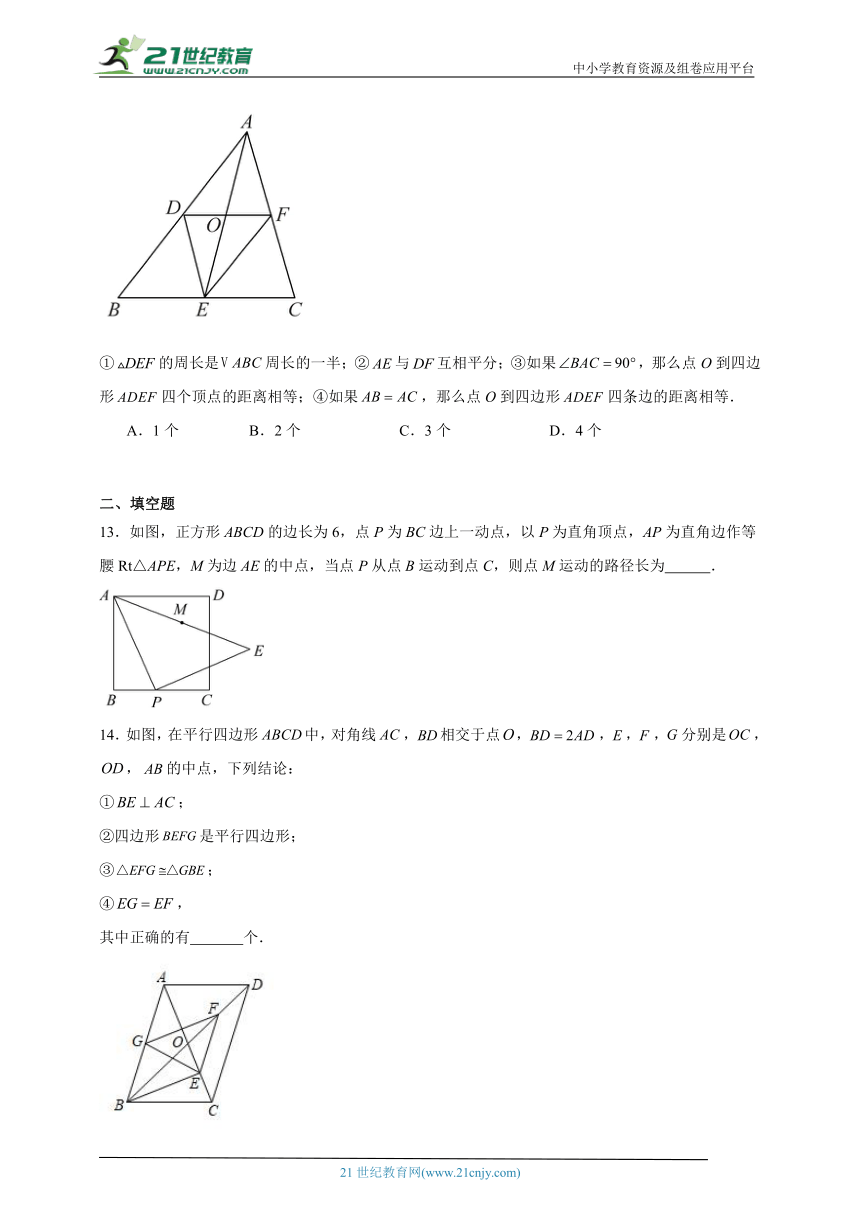
①的周长是周长的一半；②与互相平分；③如果，那么点O到四边形四个顶点的距离相等；④如果，那么点O到四边形四条边的距离相等．
A．1个 B．2个 C．3个 D．4个
二、填空题
13．如图，正方形ABCD的边长为6，点P为BC边上一动点，以P为直角顶点，AP为直角边作等腰Rt△APE，M为边AE的中点，当点P从点B运动到点C，则点M运动的路径长为 ．
14．如图，在平行四边形中，对角线，相交于点，，，，分别是，，的中点，下列结论：
①；
②四边形是平行四边形；
③；
④，
其中正确的有 个．
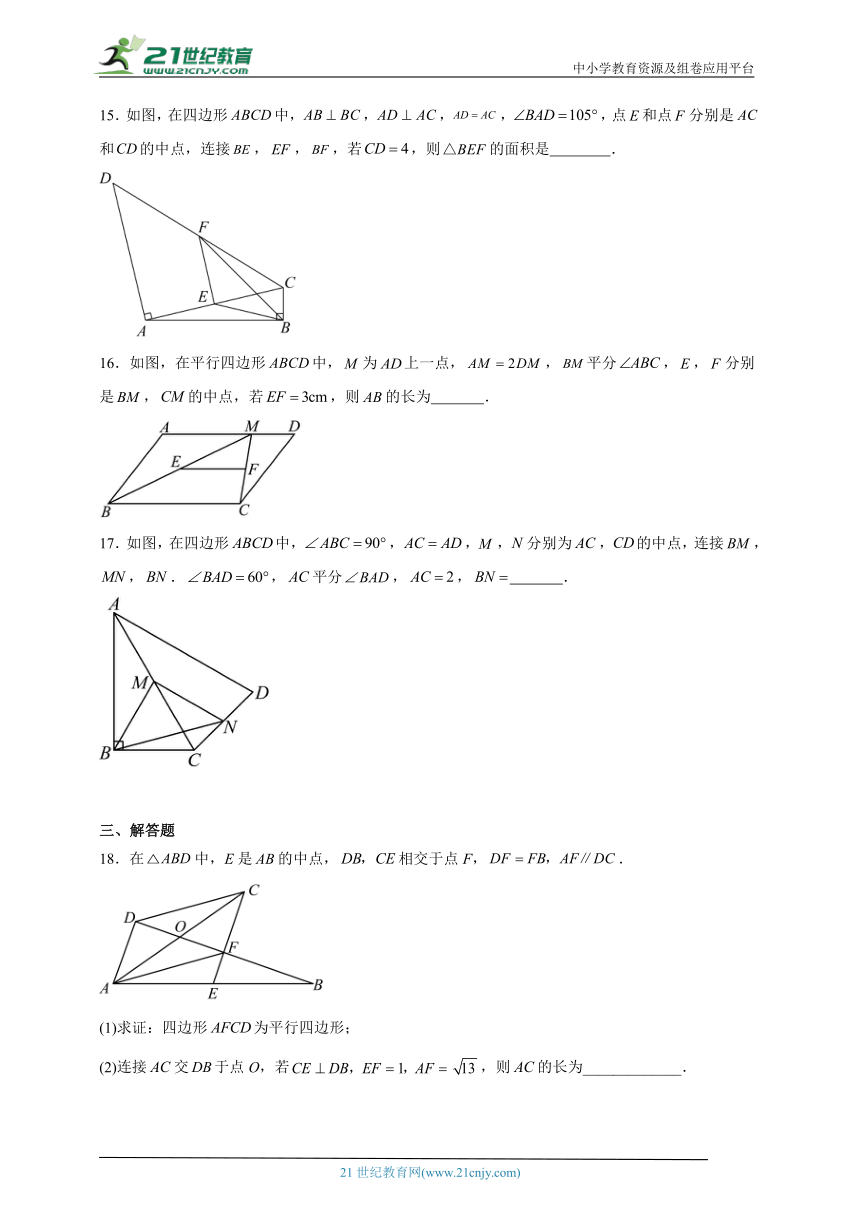
15．如图，在四边形中，，，，，点和点分别是和的中点，连接，，，若，则的面积是 ．
16．如图，在平行四边形中，为上一点，，平分，，分别是，的中点，若，则的长为 ．
17．如图，在四边形中，，，，分别为，的中点，连接，，．，平分，， ．
三、解答题
18．在中，E是的中点，相交于点F，．
(1)求证：四边形为平行四边形；
(2)连接交于点O，若，则的长为_____________．
19．在探索平面图形的性质时，往往需通过剪拼的方式帮助我们寻找解题思路．
（1）【知识回顾】
在证明三角形中位线定理时，就采用了如图①的剪拼方式，将三角形转化为平行四边形使问题得以解决，请写出已知，求证，并证明三角形中位线定理．
（2）【数学发现】
如图②，在梯形中，，是腰的中点，请你沿着将上图的梯形剪开，并重新拼成一个完整的三角形．
如图③，在梯形中，，、分别是两腰、的中点，我们把叫做梯形的中位线．请类比三角形的中位线的性质，猜想和、有怎样的位置和数量关系？
【证明猜想】
（3）证明（2）的结论，并在“，”的条件下，求的长．
20．已知在中，，为中点，为边的中线且，连接、．

(1)求证：；
(2)若，求的周长．
21．如图，在中，，，动点在的延长线上，是以为斜边的直角三角形，是的中点，连接，，且．
(1)证明：、、三点共线；
(2)连接．
①试判断线段与的数量关系，并给出证明；
②当，且线段取到最小值时，求的长度．
22．如图，在四边形中，E，F分别是，的中点，G，H分别是对角线，的中点，依次连接E，G，F，H，连接，．

(1)求证：四边形是平行四边形；
(2)当时，与有怎样的位置关系？请说明理由；
23．如图，在中，∠A＝60°，，垂足为F，点D、E分别为BC、AC上的点，连接BE，交CF于点M，连接DE、DF、EF．
(1)如图①，当BE⊥AC时：
①若CM＝4，FM＝2，求BE的长；．
②若AB＝AC，D为EC边上的中点，求证：△DEF时是等边三角形；．
(2)如图②，若AB≠AC，DB＝DF，DC＝DE，试猜想△DEF是不是等边三角形？如果是，请加以证明；如果不是，请说明理由．
24．如图，四边形ABCD是正方形，△ECF为等腰直角三角形，∠ECF＝90°，点E在BC上，点F在CD上，P为EF中点，连接AF，G为AF中点，连接PG，DG，将Rt△ECF绕点C顺时针旋转，旋转角为α（0°≤α≤360°）．
(1)如图1，当α＝0°时，DG与PG的关系为　　；
(2)如图2，当α＝90°时
①求证：△AGD≌△FGM；
②（1）中的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由．
《9.5三角形的中位线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C B B A C D C A D
题号 11 12
答案 B D
1．C
【分析】本题考查的是平行四边形的性质及三角形的中位线的性质．根据平行四边形的性质证明点为的中点，而点是边的中点，可证为的中位线，利用中位线定理解题即可．
【详解】解：由平行四边形的性质可知，
而为的中点，即，
为的中位线，，
，
．
故选：C．
2．C
【分析】延长至，使得，连接，构造等边三角形，根据题意可得是的中位线，即可求解．
【详解】解：如图，延长至，使得，连接，
，
,
又，
是等边三角形，
，
是边的中点，是边上一点，平分的周长，
，，
，
，
，
即，
是的中位线，，
．
故选C．
【点睛】本题考查了三角形中位线的性质与判定，等边三角形的性质，三角形中线的定义，构造等边三角形是解题的关键．
3．B
【分析】根据作图过程可得AM平分∠BAC，GH是边AB的垂直平分线，由等腰三角形三线合一，得AM是边BC上的中线，可得MN是△ABC的中位线，进而可得MN的长．
【详解】解：根据作图过程可知：AM平分∠BAC，GH是边AB的垂直平分线，
∵AB＝AC＝6，AM平分∠BAC，
∴AM是边BC上的中线，
∴BM＝CM，
∵GH是边AB的垂直平分线，
∴AN＝BN，
∴MN是△ABC的中位线，
∴MNAC＝3．
故选：B．
【点睛】此题考查了作图﹣复杂作图，角平分线的性质，线段垂直平分线的性质，等腰三角形的性质，熟知角平分线的作法是解题的关键．
4．B
【分析】如图，作GH⊥AD，BR⊥AD，，，利用角平分线和中位线的性质求得的长度，根据垂线段最短，即可求解．
【详解】解：如图，作GH⊥AD，BR⊥AD，GP⊥A＇F，A＇Q⊥AD，
∵∠BAD=45°，AB=10
∴为等腰直角三角形，
由题意可得，垂直平分，，
∴，
∴，
在中，，当、两点重合时，
即的最小值为
故选：B．
【点睛】此题考查了轴对称的性质，角平分线的性质，等腰直角三角形的性质，中位线的性质，垂线段最短，解题的关键是作出合适的辅助线，灵活运用相关性质进行求解．
5．A
【分析】根据三角形的中位线平行于第三边，并且等于第三边的一半，可得出△ABC的周长=2△DEF的周长．
【详解】∵D，E，F分别为各边的中点，
∴DE、EF、DF是△ABC的中位线，
∴DE=BC=3，EF=AB=2，DF=AC=4，
∴△DEF的周长=3+2+4=9．
故选：A．
【点睛】本题考查了三角形中位线定理．解题的关键是根据中位线定理得出边之间的数量关系．
6．C
【分析】取CD中点H，连接AH，BH，根据矩形的性质题意得出四边形AECH是平行四边形，可知，然后根据三角形中位线的性质得，得出点P在AH上，然后判断BP的最小值，再求出值即可.
【详解】如图，取CD中点H，连接AH，BH，设AH与DE的交点为O，
∵四边形ABCD是矩形，
∴AB＝CD＝8，AD＝BC＝4，，
∵点E是AB中点，点H是CD中点，
∴CH＝AE＝DH＝BE＝4，
∴四边形AECH是平行四边形，
∴，
∵点P是DF的中点，点H是CD的中点，
∴PH是△CDF的中位线，
∴，
∴点P在AH上，
∴当BP⊥AH时，此时点P与H重合，BP有最小值，
∵AD＝DH＝CH＝BC＝4，
∴∠DHA＝∠DAH＝∠CBH＝∠CHB＝45°，，
∴∠AHB＝90°，
∴BP的最小值为.
故选：C．
【点睛】本题主要考查了矩形的性质，平行四边形的判定，中位线的性质和定义等，确定点P的位置是解题的关键．
7．D
【分析】取AC的中点M，连接EM设由中位线性质可得再根据，可得出从而得到FC的长，即可得到的结果．
【详解】解：如图所示：取AC的中点M，连接EM，DM ，设
∵点是中点，
∴EM是的中位线，
四边形是菱形，
，∠AMD=90°，
，
∴DM=，
∴AM=
故选：D．
【点睛】本题主要考查了菱形的性质和中位线的性质，熟练掌握这些性质是解此题的关键．
8．C
【分析】本题考查平行四边形的性质、三角形的中位线定理、等边三角形的判定和性质、直角三角形30度角性质、垂线段最短等知识，解题的关键是学会添加常用辅助线，本题的突破点是证明，属于中考选择题中的压轴题．如图，取的中点M，连接，作于N．首先证明，求出，利用三角形中位线定理，可知，求出的最大值以及最小值即可解决问题．
【详解】解：如图，取的中点M，连接，作于N．

∵四边形是平行四边形，，
∴，
∵，
∴是等边三角形，
∴，
∴，
∴，
∴，
在中，
∵，
∴，
∵，
∴，
易知的最大值为的长，最小值为的长，
∴的最大值为，最小值为，
∴的最大值为，最小值为，
∴的最大值与最小值的差为．
故选：C．
9．A
【分析】由 ABCD中，∠ADC＝60°，易得ABE是等边三角形，又由AB＝BC，证得①∠CAD＝30°；继而证得AC⊥AB，得②S ABCD＝AB AC；可得OE是三角形的中位线，证得④OE＝BC
【详解】解：∵四边形ABCD是平行四边形，
∴∠ABC＝∠ADC＝60°，∠BAD＝120°，
∵AE平分∠BAD，
∴∠BAE＝∠EAD＝60°
∴ABE是等边三角形，
∴AE＝AB＝BE，
∵AB＝BC，
∴AE＝BC，
∴∠BAC＝90°，
∴∠CAD＝30°，故①错误；
∵AC⊥AB，
∴S ABCD＝AB AC，故②错误；
∵AB＝BC，OB＝BD，
∵BD＞BC，
∴AB≠OB，故③错误；
∵∠CAD＝30°，∠AEB＝60°，ADBC，
∴∠EAC＝∠ACE＝30°，
∴AE＝CE，
∴BE＝CE，
∵OA＝OC，
∴OE＝AB＝BC，故④正确；
故选：A．
【点睛】此题考查了平行四边形的性质、三角形中位线的性质以及等边三角形的判定与性质．注意证得ABE是等边三角形，OE是ABC的中位线是关键．
10．D
【分析】连接AC、BD交于点O，连接GO、HO，可得GO、HO分别是△ACE、△BDF的中位线，从而求出GO，HO的长，在通过证明△GOH是直角三角形，利用勾股定理求出GH的长．
【详解】解：连接AC、BD交于点O，连接GO、HO，如图所示，
∵点E、F分别是AB、BC的中点．
∴AE=AB=2，BF=BC＝2．
∵点O是正方形ABCD对角线的交点．
∴点O是AC、BD的中点．
∵点G是EC的中点．
∴GO是△ACE的中位线．
∴GO=AE=1，且GO∥AB．
同理，HO=1，且HO∥BC．
∵∠ABC=90°．
∴AB⊥BC．
∴GO⊥HO．
∴∠GOH=90°．
在Rt△GOH中，
GH=．
故选：D．
【点睛】本题考查了正方形的性质与三角形的中位线性质定理，通过作辅助线把GH归纳到直角三角形中是解题的关键．
11．B
【分析】根据全等三角形的性质可得AE=CE，DE=EF，再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形，然后利用等腰三角形三线合一的性质求出∠ADC=90°，再利用有一个角是直角的平行四边形是矩形解答．
【详解】解：△ADE≌△CFE，
∴AE=CE，DE=EF，
∴四边形ADCF是平行四边形，
∵AC=BC，点D是边AB的中点，
∴∠ADC=90°，
∴四边形ADCF是矩形．
故选：B．
【点睛】本题考查了矩形、菱形、正方形的判定，全等三角形的性质，等腰三角形的性质，熟练掌握矩形的判定定理是解题的关键．
12．D
【分析】①根据中位线的性质，即可判断；②根据中位线的性质、一组对边平行且相等的四边形是平行四边形、平行四边形的对角线互相平分，即可判断；③根据矩形的判定和性质，即可判断；④根据菱形的判定和性质，即可判断．
【详解】解：①∵点D、E、F分别为边、、的中点，
∴DE、EF、DF是的中位线，
∴，
∴，
即的周长是周长的一半，
故①正确，符合题意；
②∵点D、E、F分别为边、、的中点，
∴是的中位线，
∴，
∴，
∴四边形ADEF是平行四边形，
∴与互相平分，
故②正确，符合题意；
③由②得四边形ADEF是平行四边形，
当时，如图1，
∴四边形ADEF是矩形，
∴，
∴，
∴点O到四边形四个顶点的距离相等，
故③正确，符合题意；
④由①得，
当时，如图2，
∴，
由②得四边形ADEF是平行四边形，
∴四边形ADEF是菱形，
∴，
∴，
∴，
∴点O到四边形四条边的距离相等，
故④正确，符合题意．
故选D．
【点睛】本题主要考查了中位线的性质、平行四边形的判定和性质、矩形的判定和性质、菱形的判定和性质．
13．
【分析】连接AC，BD相交于点O，连接EC，过点E作ET⊥BC交BC的延长线于T．根据正方形的性质，全等三角形的判定定理和性质可确定AB=PT，PB=ET，根据线段的和差关系和等边对等角确定∠TCE=45°，根据平行线的判定定理可确定，根据正方形的性质和三角形的中位线定理可确定，进而可确定点M的运动轨迹是OD，最后根据正方形的性质和勾股定理即可求出OD的长度．
【详解】解：如下图所示，连接AC，BD相交于点O，连接EC，过点E作ET⊥BC交BC的延长线于T．
∵△APE是等腰直角三角形，
．
∴∠APB+∠TPE=90°．
∵四边形ABCD是正方形，ET⊥BC，
∴∠ABP=90°，∠PTE=90°．
∴∠ABP=∠PTE，∠BAP+∠APB=90°．
∴∠BAP=∠TPE．
．
．
∵四边形ABCD是正方形，
．
．
∴BC-PC=PT-BC，即PB=CT．
．
∴∠TEC=∠TCE=45°．
∵正方形ABCD中，AC，BD相交于点O，
∴O是AC的中点，∠DBC=45°．
∴∠DBC=∠TCE．
．
∵M是AE的中点，
∴OM是△ACE的中位线．
∴．
∴点M在直线OD上．
∵点P在BC边上移动，
∴点M的运动轨迹是OD．
∵正方形ABCD的边长是6，且AC，BD相交于点O，
∴AB=6，AD=6，O是BD的中点．
∴．
∴．
故答案为：．
【点睛】本题考查正方形的性质，全等三角形的判定定理和性质，三角形中位线定理，平行线的判定定理，勾股定理，正确确定点M的运动轨迹是解题关键．
14．
【分析】由平行四边形的性质可得AB=CD，AD=BC，BO=DO=BD，AO=CO，ABCD，即可得BO=DO=AD=BC，由等腰三角形的性质可判断①，由中位线定理和直角三角形的性质可判断②④，由平行四边形的性质可判断③，即可求解．
【详解】解：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，BO=DO=BD，AO=CO，ABCD，
∵BD=2AD，
∴BO=DO=AD=BC，且点E是OC中点，
∴BE⊥AC，
∴①正确；
∵E、F、分别是OC、OD中点，
∴EFDC，CD=2EF，
∵G是AB中点，BE⊥AC，
∴AB=2BG=2GE，且CD=AB，CDAB，
∴BG=EF=GE，EFCDAB，
∴四边形BGFE是平行四边形，
∴②④正确；
∵四边形BGFE是平行四边形，
∴BG=EF，GF=BE，且GE=GE，
∴△BGE≌△FEG（SSS），
∴③正确．
故答案为：4．
【点睛】本题考查了平行四边形的判定和性质，全等三角形的判定和性质，直角三角形的性质，等腰三角形的性质，熟练运用这些性质进行推理是本题的关键．
15．
【分析】先根据三角形的中位线定理与直角三角形的性质，可得，然后过点作于，根据等腰三角形性质与直角三角形性质可得和的长度，再根据三角形面积公式求解即可．
【详解】解：如图，过点作于．
，，，
，
点和点分别是和的中点，
，，
，
，，
，
，
，，
，
，
，
，
，
，
，，
，
．
故答案为：．
【点睛】此题考查了三角形中位线定理、直角三角形的性质、等腰三角形的判定与性质与三角形面积公式等知识，熟练掌握相关的定理、性质与公式是解题的关键．
16．
【分析】本题考查了平行四边形的性质、三角形中位线的性质、角平分线的性质．首先根据三角形中位线的性质可知，根据平行四边形的性质可知，根据角平分线的性质和平行四边形的性质可证，根据等角对等边可得，从而可得．
【详解】解：，分别是，的中点，，
，
平分，
，
四边形是平行四边形，
，，
，
，
，
，
，
，
．
故答案为： ．
17．
【分析】本题考查了三角形中位线定理、直角三角形斜边中线定理、勾股定理等知识，根据三角形中位线定理得，根据直角三角形斜边中线定理得，由此即可证明．再证明，根据即可解决问题．
【详解】解：在中，、分别是、的中点，
，，
在中，是中点，
，
，
，
，平分，
，
，
，
，
，
，
，，
．
故答案为：．
18．(1)见解析
(2)
【分析】本题考查了平行四边形的判定与性质、三角形的中位线定理、勾股定理等知识点，掌握相关结论是解题关键．
（1）由题意得是的中位线，推出，结合即可求证；
（2）由题意得，，，故可求出，，结合即可求解；
【详解】（1）证明：∵E是的中点，
∴是的中位线，
∴，
即：，
∵，
∴四边形为平行四边形
（2）解：∵是的中位线，
∴，
∵四边形为平行四边形，
∴，，
∴，
∴，
∴，
∴
故答案为：
19．（1）见解析；（2）画图见解析，猜想：，；（3）证明见解析，6；
【分析】本题主要考查了三角形中位线定理，平行四边形的性质与判定，全等三角形的性质与判定：
（1）根据三角形中位线定理的内容写出对应的已知，求证和证明过程即可；
（2）延长交延长线于M，证明可得到所要的三角形；根据梯形性质和三角形的中位线进行猜想即可得出结论；
（3）如图③，连接并延长，交延长线于点，证明得到，，在中，利用三角形的中位线可证得，，进而可证得结论；再根据结论求出的长即可．
【详解】解：（1）已知：在中，分别是的中点，
求证：：
证明：如图所示，过点C作交延长线与F，
∵分别是的中点，
∴，
∵，
∴，
∴，
∴，
∴，
∴四边形是平行四边形，
∴，
∴；
（2）如图所示，延长交延长线于M，则把延剪开后放置到的位置，即为所求；
猜想：，；
（3）连接并延长，交延长线于点，
，
．
是的中点，
．
，
．
，．
点是的中点，又点是的中点，
是的中位线，
，．
．
，，
．
，．
∵，，
∴。
20．(1)证明见解析
(2)
【分析】（1）由三角形中线性质得到，再由等腰三角形性质、三角形外角的性质及等腰三角形性质得，可得结论；
（2）先由中位线的判定与性质得到，再由是等边三角形，确定含的直角三角形，结合含的直角三角形及勾股定理求出三边的边长，即可得结论．
【详解】（1）证明：为边的中线且，
，
，
，，
，
，
，
；
（2）解：为中点，为边的中线，
为的中位线，
，
，
是等边三角形，
，
，
，
，
，
，，
的周长．
【点睛】本题考查三角形的周长、等腰三角形判定与性质、等边三角形判定与性质、含的直角三角形性质、三角形的中线、中位线、勾股定理等知识，解题的关键是熟练掌握相关几何基础知识．
21．(1)见解析；
(2)①EC=OA，证明见解析；②．
【分析】（1）证明∠AFE+∠AFB=180°，可得结论；
（2）①结论：EC=AO．连接EO，OC，证明△EOC是等腰直角三角形，可得结论；
②如图2中，取AE的中点J，连接OJ．证明OJ∥EB，推出OF⊥OJ时，OF的值最小，此时四边形OFEJ是矩形，利用勾股定理求出OA，可得结论．
【详解】（1）证明：∵∠AEF=90°，AE=EF，
∴∠EAF=∠EFA=45°，
∵2∠CBF+∠EAF=135°，
∴∠CBF=45°，
∵∠C=90°，
∴∠CFB=90°-45°=45°，
∴∠CFB=∠AFE，
∵∠CFB+∠AFB=180°，
∴∠AFE+∠AFB=180°，
∴E、F、B共线．
（2）解：①结论：EC=OA．
理由：如图1中，连接EO，CO．
∵∠AEB=∠ACB=90°，OA=OB，
∴OE=OA=OB=OC，
∴∠OAC=∠OCA，∠OEB=∠OBE，
∵∠BOC=∠OAC+∠OCA=2∠OCA，∠AOE=∠OEB+∠OBE=2∠OBE，
∴∠BOC+∠AOE=2∠CAO+2∠OBE=2（∠OAC+∠OBE）=2∠CFB=90°，
∴∠EOC=90°，
∴△EOC是等腰直角三角形，
∴EC=EO=OA；
②如图2中，取AE的中点J，连接OJ．
∵AJ=EJ，AO=OB，
∴OJ∥EB，
∴OF⊥OJ时，OF的值最小，此时四边形OFEJ是矩形，
∴EF=AE=OJ=2，AJ=EJ=1，
∴，
∴EC=OA=．
【点睛】本题属于三角形综合题，考查了等腰直角三角形的性质和判定，勾股定理，三角形中位线定理，垂线段最短等知识，解题的关键是学会添加常用辅助线，构造等腰直角三角形解决问题．
22．(1)见详解
(2)，理由见详解
【分析】（1）因为E，F分别是，的中点，G，H分别是对角线，的中点，所以是的中位线，是的中位线，故，，，，即，，即可作答；
（2）因为E是的中点，H是的中点，所以是的中位线，则，，由（1）知，结合，得，又因为四边形是平行四边形，所以四边形是菱形，即可作答．
【详解】（1）证明：因为E，F分别是，的中点，G，H分别是对角线，的中点，所以是的中位线，
所以是的中位线，是的中位线，
故，，，，
那么，，
所以四边形是平行四边形；
（2）解：，理由如下：
因为E是的中点，H是的中点，
所以是的中位线，
则，，
因为，且结合由（1）知，
所以，
因为四边形是平行四边形，
因为
因为四边形是平行四边形，
故
【点睛】本题考查了中位线的性质、平行四边形的判定与性质，以及菱形的判定等知识内容；中位线的性质：平行于三角形的第三边，且等于第三边的一半，正确掌握相关性质内容是解题的关键．
23．(1)①；②见解析
(2)是，见解析
【分析】（1）①先由，，，得出即可得出，同理可得出，即可得出；②由，AB＝AC，可得出是等边三角形，即可得出AB＝AC＝BC，再根据中位线的性质，得出：EF＝ED＝DF，即可得证；
（2）由题干条件可推导出：，进而得出∠DCF＝∠DFC，故而DF＝DC，也就是DF＝DE，即可证明是等边三角形．
【详解】（1）①解：∵，，，
∴，
∴，，
∴．
②证明：∵，AB＝AC，
∴是等边三角形，
∴AB＝AC＝BC．
∵，垂足为E，，垂足为F，
∴E、F分别是AC、AB边的中点．．
又∵点D是BC的中点，
∴EF、DE、DF是的中位线，
∴，，．
∴EF＝ED＝DF，
∴是等边三角形
（2）解：是等边三角形．证明如下：
∵，
∴．
∵DB＝DF，DC＝DE，
∴，∠DEC＝∠ACB，
∴，
∴．
∵，
∴，．
∵∠DBF＝∠DFB，
∴∠DCF＝∠DFC，
∴DF＝DC，
∴DF＝DE，
∴是等边三角形．
【点睛】本题考查的是等边三角形的判定和性质，中位线的判定和性质，30°直角三角形的性质，掌握在以上知识点是解题的关键．
24．(1)且
(2)①见解析；②成立，理由见解析
【分析】（1）先判断出，得出，，再用直角三角形斜边的中线等于斜边的一半和三角形中位线定理、三角形外角和定理，即可得出结论；
（2）①先判断出，再判断出，即可得出结论；
②由①知，，得，得出，根据题（1），得出，得，得．又根据点是的中点，是的中位线，等量代换得．根据得，且，推出，又根据，同旁内角互补，得，即．
【详解】（1）解：∵四边形ABCD是正方形
∴，
∵为等腰直角三角形
∴
∴CE＝CF，
∴
∴，
∵点是的中点
∴
∴
∵为中点，为中点
∴是的中位线
∴，
∴，
又∵在中
∴且
∴
∵
∴
∴
∴
∴
故且．
故答案是：DG=PG且DG⊥GP；
（2）①证明：∵四边形是正方形，
∴
∵点是的中点
∴
∴在和中
∴
解：②（1）中的结论且成立
证明：由①知，
∴，
∴
∴
∵
∴
又∵，
∴
∴，
∵点是的中点
∴
又∵为中点，为中点
∴是的中位线
∴，
∴
又∵
∴
∴
∴
又∵
∴
∴
∴
故且．
【点睛】此题是四边形综合题，主要考查了正方形的性质，全等三角形的判定和性质，等腰直角三角形的性质，三角形的中位线定理，解题的关键是全等三角形性质，三角形中位线定理，等量代换的转换运用．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)