第七章数据的收集、整理、描述同步练习(含解析)
文档属性
| 名称 | 第七章数据的收集、整理、描述同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 570.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 18:50:24 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章数据的收集、整理、描述
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为了解某校1500名学生的体重情况,从中抽取了100名学生的体重,就这个问题来说,下面说法正确的是( )
A.每个学生是个体 B.1500名学生是总体
C.1500名学生的体重是总体 D.100名学生是所抽取的一个样本
2.为了了解我校八年级的1200名学生的数学期中成绩,随机抽取80名学生的数学成绩进行分析,则下列说法错误的是( )
A.总体是我校八年级的1200名学生的数学期中成绩的全体
B.其中80名学生是总体的一个样本
C.样本容量是80
D.个体是我校八年级学生中每名学生数学期中成绩
3.2009年5月31日世界无烟日的口号是“戒烟一小时,健康亿人行”.小华学习小组为了解本地区大约有多少成年人吸烟,随机调查了100个成年人,结果其中有15个成年人吸烟.对于这个关于数据收集与描述的问题,下列说法正确的是( ).
A.调查的方式是普查 B.本地区只有85个成年人不吸烟
C.样本是15个吸烟的成年人 D.本地区约有的成年人吸烟
4.每年的3月21日是世界睡眠日,良好的睡眠状态是保持身体健康的重要基础,为了解某学校800名初一学生的睡眠时间,从21个班级中随机抽取50名学生进行调查,下列说法不正确的是( )
A.总体是该校800名初一学生的睡眠时间的全体
B.个体是每名初一学生的睡眠时间
C.样本是从中抽取的50名学生
D.样本容量是50
5.下列调查中,适合普查的是( )
A.调查某班级40名学生的身高情况
B.调查一批草莓的口感
C.调查盐城市人民对某政策的支持程度
D.了解全市学生桌椅的质量情况
6.2024年市有万名学生参加中考,为了了解这些考生的数学成绩,从中抽取200名考生的数学成绩进行统计分析,在这个问题中,下列说法:
①这万名考生的数学成绩是总体;
②每个考生是个体;
③200名考生是总体的一个样本;
④样本容量是200,
其中说法正确的有( )
A.4个 B.3个 C.2个 D.1个
7.为了解某校九年级400名学生的体重情况,从中随机抽取50名学生的体重进行分析,在这项调查中,样本是( )
A.400名学生 B.被抽取的50名学生
C.400名学生的体重 D.被抽取的50名学生的体重
8.某市教育局对七年级学生进行体质监测,共收集了名学生的体重数据,并绘制成频数分布直方图.若从左往右数每个小长方形的面积之比为,则其中第三组的频数为( )
A. B. C. D.
9.神舟十九号载人飞船在酒泉卫星发射中心点火发射,神舟十九号航天员乘组顺利进驻中国空间站,关于此次发射任务,不适合做全面调查的是( )
A.调查神舟十九号载人飞船的零部件是否符合标准
B.调查三位宇航员的身体状况
C.调查宇航员的太空服是否符合安全标准
D.调查神舟十九号载人飞船发射时的收视率
10.下列调查方式中适合的是( )
A.要了解一批节能灯的使用寿命,采用普查方式
B.调查你所在班级同学的身高,采用抽样调查方式
C.环保部门调查沱江某段水域的水质情况,采用抽样调查方式
D.调查全市中学生每天的就寝时间,采用普查方式
11.有60个数据,其中最大值为40,最小值为20.若取组距为5,则这组数据应该分成( )
A.3组 B.4组 C.5组 D.6组
12.养殖户老杨为了估计自己鱼塘1斤以上的鱼有多少条,老杨先从鱼塘里捞出了100条1斤以上的鱼做上标记,然后放回鱼塘里.经过一段时间,带有标记的鱼完全混合于鱼群后,老杨又从鱼塘捞出200条1斤以上的鱼,其中20条有标记,那么估计鱼塘里有1斤以上的鱼( )
A.1000条 B.2000条 C.3000条 D.4000条
二、填空题
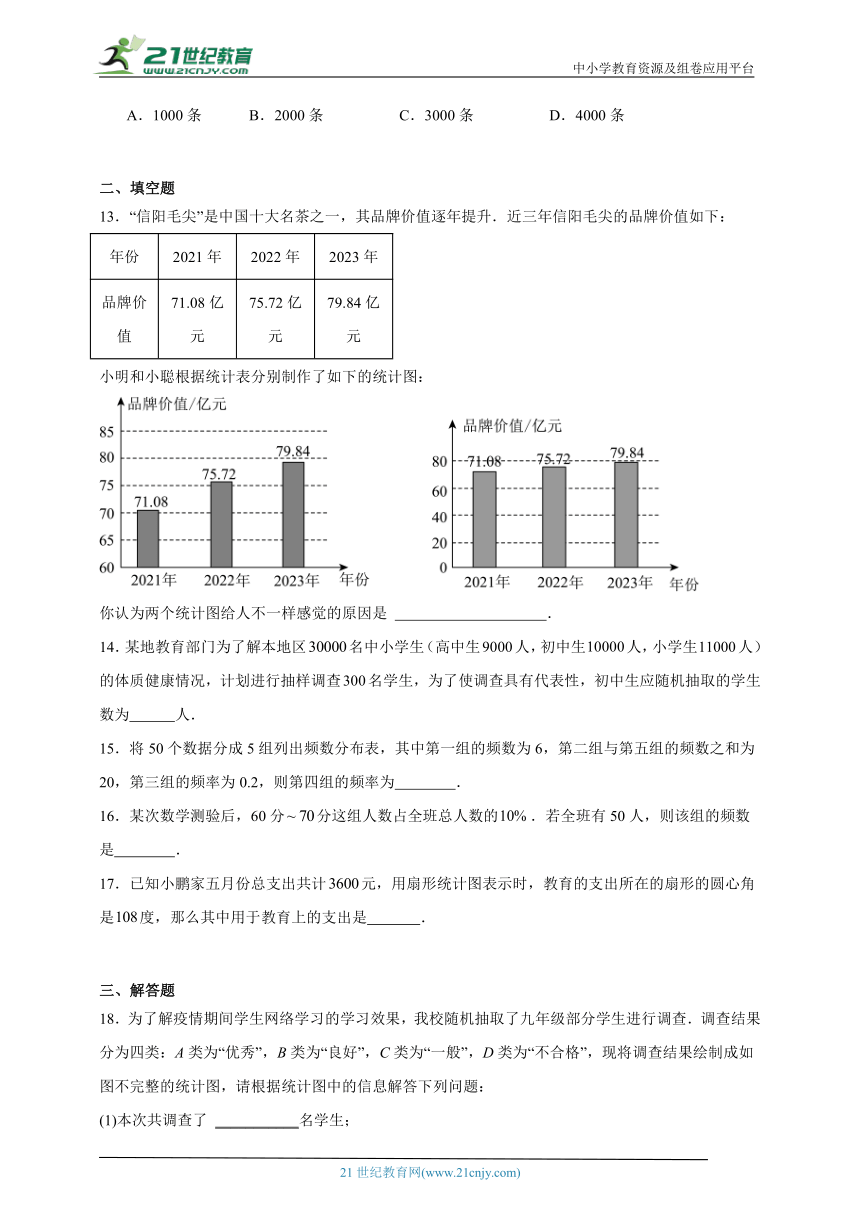
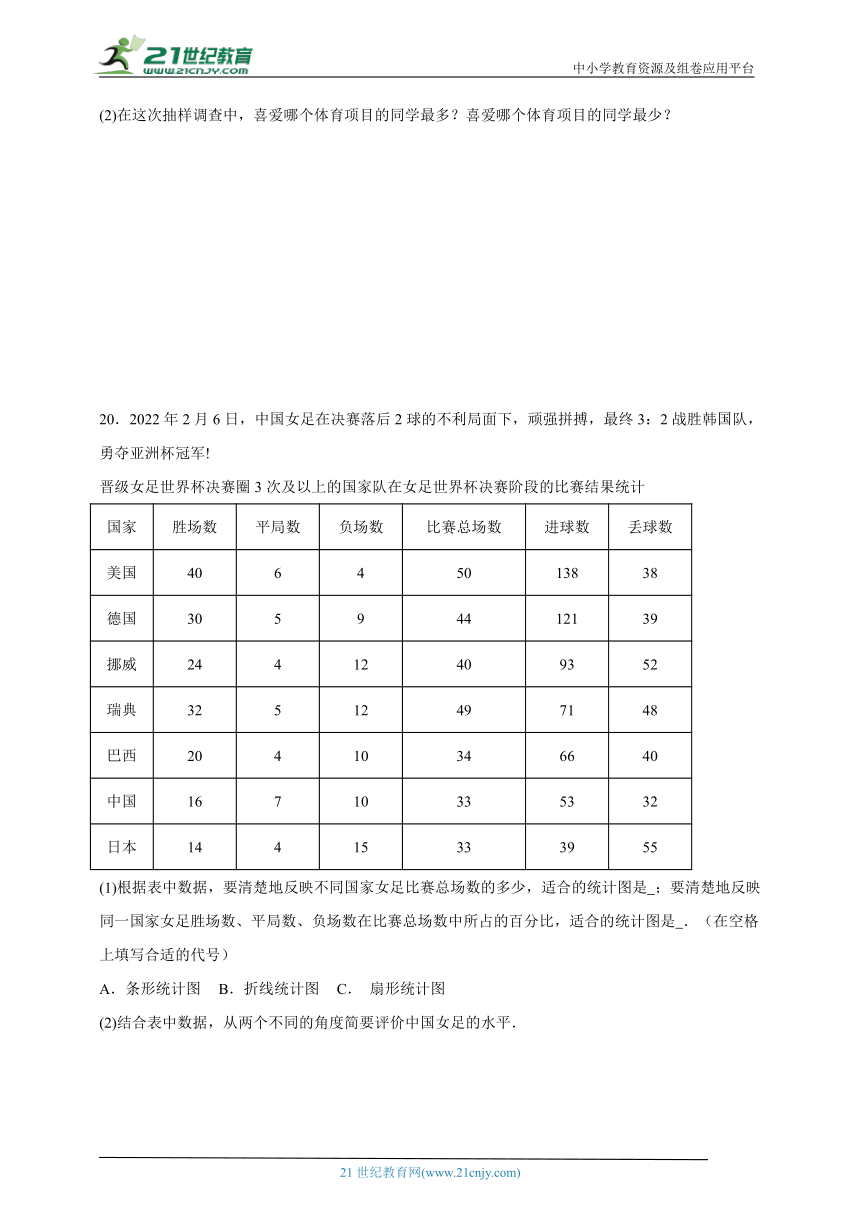
13.“信阳毛尖”是中国十大名茶之一,其品牌价值逐年提升.近三年信阳毛尖的品牌价值如下:
年份 2021年 2022年 2023年
品牌价值 71.08亿元 75.72亿元 79.84亿元
小明和小聪根据统计表分别制作了如下的统计图:
你认为两个统计图给人不一样感觉的原因是 .
14.某地教育部门为了解本地区名中小学生(高中生人,初中生人,小学生人)的体质健康情况,计划进行抽样调查名学生,为了使调查具有代表性,初中生应随机抽取的学生数为 人.
15.将50个数据分成5组列出频数分布表,其中第一组的频数为6,第二组与第五组的频数之和为20,第三组的频率为0.2,则第四组的频率为 .
16.某次数学测验后,60分分这组人数占全班总人数的.若全班有50人,则该组的频数是 .
17.已知小鹏家五月份总支出共计元,用扇形统计图表示时,教育的支出所在的扇形的圆心角是度,那么其中用于教育上的支出是 .
三、解答题
18.为了解疫情期间学生网络学习的学习效果,我校随机抽取了九年级部分学生进行调查.调查结果分为四类:A类为“优秀”,B类为“良好”,C类为“一般”,D类为“不合格”,现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
(1)本次共调查了 ___________名学生;
(2)补全条形统计图:D类所对应扇形的圆心角的大小为 ___________;
(3)若我校九年级学生共有1700名,根据以上抽样结果,估计我校九年级学生学习效果为“优秀”的学生约有多少名?
19.我市教育局倡导中小学开展艺体普及活动,某校学生会为了了解全校同学对各项目的喜爱情况,随机调查了200名同学(每位同学仅选一项最喜爱的项目),根据调查结果制作了频数分布表:
最喜爱的项目 频数(人数) 所占百分比
篮球 28%
排球 24 12%
乒乓球 48 24%
健美操
武术操 22 11%
跑步 20 10%
合计 200 100%
(1)请补全频数分布表;
(2)在这次抽样调查中,喜爱哪个体育项目的同学最多?喜爱哪个体育项目的同学最少?
20.2022年2月6日,中国女足在决赛落后2球的不利局面下,顽强拼搏,最终3:2战胜韩国队,勇夺亚洲杯冠军!
晋级女足世界杯决赛圈3次及以上的国家队在女足世界杯决赛阶段的比赛结果统计
国家 胜场数 平局数 负场数 比赛总场数 进球数 丢球数
美国 40 6 4 50 138 38
德国 30 5 9 44 121 39
挪威 24 4 12 40 93 52
瑞典 32 5 12 49 71 48
巴西 20 4 10 34 66 40
中国 16 7 10 33 53 32
日本 14 4 15 33 39 55
(1)根据表中数据,要清楚地反映不同国家女足比赛总场数的多少,适合的统计图是 ;要清楚地反映同一国家女足胜场数、平局数、负场数在比赛总场数中所占的百分比,适合的统计图是 .(在空格上填写合适的代号)
A.条形统计图 B.折线统计图 C. 扇形统计图
(2)结合表中数据,从两个不同的角度简要评价中国女足的水平.
21.在数学、外语、语文3门学科中,某校七年级开展了同学们最喜欢学习哪门学科的调查(七年级共有200人).
(1)调查的总体和个体是什么?
(2)在被调查的200名学生中,有40人最喜欢学语文,60人最喜欢学数学,80人最喜欢学外语,其余的人选择其他,求最喜欢学数学这门学科的学生占学生总数的百分比.
22.5月初,某校组织九年级学生测量身高,该校九年级共有5个班,小华同学根据各班学生人数绘制了以下两幅统计图.
(1)该校九年级学生总数为 .
(2)请补全条形统计图,扇形统计图中“2班”所在扇形的圆心角的度数为 .
(3)九(2)班学生先一步测量身高,统计发现身高在的有30人,若该校九年级身高在的学生占比和九(2)班的占比情况相当,请估计九年级学生身高在的人数.
23.2022年是中国共产主义青年团建团100周年,某校团委组织全校二十四个班级同学开展主题为“成团百年,勇当先锋”的团史知识学习活动,为了解这二十四个班级的同学团史知识的学习情况,团里的小明、小亮分别设计了如下方案.
小明:调查出自己所在班级的每个同学的团史知识学习情况,以此推算出这二十四个班级同学的团史知识学习情况.
小亮:在这二十四个班级中,抽取学号为5的整数倍的72名同学,调查他们的团史知识学习情况,从而估计这二十四个班级同学的团史知识学习情况.
这两种方案哪一种比较好?请说明理由.
24.为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 文学鉴赏 国际象棋 音乐舞蹈 书法 其他
所占百分比
根据统计图表的信息,解答下列问题:
(1)本次抽样调查的学生有 人;
(2)统计表中的 , ;
(3)选择“国际象棋”的学生有 人;
(4)若该校共有名学生,试估计全校选择“音乐舞蹈”社团的学生有 人.
《第七章数据的收集、整理、描述》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D C A C D A D C
题号 11 12
答案 C A
1.C
【分析】总体是指考查的全体对象,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分考察对象.
【详解】A.、每个学生的体重是个体,错误;
B、1500名学生的体重是总体,错误;
C、1500名学生的体重是总体,正确;
D、100名学生的体重是所抽取的一个样本,错误.
故选:C..
【点睛】正确理解总体、个体、样本的概念是解决本题的关键.
2.B
【分析】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】解:A.总体是我校八年级的1200名学生的数学期中成绩的全体,说法正确,故本选项不符合题意;
B.其中80名学生的数学期中成绩是总体的一个样本,原说法错误,故本选项符合题意;
C.样本容量是80,说法正确,故本选项不符合题意;
D.个体是我校八年级学生中每名学生数学期中成绩,说法正确,故本选项不符合题意.
故选:B.
3.D
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:根据题意,随机调查100个成年人,是属于抽样调查,
这100个人中85人不吸烟不代表本地区只有85个成年人不吸烟,
样本是100个成年人,所以本地区约有的成年人吸烟是正确的.
故选:D.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.C
【分析】根据总体、个体、样本、样本容量之间的关系进行判断即可.
【详解】解:A、总体是该校800名初一学生的睡眠时间的全体,故选项正确,不符合题意;
B、个体是每名初一学生的睡眠时间,故选项正确,不符合题意;
C、从21个班级中随机抽取50名学生的睡眠时间是样本,故选项错误,符合题意;
D、样本容量是50,故选项正确,不符合题意;
故选:C.
【点睛】本题考查总体、个体、样本、样本容量,理解总体、样本、样本容量的意义是正确解答的关键.
5.A
【分析】根据适合普查的分式一般有一下几种:范围较小,易容掌控,不具有破坏性,可操作性强;即可进行判断.
【详解】解:A. 调查某班级40名学生的身高情况,应采用普查,此选项符合题意;
B. 调查一批草莓的口感,应选择抽样调查,此选项不合题意;
C. 调查盐城市人民对某政策的支持程度,应选择抽样调查,此选项不合题意;
D. 了解全市学生桌椅的质量情况,应选择抽样调查,此选项不合题意;
故选:A.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
6.C
【分析】本题考查总体、个体、样本、样本容量,理解总体、样本、样本容量的意义是正确解答的关键.
根据考查的对象是万名学生的中考数学成绩,利用总体、个体、样本、样本容量之间的关系进行判断即可.
【详解】解:这万名考生的数学成绩是总体,故①说法正确;
每个考生的数学成绩是个体,故②说法错误;
200名考生的数学成绩是总体的一个样本,故③说法错误;
样本容量是200故④说法正确;
所以,说法正确的有2个,
故选:C.
7.D
【分析】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
根据总体、个体、样本、样本容量的定义判断即可.
【详解】解:为了解某校九年级400名学生的体重情况,从中随机抽取50名学生的体重进行分析,在这项调查中,样本是被抽取的50名学生的体重.
故选:.
8.A
【分析】本题考查了频数分布直方图的性质,理解频数分布直方图的意义,掌握频率是解答本题的关键.
求出第三组的频数占被调查人数的百分比,再根据频率进行计算即可.
【详解】解:第三组的频数为,
故选:A.
9.D
【分析】本题考查的是全面调查和抽样调查,根据全面调查和抽样调查的概念判断即可.通过普查可以直接得到较为全面、可靠的信息,但花费的时间较长,耗费大,且一些调查项目并不适合普查.其一,调查者能力有限,不能进行普查.其二,调查过程带有破坏性.其三,有些被调查的对象无法进行普查.
【详解】解:A、查神舟十九号载人飞船的零部件是否符合标准,适合做全面调查,不符合题意;
B、调调查三位宇航员的身体状况,适合做全面调查,不符合题意;
C、调查宇航员的太空服是否符合安全标准,适合做全面调查,不符合题意;
D、调查神舟十九号载人飞船发射时的收视率,不适合做全面调查,符合题意.
故选:D.
10.C
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,逐项进行判断即可.
【详解】解:A.要了解一批节能灯的使用寿命,采用抽样调查,故A不符合题意;
B.调查你所在班级的同学的身高,应该采用普查,故B不符合题意;
C.环保部门调查沱江某段水域的水质情况,应该采用抽样调查,故C符合题意;
D.调查全市中学生每天的就寝时间,应该采用抽样调查,故D不符合题意.
故选:C.
【点睛】本题主要考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
11.C
【解析】略
12.A
【分析】用先从鱼塘里捞出的100条1斤以上的鱼的数量除以所抽样本中1斤以上的鱼所占比例即可.
【详解】解:估计鱼塘里有1斤以上的鱼有100÷=1000(条),
故选:A.
【点睛】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
13.两个统计图纵轴的单位长度不相同,且第一个统计图的纵轴不都是从0开始的
【分析】本题考查了条形统计图,根据两个统计图的纵轴的区别求解即可.
【详解】解:由图可得,两个统计图给人不一样感觉的原因是:两个统计图纵轴的单位长度不相同,且第一个统计图的纵轴不都是从0开始的,
故答案为:两个统计图纵轴的单位长度不相同,且第一个统计图的纵轴不都是从0开始的.
14.
【分析】利用抽取的百分比乘初中生的总数即可得.
【详解】解:(人),
故答案为:.
【点睛】本题考查了抽样调查,解题的关键是得出抽取比例.
15.0.28
【分析】本题考查了频数(率)分布表先计算出第三组的频数为10,再计算出第四组的频数为14,然后根据频率的定义计算第四组的频率.
【详解】解:第三组的频数为,
所以第四组的频数为,
所以第四组的频率.
故答案为0.28.
16.5
【分析】本题考查求频数,利用总数乘以频率进行求解即可.
【详解】解:;
故答案为:5.
17.元
【分析】本题考查了扇形统计图.根据圆心角的度数得出教育的支出的占比,乘以,即可求解.
【详解】解:依题意,其中用于教育上的支出为(元),
故答案为:元.
18.(1)50
(2)
(3)510
【分析】(1)根据类的人数和所占的百分比求出抽查的总人数.
(2)用总人数减去其他类别的人数,求出类的人数,从而补全条形图;用乘以类所占百分比即可得出类所对应的扇形圆心角度数.
(3)用总人数乘以九年级学生学习效果为“优秀” 的学生人数所占的百分比即可.
【详解】(1)这次一共抽取的学生有:
(名),
故答案为:50.
(2)类的人数有:(名),补全统计图如下:
扇形统计图中类所对应的扇形圆心角大小为:,
故答案为:.
(3)(名),
答:估计我校九年级学生学习效果为“优秀”的学生为510名.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,从不同统计图中得到必要的信息是解决本题的关键.
19.(1)
最喜爱的项目 频数(人数) 所占百分比
篮球 56 28%
排球 24 12%
乒乓球 48 24%
健美操 30 15%
武术操 22 11%
跑步 20 10%
合计 200 100%
(2)喜爱篮球的最多,喜爱跑步的最少
【解析】略
20.(1)A、C
(2)由统计表数据可以看出,比赛33场,胜16场,胜场数大约50%,而美国比赛50场胜40场,胜场数是80%;日本比赛33场,胜14场,胜场数低于中国女足;从丢球数来看,同样多场比赛,丢球数远远少于日本女足;所以说,目前中国女足在亚洲还能算是一流强队,但在全世界排名,则是中上水平.(答案不唯一)
【分析】(1)根据各种统计图的特点作答即可;
(2)从胜场数和丢球数分析得出答案即可.
【详解】(1)解:根据表中数据,要清楚地反映不同国家女足比赛总场数的多少,适合的统计图是条形统计图;要清楚地反映同一国家女足胜场数、平局数、负场数在比赛总场数中所占的百分比,适合的统计图是扇形统计图;
故答案为:A、C;
(2)解:由统计表数据可以看出,比赛33场,胜16场,胜场数大约50%,而美国比赛50场胜40场,胜场数是80%;日本比赛33场,胜14场,胜场数低于中国女足;从丢球数来看,同样多场比赛,丢球数远远少于日本女足;所以说,目前中国女足在亚洲还能算是一流强队,但在全世界排名,则是中上水平.(答案不唯一)
【点睛】本题考查了统计图的特点,从条形统计图中很容易看出各种数量的多少;从折线统计图可以很容易看出统计数量的增减变化;扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
21.(1)调查的总体是:某校七年级的200名同学最喜欢的科目,调查的个体是:每一位同学最喜欢的科目
(2)
【分析】本题主要考查的是调查的相关知识,解题的关键是掌握调查的问题以及对象的确定方法;
(1)根据总体和个体的定义,结合题干描述,作答即可;
(2)根据被调查的200名学生中,有60人最喜欢学数学,列式计算即可.
【详解】(1)解:调查的总体是:某校七年级的200名同学最喜欢的科目,
调查的个体是:每一位同学最喜欢的科目;
(2)解:最喜欢学数学这门学科的学生占学生总数的百分比为:.
22.(1)200
(2)
(3)九年级学生身高在的人数约为150人
【分析】本题考查了条形统计图与扇形统计图的信息关联,求扇形统计图的圆心角,用样本的“率”估计总体的“率”,正确理解条形统计图与扇形统计图的信息关联是解答本题的关键.
(1)根据条形图可得,九年级1班,3班,5班学生的总数为(人),根据扇形统计图可得,1班,3班,5班学生的总数占九年级学生总数的,计算即可得出答案;
(2)根据九(2)班学生占九年级学生总数的,计算即可得出答案;
(3)根据用样本估计总体的计算方法即可得出答案.
【详解】(1)根据条形图可得,九年级1班,3班,5班学生的总数为(人),
根据扇形统计图可得,1班,3班,5班学生的总数占九年级学生总数的,
则九年级学生总数为(人),
故答案为:200;
(2)根据题意得,
故答案为:.
(3)根据题意得,九(2)班有(人),
则九年级学生身高在的人数约为(人).
23.小亮的方案比较好,理由见解析
【分析】本题考查了抽样调查中的样本应满足的条件,答题时要根据实际情况进行分析,把握住抽样调查所抽取的样本必须具有广泛性和代表性是解题的关键.根据抽样调查中的样本应满足的条件,即可解答.
【详解】小亮的方案比较好.理由如下:
小明的方案中的样本是自己所在班级同学的团史知识学习情况,样本的选取面太窄,不能代表其他班级同学的团史知识学习情况.
小亮的方案中抽取的样本具有广泛性和代表性,通过这样的抽样调查可以比较准确地推算出这二十四个班级同学的团史知识学习情况.
故小亮的方案比较好.
24.(1)
(2);
(3)
(4)
【分析】(1)用“书法”的人数除以其所占的百分比即可求出抽样调查的学生总人数;
(2)用“文学鉴赏”、“音乐舞蹈”的人数除以总人数即可求出、的值;
(3)用总人数乘以“国际象棋”的人数所占的百分比求出“国际象棋”的人数;
(4)用该校总人数乘以全校选择“音乐舞蹈”社团的学生所占的百分比即可.
【详解】(1)解:(1)本次抽样调查的学生总人数是:(人),
故答案为:.
(2),
,
故答案为:;.
(3)“国际象棋”的人数是:(人),
故答案为:.
(4)(人),
估计全校选择“音乐舞蹈”社团的学生有人,
故答案为:.
【点睛】本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章数据的收集、整理、描述
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为了解某校1500名学生的体重情况,从中抽取了100名学生的体重,就这个问题来说,下面说法正确的是( )
A.每个学生是个体 B.1500名学生是总体
C.1500名学生的体重是总体 D.100名学生是所抽取的一个样本
2.为了了解我校八年级的1200名学生的数学期中成绩,随机抽取80名学生的数学成绩进行分析,则下列说法错误的是( )
A.总体是我校八年级的1200名学生的数学期中成绩的全体
B.其中80名学生是总体的一个样本
C.样本容量是80
D.个体是我校八年级学生中每名学生数学期中成绩
3.2009年5月31日世界无烟日的口号是“戒烟一小时,健康亿人行”.小华学习小组为了解本地区大约有多少成年人吸烟,随机调查了100个成年人,结果其中有15个成年人吸烟.对于这个关于数据收集与描述的问题,下列说法正确的是( ).
A.调查的方式是普查 B.本地区只有85个成年人不吸烟
C.样本是15个吸烟的成年人 D.本地区约有的成年人吸烟
4.每年的3月21日是世界睡眠日,良好的睡眠状态是保持身体健康的重要基础,为了解某学校800名初一学生的睡眠时间,从21个班级中随机抽取50名学生进行调查,下列说法不正确的是( )
A.总体是该校800名初一学生的睡眠时间的全体
B.个体是每名初一学生的睡眠时间
C.样本是从中抽取的50名学生
D.样本容量是50
5.下列调查中,适合普查的是( )
A.调查某班级40名学生的身高情况
B.调查一批草莓的口感
C.调查盐城市人民对某政策的支持程度
D.了解全市学生桌椅的质量情况
6.2024年市有万名学生参加中考,为了了解这些考生的数学成绩,从中抽取200名考生的数学成绩进行统计分析,在这个问题中,下列说法:
①这万名考生的数学成绩是总体;
②每个考生是个体;
③200名考生是总体的一个样本;
④样本容量是200,
其中说法正确的有( )
A.4个 B.3个 C.2个 D.1个
7.为了解某校九年级400名学生的体重情况,从中随机抽取50名学生的体重进行分析,在这项调查中,样本是( )
A.400名学生 B.被抽取的50名学生
C.400名学生的体重 D.被抽取的50名学生的体重
8.某市教育局对七年级学生进行体质监测,共收集了名学生的体重数据,并绘制成频数分布直方图.若从左往右数每个小长方形的面积之比为,则其中第三组的频数为( )
A. B. C. D.
9.神舟十九号载人飞船在酒泉卫星发射中心点火发射,神舟十九号航天员乘组顺利进驻中国空间站,关于此次发射任务,不适合做全面调查的是( )
A.调查神舟十九号载人飞船的零部件是否符合标准
B.调查三位宇航员的身体状况
C.调查宇航员的太空服是否符合安全标准
D.调查神舟十九号载人飞船发射时的收视率
10.下列调查方式中适合的是( )
A.要了解一批节能灯的使用寿命,采用普查方式
B.调查你所在班级同学的身高,采用抽样调查方式
C.环保部门调查沱江某段水域的水质情况,采用抽样调查方式
D.调查全市中学生每天的就寝时间,采用普查方式
11.有60个数据,其中最大值为40,最小值为20.若取组距为5,则这组数据应该分成( )
A.3组 B.4组 C.5组 D.6组
12.养殖户老杨为了估计自己鱼塘1斤以上的鱼有多少条,老杨先从鱼塘里捞出了100条1斤以上的鱼做上标记,然后放回鱼塘里.经过一段时间,带有标记的鱼完全混合于鱼群后,老杨又从鱼塘捞出200条1斤以上的鱼,其中20条有标记,那么估计鱼塘里有1斤以上的鱼( )
A.1000条 B.2000条 C.3000条 D.4000条
二、填空题
13.“信阳毛尖”是中国十大名茶之一,其品牌价值逐年提升.近三年信阳毛尖的品牌价值如下:
年份 2021年 2022年 2023年
品牌价值 71.08亿元 75.72亿元 79.84亿元
小明和小聪根据统计表分别制作了如下的统计图:
你认为两个统计图给人不一样感觉的原因是 .
14.某地教育部门为了解本地区名中小学生(高中生人,初中生人,小学生人)的体质健康情况,计划进行抽样调查名学生,为了使调查具有代表性,初中生应随机抽取的学生数为 人.
15.将50个数据分成5组列出频数分布表,其中第一组的频数为6,第二组与第五组的频数之和为20,第三组的频率为0.2,则第四组的频率为 .
16.某次数学测验后,60分分这组人数占全班总人数的.若全班有50人,则该组的频数是 .
17.已知小鹏家五月份总支出共计元,用扇形统计图表示时,教育的支出所在的扇形的圆心角是度,那么其中用于教育上的支出是 .
三、解答题
18.为了解疫情期间学生网络学习的学习效果,我校随机抽取了九年级部分学生进行调查.调查结果分为四类:A类为“优秀”,B类为“良好”,C类为“一般”,D类为“不合格”,现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
(1)本次共调查了 ___________名学生;
(2)补全条形统计图:D类所对应扇形的圆心角的大小为 ___________;
(3)若我校九年级学生共有1700名,根据以上抽样结果,估计我校九年级学生学习效果为“优秀”的学生约有多少名?
19.我市教育局倡导中小学开展艺体普及活动,某校学生会为了了解全校同学对各项目的喜爱情况,随机调查了200名同学(每位同学仅选一项最喜爱的项目),根据调查结果制作了频数分布表:
最喜爱的项目 频数(人数) 所占百分比
篮球 28%
排球 24 12%
乒乓球 48 24%
健美操
武术操 22 11%
跑步 20 10%
合计 200 100%
(1)请补全频数分布表;
(2)在这次抽样调查中,喜爱哪个体育项目的同学最多?喜爱哪个体育项目的同学最少?
20.2022年2月6日,中国女足在决赛落后2球的不利局面下,顽强拼搏,最终3:2战胜韩国队,勇夺亚洲杯冠军!
晋级女足世界杯决赛圈3次及以上的国家队在女足世界杯决赛阶段的比赛结果统计
国家 胜场数 平局数 负场数 比赛总场数 进球数 丢球数
美国 40 6 4 50 138 38
德国 30 5 9 44 121 39
挪威 24 4 12 40 93 52
瑞典 32 5 12 49 71 48
巴西 20 4 10 34 66 40
中国 16 7 10 33 53 32
日本 14 4 15 33 39 55
(1)根据表中数据,要清楚地反映不同国家女足比赛总场数的多少,适合的统计图是 ;要清楚地反映同一国家女足胜场数、平局数、负场数在比赛总场数中所占的百分比,适合的统计图是 .(在空格上填写合适的代号)
A.条形统计图 B.折线统计图 C. 扇形统计图
(2)结合表中数据,从两个不同的角度简要评价中国女足的水平.
21.在数学、外语、语文3门学科中,某校七年级开展了同学们最喜欢学习哪门学科的调查(七年级共有200人).
(1)调查的总体和个体是什么?
(2)在被调查的200名学生中,有40人最喜欢学语文,60人最喜欢学数学,80人最喜欢学外语,其余的人选择其他,求最喜欢学数学这门学科的学生占学生总数的百分比.
22.5月初,某校组织九年级学生测量身高,该校九年级共有5个班,小华同学根据各班学生人数绘制了以下两幅统计图.
(1)该校九年级学生总数为 .
(2)请补全条形统计图,扇形统计图中“2班”所在扇形的圆心角的度数为 .
(3)九(2)班学生先一步测量身高,统计发现身高在的有30人,若该校九年级身高在的学生占比和九(2)班的占比情况相当,请估计九年级学生身高在的人数.
23.2022年是中国共产主义青年团建团100周年,某校团委组织全校二十四个班级同学开展主题为“成团百年,勇当先锋”的团史知识学习活动,为了解这二十四个班级的同学团史知识的学习情况,团里的小明、小亮分别设计了如下方案.
小明:调查出自己所在班级的每个同学的团史知识学习情况,以此推算出这二十四个班级同学的团史知识学习情况.
小亮:在这二十四个班级中,抽取学号为5的整数倍的72名同学,调查他们的团史知识学习情况,从而估计这二十四个班级同学的团史知识学习情况.
这两种方案哪一种比较好?请说明理由.
24.为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 文学鉴赏 国际象棋 音乐舞蹈 书法 其他
所占百分比
根据统计图表的信息,解答下列问题:
(1)本次抽样调查的学生有 人;
(2)统计表中的 , ;
(3)选择“国际象棋”的学生有 人;
(4)若该校共有名学生,试估计全校选择“音乐舞蹈”社团的学生有 人.
《第七章数据的收集、整理、描述》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D C A C D A D C
题号 11 12
答案 C A
1.C
【分析】总体是指考查的全体对象,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分考察对象.
【详解】A.、每个学生的体重是个体,错误;
B、1500名学生的体重是总体,错误;
C、1500名学生的体重是总体,正确;
D、100名学生的体重是所抽取的一个样本,错误.
故选:C..
【点睛】正确理解总体、个体、样本的概念是解决本题的关键.
2.B
【分析】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】解:A.总体是我校八年级的1200名学生的数学期中成绩的全体,说法正确,故本选项不符合题意;
B.其中80名学生的数学期中成绩是总体的一个样本,原说法错误,故本选项符合题意;
C.样本容量是80,说法正确,故本选项不符合题意;
D.个体是我校八年级学生中每名学生数学期中成绩,说法正确,故本选项不符合题意.
故选:B.
3.D
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:根据题意,随机调查100个成年人,是属于抽样调查,
这100个人中85人不吸烟不代表本地区只有85个成年人不吸烟,
样本是100个成年人,所以本地区约有的成年人吸烟是正确的.
故选:D.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.C
【分析】根据总体、个体、样本、样本容量之间的关系进行判断即可.
【详解】解:A、总体是该校800名初一学生的睡眠时间的全体,故选项正确,不符合题意;
B、个体是每名初一学生的睡眠时间,故选项正确,不符合题意;
C、从21个班级中随机抽取50名学生的睡眠时间是样本,故选项错误,符合题意;
D、样本容量是50,故选项正确,不符合题意;
故选:C.
【点睛】本题考查总体、个体、样本、样本容量,理解总体、样本、样本容量的意义是正确解答的关键.
5.A
【分析】根据适合普查的分式一般有一下几种:范围较小,易容掌控,不具有破坏性,可操作性强;即可进行判断.
【详解】解:A. 调查某班级40名学生的身高情况,应采用普查,此选项符合题意;
B. 调查一批草莓的口感,应选择抽样调查,此选项不合题意;
C. 调查盐城市人民对某政策的支持程度,应选择抽样调查,此选项不合题意;
D. 了解全市学生桌椅的质量情况,应选择抽样调查,此选项不合题意;
故选:A.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
6.C
【分析】本题考查总体、个体、样本、样本容量,理解总体、样本、样本容量的意义是正确解答的关键.
根据考查的对象是万名学生的中考数学成绩,利用总体、个体、样本、样本容量之间的关系进行判断即可.
【详解】解:这万名考生的数学成绩是总体,故①说法正确;
每个考生的数学成绩是个体,故②说法错误;
200名考生的数学成绩是总体的一个样本,故③说法错误;
样本容量是200故④说法正确;
所以,说法正确的有2个,
故选:C.
7.D
【分析】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
根据总体、个体、样本、样本容量的定义判断即可.
【详解】解:为了解某校九年级400名学生的体重情况,从中随机抽取50名学生的体重进行分析,在这项调查中,样本是被抽取的50名学生的体重.
故选:.
8.A
【分析】本题考查了频数分布直方图的性质,理解频数分布直方图的意义,掌握频率是解答本题的关键.
求出第三组的频数占被调查人数的百分比,再根据频率进行计算即可.
【详解】解:第三组的频数为,
故选:A.
9.D
【分析】本题考查的是全面调查和抽样调查,根据全面调查和抽样调查的概念判断即可.通过普查可以直接得到较为全面、可靠的信息,但花费的时间较长,耗费大,且一些调查项目并不适合普查.其一,调查者能力有限,不能进行普查.其二,调查过程带有破坏性.其三,有些被调查的对象无法进行普查.
【详解】解:A、查神舟十九号载人飞船的零部件是否符合标准,适合做全面调查,不符合题意;
B、调调查三位宇航员的身体状况,适合做全面调查,不符合题意;
C、调查宇航员的太空服是否符合安全标准,适合做全面调查,不符合题意;
D、调查神舟十九号载人飞船发射时的收视率,不适合做全面调查,符合题意.
故选:D.
10.C
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,逐项进行判断即可.
【详解】解:A.要了解一批节能灯的使用寿命,采用抽样调查,故A不符合题意;
B.调查你所在班级的同学的身高,应该采用普查,故B不符合题意;
C.环保部门调查沱江某段水域的水质情况,应该采用抽样调查,故C符合题意;
D.调查全市中学生每天的就寝时间,应该采用抽样调查,故D不符合题意.
故选:C.
【点睛】本题主要考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
11.C
【解析】略
12.A
【分析】用先从鱼塘里捞出的100条1斤以上的鱼的数量除以所抽样本中1斤以上的鱼所占比例即可.
【详解】解:估计鱼塘里有1斤以上的鱼有100÷=1000(条),
故选:A.
【点睛】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
13.两个统计图纵轴的单位长度不相同,且第一个统计图的纵轴不都是从0开始的
【分析】本题考查了条形统计图,根据两个统计图的纵轴的区别求解即可.
【详解】解:由图可得,两个统计图给人不一样感觉的原因是:两个统计图纵轴的单位长度不相同,且第一个统计图的纵轴不都是从0开始的,
故答案为:两个统计图纵轴的单位长度不相同,且第一个统计图的纵轴不都是从0开始的.
14.
【分析】利用抽取的百分比乘初中生的总数即可得.
【详解】解:(人),
故答案为:.
【点睛】本题考查了抽样调查,解题的关键是得出抽取比例.
15.0.28
【分析】本题考查了频数(率)分布表先计算出第三组的频数为10,再计算出第四组的频数为14,然后根据频率的定义计算第四组的频率.
【详解】解:第三组的频数为,
所以第四组的频数为,
所以第四组的频率.
故答案为0.28.
16.5
【分析】本题考查求频数,利用总数乘以频率进行求解即可.
【详解】解:;
故答案为:5.
17.元
【分析】本题考查了扇形统计图.根据圆心角的度数得出教育的支出的占比,乘以,即可求解.
【详解】解:依题意,其中用于教育上的支出为(元),
故答案为:元.
18.(1)50
(2)
(3)510
【分析】(1)根据类的人数和所占的百分比求出抽查的总人数.
(2)用总人数减去其他类别的人数,求出类的人数,从而补全条形图;用乘以类所占百分比即可得出类所对应的扇形圆心角度数.
(3)用总人数乘以九年级学生学习效果为“优秀” 的学生人数所占的百分比即可.
【详解】(1)这次一共抽取的学生有:
(名),
故答案为:50.
(2)类的人数有:(名),补全统计图如下:
扇形统计图中类所对应的扇形圆心角大小为:,
故答案为:.
(3)(名),
答:估计我校九年级学生学习效果为“优秀”的学生为510名.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,从不同统计图中得到必要的信息是解决本题的关键.
19.(1)
最喜爱的项目 频数(人数) 所占百分比
篮球 56 28%
排球 24 12%
乒乓球 48 24%
健美操 30 15%
武术操 22 11%
跑步 20 10%
合计 200 100%
(2)喜爱篮球的最多,喜爱跑步的最少
【解析】略
20.(1)A、C
(2)由统计表数据可以看出,比赛33场,胜16场,胜场数大约50%,而美国比赛50场胜40场,胜场数是80%;日本比赛33场,胜14场,胜场数低于中国女足;从丢球数来看,同样多场比赛,丢球数远远少于日本女足;所以说,目前中国女足在亚洲还能算是一流强队,但在全世界排名,则是中上水平.(答案不唯一)
【分析】(1)根据各种统计图的特点作答即可;
(2)从胜场数和丢球数分析得出答案即可.
【详解】(1)解:根据表中数据,要清楚地反映不同国家女足比赛总场数的多少,适合的统计图是条形统计图;要清楚地反映同一国家女足胜场数、平局数、负场数在比赛总场数中所占的百分比,适合的统计图是扇形统计图;
故答案为:A、C;
(2)解:由统计表数据可以看出,比赛33场,胜16场,胜场数大约50%,而美国比赛50场胜40场,胜场数是80%;日本比赛33场,胜14场,胜场数低于中国女足;从丢球数来看,同样多场比赛,丢球数远远少于日本女足;所以说,目前中国女足在亚洲还能算是一流强队,但在全世界排名,则是中上水平.(答案不唯一)
【点睛】本题考查了统计图的特点,从条形统计图中很容易看出各种数量的多少;从折线统计图可以很容易看出统计数量的增减变化;扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
21.(1)调查的总体是:某校七年级的200名同学最喜欢的科目,调查的个体是:每一位同学最喜欢的科目
(2)
【分析】本题主要考查的是调查的相关知识,解题的关键是掌握调查的问题以及对象的确定方法;
(1)根据总体和个体的定义,结合题干描述,作答即可;
(2)根据被调查的200名学生中,有60人最喜欢学数学,列式计算即可.
【详解】(1)解:调查的总体是:某校七年级的200名同学最喜欢的科目,
调查的个体是:每一位同学最喜欢的科目;
(2)解:最喜欢学数学这门学科的学生占学生总数的百分比为:.
22.(1)200
(2)
(3)九年级学生身高在的人数约为150人
【分析】本题考查了条形统计图与扇形统计图的信息关联,求扇形统计图的圆心角,用样本的“率”估计总体的“率”,正确理解条形统计图与扇形统计图的信息关联是解答本题的关键.
(1)根据条形图可得,九年级1班,3班,5班学生的总数为(人),根据扇形统计图可得,1班,3班,5班学生的总数占九年级学生总数的,计算即可得出答案;
(2)根据九(2)班学生占九年级学生总数的,计算即可得出答案;
(3)根据用样本估计总体的计算方法即可得出答案.
【详解】(1)根据条形图可得,九年级1班,3班,5班学生的总数为(人),
根据扇形统计图可得,1班,3班,5班学生的总数占九年级学生总数的,
则九年级学生总数为(人),
故答案为:200;
(2)根据题意得,
故答案为:.
(3)根据题意得,九(2)班有(人),
则九年级学生身高在的人数约为(人).
23.小亮的方案比较好,理由见解析
【分析】本题考查了抽样调查中的样本应满足的条件,答题时要根据实际情况进行分析,把握住抽样调查所抽取的样本必须具有广泛性和代表性是解题的关键.根据抽样调查中的样本应满足的条件,即可解答.
【详解】小亮的方案比较好.理由如下:
小明的方案中的样本是自己所在班级同学的团史知识学习情况,样本的选取面太窄,不能代表其他班级同学的团史知识学习情况.
小亮的方案中抽取的样本具有广泛性和代表性,通过这样的抽样调查可以比较准确地推算出这二十四个班级同学的团史知识学习情况.
故小亮的方案比较好.
24.(1)
(2);
(3)
(4)
【分析】(1)用“书法”的人数除以其所占的百分比即可求出抽样调查的学生总人数;
(2)用“文学鉴赏”、“音乐舞蹈”的人数除以总人数即可求出、的值;
(3)用总人数乘以“国际象棋”的人数所占的百分比求出“国际象棋”的人数;
(4)用该校总人数乘以全校选择“音乐舞蹈”社团的学生所占的百分比即可.
【详解】(1)解:(1)本次抽样调查的学生总人数是:(人),
故答案为:.
(2),
,
故答案为:;.
(3)“国际象棋”的人数是:(人),
故答案为:.
(4)(人),
估计全校选择“音乐舞蹈”社团的学生有人,
故答案为:.
【点睛】本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
