17.2函数的图像同步练习(含解析)
文档属性
| 名称 | 17.2函数的图像同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 21:45:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
17.2函数的图像
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知点A(a+1,4),B(3,2a+2),若直线AB∥x轴,则a的值为( )
A.2 B.1 C.-4 D.-3
2.在平面直角坐标系中,点在轴上,位于原点上方,距离原点2个单位长度,则点的坐标为( ).
A. B. C. D.
3.下列条件不能确定点的位置的是( )
A.第二阶梯教室6排3座 B.小岛北偏东30°,距离1600m
C.距离北京市180千米 D.位于东经114.8°,北纬40.8°
4.某次航展中,歼模型飞机在某内飞行的高度与时间之间的关系大致如图所示.下列结论错误的是( )
A.在范围内,飞机高度有两次
B.在范围内,飞机高度在不断下降
C.在范围内,飞机高度有四次
D.在范围内,飞机有二次连续攀升
5.乐乐和姐姐一起出去运动,两人同时从家出发.沿相同路线前行,途中姐姐有事返回.乐乐继续前行.5分钟后也原路返回,两人恰好同时到家,乐乐和姐姐在整个运动过程中离家的路程(米),(米)与运动时间x(分)之间的函数关系如图所示.下列结论中错误的是( )
A.两人前行过程中的速度为180米/分 B.m的值是15,n的值是2700
C.姐姐返回时的速度为90米/分 D.运动18分钟时,两人相距800米
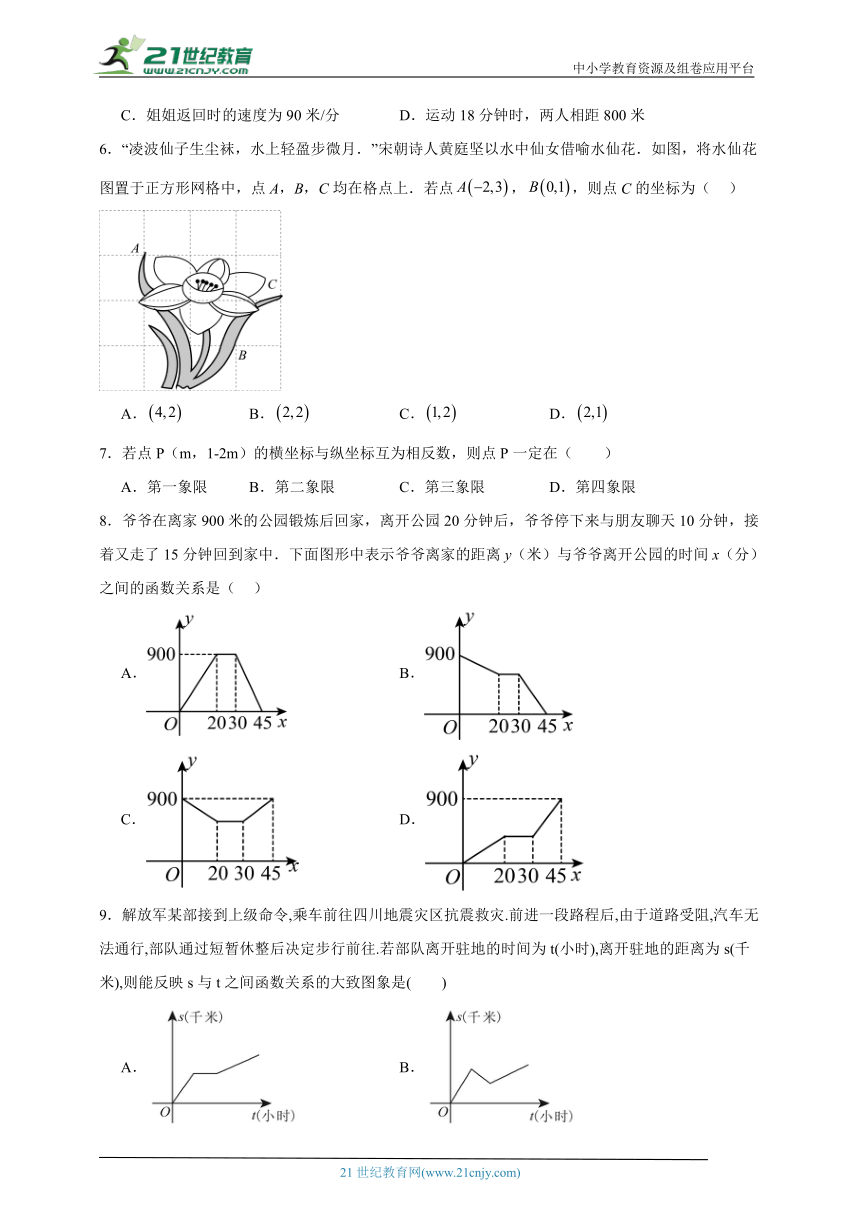
6.“凌波仙子生尘袜,水上轻盈步微月.”宋朝诗人黄庭坚以水中仙女借喻水仙花.如图,将水仙花图置于正方形网格中,点A,B,C均在格点上.若点,,则点C的坐标为( )
A. B. C. D.
7.若点P(m,1-2m)的横坐标与纵坐标互为相反数,则点P一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.爷爷在离家900米的公园锻炼后回家,离开公园20分钟后,爷爷停下来与朋友聊天10分钟,接着又走了15分钟回到家中.下面图形中表示爷爷离家的距离y(米)与爷爷离开公园的时间x(分)之间的函数关系是( )
A. B.
C. D.
9.解放军某部接到上级命令,乘车前往四川地震灾区抗震救灾.前进一段路程后,由于道路受阻,汽车无法通行,部队通过短暂休整后决定步行前往.若部队离开驻地的时间为t(小时),离开驻地的距离为s(千米),则能反映s与t之间函数关系的大致图象是( )
A. B.
C. D.
10.预备知识:线段中点坐标公式:在平面直角坐标系中,已知A(x1,y1),B(x2,y2),设点M为线段AB的中点,则点M的坐标为(,)应用:设线段CD的中点为点N,其坐标为(3,2),若端点C的坐标为(7,3),则端点D的坐标为( )
A.(﹣1,1) B.(﹣2,4) C.(﹣2,1) D.(﹣1,4)
11.在平面直角坐标系中.对于平面内任一点(m,n),规定以下两种变换:
①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(3,2)]等于( )
A.(3,2) B.(3.﹣2) C.(﹣3,2) D.(﹣3,﹣2)
12.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(2,0),第2次碰到正方形的边时的点为P2,…,第n次碰到正方形的边时的点为Pn,则点P2018的坐标是( )
A.(1,4) B.(4,3) C.(2,4) D.(4,1)
二、填空题
13.象限坐标特点:点P(x,y)分别在
①第一象限内,则x 0,y 0;
②第二象限内,则x 0,y 0;
③第三象限内,则x 0,y 0;
④第四象限内,则x 0,y 0.
14.甲、乙两个水桶内水面的高度y(cm)与放水(或注水)的时间x(分)之间关系的图象如图所示,当两个水桶内水面的高度相同时,x约为 分.(精确到0.1分)
15.由点A分别向 x轴,y轴作垂线,垂足M在x轴上的坐标是3,垂足N在 y轴上的坐标是4,有序数对(3,4)就叫做点A的 ,其中3是 ,4是 .
注意:表示点的坐标时,必须 在前, 在后,中间用 隔.
16.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头所示方向,每次移动一个单位长度,依次得到点,,,,,则点的坐标是 .
17.教材在第七章复习题的“拓广探索”中,曾让同学们探索发现:在平面直角坐标系中,线段中点的横坐标(纵坐标)分别等于对应线段的两个端点的横坐标(纵坐标)和的一半,例如:点,点,则线段的中点的坐标为,请利用以上结论解决问题:在平面直角坐标系中,点,若线段的中点恰好在轴上,且到轴的距离是,则 .
三、解答题
18.建立一个平面直角坐标系,描出点,,画直线.若点为直线上的任意一点,则点的纵坐标是什么?想一想:
(1)如果一些点在平行于轴的直线上,那么这些点的纵坐标有什么特点?
(2)如果一些点在平行于轴的直线上,那么这些点的横坐标有什么特点?
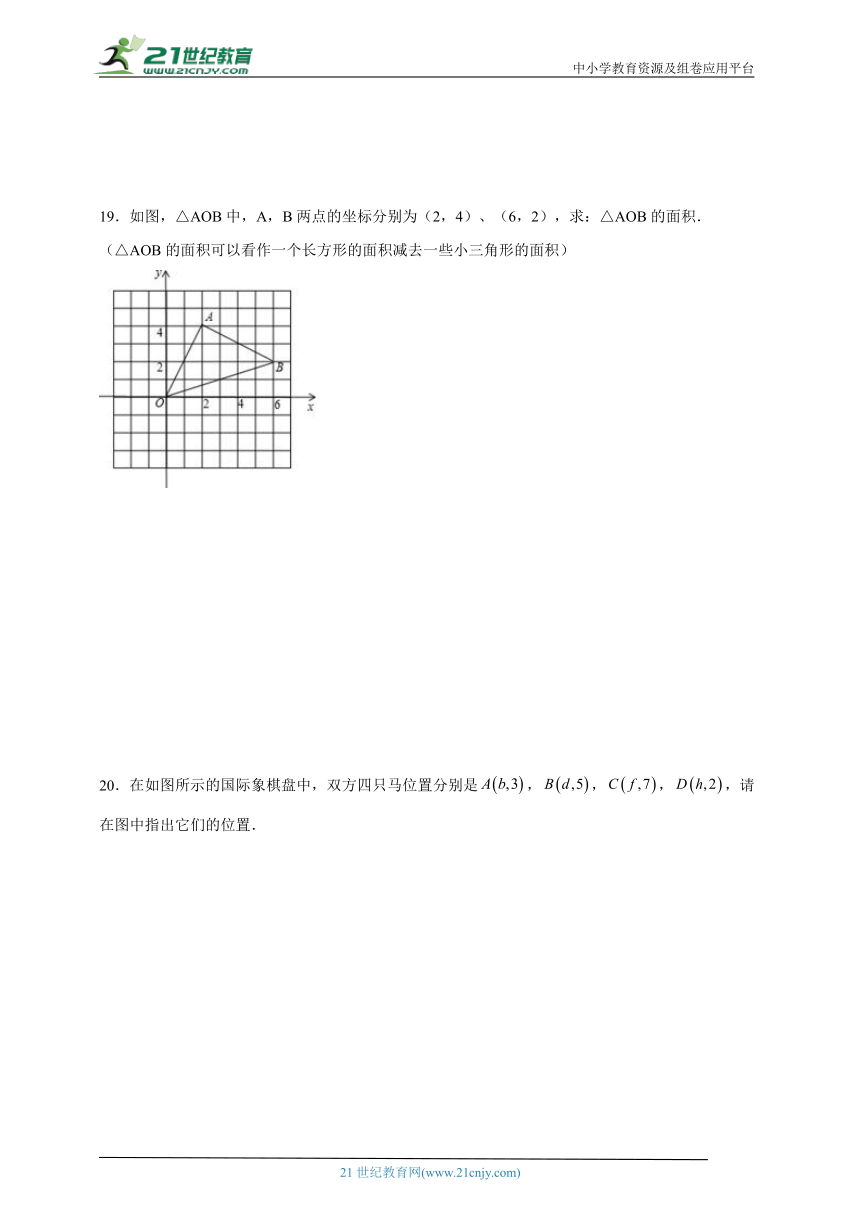
19.如图,△AOB中,A,B两点的坐标分别为(2,4)、(6,2),求:△AOB的面积.
(△AOB的面积可以看作一个长方形的面积减去一些小三角形的面积)
20.在如图所示的国际象棋盘中,双方四只马位置分别是,,,,请在图中指出它们的位置.
21.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同图反映了一天24小时内小明体温的变化情况:
(1)什么时间体温最低?什么时间体温最高?最低和最高体温各是多少?
(2)一天中小明体温T(单位:℃)的范围是多少.
(3)哪段时间小明的体温在上升,哪段时间体温在下降.
(4)请你说一说小明一天中体温的变化情况.
22.画出函数的图象,观察函数图象,请直接写出方程的根.
23.如图,在平面直角坐标系中,O为坐标原点.A、B两点的坐标分别为、,且,点P从A出发,以每秒1个单位的速度沿射线匀速运动,设点P运动时间为t秒.
(1)求、OB的长;
(2)连接,若的面积不大于3且不等于0,求t的范围;
(3)过P作直线AB的垂线,垂足为D,直线与y轴交于点E,在点P运动的过程中,是否存在这样的点P,使?若存在,请求出t的值;若不存在,请说明理由.
24.如图1,在平面直角坐标中,点,,,其中,点为线段上任意一点,连接,于,于.
(1)求证:;
(2)当时,若点,请你在图1中连接,交于点.求证:;
(3)若将“点为线段上任意一点”,改为“点为线段延长线上任意一点”,其他条件不变,连接,,垂足为,交轴于点,交轴于点,请在图2中补全图形,求点的坐标(用含的代数式表示).
《17.2函数的图像》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C C D C D B A A
题号 11 12
答案 C D
1.B
【详解】根据题意得:2a+2=4,解得:a=1.
故选:B
2.C
【分析】根据平面直角坐标系中点坐标的意义求解即可.
【详解】∵点在轴上,位于原点上方,距离原点2个单位长度,
∴点的横坐标为0,纵坐标为2,
即:点的坐标为,
故选:C.
【点睛】本题考查平面直角坐标系中点的坐标问题,理解在轴上的点的横坐标为0是解题关键
3.C
【分析】根据坐标确定位置需要两个数据对各选项分析判断后利用排除法求解.
【详解】解:A.第二阶梯教室6排3座的位置明确,故本选项不符合题意;
B.小岛北偏东30°,距离1600m的位置明确,故本选项不符合题意;
C.距离北京市180千米无法确定的具体位置,故本选项符合题意;
D.东经114.8°,北纬40.8°的位置明确,故本选项不符合题意;
故选:C.
【点睛】本题考查了坐标确定位置,理解位置的确定需要两个数据是解题的关键.
4.C
【分析】本题考查了函数的图像,解题的关键是数形结合.根据某一分钟内歼模型飞机高度与时间之间的函数图像逐项分析判断即可求解.
【详解】解:A、结合图像,在范围内,飞机高度有两次,故该选项正确,不符合题意;
B、结合图像,在范围内,飞机高度在不断下降,故该选项正确,不符合题意;
C、在范围内,飞机高度有三次,故该选项不正确,符合题意;
D、在范围内,飞机有二次连续攀升,故该选项正确,不符合题意;
故选:C.
5.D
【分析】根据题意和图象中的数据可以判断各选项中的说法是否正确,从而可以解答本题.
【详解】解:由图可得,两人前行过程中的速度为(米分),故选项不合题意;
的值是,的值是,故选项不合题意;
姐姐返回时的速度为:(米分),故选项不合题意;
运动18分钟时两人相距:(米,故选项符合题意,
故选:.
【点睛】本题考查一次函数的应用,明确题意,利用数形结合的思想解答是解答本题的关键.
6.C
【分析】本题考查了坐标与图形,根据题中给出的两点坐标建立坐标系即可得出C点坐标.
【详解】解:根据点,,建立直角坐标系如下图:
则,
故选:C.
7.D
【详解】m+(1-2m)=0,解得m=1,所以点P的坐标为(1,-1).故选D.
8.B
【分析】由题意,爷爷在公园回家,则当时,;从公园回家一共用了45分钟,则当时,;
【详解】解:由题意,爷爷在公园回家,则当时,;
从公园回家一共用了分钟,则当时,;
结合选项可知答案B.
故选B.
【点睛】本题考查函数图象;能够从题中获取信息,分析运动时间与距离之间的关系是解题的关键.
9.A
【详解】根据题意:分为3个阶段:1、前进一段路程后,位移增大;2、部队通过短暂休整,位移不变;3、部队步行前进,位移增大,但变慢;故选A.
10.A
【分析】根据线段的中点坐标公式即可得到结论.
【详解】设D(x,y),
由中点坐标公式得:=3,=2,
∴x=﹣1,y=1,
∴D(﹣1,1),
故选A.
【点睛】此题考查坐标与图形性质,关键是根据线段的中点坐标公式解答.
11.C
【分析】根据f、g的规定进行计算即可得解.
【详解】g[f(3,2)]=g(3,﹣2)=(﹣3,2).
故选C.
【点睛】本题考查了点的坐标,读懂题目信息,理解f、g的运算方法是解题的关键.
12.D
【分析】先根据反射角等于入射角先找出前几个点,直至出现规律,然后再根据规律进行求解.
【详解】由分析可得p(0,1)、、、、、、等,故该坐标的循环周期为7则有则有,故是第2018次碰到正方形的点的坐标为(4,1).
【点睛】本题主要考查规律的探索,注意观查规律是解题的关键.
13. ①>, >; ②<, >; ③<, <; ④>, <
【解析】略
14.2.7
【详解】如图所示,两个函数图象的交点的横坐标约为:2.7,所以当两个水桶内水面的高度相同时,时间约为2.7分钟.
故答案为2.7.
点睛:两个函数图象交点的横坐标就是两个水桶中水面高度相同的时间.
15. 坐标 横坐标 纵坐标 横坐标 纵坐标 逗号
【解析】略
16.
【分析】根据,,,…,得出,,即可得出的坐标.
【详解】解:由图可知:
∵,,,…,
∴,
∵,
∴;
故答案为:.
【点睛】本题考查坐标系下点的规律探究.根据图形,得到,是解题的关键.
17.或
【分析】根据线段的中点坐标公式即可得求出、的值,从而可得到答案.
【详解】解:∵点,,
∴中点,
∵中点恰好位于轴上,且到轴的距离是,
∴,
解得:或,
∴或,
故答案为:或.
【点睛】本题考查坐标与图形性质,中点坐标公式,二元一次方程组,运用了方程的思想.根据线段的中点坐标公式求出、的值是解题的关键.
18.见解析.点的纵坐标是4.(1)这些点的纵坐标相等;(2)这些点的横坐标相等.
【分析】分别根据平面直角坐标系上点坐标的特征即可得.
【详解】平面直角坐标系如图所示.点的纵坐标是4.
(1)这些点的纵坐标相等;
(2)这些点的横坐标相等.
【点睛】本题考查了平面直角坐标系点坐标规律,这是学习函数的基础.
19.10.
【分析】作辅助线(过点A、B分别作x轴、y轴的垂线CE、CF交点为C,垂足分别为E、F)构建矩形ECFO.根据矩形的四个角都是直角的性质求得矩形的面积、矩形ECFO中△AEO、△ABC、△BFO的面积,从而求得S△AOB=SECFO﹣S△AOE﹣S△ACB﹣S△BOF.
【详解】解:过点A、B分别作x轴、y轴的垂线CE、CF交点为C,垂足分别为E、F
∵A(2,4)、B(6,2)
∴OE=AC=4,EA=CB=BF=2,OF=6,
∴S△AOB=SECFO﹣S△AOE﹣S△ACB﹣S△BOF= 6×4-×4×2-×4×2-×6×2=24﹣4﹣4﹣6=10 ,
∴△AOB的面积是10.
【点睛】本题考查了三角形的面积、坐标与图形的性质.解答该题时,利用点的坐标求得相关线段的长度,然后根据图形的面积公式求解.
20.画图见解析
【分析】表示第列第行,从而可确定的位置,按同样的方法可确定的位置.
【详解】解:表示第列第行,表示第列第行,
表示第列第行,表示第列第行,
如图,
【点睛】本题考查的是利用有序实数对表示位置,根据有序实数对确定位置,正确理解表示第列第行是解题的关键.
21.(1)5时最低,17时最高,最低气温为36.5℃,最高气温为37.5℃.(2)36.5℃至37.5℃之间.(3)5时至17时体温上升,0时至5时和17时至24时体温在下降.(4)见解析
【分析】(1)根据图象进行作答即可;
(2)根据图象进行作答即可;
(3)根据图象进行作答即可;
(4)根据图象进行作答即可.
【详解】(1)5时最低,17时最高,最低气温为36.5℃,最高气温为37.5℃.
(2)36.5℃至37.5℃之间.
(3)5时至17时体温上升,0时至5时和17时至24时体温在下降.
(4)凌晨0至5时,小明体温在下降,5时体温最低是36.5℃;5至17时,小明体温在上升,17时体温最高是37.5℃;17至24时,小明体温在下降.
【点睛】本题考查了图象与变量的问题,掌握图象与变量的关系是解题的关键.
22.x1=-3,x2=1
【分析】求出图象与x轴交点坐标以及顶点坐标进而得出图象,利用图象得出方程的解即可.
【详解】y=x2+2x-3=(x+1)2-4,
∴图象的顶点为(-1,-4),
当y=0,则0=(x+1)2-4,
解得:x1=1,x2=-3,
∴图象与x轴交点坐标为:(1,0),(-3,0),
故函数图形如图所示:
观察图象,方程x2+2x-3=0的解为:x1=1,x2=-3.
【点睛】此题主要考查了二次函数图象的画法以及利用图象观察方程的解,利用数形结合得出是解题关键.
23.(1),
(2)且
(3)3或9
【分析】(1)根据绝对值的非负性和算术平方根的非负性求出m、n的值,即可得出答案;
(2)分两种情况进行讨论,用t表示出三角形的面积,然后分别求出t的取值范围即可;
(3)根据时,一定要使,然后分两种情况:P在线段上时或P在线段的延长线上进行讨论,求出t的值即可.
【详解】(1)解:∵,
∴,,
解得:,,
∴,;
(2)解:分为两种情况:①当P在线段上时,如图所示:
,,
∴的面积,
∵若的面积不大于3且不等于0,
∴,
解得:;
②当P在线段的延长线上时,如图所示:
∵,,
∴的面积,
∵若的面积不大于3且不等于0,
∴,
解得:;
即t的范围是且;
(3)解:∵,
∴,
分两种情况:①当P在线段上时,如图所示:
∵,
∴;
②当P在线段的延长线上时,如图所示:
∵,
∴;
即存在这样的点P,使,t的值是3或9.
【点睛】本题主要考查了绝对值的非负性和算术平方根的非负性,三角形面积的计算,三角形全等的判定和性质,解题的关键是熟练掌握绝对值的非负性和算术平方根的非负性,注意进行分类讨论.
24.(1)见解析;(2)见解析;(3)见解析,
【分析】(1)先根据点,,,得到,则由三线合一定理得到,,证明,推出即可证明,得到;
(2)先根据点,得到,则,再证明,即可利用SAS证明得到,再由,可以推出,即;
(3)同样先证明,推出,得到,即可得到,再由,,得到,则,推出.
【详解】证明:(1)如图1,∵点,,,
∴,
∵,
∴,
∵∠AOB=∠AOC=90°,
∴,
∴,
∵,,
∴
∴,
∴,
∴,
∴;
(2)如图2,由(1)得,
∴,
∵,点,
∴,
∴,
∵,,
∴,
∴,
又∵BE=AD,AC=BN,
∴
∴,
∵,
∴,
∴;
(3)如图3,由(1)得,,,,
∵,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,轴轴,
∴,
∵,
∴,
∴
∴,
∴点的坐标为.
【点睛】本题主要考查了坐标与图形,全等三角形的性质与判定,等腰直角三角形的性质与判定等等,解题的关键在于能够熟练掌握全等三角形的性质与判定条件.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
17.2函数的图像
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知点A(a+1,4),B(3,2a+2),若直线AB∥x轴,则a的值为( )
A.2 B.1 C.-4 D.-3
2.在平面直角坐标系中,点在轴上,位于原点上方,距离原点2个单位长度,则点的坐标为( ).
A. B. C. D.
3.下列条件不能确定点的位置的是( )
A.第二阶梯教室6排3座 B.小岛北偏东30°,距离1600m
C.距离北京市180千米 D.位于东经114.8°,北纬40.8°
4.某次航展中,歼模型飞机在某内飞行的高度与时间之间的关系大致如图所示.下列结论错误的是( )
A.在范围内,飞机高度有两次
B.在范围内,飞机高度在不断下降
C.在范围内,飞机高度有四次
D.在范围内,飞机有二次连续攀升
5.乐乐和姐姐一起出去运动,两人同时从家出发.沿相同路线前行,途中姐姐有事返回.乐乐继续前行.5分钟后也原路返回,两人恰好同时到家,乐乐和姐姐在整个运动过程中离家的路程(米),(米)与运动时间x(分)之间的函数关系如图所示.下列结论中错误的是( )
A.两人前行过程中的速度为180米/分 B.m的值是15,n的值是2700
C.姐姐返回时的速度为90米/分 D.运动18分钟时,两人相距800米
6.“凌波仙子生尘袜,水上轻盈步微月.”宋朝诗人黄庭坚以水中仙女借喻水仙花.如图,将水仙花图置于正方形网格中,点A,B,C均在格点上.若点,,则点C的坐标为( )
A. B. C. D.
7.若点P(m,1-2m)的横坐标与纵坐标互为相反数,则点P一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.爷爷在离家900米的公园锻炼后回家,离开公园20分钟后,爷爷停下来与朋友聊天10分钟,接着又走了15分钟回到家中.下面图形中表示爷爷离家的距离y(米)与爷爷离开公园的时间x(分)之间的函数关系是( )
A. B.
C. D.
9.解放军某部接到上级命令,乘车前往四川地震灾区抗震救灾.前进一段路程后,由于道路受阻,汽车无法通行,部队通过短暂休整后决定步行前往.若部队离开驻地的时间为t(小时),离开驻地的距离为s(千米),则能反映s与t之间函数关系的大致图象是( )
A. B.
C. D.
10.预备知识:线段中点坐标公式:在平面直角坐标系中,已知A(x1,y1),B(x2,y2),设点M为线段AB的中点,则点M的坐标为(,)应用:设线段CD的中点为点N,其坐标为(3,2),若端点C的坐标为(7,3),则端点D的坐标为( )
A.(﹣1,1) B.(﹣2,4) C.(﹣2,1) D.(﹣1,4)
11.在平面直角坐标系中.对于平面内任一点(m,n),规定以下两种变换:
①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(3,2)]等于( )
A.(3,2) B.(3.﹣2) C.(﹣3,2) D.(﹣3,﹣2)
12.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(2,0),第2次碰到正方形的边时的点为P2,…,第n次碰到正方形的边时的点为Pn,则点P2018的坐标是( )
A.(1,4) B.(4,3) C.(2,4) D.(4,1)
二、填空题
13.象限坐标特点:点P(x,y)分别在
①第一象限内,则x 0,y 0;
②第二象限内,则x 0,y 0;
③第三象限内,则x 0,y 0;
④第四象限内,则x 0,y 0.
14.甲、乙两个水桶内水面的高度y(cm)与放水(或注水)的时间x(分)之间关系的图象如图所示,当两个水桶内水面的高度相同时,x约为 分.(精确到0.1分)
15.由点A分别向 x轴,y轴作垂线,垂足M在x轴上的坐标是3,垂足N在 y轴上的坐标是4,有序数对(3,4)就叫做点A的 ,其中3是 ,4是 .
注意:表示点的坐标时,必须 在前, 在后,中间用 隔.
16.如图,在平面直角坐标系中,一动点从原点出发,沿着箭头所示方向,每次移动一个单位长度,依次得到点,,,,,则点的坐标是 .
17.教材在第七章复习题的“拓广探索”中,曾让同学们探索发现:在平面直角坐标系中,线段中点的横坐标(纵坐标)分别等于对应线段的两个端点的横坐标(纵坐标)和的一半,例如:点,点,则线段的中点的坐标为,请利用以上结论解决问题:在平面直角坐标系中,点,若线段的中点恰好在轴上,且到轴的距离是,则 .
三、解答题
18.建立一个平面直角坐标系,描出点,,画直线.若点为直线上的任意一点,则点的纵坐标是什么?想一想:
(1)如果一些点在平行于轴的直线上,那么这些点的纵坐标有什么特点?
(2)如果一些点在平行于轴的直线上,那么这些点的横坐标有什么特点?
19.如图,△AOB中,A,B两点的坐标分别为(2,4)、(6,2),求:△AOB的面积.
(△AOB的面积可以看作一个长方形的面积减去一些小三角形的面积)
20.在如图所示的国际象棋盘中,双方四只马位置分别是,,,,请在图中指出它们的位置.
21.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同图反映了一天24小时内小明体温的变化情况:
(1)什么时间体温最低?什么时间体温最高?最低和最高体温各是多少?
(2)一天中小明体温T(单位:℃)的范围是多少.
(3)哪段时间小明的体温在上升,哪段时间体温在下降.
(4)请你说一说小明一天中体温的变化情况.
22.画出函数的图象,观察函数图象,请直接写出方程的根.
23.如图,在平面直角坐标系中,O为坐标原点.A、B两点的坐标分别为、,且,点P从A出发,以每秒1个单位的速度沿射线匀速运动,设点P运动时间为t秒.
(1)求、OB的长;
(2)连接,若的面积不大于3且不等于0,求t的范围;
(3)过P作直线AB的垂线,垂足为D,直线与y轴交于点E,在点P运动的过程中,是否存在这样的点P,使?若存在,请求出t的值;若不存在,请说明理由.
24.如图1,在平面直角坐标中,点,,,其中,点为线段上任意一点,连接,于,于.
(1)求证:;
(2)当时,若点,请你在图1中连接,交于点.求证:;
(3)若将“点为线段上任意一点”,改为“点为线段延长线上任意一点”,其他条件不变,连接,,垂足为,交轴于点,交轴于点,请在图2中补全图形,求点的坐标(用含的代数式表示).
《17.2函数的图像》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C C D C D B A A
题号 11 12
答案 C D
1.B
【详解】根据题意得:2a+2=4,解得:a=1.
故选:B
2.C
【分析】根据平面直角坐标系中点坐标的意义求解即可.
【详解】∵点在轴上,位于原点上方,距离原点2个单位长度,
∴点的横坐标为0,纵坐标为2,
即:点的坐标为,
故选:C.
【点睛】本题考查平面直角坐标系中点的坐标问题,理解在轴上的点的横坐标为0是解题关键
3.C
【分析】根据坐标确定位置需要两个数据对各选项分析判断后利用排除法求解.
【详解】解:A.第二阶梯教室6排3座的位置明确,故本选项不符合题意;
B.小岛北偏东30°,距离1600m的位置明确,故本选项不符合题意;
C.距离北京市180千米无法确定的具体位置,故本选项符合题意;
D.东经114.8°,北纬40.8°的位置明确,故本选项不符合题意;
故选:C.
【点睛】本题考查了坐标确定位置,理解位置的确定需要两个数据是解题的关键.
4.C
【分析】本题考查了函数的图像,解题的关键是数形结合.根据某一分钟内歼模型飞机高度与时间之间的函数图像逐项分析判断即可求解.
【详解】解:A、结合图像,在范围内,飞机高度有两次,故该选项正确,不符合题意;
B、结合图像,在范围内,飞机高度在不断下降,故该选项正确,不符合题意;
C、在范围内,飞机高度有三次,故该选项不正确,符合题意;
D、在范围内,飞机有二次连续攀升,故该选项正确,不符合题意;
故选:C.
5.D
【分析】根据题意和图象中的数据可以判断各选项中的说法是否正确,从而可以解答本题.
【详解】解:由图可得,两人前行过程中的速度为(米分),故选项不合题意;
的值是,的值是,故选项不合题意;
姐姐返回时的速度为:(米分),故选项不合题意;
运动18分钟时两人相距:(米,故选项符合题意,
故选:.
【点睛】本题考查一次函数的应用,明确题意,利用数形结合的思想解答是解答本题的关键.
6.C
【分析】本题考查了坐标与图形,根据题中给出的两点坐标建立坐标系即可得出C点坐标.
【详解】解:根据点,,建立直角坐标系如下图:
则,
故选:C.
7.D
【详解】m+(1-2m)=0,解得m=1,所以点P的坐标为(1,-1).故选D.
8.B
【分析】由题意,爷爷在公园回家,则当时,;从公园回家一共用了45分钟,则当时,;
【详解】解:由题意,爷爷在公园回家,则当时,;
从公园回家一共用了分钟,则当时,;
结合选项可知答案B.
故选B.
【点睛】本题考查函数图象;能够从题中获取信息,分析运动时间与距离之间的关系是解题的关键.
9.A
【详解】根据题意:分为3个阶段:1、前进一段路程后,位移增大;2、部队通过短暂休整,位移不变;3、部队步行前进,位移增大,但变慢;故选A.
10.A
【分析】根据线段的中点坐标公式即可得到结论.
【详解】设D(x,y),
由中点坐标公式得:=3,=2,
∴x=﹣1,y=1,
∴D(﹣1,1),
故选A.
【点睛】此题考查坐标与图形性质,关键是根据线段的中点坐标公式解答.
11.C
【分析】根据f、g的规定进行计算即可得解.
【详解】g[f(3,2)]=g(3,﹣2)=(﹣3,2).
故选C.
【点睛】本题考查了点的坐标,读懂题目信息,理解f、g的运算方法是解题的关键.
12.D
【分析】先根据反射角等于入射角先找出前几个点,直至出现规律,然后再根据规律进行求解.
【详解】由分析可得p(0,1)、、、、、、等,故该坐标的循环周期为7则有则有,故是第2018次碰到正方形的点的坐标为(4,1).
【点睛】本题主要考查规律的探索,注意观查规律是解题的关键.
13. ①>, >; ②<, >; ③<, <; ④>, <
【解析】略
14.2.7
【详解】如图所示,两个函数图象的交点的横坐标约为:2.7,所以当两个水桶内水面的高度相同时,时间约为2.7分钟.
故答案为2.7.
点睛:两个函数图象交点的横坐标就是两个水桶中水面高度相同的时间.
15. 坐标 横坐标 纵坐标 横坐标 纵坐标 逗号
【解析】略
16.
【分析】根据,,,…,得出,,即可得出的坐标.
【详解】解:由图可知:
∵,,,…,
∴,
∵,
∴;
故答案为:.
【点睛】本题考查坐标系下点的规律探究.根据图形,得到,是解题的关键.
17.或
【分析】根据线段的中点坐标公式即可得求出、的值,从而可得到答案.
【详解】解:∵点,,
∴中点,
∵中点恰好位于轴上,且到轴的距离是,
∴,
解得:或,
∴或,
故答案为:或.
【点睛】本题考查坐标与图形性质,中点坐标公式,二元一次方程组,运用了方程的思想.根据线段的中点坐标公式求出、的值是解题的关键.
18.见解析.点的纵坐标是4.(1)这些点的纵坐标相等;(2)这些点的横坐标相等.
【分析】分别根据平面直角坐标系上点坐标的特征即可得.
【详解】平面直角坐标系如图所示.点的纵坐标是4.
(1)这些点的纵坐标相等;
(2)这些点的横坐标相等.
【点睛】本题考查了平面直角坐标系点坐标规律,这是学习函数的基础.
19.10.
【分析】作辅助线(过点A、B分别作x轴、y轴的垂线CE、CF交点为C,垂足分别为E、F)构建矩形ECFO.根据矩形的四个角都是直角的性质求得矩形的面积、矩形ECFO中△AEO、△ABC、△BFO的面积,从而求得S△AOB=SECFO﹣S△AOE﹣S△ACB﹣S△BOF.
【详解】解:过点A、B分别作x轴、y轴的垂线CE、CF交点为C,垂足分别为E、F
∵A(2,4)、B(6,2)
∴OE=AC=4,EA=CB=BF=2,OF=6,
∴S△AOB=SECFO﹣S△AOE﹣S△ACB﹣S△BOF= 6×4-×4×2-×4×2-×6×2=24﹣4﹣4﹣6=10 ,
∴△AOB的面积是10.
【点睛】本题考查了三角形的面积、坐标与图形的性质.解答该题时,利用点的坐标求得相关线段的长度,然后根据图形的面积公式求解.
20.画图见解析
【分析】表示第列第行,从而可确定的位置,按同样的方法可确定的位置.
【详解】解:表示第列第行,表示第列第行,
表示第列第行,表示第列第行,
如图,
【点睛】本题考查的是利用有序实数对表示位置,根据有序实数对确定位置,正确理解表示第列第行是解题的关键.
21.(1)5时最低,17时最高,最低气温为36.5℃,最高气温为37.5℃.(2)36.5℃至37.5℃之间.(3)5时至17时体温上升,0时至5时和17时至24时体温在下降.(4)见解析
【分析】(1)根据图象进行作答即可;
(2)根据图象进行作答即可;
(3)根据图象进行作答即可;
(4)根据图象进行作答即可.
【详解】(1)5时最低,17时最高,最低气温为36.5℃,最高气温为37.5℃.
(2)36.5℃至37.5℃之间.
(3)5时至17时体温上升,0时至5时和17时至24时体温在下降.
(4)凌晨0至5时,小明体温在下降,5时体温最低是36.5℃;5至17时,小明体温在上升,17时体温最高是37.5℃;17至24时,小明体温在下降.
【点睛】本题考查了图象与变量的问题,掌握图象与变量的关系是解题的关键.
22.x1=-3,x2=1
【分析】求出图象与x轴交点坐标以及顶点坐标进而得出图象,利用图象得出方程的解即可.
【详解】y=x2+2x-3=(x+1)2-4,
∴图象的顶点为(-1,-4),
当y=0,则0=(x+1)2-4,
解得:x1=1,x2=-3,
∴图象与x轴交点坐标为:(1,0),(-3,0),
故函数图形如图所示:
观察图象,方程x2+2x-3=0的解为:x1=1,x2=-3.
【点睛】此题主要考查了二次函数图象的画法以及利用图象观察方程的解,利用数形结合得出是解题关键.
23.(1),
(2)且
(3)3或9
【分析】(1)根据绝对值的非负性和算术平方根的非负性求出m、n的值,即可得出答案;
(2)分两种情况进行讨论,用t表示出三角形的面积,然后分别求出t的取值范围即可;
(3)根据时,一定要使,然后分两种情况:P在线段上时或P在线段的延长线上进行讨论,求出t的值即可.
【详解】(1)解:∵,
∴,,
解得:,,
∴,;
(2)解:分为两种情况:①当P在线段上时,如图所示:
,,
∴的面积,
∵若的面积不大于3且不等于0,
∴,
解得:;
②当P在线段的延长线上时,如图所示:
∵,,
∴的面积,
∵若的面积不大于3且不等于0,
∴,
解得:;
即t的范围是且;
(3)解:∵,
∴,
分两种情况:①当P在线段上时,如图所示:
∵,
∴;
②当P在线段的延长线上时,如图所示:
∵,
∴;
即存在这样的点P,使,t的值是3或9.
【点睛】本题主要考查了绝对值的非负性和算术平方根的非负性,三角形面积的计算,三角形全等的判定和性质,解题的关键是熟练掌握绝对值的非负性和算术平方根的非负性,注意进行分类讨论.
24.(1)见解析;(2)见解析;(3)见解析,
【分析】(1)先根据点,,,得到,则由三线合一定理得到,,证明,推出即可证明,得到;
(2)先根据点,得到,则,再证明,即可利用SAS证明得到,再由,可以推出,即;
(3)同样先证明,推出,得到,即可得到,再由,,得到,则,推出.
【详解】证明:(1)如图1,∵点,,,
∴,
∵,
∴,
∵∠AOB=∠AOC=90°,
∴,
∴,
∵,,
∴
∴,
∴,
∴,
∴;
(2)如图2,由(1)得,
∴,
∵,点,
∴,
∴,
∵,,
∴,
∴,
又∵BE=AD,AC=BN,
∴
∴,
∵,
∴,
∴;
(3)如图3,由(1)得,,,,
∵,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,轴轴,
∴,
∵,
∴,
∴
∴,
∴点的坐标为.
【点睛】本题主要考查了坐标与图形,全等三角形的性质与判定,等腰直角三角形的性质与判定等等,解题的关键在于能够熟练掌握全等三角形的性质与判定条件.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
