19.1矩形同步练习(含解析)
文档属性
| 名称 | 19.1矩形同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1013.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 21:51:51 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
19.1矩形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,在中,对角线与相交于点,添加一个条件后,为矩形,则这个条件可以是( )
A. B. C. D.
2.若直角三角形两条直角边的长分别为18和24,则斜边上的中线的长是( )
A.15 B.30 C. D.
3.下列叙述错误的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线相等
C.对角线互相平分的四边形是平行四边形 D.对角线相等的四边形是矩形
4.在数学活动课上,小明准备用绳子和三角尺检查一个书架是否为矩形.如图,已知书架是平行四边形,对角线,相交于点,下列验证方法错误的是( )
A. B. C. D.
5.下列选项中,矩形具有的性质是( )
A.四边相等 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
6.如图,图中的是将矩形沿对角线折叠得到的,图中(包括实线、虚线在内)共有全等三角形( )对.
A.1 B.2 C.3 D.4
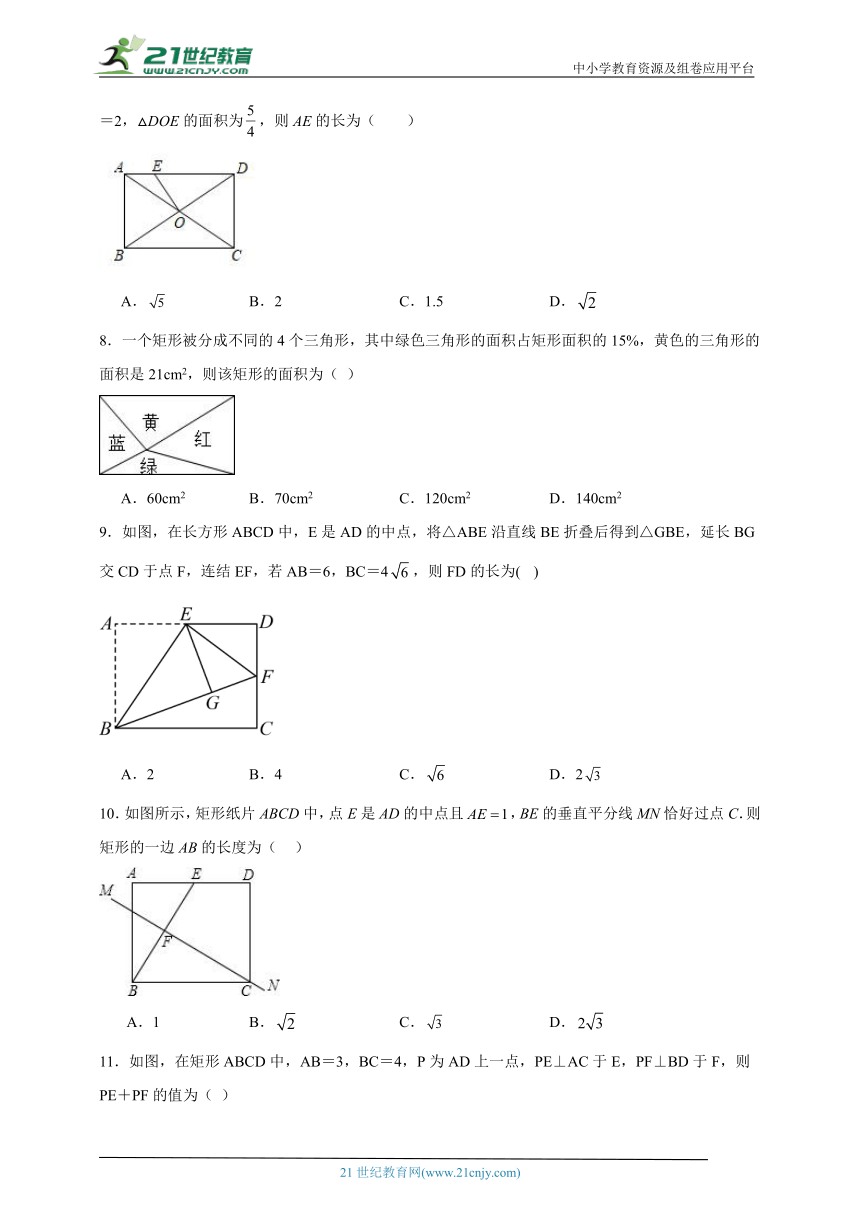
7.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为,则AE的长为( )
A. B.2 C.1.5 D.
8.一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
A.60cm2 B.70cm2 C.120cm2 D.140cm2
9.如图,在长方形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连结EF,若AB=6,BC=4,则FD的长为( )
A.2 B.4 C. D.2
10.如图所示,矩形纸片ABCD中,点E是AD的中点且,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为( )
A.1 B. C. D.
11.如图,在矩形ABCD中,AB=3,BC=4,P为AD上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )
A.
B.
C.2
D.
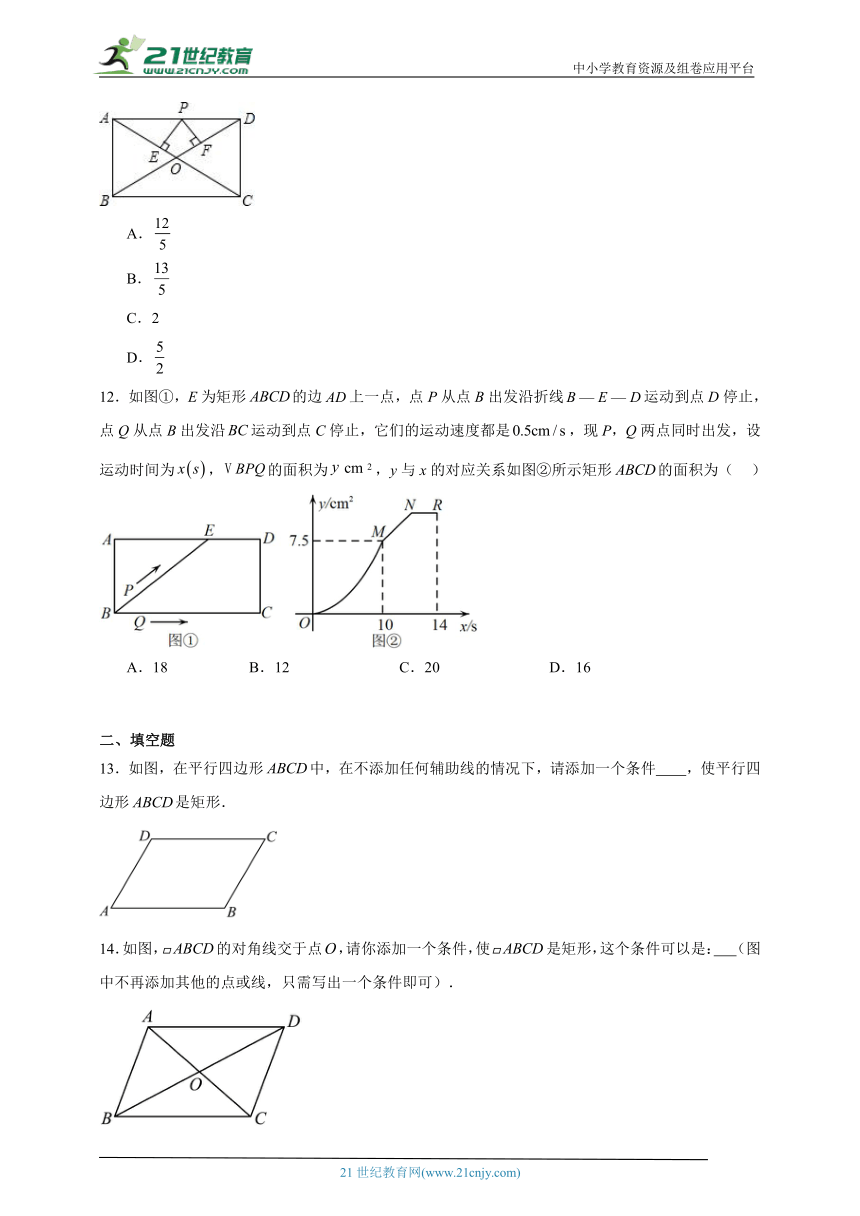
12.如图①,E为矩形的边上一点,点P从点B出发沿折线运动到点D停止,点Q从点B出发沿运动到点C停止,它们的运动速度都是,现P,Q两点同时出发,设运动时间为,的面积为,y与x的对应关系如图②所示矩形的面积为( )
A.18 B.12 C.20 D.16
二、填空题
13.如图,在平行四边形中,在不添加任何辅助线的情况下,请添加一个条件 ,使平行四边形是矩形.
14.如图,的对角线交于点,请你添加一个条件,使是矩形,这个条件可以是: (图中不再添加其他的点或线,只需写出一个条件即可).
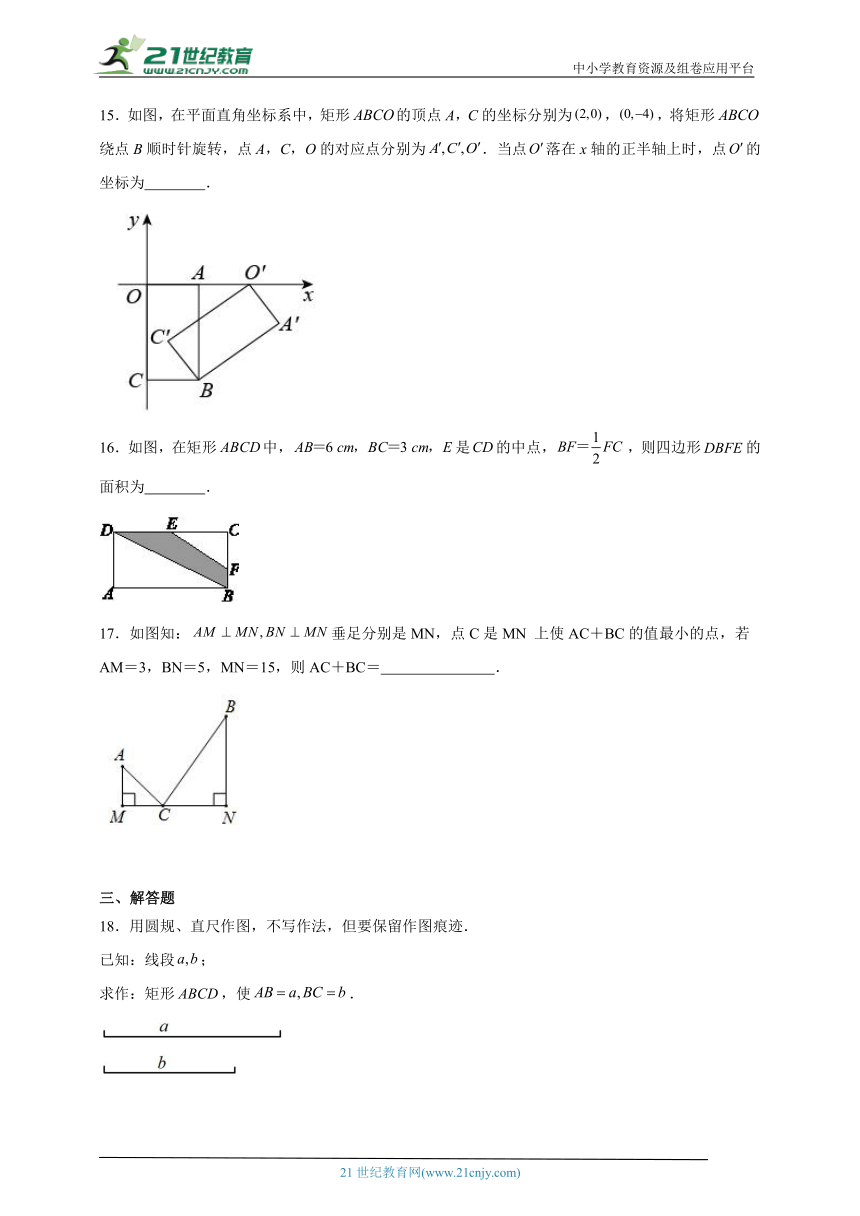
15.如图,在平面直角坐标系中,矩形的顶点A,C的坐标分别为,,将矩形绕点B顺时针旋转,点A,C,O的对应点分别为.当点落在x轴的正半轴上时,点的坐标为 .
16.如图,在矩形中,是的中点,,则四边形的面积为 .
17.如图知:垂足分别是MN,点C是MN 上使AC+BC的值最小的点,若AM=3,BN=5,MN=15,则AC+BC= .
三、解答题
18.用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:线段;
求作:矩形,使.
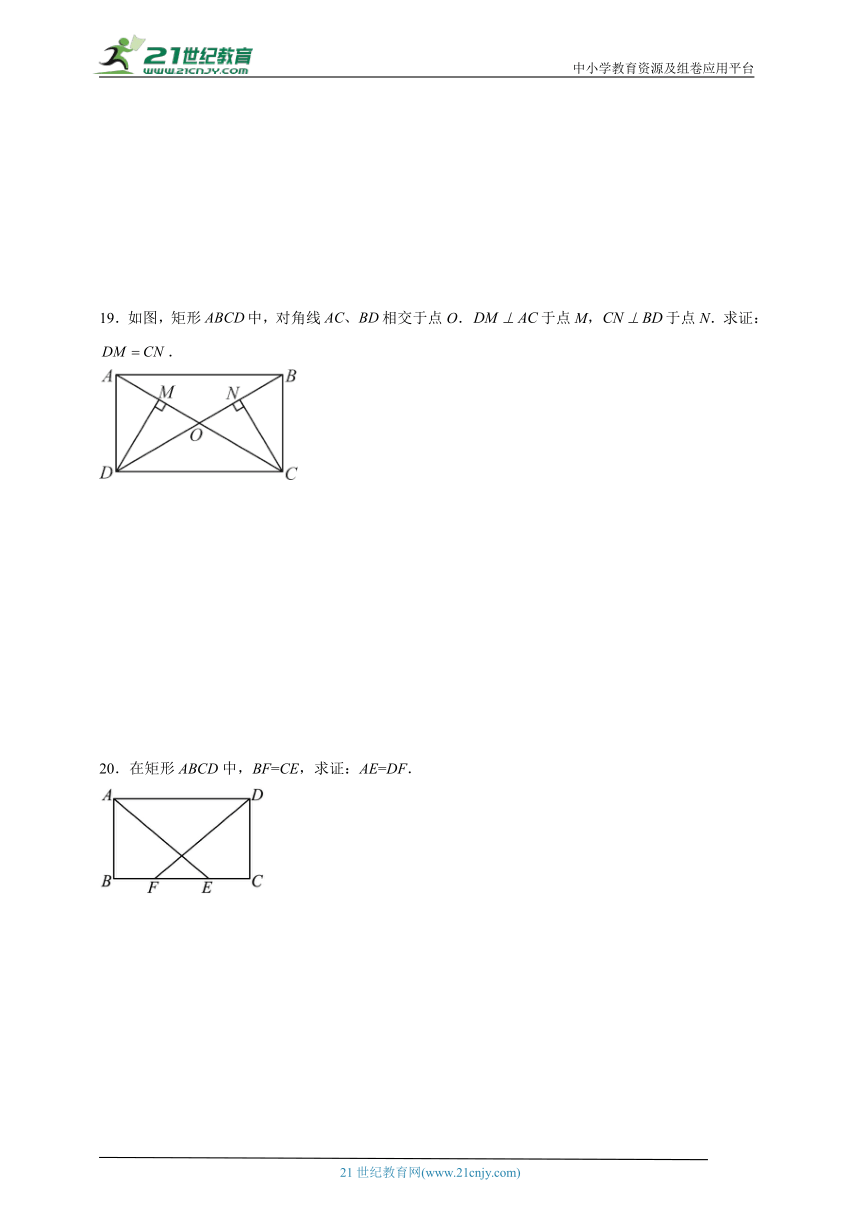
19.如图,矩形中,对角线相交于点O.于点M,于点N.求证:.
20.在矩形ABCD中,BF=CE,求证:AE=DF.
21.如图,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m.点A到地面的距离AE=1.5m,当他从A处摆动到A′时,有A′B⊥AB.
(1)求A′到BD的距离;
(2)求A′到地面的距离.
22.如图,在平行四边形中,对角线,相交于点O,且,.求的度数.
23.如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是.矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
(1)求点D的坐标;
(2)若点N是平面内任一点,在x轴上是否存在点M,使M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.
24.如图,已知平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过B点作AC的平行线,交CE的延长线于点F,连接BF.
(1)求证:FB=AO;
(2)平行四边形ABCD满足什么条件时,四边形AFBO是矩形?说明理由.
《19.1矩形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D D C D C A B C
题号 11 12
答案 A A
1.D
【分析】根据对角线相等的平行四边形是矩形判断即可.
【详解】解:添加对角线相等,即AC=BD,
理由是:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵AC=BD
∴是矩形,其它选项均不能得到矩形.
故选:D
【点睛】本题考查矩形的判断、平行四边形的性质等,解题的关键是熟练掌握基本知识,属于中考题型.
2.A
【分析】先根据勾股定理算出斜边长,再利用直角三角形斜边的中线等于斜边一半的性质得出即可.
【详解】∵直角三角形两条直角边的长分别为18和24,
∴直角三角形的斜边长为30,则斜边上的中线的长是15.故选A.
【点睛】本题考查直角三角形的性质,关键在于熟记斜边中线的性质.
3.D
【分析】由平行四边形的判定与性质、矩形的判定与性质分别对各个选项进行判断即可.
【详解】解:A、∵平行四边形的对角线互相平分,
∴选项A不符合题意;
B、∵矩形的对角线相等,
∴选项B不符合题意;
C、∵对角线互相平分的四边形是平行四边形,
∴选项C不符合题意;
D、∵对角线互相平分且相等的四边形是矩形,
∴选项D符合题意;
故选:D.
【点睛】本题考查了平行四边形的判定与性质、矩形的判定与性质;熟练掌握平行四边形的判定与性质、矩形的判定与性质是解题的关键.
4.D
【分析】本题主要考查了矩形的判定和平行四边形的性质,熟练掌握矩形的判定定理是解题的关键.根据矩形的判定方法进行判断即可.
【详解】解:∵,
∴.
∵四边形是平行四边形,
∴平行四边形是矩形,故A符合题意;
四边形是平行四边形,
,
,
,
平行四边形是矩形,故选项B不符合题意;
,四边形是平行四边形,
平行四边形是矩形,故选项C不符合题意;
由四边形是平行四边形,,不能判定平行四边形是矩形,故D符合题意.
故选D.
5.C
【分析】根据矩形的性质逐项分析即可.
【详解】A. 四边相等是菱形的性质,不是矩形的性质,故不符合题意;
B. 对角线互相垂直是菱形的性质,不是矩形的性质,故不符合题意;
C. 对角线相等是是矩形的性质,故符合题意;
D. 每条对角线平分一组对角是菱形的性质,不是矩形的性质,故不符合题意;
故选C.
【点睛】本题考查了矩形的性质:①矩形的对边平行且相等;②矩形的四个角都是直角;③矩形的对角线相等且互相平分;
6.D
【分析】根据对称的性质和全等三角形的概念求解即可.
【详解】如图,
由轴对称的性质可得;;;,
共有4对,
故选:D.
【点睛】此题考查了矩形的性质,折叠对称的性质,全等三角形的概念等知识,解题的关键是熟练掌握以上知识点.
7.C
【分析】首先连接BE,由题意可得OE为对角线BD的垂直平分线,可得BE=DE,S△BOE=S△DOE=,由三角形的面积则可求得DE的长,得出BE的长,然后由勾股定理求得答案.
【详解】连接BE,如图所示:
由题意可得,OE为对角线BD的垂直平分线,
∴BE=DE,S△BOE=S△DOE=,
∴S△BDE=2S△BOE=.
∴DE AB=,
又∵AB=2,
∴DE=,
∴BE=
在Rt△ABE中,由勾股定理得:AE=.
故选C.
【点睛】此题考查了矩形的性质、勾股定理以及三角形的面积问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
8.A
【详解】试题分析:黄色三角形与绿色三角形面积之和是矩形面积的50%,而绿色三角形面积占矩形面积的15%,所以黄色三角形面积占矩形面积的(50%-15%)=35%,已知黄色三角形面积是21平方厘米,故矩形的面积=21÷(50%-15%)=21÷35%=60(cm2).
故选A.
考点:矩形的性质.
9.B
【详解】试题分析:∵E是AD的中点,∴AE=DE,∵△ABE沿BE折叠后得到△GBE,∴AE=EG,AB=BG,∴ED=EG,∵在矩形ABCD中,∴∠A=∠D=90°,∴∠EGF=90°,在Rt△EDF和Rt△EGF中,∵ED=EG,EF=EF,∴Rt△EDF≌Rt△EGF(HL),∴DF=FG,设DF=x,则BF=6+x,CF=6﹣x,在Rt△BCF中,,解得x=4.故选B.
考点:1.翻折变换(折叠问题);2.综合题.
10.C
【分析】连接CE,首先利用线段垂直平分线的性质证明BC=EC,求出EC后根据勾股定理进一步计算即可.
【详解】如图,连接EC,
∵MN为BE的垂直平分线,
∴BC=EC,
∵点E是AD的中点且,
∴AE=DE=1,即AD=2,
∵四边形ABCD为矩形,
∴BC=AD=2,AB=CD,
∴EC=BC=2,
∴在Rt△EDC中,
CD=,
∴AB=CD=,
故选:C.
【点睛】本题主要考查了线段垂直平分线的性质以及勾股定理的运用,熟练掌握相关概念是解题关键.
11.A
【详解】由勾股定理求得矩形对角线AC的长为5,
过点A作AM⊥BD,垂足为M,
∴,则 .
连接PO,则有.
∵OA=OD,
∴,
故选A.
12.A
【分析】由题意知,运动分三段完成,运动10秒,P到点E,继续运动点Q到点C,点P自己运动到点D,结合图像信息求解即可.
【详解】解:由图象可知,时,P、E重合,
根据题意,得
,
∴,
解得,
∵四边形是矩形,
∴,
∴,
由图象可知,
∴,
∴,
∴矩形的面积为:
故选A.
【点睛】本题考查了矩形的性质,勾股定理,函数图象.熟练掌握矩形性质,从函数图象中获取正确的信息是解题的关键.
13.(答案不唯一)
【分析】本题考查的是矩形的判定,掌握矩形的判定是解题的关键.根据“有一个角是直角的平行四边形是矩形”填空.
【详解】解:添加条件:
理由:∵四边形是平行四边形,,
∴平行四边形是矩形(矩形的定义).
故答案是:(答案不唯一).
14.
【分析】根据矩形的判定定理在平行四边形的条件下,加上对角线相等,或者有一个角是直角即可
【详解】四边形是平行四边形
若
则四边形是矩形
故答案为:(答案不唯一)
【点睛】本题考查了矩形的判定定理,掌握矩形的判定定理是解题的关键.
15.
【分析】连接,,证明,可得,即可求解.
【详解】解:如图,连接,,
由题意得OA=BC=2,OC=AB=4,
由旋转可知,
在和中,
∴(HL),
∴,
∴坐标为(4,0),
故答案为:(4,0).
【点睛】本题考查了矩形的性质、旋转的性质和三角形全等的判定和性质,解题的关是证明.
16.
【分析】根据已知求出DC、CF、CE长,分别求出△BCD和△CEF的面积,即可求出答案.
【详解】在矩形中,是的中点,∠C=90°,.,四边形的面积.
故答案为:.
【点睛】本题考查矩形性质和三角形面积公式的计算.
17.17
【分析】以MN为轴作A点对称点A′,连接A′B交MN于C,则A′B就是AC+BC最小值;根据勾股定理求得A′B的长,即可求得AC+BC的最小值.
【详解】作A点关于直线MN的对称点A′,连接A′B交MN于C,则AC+BC=A′C+BC=A′B,A′B就是AC+BC的最小值;
延长BN使ND=A′M,连接A′D,
∵AM⊥MN,BN⊥MN,
∴AA′∥BD,
∴四边形A′DNM是矩形,
∴ND=AM=3,A′D=MN=15,
∴BD=BN+ND=5+3=8,
∴A′B=152+82=17,
∴AC+BC=17,
故答案为17.
【点睛】本题考查了轴对称 最短路线问题,涉及到的知识点有:轴对称的性质、矩形的判定和性质,勾股定理的应用等.
18.作图见详解
【分析】根据矩形的性质运用尺规作图即可.
【详解】解:(1)画射线,在上截取,即以点为圆心,以为半径画弧交于点,以点为圆心,以为半径画弧交于点;
(2)分别以点为圆心,以为半径,画弧,交于点,连接,以点为端点,在上取,
(3)分别以为圆心,为半径画弧,两弧交于点,连接,可得矩形,
如图所示,即为所求图形.
∴矩形即为所求图形.
【点睛】本题主要考查尺规作图,线段的垂直平分线的作图,矩形的作图,矩形的判定,掌握矩形的判定方法是解题的关键.
19.证明见解析.
【分析】本题考查了矩形的性质及全等三角形的判定及性质,利用矩形的性质及证得,进而可求证结论,熟练掌握相关判定及性质是解题的关键.
【详解】证明:∵四边形是矩形.
,,,
.
∵,,
.
在和中,
,
,
.
20.见解析
【分析】依据矩形的性质证明△ABE≌△DCF,即可得到结论.
【详解】证明:∵ 四边形ABCD是矩形,
∴,AB=CD.
∵BF=CE,
∴BF+EF=CE+EF,
∴ BE=CF.
∴△ABE≌△DCF.
∴AE=DF.
【点睛】此题考查矩形的性质的应用,三角形全等的判定及性质,熟记各定理是解题的关键.
21.(1)1m
(2)1m
【分析】(1)作A'F⊥BD,交BD于点F.设∠A'BF=∠1,∠BA'F=∠2,∠ABC=∠3.先证明△ACB≌△BFA'(AAS),则有A'F=BC,即有CD=AE;则可求出BC=BD﹣CD=1(m),即A'到BD的距离可求;
(2)作A'H⊥DE,交DE的延长线于点H.证得四边形A'HDF是矩形,则有A'H=FD,问题得解.
【详解】(1)(1)如图,作A'F⊥BD,交BD于点F,设∠A'BF=∠1,∠BA'F=∠3,∠ABC=∠2.
∵AC⊥BD,
∴∠ACB=∠A'FB=90°,
在Rt△A'FB中,∠1+∠3=90°,
又∵A'B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3;
在△ACB和△BFA'中,
,
∴△ACB≌△BFA'(AAS);
∴A'F=BC,
∵且CD⊥AC,AE⊥DE,
∴CD=AE=1.5;
∴BC=BD﹣CD=2.5﹣1.5=1(m),
∴A'F=1(m),
即A'到BD的距离是1m;
(2)由(1)知:△ACB≌△BFA',
∴BF=AC=1.5m,
如图,作A'H⊥DE,交DE的延长线于点H.
∵A'H⊥DE,BD⊥DE,
∵,
∴四边形A'HDF是矩形,
∴A'H=FD,
∴A'H=BD﹣BF=2.5﹣1.5=1(m),
A'即到地面的距离为1m.
【点睛】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
22.
【分析】本题考查了矩形的判定和性质、平行四边形的性质等知识,熟练掌握矩形的判定与性质是解此题的关键.
根据矩形的判定得到四边形是矩形,由矩形的性质求出,根据角的和差即可得出答案.
【详解】解:四边形是平行四边形,
,,
,
,
四边形是矩形,
,,
,
故的度数为.
23.(1);(2)存在,点M的坐标为或或或.
【分析】(1)由折叠的性质可得BE=AB=6,DE=AD,故OE=BO-BE=4,∠OED=90°,设D(0,a)则OD=a,DE=AD=OA-OD=8-a,在Rt△EOD中,由勾股定理得到方程即可求出a的值;
(2)分①OM,OE都为边;②OM为边OE为对角线;③OM为对角线,OE为边;3种情况进行讨论,分别求出M的坐标.
【详解】解:(1)四边形ABCO是矩形,点B的坐标是.
,,,
;
由折叠的性质得:,,,
,,
设,则,,
在中,由勾股定理得:,
即,解得:,
;
(2)存在,
①OM,OE都为边时,OM=OE=4,
∴M的坐标为(4,0),(-4,0)
②OM为边OE为对角线时,MN垂直平分OE,垂足为G,如图1
则OG=OE=2,
的解析式为:
设
(舍去),
由可得:
解得:
∴M(,0)
③OM为对角线,OE为边,如图2
由②得:M(,0)
综上所述:点M的坐标为或或或;
【点睛】此题主要考查四边形综合问题,解题的关键是熟知矩形的性质,折叠的问题利用勾股定理构造直角三角形进行求解,分情况讨论菱形的边及对角线的情况.
24.(1)证明见解析;(2)当平行四边形ABCD是菱形时,四边形AFBO是矩形.
【分析】(1)证明△BEF≌△OEC,即可得出结论;
(2)先证明四边形AFBO是平行四边形,然后根据OA⊥OB得到平行四边形AFBO是矩形.
【详解】证明:(1)∵E是BO的中点,
∴OE=BE,
∵BF∥AC,
∴∠BFE=∠OCE,
在△BEF和△OEC中,
∴△BEF≌△OEC,
∴BF=OC,
∵平行四边形ABCD的两条对角线相交于点O,
∴OA=OC,
∴FB=AO;
(2)当平行四边形ABCD是菱形时,四边形AFBO是矩形.理由如下:
∵BF∥AC,FB=AO,
∴四边形AFBO是平行四边形,
∵平行四边形ABCD是菱形,
∴OA⊥OB,
∴∠AOB=90°.
∴平行四边形AFBO是矩形.
【点睛】本题考查平行四边形的判定与性质以及菱形的性质、矩形的判定,熟练掌握相关判定定理和性质定理是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
19.1矩形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知,在中,对角线与相交于点,添加一个条件后,为矩形,则这个条件可以是( )
A. B. C. D.
2.若直角三角形两条直角边的长分别为18和24,则斜边上的中线的长是( )
A.15 B.30 C. D.
3.下列叙述错误的是( )
A.平行四边形的对角线互相平分 B.矩形的对角线相等
C.对角线互相平分的四边形是平行四边形 D.对角线相等的四边形是矩形
4.在数学活动课上,小明准备用绳子和三角尺检查一个书架是否为矩形.如图,已知书架是平行四边形,对角线,相交于点,下列验证方法错误的是( )
A. B. C. D.
5.下列选项中,矩形具有的性质是( )
A.四边相等 B.对角线互相垂直 C.对角线相等 D.每条对角线平分一组对角
6.如图,图中的是将矩形沿对角线折叠得到的,图中(包括实线、虚线在内)共有全等三角形( )对.
A.1 B.2 C.3 D.4
7.如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为,则AE的长为( )
A. B.2 C.1.5 D.
8.一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm2,则该矩形的面积为( )
A.60cm2 B.70cm2 C.120cm2 D.140cm2
9.如图,在长方形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,连结EF,若AB=6,BC=4,则FD的长为( )
A.2 B.4 C. D.2
10.如图所示,矩形纸片ABCD中,点E是AD的中点且,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为( )
A.1 B. C. D.
11.如图,在矩形ABCD中,AB=3,BC=4,P为AD上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )
A.
B.
C.2
D.
12.如图①,E为矩形的边上一点,点P从点B出发沿折线运动到点D停止,点Q从点B出发沿运动到点C停止,它们的运动速度都是,现P,Q两点同时出发,设运动时间为,的面积为,y与x的对应关系如图②所示矩形的面积为( )
A.18 B.12 C.20 D.16
二、填空题
13.如图,在平行四边形中,在不添加任何辅助线的情况下,请添加一个条件 ,使平行四边形是矩形.
14.如图,的对角线交于点,请你添加一个条件,使是矩形,这个条件可以是: (图中不再添加其他的点或线,只需写出一个条件即可).
15.如图,在平面直角坐标系中,矩形的顶点A,C的坐标分别为,,将矩形绕点B顺时针旋转,点A,C,O的对应点分别为.当点落在x轴的正半轴上时,点的坐标为 .
16.如图,在矩形中,是的中点,,则四边形的面积为 .
17.如图知:垂足分别是MN,点C是MN 上使AC+BC的值最小的点,若AM=3,BN=5,MN=15,则AC+BC= .
三、解答题
18.用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:线段;
求作:矩形,使.
19.如图,矩形中,对角线相交于点O.于点M,于点N.求证:.
20.在矩形ABCD中,BF=CE,求证:AE=DF.
21.如图,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m.点A到地面的距离AE=1.5m,当他从A处摆动到A′时,有A′B⊥AB.
(1)求A′到BD的距离;
(2)求A′到地面的距离.
22.如图,在平行四边形中,对角线,相交于点O,且,.求的度数.
23.如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是.矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
(1)求点D的坐标;
(2)若点N是平面内任一点,在x轴上是否存在点M,使M、N、E、O为顶点的四边形是菱形?若存在,请直接写出满足条件的点M的坐标;若不存在,请说明理由.
24.如图,已知平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过B点作AC的平行线,交CE的延长线于点F,连接BF.
(1)求证:FB=AO;
(2)平行四边形ABCD满足什么条件时,四边形AFBO是矩形?说明理由.
《19.1矩形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D D C D C A B C
题号 11 12
答案 A A
1.D
【分析】根据对角线相等的平行四边形是矩形判断即可.
【详解】解:添加对角线相等,即AC=BD,
理由是:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵AC=BD
∴是矩形,其它选项均不能得到矩形.
故选:D
【点睛】本题考查矩形的判断、平行四边形的性质等,解题的关键是熟练掌握基本知识,属于中考题型.
2.A
【分析】先根据勾股定理算出斜边长,再利用直角三角形斜边的中线等于斜边一半的性质得出即可.
【详解】∵直角三角形两条直角边的长分别为18和24,
∴直角三角形的斜边长为30,则斜边上的中线的长是15.故选A.
【点睛】本题考查直角三角形的性质,关键在于熟记斜边中线的性质.
3.D
【分析】由平行四边形的判定与性质、矩形的判定与性质分别对各个选项进行判断即可.
【详解】解:A、∵平行四边形的对角线互相平分,
∴选项A不符合题意;
B、∵矩形的对角线相等,
∴选项B不符合题意;
C、∵对角线互相平分的四边形是平行四边形,
∴选项C不符合题意;
D、∵对角线互相平分且相等的四边形是矩形,
∴选项D符合题意;
故选:D.
【点睛】本题考查了平行四边形的判定与性质、矩形的判定与性质;熟练掌握平行四边形的判定与性质、矩形的判定与性质是解题的关键.
4.D
【分析】本题主要考查了矩形的判定和平行四边形的性质,熟练掌握矩形的判定定理是解题的关键.根据矩形的判定方法进行判断即可.
【详解】解:∵,
∴.
∵四边形是平行四边形,
∴平行四边形是矩形,故A符合题意;
四边形是平行四边形,
,
,
,
平行四边形是矩形,故选项B不符合题意;
,四边形是平行四边形,
平行四边形是矩形,故选项C不符合题意;
由四边形是平行四边形,,不能判定平行四边形是矩形,故D符合题意.
故选D.
5.C
【分析】根据矩形的性质逐项分析即可.
【详解】A. 四边相等是菱形的性质,不是矩形的性质,故不符合题意;
B. 对角线互相垂直是菱形的性质,不是矩形的性质,故不符合题意;
C. 对角线相等是是矩形的性质,故符合题意;
D. 每条对角线平分一组对角是菱形的性质,不是矩形的性质,故不符合题意;
故选C.
【点睛】本题考查了矩形的性质:①矩形的对边平行且相等;②矩形的四个角都是直角;③矩形的对角线相等且互相平分;
6.D
【分析】根据对称的性质和全等三角形的概念求解即可.
【详解】如图,
由轴对称的性质可得;;;,
共有4对,
故选:D.
【点睛】此题考查了矩形的性质,折叠对称的性质,全等三角形的概念等知识,解题的关键是熟练掌握以上知识点.
7.C
【分析】首先连接BE,由题意可得OE为对角线BD的垂直平分线,可得BE=DE,S△BOE=S△DOE=,由三角形的面积则可求得DE的长,得出BE的长,然后由勾股定理求得答案.
【详解】连接BE,如图所示:
由题意可得,OE为对角线BD的垂直平分线,
∴BE=DE,S△BOE=S△DOE=,
∴S△BDE=2S△BOE=.
∴DE AB=,
又∵AB=2,
∴DE=,
∴BE=
在Rt△ABE中,由勾股定理得:AE=.
故选C.
【点睛】此题考查了矩形的性质、勾股定理以及三角形的面积问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
8.A
【详解】试题分析:黄色三角形与绿色三角形面积之和是矩形面积的50%,而绿色三角形面积占矩形面积的15%,所以黄色三角形面积占矩形面积的(50%-15%)=35%,已知黄色三角形面积是21平方厘米,故矩形的面积=21÷(50%-15%)=21÷35%=60(cm2).
故选A.
考点:矩形的性质.
9.B
【详解】试题分析:∵E是AD的中点,∴AE=DE,∵△ABE沿BE折叠后得到△GBE,∴AE=EG,AB=BG,∴ED=EG,∵在矩形ABCD中,∴∠A=∠D=90°,∴∠EGF=90°,在Rt△EDF和Rt△EGF中,∵ED=EG,EF=EF,∴Rt△EDF≌Rt△EGF(HL),∴DF=FG,设DF=x,则BF=6+x,CF=6﹣x,在Rt△BCF中,,解得x=4.故选B.
考点:1.翻折变换(折叠问题);2.综合题.
10.C
【分析】连接CE,首先利用线段垂直平分线的性质证明BC=EC,求出EC后根据勾股定理进一步计算即可.
【详解】如图,连接EC,
∵MN为BE的垂直平分线,
∴BC=EC,
∵点E是AD的中点且,
∴AE=DE=1,即AD=2,
∵四边形ABCD为矩形,
∴BC=AD=2,AB=CD,
∴EC=BC=2,
∴在Rt△EDC中,
CD=,
∴AB=CD=,
故选:C.
【点睛】本题主要考查了线段垂直平分线的性质以及勾股定理的运用,熟练掌握相关概念是解题关键.
11.A
【详解】由勾股定理求得矩形对角线AC的长为5,
过点A作AM⊥BD,垂足为M,
∴,则 .
连接PO,则有.
∵OA=OD,
∴,
故选A.
12.A
【分析】由题意知,运动分三段完成,运动10秒,P到点E,继续运动点Q到点C,点P自己运动到点D,结合图像信息求解即可.
【详解】解:由图象可知,时,P、E重合,
根据题意,得
,
∴,
解得,
∵四边形是矩形,
∴,
∴,
由图象可知,
∴,
∴,
∴矩形的面积为:
故选A.
【点睛】本题考查了矩形的性质,勾股定理,函数图象.熟练掌握矩形性质,从函数图象中获取正确的信息是解题的关键.
13.(答案不唯一)
【分析】本题考查的是矩形的判定,掌握矩形的判定是解题的关键.根据“有一个角是直角的平行四边形是矩形”填空.
【详解】解:添加条件:
理由:∵四边形是平行四边形,,
∴平行四边形是矩形(矩形的定义).
故答案是:(答案不唯一).
14.
【分析】根据矩形的判定定理在平行四边形的条件下,加上对角线相等,或者有一个角是直角即可
【详解】四边形是平行四边形
若
则四边形是矩形
故答案为:(答案不唯一)
【点睛】本题考查了矩形的判定定理,掌握矩形的判定定理是解题的关键.
15.
【分析】连接,,证明,可得,即可求解.
【详解】解:如图,连接,,
由题意得OA=BC=2,OC=AB=4,
由旋转可知,
在和中,
∴(HL),
∴,
∴坐标为(4,0),
故答案为:(4,0).
【点睛】本题考查了矩形的性质、旋转的性质和三角形全等的判定和性质,解题的关是证明.
16.
【分析】根据已知求出DC、CF、CE长,分别求出△BCD和△CEF的面积,即可求出答案.
【详解】在矩形中,是的中点,∠C=90°,.,四边形的面积.
故答案为:.
【点睛】本题考查矩形性质和三角形面积公式的计算.
17.17
【分析】以MN为轴作A点对称点A′,连接A′B交MN于C,则A′B就是AC+BC最小值;根据勾股定理求得A′B的长,即可求得AC+BC的最小值.
【详解】作A点关于直线MN的对称点A′,连接A′B交MN于C,则AC+BC=A′C+BC=A′B,A′B就是AC+BC的最小值;
延长BN使ND=A′M,连接A′D,
∵AM⊥MN,BN⊥MN,
∴AA′∥BD,
∴四边形A′DNM是矩形,
∴ND=AM=3,A′D=MN=15,
∴BD=BN+ND=5+3=8,
∴A′B=152+82=17,
∴AC+BC=17,
故答案为17.
【点睛】本题考查了轴对称 最短路线问题,涉及到的知识点有:轴对称的性质、矩形的判定和性质,勾股定理的应用等.
18.作图见详解
【分析】根据矩形的性质运用尺规作图即可.
【详解】解:(1)画射线,在上截取,即以点为圆心,以为半径画弧交于点,以点为圆心,以为半径画弧交于点;
(2)分别以点为圆心,以为半径,画弧,交于点,连接,以点为端点,在上取,
(3)分别以为圆心,为半径画弧,两弧交于点,连接,可得矩形,
如图所示,即为所求图形.
∴矩形即为所求图形.
【点睛】本题主要考查尺规作图,线段的垂直平分线的作图,矩形的作图,矩形的判定,掌握矩形的判定方法是解题的关键.
19.证明见解析.
【分析】本题考查了矩形的性质及全等三角形的判定及性质,利用矩形的性质及证得,进而可求证结论,熟练掌握相关判定及性质是解题的关键.
【详解】证明:∵四边形是矩形.
,,,
.
∵,,
.
在和中,
,
,
.
20.见解析
【分析】依据矩形的性质证明△ABE≌△DCF,即可得到结论.
【详解】证明:∵ 四边形ABCD是矩形,
∴,AB=CD.
∵BF=CE,
∴BF+EF=CE+EF,
∴ BE=CF.
∴△ABE≌△DCF.
∴AE=DF.
【点睛】此题考查矩形的性质的应用,三角形全等的判定及性质,熟记各定理是解题的关键.
21.(1)1m
(2)1m
【分析】(1)作A'F⊥BD,交BD于点F.设∠A'BF=∠1,∠BA'F=∠2,∠ABC=∠3.先证明△ACB≌△BFA'(AAS),则有A'F=BC,即有CD=AE;则可求出BC=BD﹣CD=1(m),即A'到BD的距离可求;
(2)作A'H⊥DE,交DE的延长线于点H.证得四边形A'HDF是矩形,则有A'H=FD,问题得解.
【详解】(1)(1)如图,作A'F⊥BD,交BD于点F,设∠A'BF=∠1,∠BA'F=∠3,∠ABC=∠2.
∵AC⊥BD,
∴∠ACB=∠A'FB=90°,
在Rt△A'FB中,∠1+∠3=90°,
又∵A'B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3;
在△ACB和△BFA'中,
,
∴△ACB≌△BFA'(AAS);
∴A'F=BC,
∵且CD⊥AC,AE⊥DE,
∴CD=AE=1.5;
∴BC=BD﹣CD=2.5﹣1.5=1(m),
∴A'F=1(m),
即A'到BD的距离是1m;
(2)由(1)知:△ACB≌△BFA',
∴BF=AC=1.5m,
如图,作A'H⊥DE,交DE的延长线于点H.
∵A'H⊥DE,BD⊥DE,
∵,
∴四边形A'HDF是矩形,
∴A'H=FD,
∴A'H=BD﹣BF=2.5﹣1.5=1(m),
A'即到地面的距离为1m.
【点睛】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
22.
【分析】本题考查了矩形的判定和性质、平行四边形的性质等知识,熟练掌握矩形的判定与性质是解此题的关键.
根据矩形的判定得到四边形是矩形,由矩形的性质求出,根据角的和差即可得出答案.
【详解】解:四边形是平行四边形,
,,
,
,
四边形是矩形,
,,
,
故的度数为.
23.(1);(2)存在,点M的坐标为或或或.
【分析】(1)由折叠的性质可得BE=AB=6,DE=AD,故OE=BO-BE=4,∠OED=90°,设D(0,a)则OD=a,DE=AD=OA-OD=8-a,在Rt△EOD中,由勾股定理得到方程即可求出a的值;
(2)分①OM,OE都为边;②OM为边OE为对角线;③OM为对角线,OE为边;3种情况进行讨论,分别求出M的坐标.
【详解】解:(1)四边形ABCO是矩形,点B的坐标是.
,,,
;
由折叠的性质得:,,,
,,
设,则,,
在中,由勾股定理得:,
即,解得:,
;
(2)存在,
①OM,OE都为边时,OM=OE=4,
∴M的坐标为(4,0),(-4,0)
②OM为边OE为对角线时,MN垂直平分OE,垂足为G,如图1
则OG=OE=2,
的解析式为:
设
(舍去),
由可得:
解得:
∴M(,0)
③OM为对角线,OE为边,如图2
由②得:M(,0)
综上所述:点M的坐标为或或或;
【点睛】此题主要考查四边形综合问题,解题的关键是熟知矩形的性质,折叠的问题利用勾股定理构造直角三角形进行求解,分情况讨论菱形的边及对角线的情况.
24.(1)证明见解析;(2)当平行四边形ABCD是菱形时,四边形AFBO是矩形.
【分析】(1)证明△BEF≌△OEC,即可得出结论;
(2)先证明四边形AFBO是平行四边形,然后根据OA⊥OB得到平行四边形AFBO是矩形.
【详解】证明:(1)∵E是BO的中点,
∴OE=BE,
∵BF∥AC,
∴∠BFE=∠OCE,
在△BEF和△OEC中,
∴△BEF≌△OEC,
∴BF=OC,
∵平行四边形ABCD的两条对角线相交于点O,
∴OA=OC,
∴FB=AO;
(2)当平行四边形ABCD是菱形时,四边形AFBO是矩形.理由如下:
∵BF∥AC,FB=AO,
∴四边形AFBO是平行四边形,
∵平行四边形ABCD是菱形,
∴OA⊥OB,
∴∠AOB=90°.
∴平行四边形AFBO是矩形.
【点睛】本题考查平行四边形的判定与性质以及菱形的性质、矩形的判定,熟练掌握相关判定定理和性质定理是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
