19.3正方形同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
19.3正方形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.正方形的对角线长为2,则其面积为( )
A.1 B.2 C.3 D.4
2.下列说法中正确的是( )
A.对角线相等且有一个角是直角的平行四边形是正方形
B.对角线互相垂直且一组邻边相等的平行四边形是正方形
C.四个角都相等的菱形是正方形
D.对角线互相垂直平分且有一组邻边相等的四边形是正方形
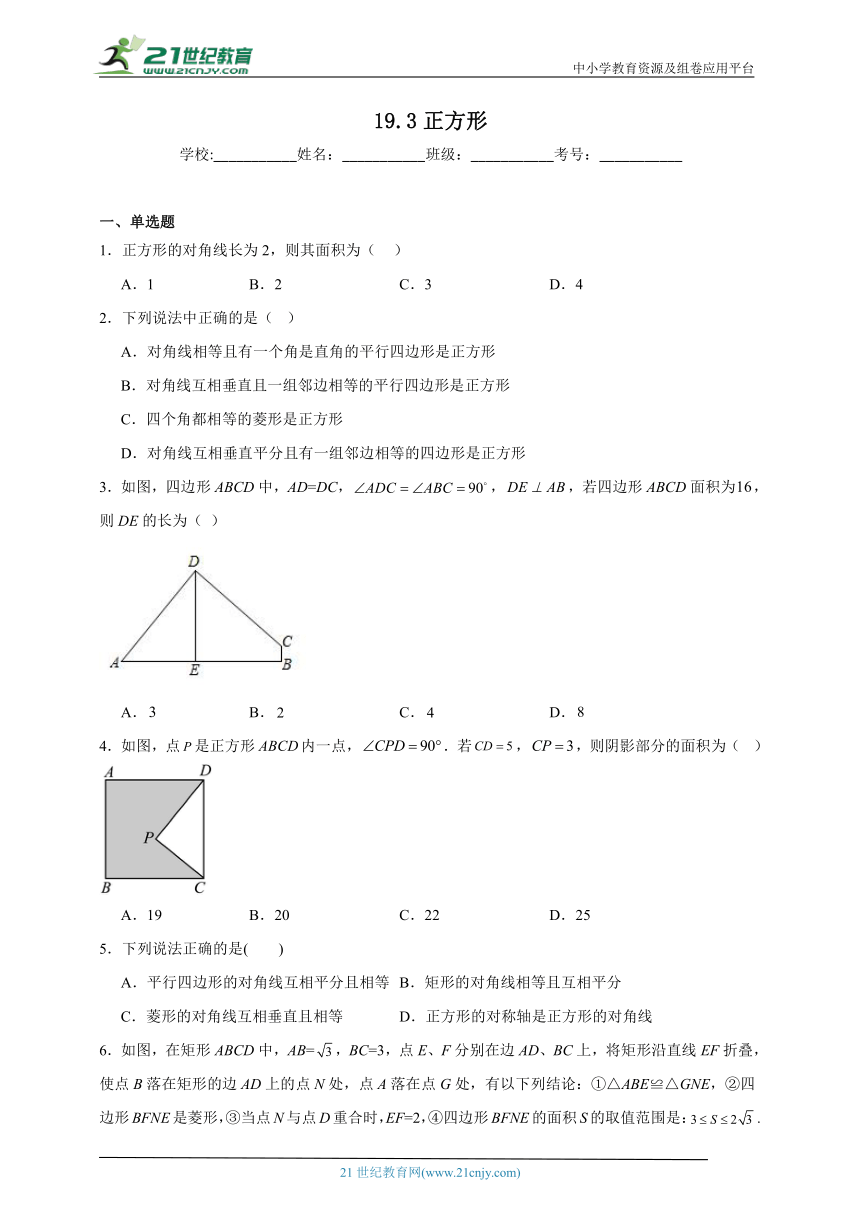
3.如图,四边形ABCD中,AD=DC,,,若四边形ABCD面积为,则DE的长为( )
A. B. C. D.
4.如图,点是正方形内一点,.若,,则阴影部分的面积为( )
A.19 B.20 C.22 D.25
5.下列说法正确的是( )
A.平行四边形的对角线互相平分且相等 B.矩形的对角线相等且互相平分
C.菱形的对角线互相垂直且相等 D.正方形的对称轴是正方形的对角线
6.如图,在矩形ABCD中,AB=,BC=3,点E、F分别在边AD、BC上,将矩形沿直线EF折叠,使点B落在矩形的边AD上的点N处,点A落在点G处,有以下列结论:①△ABE≌△GNE,②四边形BFNE是菱形,③当点N与点D重合时,EF=2,④四边形BFNE的面积S的取值范围是:.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
7.正方形、,按如图所示的方式放置,点、、和点、、分别在直线和轴上,则点的坐标是( )
A. B. C. D.
8.如图,正方形ABCD的边长为4,点M在AB上,且AM=1,N是BD上一动点,则AN+MN的最小值为( )
A.4 B. C.5 D.4
9.如图,是射线上一点,过作轴于点,以为边在其右侧作正方形,过的双曲线交边于点,则的值为( )
A. B. C. D.
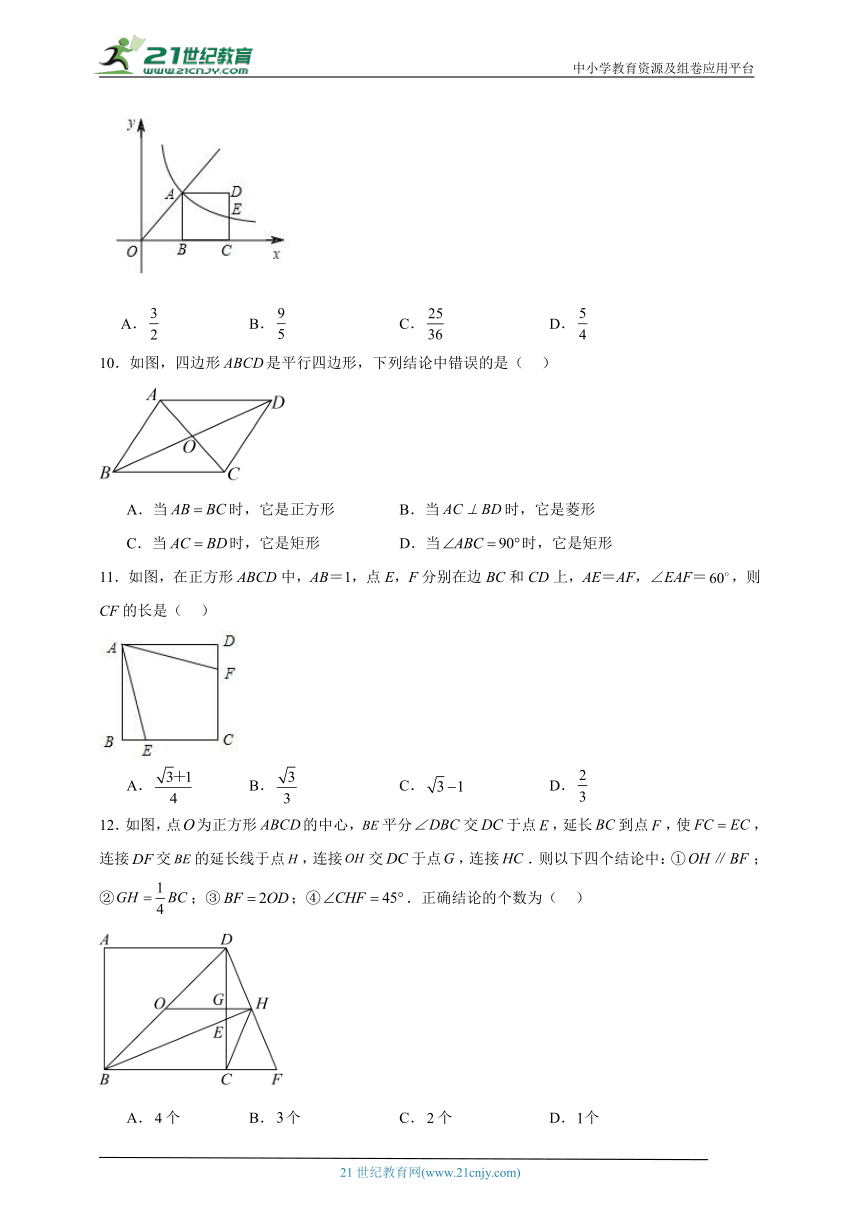
10.如图,四边形是平行四边形,下列结论中错误的是( )
A.当时,它是正方形 B.当时,它是菱形
C.当时,它是矩形 D.当时,它是矩形
11.如图,在正方形ABCD中,AB=1,点E,F分别在边BC和CD上,AE=AF,∠EAF=,则CF的长是( )
A. B. C. D.
12.如图,点为正方形的中心,平分交于点,延长到点,使,连接交的延长线于点,连接交于点,连接.则以下四个结论中:①;②;③;④.正确结论的个数为( )
A.个 B.个 C.个 D.个
二、填空题
13.如图所示的正方形的方格中,∠1+∠3﹣∠2= 度.
14.如图,点E为正方形ABCD外一点,AE=AD,∠ADE=75°,则∠AEB= °.
15.如图.已知反比例与的图象如图所示,点A,B在的图象上,点C,D在的图象上,对角线BD⊥AC于点P,对角线轴.已知点B的横坐标为4:
(1)当m=4,n=20,且P为BD中点,判断四边形ABCD的形状为 .
(2)当四边形ABCD为正方形时m,n之间的数量关系为 .
16.如图,在边长为的正方形中,点为边的中点,点为对角线上一动点,连接、,则周长的最小值为 (结果不取近似值).
17.如图,已知E点在正方形的边的延长线上,且,与相交于点F,则 .
三、解答题
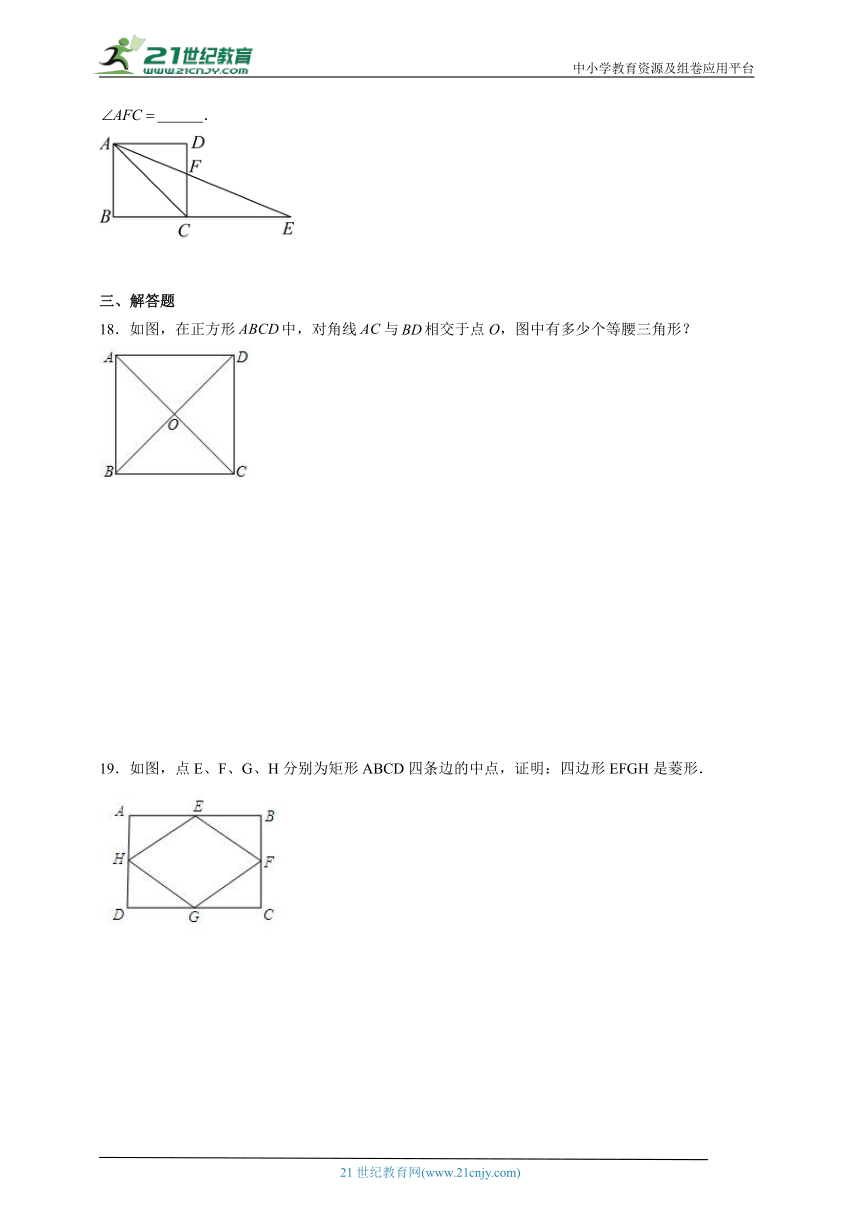
18.如图,在正方形中,对角线与相交于点O,图中有多少个等腰三角形?
19.如图,点E、F、G、H分别为矩形ABCD四条边的中点,证明:四边形EFGH是菱形.
20.如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,你有多少种方法?并与你的同学交流一下.
21.如图所示,在中,,为的中点,四边形为平行四边形,,相交于,连接,.
(1)试确定四边形的形状,并说明理由.
(2)当满足什么条件时,四边形为正方形?请给予证明.
22.(2014四川泸州)如图,正方形ABCD中,E,F分别为BC,CD上的点,且AE⊥BF,垂足为点G,求证:AE=BF.
23.如图,在中,边上的高线长与边的长相等.你能把割补成一个正方形吗?若能,请说明方法及理由.
24.阅读与思考
黄金分割
黄金分割起源于古希腊的毕达哥拉斯学派,公元前4世纪,古希腊数学家欧多克索斯第一个系统研究了黄金分割比例这一问题,并建立起比例理论.后来欧几里得进一步系统论述了黄金分割,其《几何原本》成为最早的有关黄金分割的论著.黄金分割指的是把一条线段分成两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比.
黄金分割在美学、艺术、建筑和日常生活方面有看广泛的应用.如埃及的金字塔、印度的泰姬陵等,都可发现与黄金比有联系的数据.20世纪70年代,这种方法经过我国著名数学家华罗庚的倡导在我国得到大规模推广,取得了很大的成就
如图1的作法是由《几何原本》中给出:
(1)以线段为边作正方形.
(2)取的中点,连接.
(3)在的延长线上取点,使.
(4)以线段为边作正方形.
点就是线段的黄金分割点.
以下是证明点是线段的黄金分割点的部分过程.
证明:设正方形的边长为1,则.
∵点是的中点,∴.
在中,由勾股定理得:.
…
任务:
(1)请根据上面的操作步骤,将上述证明过程补充完整.
(2)如图2,点,是线段的两个黄金分割点,且,则_____,_____.
《19.3正方形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C A B D B C A A
题号 11 12
答案 C B
1.B
【分析】根据正方形是特殊的菱形,所以正方形面积等于对角线乘积的一半即可得出答案.
【详解】解:正方形的对角线长为2,
面积为:
故选B.
【点睛】本题考查了正方形的性质,解决本题的关键是掌握正方形的性质.
2.C
【分析】根据正方形的判定方法即可判断;
【详解】解:A、对角线相等且有一个角是直角的平行四边形是正方形.这个四边形是矩形,不一定是正方形;本选项不符合题意;
B、对角线互相垂直且一组邻边相等的平行四边形是正方形.这个四边形是菱形,不一定是正方形;本选项不符合题意;
C、四个角都相等的菱形是正方形.正确,本选项符合题意;
D、对角线互相垂直平分且有一组邻边相等的四边形是正方形.这个四边形是菱形,不一定是正方形;本选项不符合题意;
故选C.
【点睛】本题考查正方形的判定、平行四边形的性质、菱形的判定、矩形的判定等知识,解题的关键是熟练掌握基本知识.
3.C
【分析】先作BC的垂线,交BC的延长线与F,再证明△ADF≌△CDF,然后可得答案.
【详解】解:过点D作BC的垂线,交BC的延长线与F,
∵,
∴∠A+∠BCD=180°,
∵∠DCF+∠BCD=180°,
∴∠A=∠FCD,
∵,
∴∠AED=∠F=90°,
∵AD=DC,
∴△ADE≌△CDF,
∴DE=DF,
∴四边形ABCD的面积=正方形DEBF=16,
∴DE=4.
故选C
【点睛】本题考查了三角形全等,掌握三角形全等的判定是解决本题的关键.
4.A
【分析】利用勾股定理求出,再根据正方形面积减去三角形面积求出阴影部分的面积.
【详解】解:∵,,,
∴,
∴阴影部分的面积为,
故选:A.
【点睛】此题考查了勾股定理,正方形的性质,熟练掌握勾股定理是解题的关键.
5.B
【分析】根据平行四边形,矩形,菱形,正方形的对角线的性质逐一判断即可.
【详解】A. 平行四边形的对角线互相平分,不一定相等,故该选项错误;
B. 矩形的对角线相等且互相平分,该选项正确;
C. 菱形的对角线互相垂直平分,不一定相等,故该选项错误;
D. 对称轴是一条直线,而正方形的对角线是一条线段,故该选项错误;
故选:B.
【点睛】本题主要考查平行四边形,矩形,菱形,正方形的对角线的性质,掌握平行四边形,矩形,菱形,正方形的对角线的性质是解题的关键.
6.D
【分析】①由矩形的性质,折叠可知:∠A=∠G=90°AB=GN,BE=EN,可以证明Rt△ABE≌Rt△GNE(HL),故①正确;
②由矩形的性质,折叠可知:EN∥BF,BF=FN,所以得到∠NEF=∠BFE,可以证EN=BF,又因为EN∥BF,所以四边形EBFN为平行四边形;又因为BF=NF,即可证明四边形EBFN为菱形;故②正确;
③当点N与点D重合时,如图所示:可得AB=CD= ,BC=3,在Rt BCN中,由勾股定理可得BN ,求出NO=NC=,证明Rt NOF Rt NCF(HL),得到FC=FO,在Rt NFC中,设FC=x,则NF=3-x,由勾股定理可得 ,解得:FC=FO=1,所以EF=2FO=2,故③正确;
④当N和D重合时,菱形BFNE面积最大,S最大= ;当N和A重合时,菱形BFNE面积最小,S最小= ,可以四边形BFNE的面积S的取值范围得④正确;
【详解】①由矩形的性质,折叠可知:∠A=∠G=90°AB=GN,BE=EN
在Rt△ABE和Rt△GNE中,
,
∴Rt△ABE≌Rt△GNE(HL),故①正确;
②由矩形的性质,折叠可知:EN∥BF,BF=FN
∵EN∥BF
∴∠NEF=∠BFE,
又因为∠BFE=∠NFE,
∴∠NEF=∠NFE
∴EN=FN,
∴EN=BF
又因为EN∥BF
∴四边形EBFN为平行四边形;
又因为BF=NF
∴四边形EBFN为菱形;故②正确;
③当点N与点D重合时,如图所示:
AB=CD= ,BC=3,
在Rt BCN中,由勾股定理
BN= ,
,
∴N0=NC= ,
在Rt NOF和Rt NCF中,
∴Rt NOF Rt NCF(HL),
∴FC=FO
在Rt NFC中,设FC=x,则NF=3-x,由勾股定理可得,
∴
解得:x=1
∴FC=FO=1,
∴EF=2FO=2,故③正确;
当N和D重合时,
菱形BFNE面积最大,S最大= ;
当N和A重合时,
菱形BFNE面积最小,S最小= ,
四边形BFNE的面积S的取值范围是:
故④正确;
故正确的序号是:①②③④;
故选:D
【点睛】本题考查了矩形折叠问题,此题是四边形综合题,主要考查了折叠问题与菱形的判定与性质、勾股定理的综合应用,熟练掌握菱形的判定定理和性质定理、勾股定理是解本题的关键;
7.B
【分析】本题考查一次函数图象上点的坐标的特征,正方形的性质,等腰直角三角形的性质,能够找出坐标的变化规律是解题的关键.
分别求出、、、、,探究坐标的变化规律,进而得出的坐标,做出选择即可.
【详解】解:当时,,
当时,,
,是等腰直角三角形,
同理可得:,,都是等腰直角三角形,
于是:,,,,
,
.
故选:.
8.C
【分析】连接AC,则直线AC即为BD的垂直平分线,点A与点C关于直线BD对称,连CM交BD于点N,则此时AN+MN的值最小,连接AN,根据垂直平分线的性质
可得AN=CN,从而得出AN+MN=CN+MN=CM,再根据勾股定理得出CM的长即可解决问题.
【详解】解:在正方形ABCD中连接AC,则点A与点C是关于直线BD为对称轴的对称点,
∴连接MC交BD于点N,则此时AN+MN的值最小,
连接AN,
∵直线AC即为BD的垂直平分线,
∴AN=NC
∴AN+MN=CN+MN=CM,
∵四边形ABCD为正方形,AM=1
∴BC=4,BM=4-1=3,∠CBM=90°,
∴,
∴AN+MN的最小值是5.
故选:C.
【点睛】本题考查了轴对称-最短路线问题,正方形的性质,勾股定理等知识点,此题的难点在于利用轴对称的方法确定满足条件的点N的位置.
9.A
【分析】设点B的坐标为(m,0),则点A的坐标为(m,),把点A的坐标代入反比例函数,得到反比例函数的解析式为y=,结合正方形的性质,得到点C,点D和点E的横坐标,把点E的横坐标代入反比例函数的解析式,得到点E的纵坐标,求出线段DE和线段EC的长度,即可得到答案.
【详解】解:设点B的坐标为(m,0),则点A的坐标为(m,),
∴线段AB的长度为,点D的纵坐标为,
∵点A在反比例函数上,
∴k=,即反比例函数的解析式为:y=,
∵四边形ABCD为正方形,
∴正方形ABCD的边长为,
点C,点D和点E的横坐标为m+,
把x=代入y=得:y=,即点E的纵坐标为,
∴EC=,DE=,
∴,
故选:A.
【点睛】本题考查了一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征和正方形的性质,正确掌握待定系数法和正方形的性质是解题的关键.
10.A
【分析】根据正方形的判定、矩形的判定、菱形的判定逐项判断即可得.
【详解】解:A、当时,它是菱形(有一组邻边相等的平行四边形是菱形),不一定是正方形,则此项错误,符合题意;
B、当时,它是菱形(对角线互相垂直的平行四边形是菱形),则此项正确,不符合题意;
C、当时,它是矩形(对角线相等的平行四边形是矩形),则此项正确,不符合题意;
D、当时,它是矩形(有一个角是直角的平行四边形是矩形),则此项正确,不符合题意;
故选:A.
【点睛】本题考查了正方形的判定、矩形的判定、菱形的判定,熟练掌握特殊四边形的判定是解题关键.
11.C
【分析】由正方形的性质得出∠B=∠D=∠BAD=90°,AB=BC=CD=AD=1,证明Rt△ABE≌Rt△ADF得出∠BAE=∠DAF,求出∠DAF=15°,在AD上取一点G,使∠GFA=∠DAF=15°,则AG=FG,∠DGF=30°,由直角三角形的性质得出DF=FG=AG,DG=DF,设DF=x,则DG=x,AG=FG=2x,则2x+x=1,解得:x=2-,得出DF=2-,即可得出结果.
【详解】解:∵四边形ABCD是正方形,
∴∠B=∠D=∠BAD=90°,AB=BC=CD=AD=1,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴∠BAE=∠DAF,
∵∠EAF=60°,
∴∠BAE+∠DAF=30°,
∴∠DAF=15°,
在AD上取一点G,使∠GFA=∠DAF=15°,如图所示:
∴AG=FG,∠DGF=30°,
∴DF=FG=AG,DG=DF,
设DF=x,则DG=x,AG=FG=2x,
∵AG+DG=AD,
∴2x+x=1,
解得:x=2-,
∴DF=2-,
∴CF=CD-DF=1-(2-)=-1;
故选:C.
【点睛】本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定、直角三角形的性质等知识;熟练掌握正方形的性质,证明三角形全等是解题的关键.
12.B
【分析】本题主要考查正方形的性质、全等三角形的判定及性质、角平分线的定义、三角形的中位线定理,牢记正方形的性质、全等三角形的判定定理及性质、角平分线的定义、三角形的中位线定理是解题的关键.
①先证得,求得,再证得,进而证得,进而证得为的中点,即可判断该说法是否正确.
②根据,,,即可判断该说法是否正确.
③根据,即可判断该说法是否正确.
④由题意可求得,结合三角形的外角的性质,判断该说法是否正确.
【详解】①在和中,
,
∴,
∴,
∵,,
∴,
∴,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
∵为正方形的中心,
∴,
∴,
说法①正确.
②∵为的中位线,
∴,,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
说法②错误.
③∵,
∴,
∵为正方形的中心,
∴,
∴,
说法③正确.
④∵为正方形的中心,
∴,
∵平分,
∴,
∵,
∴,
∵在中,,
∴,
∴,
∴,
说法④正确.
综上所述,说法正确的为①③④,
故选.
13.45
【分析】由网格可知∠1+∠3=90°,∠2=45°,计算即可求解.
【详解】解:由正方形网格可知∠1+∠3=90°,∠2=45°,
∠1+∠3﹣∠2=90°-45°=45°,
故答案为:45.
【点睛】本题考查了网格中的角度问题,解题关键是明确正方形的性质,准确得出角的度数.
14.30
【分析】根据等腰三角形的性质求出,然后求出的度数,再根据等腰三角形两底角相等列式计算即可得解.
【详解】,,
,
,
,
,
.
故答案为:.
【点睛】本题考查了正方形的性质,等腰三角形两底角相等的性质,熟记性质并准确识图是解题的关键.
15. 菱形 m+n=32
【分析】(1)先确定出点B,D坐标,再利用待定系数法即可得出结论,确定出点A,C,P坐标,进而求出PA,PC,即可得出结论;
(2)先确定出,进而求出点P的坐标,再求出A,C坐标,最后用AC=BD,即可得出结论.
【详解】解:(1)∵点B的横坐标为4,
∴当x=4时,,
∴点,
设,则,
∵P为BD中点,
∴PA=PC,
∵轴.
∴点P的横坐标为4,
∴,解得:,
∴,
∴点P(4,3),
∴PB=PD=2,
∴四边形ABCD是平行四边形,
∵BD⊥AC,
∴四边形ABCD是菱形;
故答案为:菱形
(2)∵四边形ABCD为正方形,
∴BD=AC,
当x=4时,,
∴点,
∴,
∴,
∵AC=BD,
∴,
∴m+n=32.
故答案为:m+n=32
【点睛】此题主要考查了反比例函数图象上点的坐标特征,平行四边形的判定,菱形的判定和性质,正方形的性质,判断出四边形ABCD是平行四边形是解本题的关键.
16./
【分析】
本题考查轴对称问题,正方形的性质,勾股定理等等,由于点与点关于对称,所以如果连接,交于点,那么的周长最小,此时的周长.在中,由勾股定理先计算出的长度,再得出结果.
【详解】
连接,交于点,连接、,交于.
四边形是正方形,
,,,
点与点关于对称,
,
.
在中,,
的周长的最小值为:.
故答案为:.
17.
【分析】根据正方形的性质、等腰三角形的性质和三角形的外角的性质,得,然后根据三角形的内角和定理进行计算即可.
【详解】解:∵四边形是正方形,
∴,
∵,
∴,
∵是的外角,
∴,
则,
∴.
故答案为:.
【点睛】本题考查了正方形的性质、三角形的外角、三角形的内角和及等腰三角形,熟练掌握这些知识是解题的关键.
18.图中有8个等腰三角形,并且都是等腰直角三角形.
【分析】分别考虑以正方形的对角线为斜边的等腰三角形和以正方形的边为斜边的等腰三角形即可.
【详解】以正方形的对角线为斜边的等腰三角形共有4个,分别是△ABC,△ADC,△ABD,△BCD,
以正方形的边为斜边的等腰三角形共有4个,分别是△AOB,△BOC,△OCD,△AOD,
故总共有8个等腰三角形,且都是等腰直角三角形.
【点睛】本题考查了正方形的性质、等腰三角形的定义,掌握正方形的性质是关键,另外不要出现遗漏或重复.
19.证明见解析.
【分析】根据矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,利用三角形中位线定理求证EF=FG=GH=EH,然后利用四条边都相等的平行四边形是菱形即可判定.
【详解】解:连接BD,AC.
∵矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
∴AC=BD,
∴EF=AC,GH=AC,
同理,FG=BD,EH=BD
∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
20.有无数种分法
【分析】根据正方形的性质画图即可,只要两条小路过正方形草地的两条对角线交点且互相垂直即可;第一张图:以正方形的对角线为依据作图;第二张图:以正方形边的平分线为依据作图.
【详解】过正方形的中心引两条互相垂直的直线,即可将正方形分成四部分相等的面积,所以方法有无数种,如图为两种划分方法.
【点睛】题目主要考查正方形的性质,熟练掌握并灵活运用是解题关键.
21.(1)四边形是矩形,理由见解析
(2),证明见解析
【分析】(1)由等腰三角形的三线合一得,,从而,再根据四边形的性质得,,从而证明,,四边形是平行四边形,根据得是矩形;
(2)当时,根据平行线的性质证明即可得矩形为正方形.
【详解】(1)解:四边形是矩形理由如下,
∵,为的中点,
,,
∴,
∵四边形为平行四边形,
.,,
,,
∴四边形是平行四边形,
又∵,
∴是矩形;
(2)解:当时,四边形为正方形,
证明:∵四边形为平行四边形,
,
∴,
∵,
∴,
∴,
∴矩形为正方形.
22.见解析
【详解】证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCF=90°,∴∠BAE+∠AEB=90°.
又∵AE⊥BF,垂足为G,∴∠CBF+∠AEB=90°.
∴∠BAE=∠CBF.
在△ABE与△BCF中,
∴△ABE≌△BCF(ASA),
∴AE=BF.
23.能,方法和理由见解析
【分析】过点作于,把沿着平移到,可得四边形是正方形;再根据正方形的判定定理进行证明即可.
【详解】
过点作于,
把沿着平移到,
则四边形是正方形;
理由如下:
∵四边形是平行四边形,
∴,
,
,
,
∴四边形是矩形,
在中,边上的高线长与边的长相等,
∴,
∴四边形是正方形.
【点睛】本题考查了平行四边形的性质,正方形的判定定理,平移的性质,能够正确作图是解题的关键.
24.(1)见解析;(2)4,.
【分析】(1)由图形可知,,即可求证.即证明点是线段的黄金分割点.
(2)根据(1)可得,又由题意,即可求出的长,最后由即可求出BC长.
【详解】(1)证明:设正方形的边长为1,则.
∵点是的中点,
∴.
在中,由勾股定理得:,
则,
∴,
∴,,
即.
故点是线段的黄金分割点.
(2)解:∵点是的黄金分割点,
根据(1)可得,解得,
则.
故答案为4,.
【点睛】本题考查正方形的性质,勾股定理以及理解黄金分割的定义.解题的关键是正确理解题意,明确黄金分割的意义.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
19.3正方形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.正方形的对角线长为2,则其面积为( )
A.1 B.2 C.3 D.4
2.下列说法中正确的是( )
A.对角线相等且有一个角是直角的平行四边形是正方形
B.对角线互相垂直且一组邻边相等的平行四边形是正方形
C.四个角都相等的菱形是正方形
D.对角线互相垂直平分且有一组邻边相等的四边形是正方形
3.如图,四边形ABCD中,AD=DC,,,若四边形ABCD面积为,则DE的长为( )
A. B. C. D.
4.如图,点是正方形内一点,.若,,则阴影部分的面积为( )
A.19 B.20 C.22 D.25
5.下列说法正确的是( )
A.平行四边形的对角线互相平分且相等 B.矩形的对角线相等且互相平分
C.菱形的对角线互相垂直且相等 D.正方形的对称轴是正方形的对角线
6.如图,在矩形ABCD中,AB=,BC=3,点E、F分别在边AD、BC上,将矩形沿直线EF折叠,使点B落在矩形的边AD上的点N处,点A落在点G处,有以下列结论:①△ABE≌△GNE,②四边形BFNE是菱形,③当点N与点D重合时,EF=2,④四边形BFNE的面积S的取值范围是:.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
7.正方形、,按如图所示的方式放置,点、、和点、、分别在直线和轴上,则点的坐标是( )
A. B. C. D.
8.如图,正方形ABCD的边长为4,点M在AB上,且AM=1,N是BD上一动点,则AN+MN的最小值为( )
A.4 B. C.5 D.4
9.如图,是射线上一点,过作轴于点,以为边在其右侧作正方形,过的双曲线交边于点,则的值为( )
A. B. C. D.
10.如图,四边形是平行四边形,下列结论中错误的是( )
A.当时,它是正方形 B.当时,它是菱形
C.当时,它是矩形 D.当时,它是矩形
11.如图,在正方形ABCD中,AB=1,点E,F分别在边BC和CD上,AE=AF,∠EAF=,则CF的长是( )
A. B. C. D.
12.如图,点为正方形的中心,平分交于点,延长到点,使,连接交的延长线于点,连接交于点,连接.则以下四个结论中:①;②;③;④.正确结论的个数为( )
A.个 B.个 C.个 D.个
二、填空题
13.如图所示的正方形的方格中,∠1+∠3﹣∠2= 度.
14.如图,点E为正方形ABCD外一点,AE=AD,∠ADE=75°,则∠AEB= °.
15.如图.已知反比例与的图象如图所示,点A,B在的图象上,点C,D在的图象上,对角线BD⊥AC于点P,对角线轴.已知点B的横坐标为4:
(1)当m=4,n=20,且P为BD中点,判断四边形ABCD的形状为 .
(2)当四边形ABCD为正方形时m,n之间的数量关系为 .
16.如图,在边长为的正方形中,点为边的中点,点为对角线上一动点,连接、,则周长的最小值为 (结果不取近似值).
17.如图,已知E点在正方形的边的延长线上,且,与相交于点F,则 .
三、解答题
18.如图,在正方形中,对角线与相交于点O,图中有多少个等腰三角形?
19.如图,点E、F、G、H分别为矩形ABCD四条边的中点,证明:四边形EFGH是菱形.
20.如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,你有多少种方法?并与你的同学交流一下.
21.如图所示,在中,,为的中点,四边形为平行四边形,,相交于,连接,.
(1)试确定四边形的形状,并说明理由.
(2)当满足什么条件时,四边形为正方形?请给予证明.
22.(2014四川泸州)如图,正方形ABCD中,E,F分别为BC,CD上的点,且AE⊥BF,垂足为点G,求证:AE=BF.
23.如图,在中,边上的高线长与边的长相等.你能把割补成一个正方形吗?若能,请说明方法及理由.
24.阅读与思考
黄金分割
黄金分割起源于古希腊的毕达哥拉斯学派,公元前4世纪,古希腊数学家欧多克索斯第一个系统研究了黄金分割比例这一问题,并建立起比例理论.后来欧几里得进一步系统论述了黄金分割,其《几何原本》成为最早的有关黄金分割的论著.黄金分割指的是把一条线段分成两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比.
黄金分割在美学、艺术、建筑和日常生活方面有看广泛的应用.如埃及的金字塔、印度的泰姬陵等,都可发现与黄金比有联系的数据.20世纪70年代,这种方法经过我国著名数学家华罗庚的倡导在我国得到大规模推广,取得了很大的成就
如图1的作法是由《几何原本》中给出:
(1)以线段为边作正方形.
(2)取的中点,连接.
(3)在的延长线上取点,使.
(4)以线段为边作正方形.
点就是线段的黄金分割点.
以下是证明点是线段的黄金分割点的部分过程.
证明:设正方形的边长为1,则.
∵点是的中点,∴.
在中,由勾股定理得:.
…
任务:
(1)请根据上面的操作步骤,将上述证明过程补充完整.
(2)如图2,点,是线段的两个黄金分割点,且,则_____,_____.
《19.3正方形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C A B D B C A A
题号 11 12
答案 C B
1.B
【分析】根据正方形是特殊的菱形,所以正方形面积等于对角线乘积的一半即可得出答案.
【详解】解:正方形的对角线长为2,
面积为:
故选B.
【点睛】本题考查了正方形的性质,解决本题的关键是掌握正方形的性质.
2.C
【分析】根据正方形的判定方法即可判断;
【详解】解:A、对角线相等且有一个角是直角的平行四边形是正方形.这个四边形是矩形,不一定是正方形;本选项不符合题意;
B、对角线互相垂直且一组邻边相等的平行四边形是正方形.这个四边形是菱形,不一定是正方形;本选项不符合题意;
C、四个角都相等的菱形是正方形.正确,本选项符合题意;
D、对角线互相垂直平分且有一组邻边相等的四边形是正方形.这个四边形是菱形,不一定是正方形;本选项不符合题意;
故选C.
【点睛】本题考查正方形的判定、平行四边形的性质、菱形的判定、矩形的判定等知识,解题的关键是熟练掌握基本知识.
3.C
【分析】先作BC的垂线,交BC的延长线与F,再证明△ADF≌△CDF,然后可得答案.
【详解】解:过点D作BC的垂线,交BC的延长线与F,
∵,
∴∠A+∠BCD=180°,
∵∠DCF+∠BCD=180°,
∴∠A=∠FCD,
∵,
∴∠AED=∠F=90°,
∵AD=DC,
∴△ADE≌△CDF,
∴DE=DF,
∴四边形ABCD的面积=正方形DEBF=16,
∴DE=4.
故选C
【点睛】本题考查了三角形全等,掌握三角形全等的判定是解决本题的关键.
4.A
【分析】利用勾股定理求出,再根据正方形面积减去三角形面积求出阴影部分的面积.
【详解】解:∵,,,
∴,
∴阴影部分的面积为,
故选:A.
【点睛】此题考查了勾股定理,正方形的性质,熟练掌握勾股定理是解题的关键.
5.B
【分析】根据平行四边形,矩形,菱形,正方形的对角线的性质逐一判断即可.
【详解】A. 平行四边形的对角线互相平分,不一定相等,故该选项错误;
B. 矩形的对角线相等且互相平分,该选项正确;
C. 菱形的对角线互相垂直平分,不一定相等,故该选项错误;
D. 对称轴是一条直线,而正方形的对角线是一条线段,故该选项错误;
故选:B.
【点睛】本题主要考查平行四边形,矩形,菱形,正方形的对角线的性质,掌握平行四边形,矩形,菱形,正方形的对角线的性质是解题的关键.
6.D
【分析】①由矩形的性质,折叠可知:∠A=∠G=90°AB=GN,BE=EN,可以证明Rt△ABE≌Rt△GNE(HL),故①正确;
②由矩形的性质,折叠可知:EN∥BF,BF=FN,所以得到∠NEF=∠BFE,可以证EN=BF,又因为EN∥BF,所以四边形EBFN为平行四边形;又因为BF=NF,即可证明四边形EBFN为菱形;故②正确;
③当点N与点D重合时,如图所示:可得AB=CD= ,BC=3,在Rt BCN中,由勾股定理可得BN ,求出NO=NC=,证明Rt NOF Rt NCF(HL),得到FC=FO,在Rt NFC中,设FC=x,则NF=3-x,由勾股定理可得 ,解得:FC=FO=1,所以EF=2FO=2,故③正确;
④当N和D重合时,菱形BFNE面积最大,S最大= ;当N和A重合时,菱形BFNE面积最小,S最小= ,可以四边形BFNE的面积S的取值范围得④正确;
【详解】①由矩形的性质,折叠可知:∠A=∠G=90°AB=GN,BE=EN
在Rt△ABE和Rt△GNE中,
,
∴Rt△ABE≌Rt△GNE(HL),故①正确;
②由矩形的性质,折叠可知:EN∥BF,BF=FN
∵EN∥BF
∴∠NEF=∠BFE,
又因为∠BFE=∠NFE,
∴∠NEF=∠NFE
∴EN=FN,
∴EN=BF
又因为EN∥BF
∴四边形EBFN为平行四边形;
又因为BF=NF
∴四边形EBFN为菱形;故②正确;
③当点N与点D重合时,如图所示:
AB=CD= ,BC=3,
在Rt BCN中,由勾股定理
BN= ,
,
∴N0=NC= ,
在Rt NOF和Rt NCF中,
∴Rt NOF Rt NCF(HL),
∴FC=FO
在Rt NFC中,设FC=x,则NF=3-x,由勾股定理可得,
∴
解得:x=1
∴FC=FO=1,
∴EF=2FO=2,故③正确;
当N和D重合时,
菱形BFNE面积最大,S最大= ;
当N和A重合时,
菱形BFNE面积最小,S最小= ,
四边形BFNE的面积S的取值范围是:
故④正确;
故正确的序号是:①②③④;
故选:D
【点睛】本题考查了矩形折叠问题,此题是四边形综合题,主要考查了折叠问题与菱形的判定与性质、勾股定理的综合应用,熟练掌握菱形的判定定理和性质定理、勾股定理是解本题的关键;
7.B
【分析】本题考查一次函数图象上点的坐标的特征,正方形的性质,等腰直角三角形的性质,能够找出坐标的变化规律是解题的关键.
分别求出、、、、,探究坐标的变化规律,进而得出的坐标,做出选择即可.
【详解】解:当时,,
当时,,
,是等腰直角三角形,
同理可得:,,都是等腰直角三角形,
于是:,,,,
,
.
故选:.
8.C
【分析】连接AC,则直线AC即为BD的垂直平分线,点A与点C关于直线BD对称,连CM交BD于点N,则此时AN+MN的值最小,连接AN,根据垂直平分线的性质
可得AN=CN,从而得出AN+MN=CN+MN=CM,再根据勾股定理得出CM的长即可解决问题.
【详解】解:在正方形ABCD中连接AC,则点A与点C是关于直线BD为对称轴的对称点,
∴连接MC交BD于点N,则此时AN+MN的值最小,
连接AN,
∵直线AC即为BD的垂直平分线,
∴AN=NC
∴AN+MN=CN+MN=CM,
∵四边形ABCD为正方形,AM=1
∴BC=4,BM=4-1=3,∠CBM=90°,
∴,
∴AN+MN的最小值是5.
故选:C.
【点睛】本题考查了轴对称-最短路线问题,正方形的性质,勾股定理等知识点,此题的难点在于利用轴对称的方法确定满足条件的点N的位置.
9.A
【分析】设点B的坐标为(m,0),则点A的坐标为(m,),把点A的坐标代入反比例函数,得到反比例函数的解析式为y=,结合正方形的性质,得到点C,点D和点E的横坐标,把点E的横坐标代入反比例函数的解析式,得到点E的纵坐标,求出线段DE和线段EC的长度,即可得到答案.
【详解】解:设点B的坐标为(m,0),则点A的坐标为(m,),
∴线段AB的长度为,点D的纵坐标为,
∵点A在反比例函数上,
∴k=,即反比例函数的解析式为:y=,
∵四边形ABCD为正方形,
∴正方形ABCD的边长为,
点C,点D和点E的横坐标为m+,
把x=代入y=得:y=,即点E的纵坐标为,
∴EC=,DE=,
∴,
故选:A.
【点睛】本题考查了一次函数图象上点的坐标特征,反比例函数图象上点的坐标特征和正方形的性质,正确掌握待定系数法和正方形的性质是解题的关键.
10.A
【分析】根据正方形的判定、矩形的判定、菱形的判定逐项判断即可得.
【详解】解:A、当时,它是菱形(有一组邻边相等的平行四边形是菱形),不一定是正方形,则此项错误,符合题意;
B、当时,它是菱形(对角线互相垂直的平行四边形是菱形),则此项正确,不符合题意;
C、当时,它是矩形(对角线相等的平行四边形是矩形),则此项正确,不符合题意;
D、当时,它是矩形(有一个角是直角的平行四边形是矩形),则此项正确,不符合题意;
故选:A.
【点睛】本题考查了正方形的判定、矩形的判定、菱形的判定,熟练掌握特殊四边形的判定是解题关键.
11.C
【分析】由正方形的性质得出∠B=∠D=∠BAD=90°,AB=BC=CD=AD=1,证明Rt△ABE≌Rt△ADF得出∠BAE=∠DAF,求出∠DAF=15°,在AD上取一点G,使∠GFA=∠DAF=15°,则AG=FG,∠DGF=30°,由直角三角形的性质得出DF=FG=AG,DG=DF,设DF=x,则DG=x,AG=FG=2x,则2x+x=1,解得:x=2-,得出DF=2-,即可得出结果.
【详解】解:∵四边形ABCD是正方形,
∴∠B=∠D=∠BAD=90°,AB=BC=CD=AD=1,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴∠BAE=∠DAF,
∵∠EAF=60°,
∴∠BAE+∠DAF=30°,
∴∠DAF=15°,
在AD上取一点G,使∠GFA=∠DAF=15°,如图所示:
∴AG=FG,∠DGF=30°,
∴DF=FG=AG,DG=DF,
设DF=x,则DG=x,AG=FG=2x,
∵AG+DG=AD,
∴2x+x=1,
解得:x=2-,
∴DF=2-,
∴CF=CD-DF=1-(2-)=-1;
故选:C.
【点睛】本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定、直角三角形的性质等知识;熟练掌握正方形的性质,证明三角形全等是解题的关键.
12.B
【分析】本题主要考查正方形的性质、全等三角形的判定及性质、角平分线的定义、三角形的中位线定理,牢记正方形的性质、全等三角形的判定定理及性质、角平分线的定义、三角形的中位线定理是解题的关键.
①先证得,求得,再证得,进而证得,进而证得为的中点,即可判断该说法是否正确.
②根据,,,即可判断该说法是否正确.
③根据,即可判断该说法是否正确.
④由题意可求得,结合三角形的外角的性质,判断该说法是否正确.
【详解】①在和中,
,
∴,
∴,
∵,,
∴,
∴,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
∵为正方形的中心,
∴,
∴,
说法①正确.
②∵为的中位线,
∴,,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
说法②错误.
③∵,
∴,
∵为正方形的中心,
∴,
∴,
说法③正确.
④∵为正方形的中心,
∴,
∵平分,
∴,
∵,
∴,
∵在中,,
∴,
∴,
∴,
说法④正确.
综上所述,说法正确的为①③④,
故选.
13.45
【分析】由网格可知∠1+∠3=90°,∠2=45°,计算即可求解.
【详解】解:由正方形网格可知∠1+∠3=90°,∠2=45°,
∠1+∠3﹣∠2=90°-45°=45°,
故答案为:45.
【点睛】本题考查了网格中的角度问题,解题关键是明确正方形的性质,准确得出角的度数.
14.30
【分析】根据等腰三角形的性质求出,然后求出的度数,再根据等腰三角形两底角相等列式计算即可得解.
【详解】,,
,
,
,
,
.
故答案为:.
【点睛】本题考查了正方形的性质,等腰三角形两底角相等的性质,熟记性质并准确识图是解题的关键.
15. 菱形 m+n=32
【分析】(1)先确定出点B,D坐标,再利用待定系数法即可得出结论,确定出点A,C,P坐标,进而求出PA,PC,即可得出结论;
(2)先确定出,进而求出点P的坐标,再求出A,C坐标,最后用AC=BD,即可得出结论.
【详解】解:(1)∵点B的横坐标为4,
∴当x=4时,,
∴点,
设,则,
∵P为BD中点,
∴PA=PC,
∵轴.
∴点P的横坐标为4,
∴,解得:,
∴,
∴点P(4,3),
∴PB=PD=2,
∴四边形ABCD是平行四边形,
∵BD⊥AC,
∴四边形ABCD是菱形;
故答案为:菱形
(2)∵四边形ABCD为正方形,
∴BD=AC,
当x=4时,,
∴点,
∴,
∴,
∵AC=BD,
∴,
∴m+n=32.
故答案为:m+n=32
【点睛】此题主要考查了反比例函数图象上点的坐标特征,平行四边形的判定,菱形的判定和性质,正方形的性质,判断出四边形ABCD是平行四边形是解本题的关键.
16./
【分析】
本题考查轴对称问题,正方形的性质,勾股定理等等,由于点与点关于对称,所以如果连接,交于点,那么的周长最小,此时的周长.在中,由勾股定理先计算出的长度,再得出结果.
【详解】
连接,交于点,连接、,交于.
四边形是正方形,
,,,
点与点关于对称,
,
.
在中,,
的周长的最小值为:.
故答案为:.
17.
【分析】根据正方形的性质、等腰三角形的性质和三角形的外角的性质,得,然后根据三角形的内角和定理进行计算即可.
【详解】解:∵四边形是正方形,
∴,
∵,
∴,
∵是的外角,
∴,
则,
∴.
故答案为:.
【点睛】本题考查了正方形的性质、三角形的外角、三角形的内角和及等腰三角形,熟练掌握这些知识是解题的关键.
18.图中有8个等腰三角形,并且都是等腰直角三角形.
【分析】分别考虑以正方形的对角线为斜边的等腰三角形和以正方形的边为斜边的等腰三角形即可.
【详解】以正方形的对角线为斜边的等腰三角形共有4个,分别是△ABC,△ADC,△ABD,△BCD,
以正方形的边为斜边的等腰三角形共有4个,分别是△AOB,△BOC,△OCD,△AOD,
故总共有8个等腰三角形,且都是等腰直角三角形.
【点睛】本题考查了正方形的性质、等腰三角形的定义,掌握正方形的性质是关键,另外不要出现遗漏或重复.
19.证明见解析.
【分析】根据矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,利用三角形中位线定理求证EF=FG=GH=EH,然后利用四条边都相等的平行四边形是菱形即可判定.
【详解】解:连接BD,AC.
∵矩形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,
∴AC=BD,
∴EF=AC,GH=AC,
同理,FG=BD,EH=BD
∴EF=FG=GH=EH,
∴四边形EFGH是菱形.
20.有无数种分法
【分析】根据正方形的性质画图即可,只要两条小路过正方形草地的两条对角线交点且互相垂直即可;第一张图:以正方形的对角线为依据作图;第二张图:以正方形边的平分线为依据作图.
【详解】过正方形的中心引两条互相垂直的直线,即可将正方形分成四部分相等的面积,所以方法有无数种,如图为两种划分方法.
【点睛】题目主要考查正方形的性质,熟练掌握并灵活运用是解题关键.
21.(1)四边形是矩形,理由见解析
(2),证明见解析
【分析】(1)由等腰三角形的三线合一得,,从而,再根据四边形的性质得,,从而证明,,四边形是平行四边形,根据得是矩形;
(2)当时,根据平行线的性质证明即可得矩形为正方形.
【详解】(1)解:四边形是矩形理由如下,
∵,为的中点,
,,
∴,
∵四边形为平行四边形,
.,,
,,
∴四边形是平行四边形,
又∵,
∴是矩形;
(2)解:当时,四边形为正方形,
证明:∵四边形为平行四边形,
,
∴,
∵,
∴,
∴,
∴矩形为正方形.
22.见解析
【详解】证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCF=90°,∴∠BAE+∠AEB=90°.
又∵AE⊥BF,垂足为G,∴∠CBF+∠AEB=90°.
∴∠BAE=∠CBF.
在△ABE与△BCF中,
∴△ABE≌△BCF(ASA),
∴AE=BF.
23.能,方法和理由见解析
【分析】过点作于,把沿着平移到,可得四边形是正方形;再根据正方形的判定定理进行证明即可.
【详解】
过点作于,
把沿着平移到,
则四边形是正方形;
理由如下:
∵四边形是平行四边形,
∴,
,
,
,
∴四边形是矩形,
在中,边上的高线长与边的长相等,
∴,
∴四边形是正方形.
【点睛】本题考查了平行四边形的性质,正方形的判定定理,平移的性质,能够正确作图是解题的关键.
24.(1)见解析;(2)4,.
【分析】(1)由图形可知,,即可求证.即证明点是线段的黄金分割点.
(2)根据(1)可得,又由题意,即可求出的长,最后由即可求出BC长.
【详解】(1)证明:设正方形的边长为1,则.
∵点是的中点,
∴.
在中,由勾股定理得:,
则,
∴,
∴,,
即.
故点是线段的黄金分割点.
(2)解:∵点是的黄金分割点,
根据(1)可得,解得,
则.
故答案为4,.
【点睛】本题考查正方形的性质,勾股定理以及理解黄金分割的定义.解题的关键是正确理解题意,明确黄金分割的意义.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
