沪科版(2024)七年级数学下册课件 10.2 第4课时 平行线的判定方法2、3(共19张PPT)
文档属性
| 名称 | 沪科版(2024)七年级数学下册课件 10.2 第4课时 平行线的判定方法2、3(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 938.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 15:00:48 | ||
图片预览




文档简介
(共19张PPT)
10.2 平行线的判定
第四课时 平行线的判定方法2、3
学习目标及重难点
1.掌握平行线的判定方法2,3,并利用所学知识进行简单推理.
2.通过动手操作、发现、探索平行线的判定方法,能灵活地利用平行线的三个判定定理解决问题.
3.主动参与数学活动,主动地进行数学学习,发展应用数学的意识与能力、增强学好数学的愿望和信心.
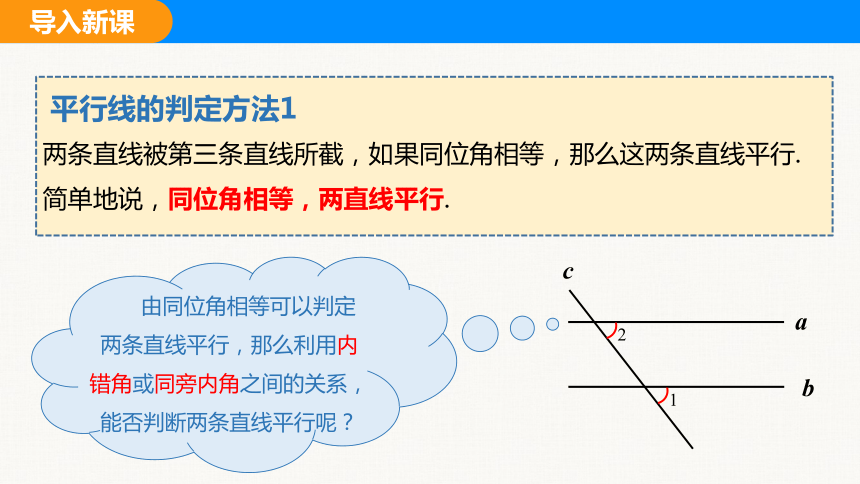
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
平行线的判定方法1
2
1
a
c
b
由同位角相等可以判定两条直线平行,那么利用内错角或同旁内角之间的关系,能否判断两条直线平行呢?
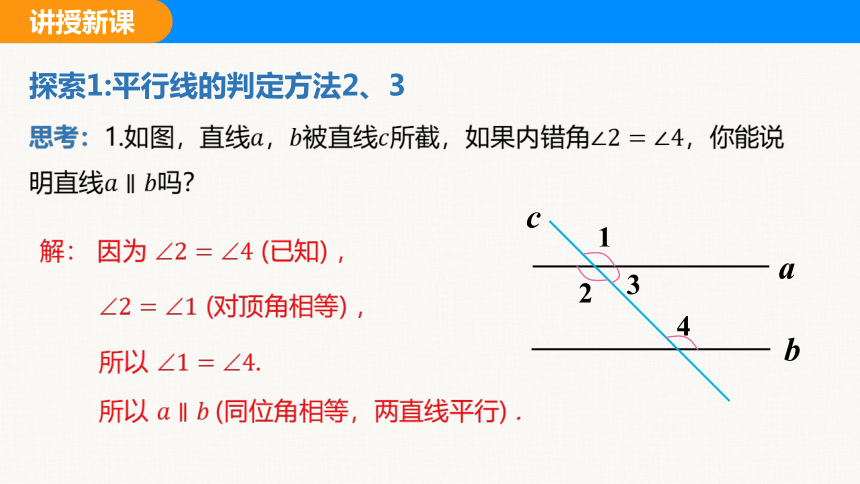
思考:1.如图,直线被直线所截,如果内错角,你能说明直线吗?
b
a
c
3
4
2
1
探索1:平行线的判定方法2、3
解: 因为 (已知) ,
(对顶角相等) ,
所以 .
所以 (同位角相等,两直线平行) .
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
符号语言:
因为(已知),
所以(内错角相等,两直线平行).
平行线的判定方法2
b
a
c
2
1
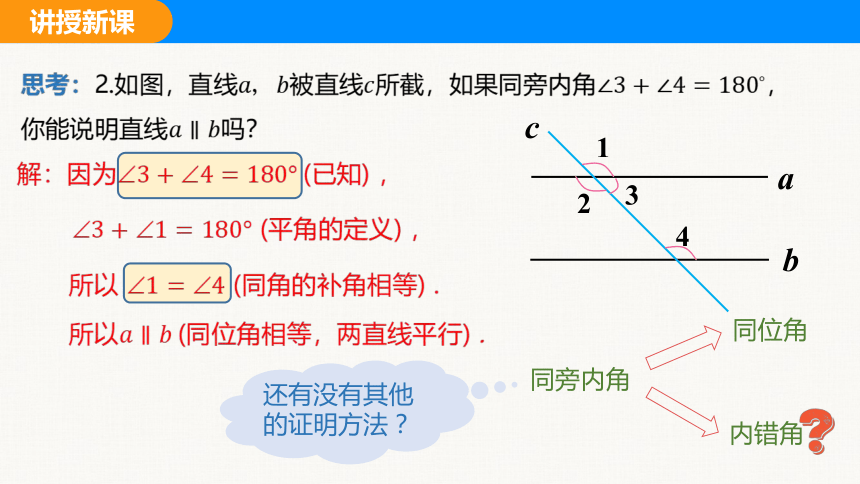
思考:2.如图,直线被直线所截,如果同旁内角,你能说明直线吗?
b
a
c
3
4
2
1
解:因为(已知) ,
(平角的定义) ,
所以 (同角的补角相等) .
所以(同位角相等,两直线平行) .
同旁内角
同位角
内错角
还有没有其他的证明方法?
思考:如图,直线被直线所截,如果同旁内角,你能说明直线吗?
b
a
c
3
4
2
1
解:因为 (已知) ,
(平角的定义) ,
所以(同角的补角相等) .
所以 (内错角相等,两直线平行) .
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
符号语言:
因为(已知),
所以(同旁内角互补,两直线平行).
平行线的判定方法3
b
a
c
1
2
遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.
判定方法1
同位角相等,两直线平行.
判定方法2
内错角相等,两直线平行.
判定方法3
同旁内角互补,两直线平行.
转化
转化
转化
证明
证明
证明
归纳总结
文字简述 符号语言 图示
同位角相等,两直线平行 因为____________(已知),所以
内错角相等,两直线平行 因为____________(已知),所以 同旁内角互补,两直线平行 因为______________(已知),所以 ∠1=∠4
∠2=∠4
∠3+∠4=180°
b
a
c
3
4
2
1
归纳总结
如图,下列推理中正确的是________.(填序号)
①因为,所以;
②因为,所以;
③因为,所以;
④因为,所以
①②④
随堂小练习
例1:如图,已知平分你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
理由:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD( 内错角相等,两直线平行)
∴ AB∥MN(内错角相等,两直线平行)
解:
∵ ∠MCA= ∠ A(已知)
又 ∵∠ DEC= ∠ B(已知)
∴ AB∥DE(同位角相等,两直线平行)
∴ DE∥MN(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
例2:如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,那么DE∥MN吗?为什么?
A
E
B
C
D
N
M
1.根据图所示,明明写出了以下四个条件,其中能判定的是( )
A. B.
C. D.
D
习题1
2.如图所示,一个合格的弯形管道要求现测得,若这个管道符合要求,则的度数为( )
A.25° B.45°
C.55° D.65°
B
习题2
3.如图所示,过点画直线的平行线的作法依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
D
习题3
4.如图所示,已知直线,垂足为,且,则当= °时,
50
习题4
5.如图所示,那么与平行吗 与呢 为什么
解:
理由:因为,
所以
又因为,
所以,
所以
因为,
所以
又因为,
所以
所以.
习题5
平行线的判定方法
定义法:在同一平面内,不相交的两条直线叫作平行线.
平行线基本事实的推论:如果直线,那么直线
判定方法1:同位角相等,两直线平行
判定方法2:内错角相等,两直线平行
判定方法3:同旁内角互补,两直线平行
在同一平面内,垂直于同一条直线的两条直线平行
10.2 平行线的判定
第四课时 平行线的判定方法2、3
学习目标及重难点
1.掌握平行线的判定方法2,3,并利用所学知识进行简单推理.
2.通过动手操作、发现、探索平行线的判定方法,能灵活地利用平行线的三个判定定理解决问题.
3.主动参与数学活动,主动地进行数学学习,发展应用数学的意识与能力、增强学好数学的愿望和信心.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
平行线的判定方法1
2
1
a
c
b
由同位角相等可以判定两条直线平行,那么利用内错角或同旁内角之间的关系,能否判断两条直线平行呢?
思考:1.如图,直线被直线所截,如果内错角,你能说明直线吗?
b
a
c
3
4
2
1
探索1:平行线的判定方法2、3
解: 因为 (已知) ,
(对顶角相等) ,
所以 .
所以 (同位角相等,两直线平行) .
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
符号语言:
因为(已知),
所以(内错角相等,两直线平行).
平行线的判定方法2
b
a
c
2
1
思考:2.如图,直线被直线所截,如果同旁内角,你能说明直线吗?
b
a
c
3
4
2
1
解:因为(已知) ,
(平角的定义) ,
所以 (同角的补角相等) .
所以(同位角相等,两直线平行) .
同旁内角
同位角
内错角
还有没有其他的证明方法?
思考:如图,直线被直线所截,如果同旁内角,你能说明直线吗?
b
a
c
3
4
2
1
解:因为 (已知) ,
(平角的定义) ,
所以(同角的补角相等) .
所以 (内错角相等,两直线平行) .
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
符号语言:
因为(已知),
所以(同旁内角互补,两直线平行).
平行线的判定方法3
b
a
c
1
2
遇到一个新问题时,常常把它转化为已知的(或已解决的)问题.
判定方法1
同位角相等,两直线平行.
判定方法2
内错角相等,两直线平行.
判定方法3
同旁内角互补,两直线平行.
转化
转化
转化
证明
证明
证明
归纳总结
文字简述 符号语言 图示
同位角相等,两直线平行 因为____________(已知),所以
内错角相等,两直线平行 因为____________(已知),所以 同旁内角互补,两直线平行 因为______________(已知),所以 ∠1=∠4
∠2=∠4
∠3+∠4=180°
b
a
c
3
4
2
1
归纳总结
如图,下列推理中正确的是________.(填序号)
①因为,所以;
②因为,所以;
③因为,所以;
④因为,所以
①②④
随堂小练习
例1:如图,已知平分你能判断哪两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
解: AB∥CD.
理由:
∵ AC平分∠DAB(已知)
∴ ∠1=∠2(角平分线定义)
又∵ ∠1= ∠3(已知)
∴ ∠2=∠3(等量代换)
∴ AB∥CD( 内错角相等,两直线平行)
∴ AB∥MN(内错角相等,两直线平行)
解:
∵ ∠MCA= ∠ A(已知)
又 ∵∠ DEC= ∠ B(已知)
∴ AB∥DE(同位角相等,两直线平行)
∴ DE∥MN(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
例2:如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,那么DE∥MN吗?为什么?
A
E
B
C
D
N
M
1.根据图所示,明明写出了以下四个条件,其中能判定的是( )
A. B.
C. D.
D
习题1
2.如图所示,一个合格的弯形管道要求现测得,若这个管道符合要求,则的度数为( )
A.25° B.45°
C.55° D.65°
B
习题2
3.如图所示,过点画直线的平行线的作法依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
D
习题3
4.如图所示,已知直线,垂足为,且,则当= °时,
50
习题4
5.如图所示,那么与平行吗 与呢 为什么
解:
理由:因为,
所以
又因为,
所以,
所以
因为,
所以
又因为,
所以
所以.
习题5
平行线的判定方法
定义法:在同一平面内,不相交的两条直线叫作平行线.
平行线基本事实的推论:如果直线,那么直线
判定方法1:同位角相等,两直线平行
判定方法2:内错角相等,两直线平行
判定方法3:同旁内角互补,两直线平行
在同一平面内,垂直于同一条直线的两条直线平行
