沪科版(2024)七年级数学下册课件 10.3 平行线的性质(共30张PPT)
文档属性
| 名称 | 沪科版(2024)七年级数学下册课件 10.3 平行线的性质(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 15:01:59 | ||
图片预览




文档简介
(共30张PPT)
10.3 平行线的性质
学习目标及重难点
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;(重点)
2.能够根据平行线的性质进行简单的推理.
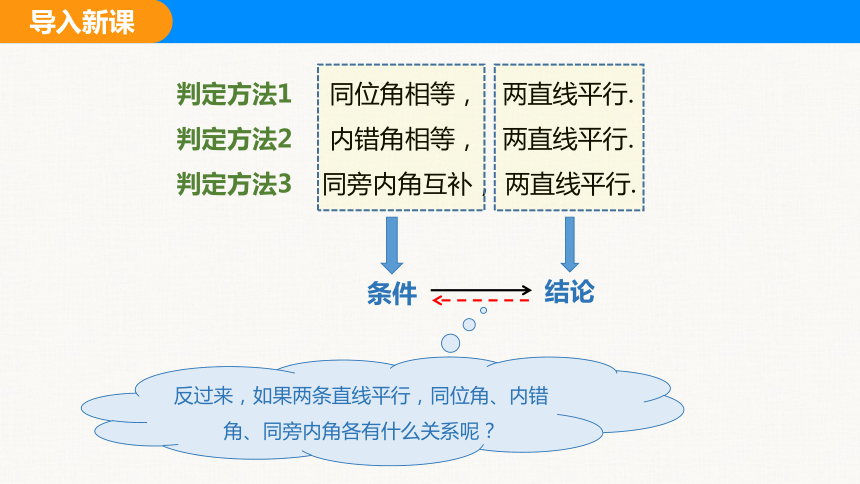
判定方法1 同位角相等, 两直线平行.
判定方法2 内错角相等, 两直线平行.
判定方法3 同旁内角互补, 两直线平行.
条件
结论
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
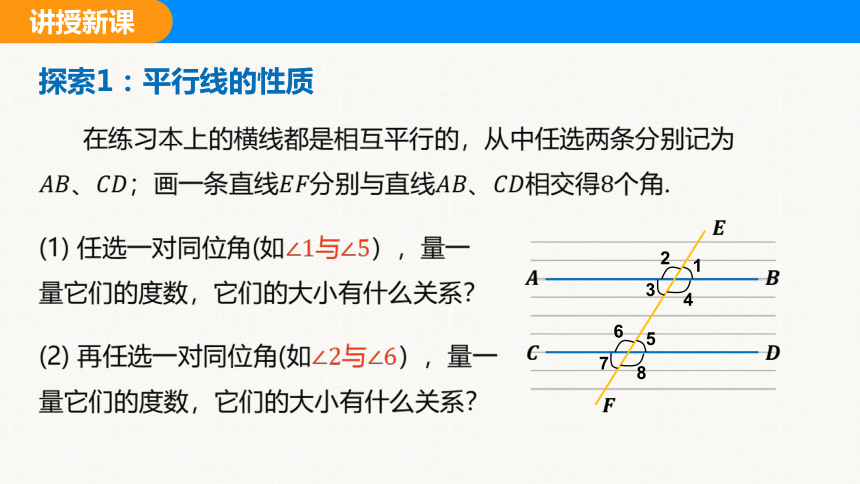
在练习本上的横线都是相互平行的,从中任选两条分别记为;画一条直线分别与直线相交得个角.
1
4
3
2
5
8
7
6
探索1:平行线的性质
(1) 任选一对同位角(如与),量一量它们的度数,它们的大小有什么关系?
(2) 再任选一对同位角(如与),量一量它们的度数,它们的大小有什么关系?
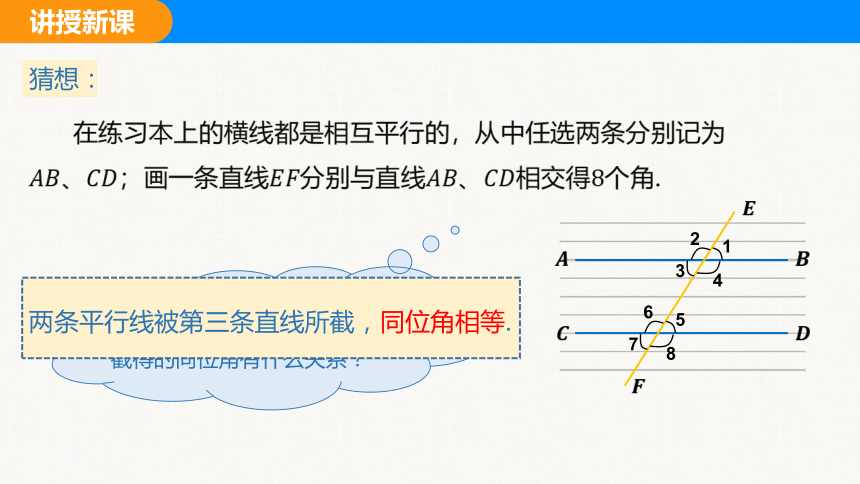
在练习本上的横线都是相互平行的,从中任选两条分别记为;画一条直线分别与直线相交得个角.
1
4
3
2
5
8
7
6
猜想两条平行线被第三条直线截得的同位角有什么关系?
两条平行线被第三条直线所截,同位角相等.
猜想:
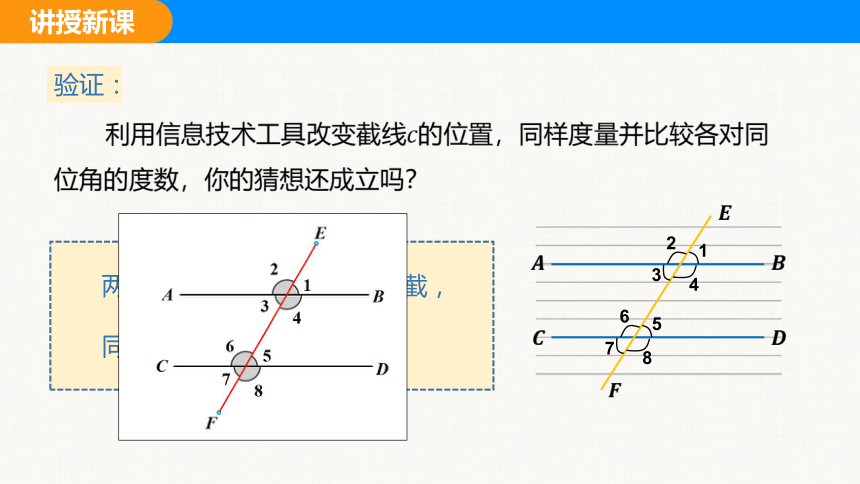
利用信息技术工具改变截线的位置,同样度量并比较各对同位角的度数,你的猜想还成立吗?
1
4
3
2
5
8
7
6
验证:
两条平行线被第三条直线所截,
同位角相等.
两条平行直线被第三条直线所截,同位角相等.
简单地说:两直线平行,同位角相等.
符号语言:
因为(已知),
所以(两直线平行,同位角相等).
平行线的性质1
a
b
c
1
2
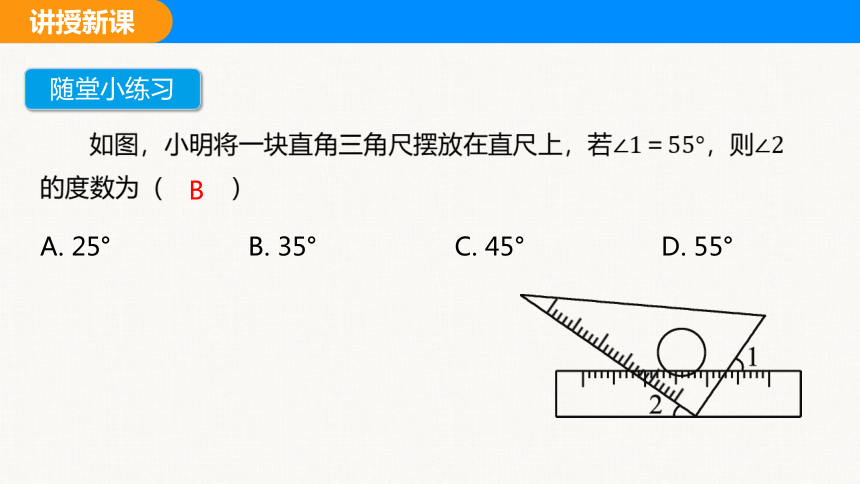
的度数为( B )
A. 25° B. 35° C. 45° D. 55°
B
随堂小练习
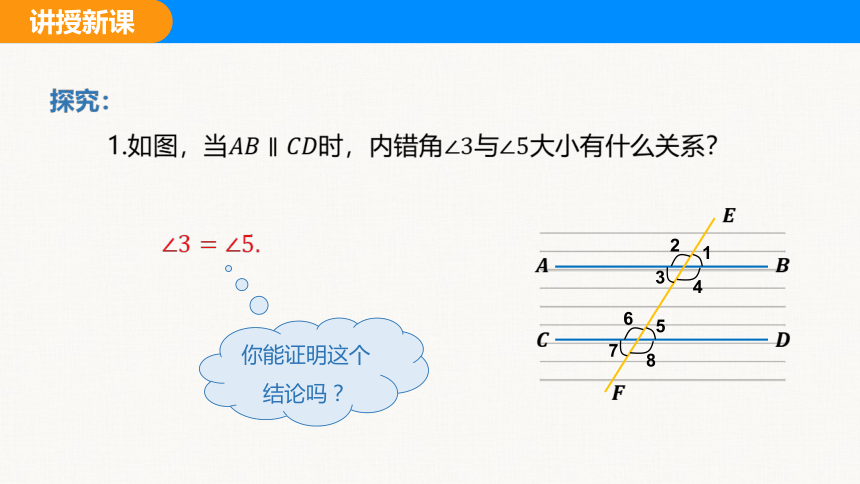
探究:
1.如图,当时,内错角与大小有什么关系?
1
4
3
2
5
8
7
6
你能证明这个结论吗?
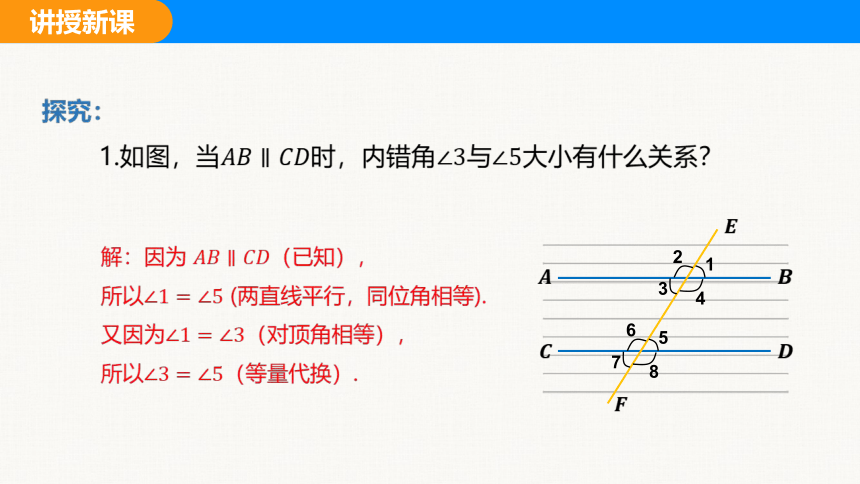
解:因为 (已知),
所以 (两直线平行,同位角相等).
又因为(对顶角相等),
所以(等量代换).
探究:
1.如图,当时,内错角与大小有什么关系?
1
4
3
2
5
8
7
6
两条平行直线被第三条直线所截,内错角相等.
简单地说:两直线平行,内错角相等.
符号语言:
因为(已知),
所以(两直线平行,内错角相等).
平行线的性质2
a
b
c
1
2
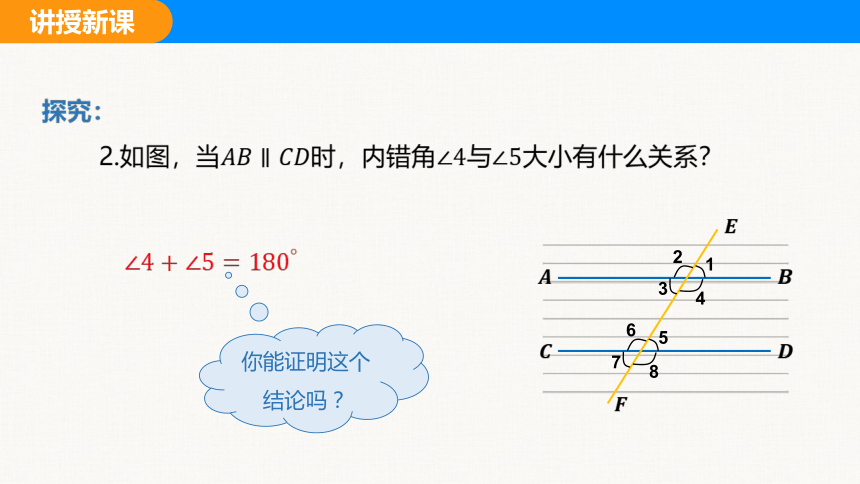
探究:
2.如图,当时,内错角与大小有什么关系?
1
4
3
2
5
8
7
6
你能证明这个结论吗?
解:因为 (已知),
所以 (两直线平行,同位角相等).
又因为(平角的定义),
所以(等量代换).
探究:
2.如图,当时,内错角与大小有什么关系?
1
4
3
2
5
8
7
6
两条平行直线被第三条直线所截,同旁内角互补.
简单地说:两直线平行,同旁内角互补.
符号语言:
因为(已知),
所以(两直线平行,同旁内角互补)
平行线的性质3
a
b
c
1
2
文字简述 符号语言 图示
两直线平行,同位角相等 因为(已知),所以________
两直线平行,内错角相等 因为已知),所以________ 两直线平行,同旁内角互补 因为(已知),所以______________
归纳总结
∠1=∠2
∠1=∠3
∠1+∠4=180°
b
a
c
3
2
1
4
看图填空:
(1)由,可以得到=_______,
依据是_________________________________;
(2)由,可以得到=_______,
依据是_________________________________;
(3)由,可以得到+_______=180°,
依据是_________________________________;
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
随堂小练习
看图填空:
(4)由,可以得到=_______,
依据是_________________________________;
(5)由,可以得到=_______,
依据是_________________________________.
两直线平行,内错角相等
两直线平行,同位角相等
随堂小练习
例1:如图,已知平分.若,则的度数是( )
A.40°
B.36°
C.35°
D.30°
C
例2:如图是一块梯形铁片的残余部分,量得,
梯形的另外两个角分别是多少度?
解:因为梯形上、下两底与互相平行,
根据“两直线平行,同旁内角互补”,可得
与互补,与互补,于是
所以梯形的另外两个角分别是
A
B
C
D
线的位置关系
角的数量关系
性质
判定
两直线平行
同位角相等
内错角相等
同旁内角互补
条件
结论
结论
条件
性质
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?
探索2:平行线的判定与性质
例3:如图,已知点分别在三角形的边上,且.
(1)求的度数;
(2)若是的平分线,且求的度数.
解:(1)因为 ,
所以°.
解:(2)因为平分,
所以
由,
得
且,
即
例3:如图,已知点分别在三角形的边上,且.
(2)若是的平分线,且求的度数.
因为,
所以
因为,
所以
已知:如图,试说明:
解:因为(已知),
所以 (同位角相等,两直线平行).
所以 (两直线平行,内错角相等).
因为(已知),
所以(垂直的定义).
所以 (同位角相等,两直线平行).
所以 (两直线平行,同位角相等).
所以 (等量代换).
随堂小练习
1.如图,则的度数是( )
A.105°
B.115°
C.125°
D.135°
B
习题1
2.已知,直线,把一块含有角的直角三角板如图放置,,三角板的斜边所在直线交于点,则=( )
A.50°
B.60°
C.70°
D.80°
B
习题2
3.将一个直角三角尺与两边平行的纸条如图放置,则下列结论正确的是 (填序号).
①∠1=∠2;
②∠4+∠5=180°;
③∠1+∠4=90°;
④∠4+90°=∠3.
①②③④
习题3
4.如图,一条水渠两次转弯后,和原来的方向相同.如果第一次的拐角是第二次的拐角是多少度?为什么?
解:是135°,理由如下:
∵水渠两次转弯后,和原来的方向相同,
∴,
∴
(两直线平行,内错角相等).
A
B
C
D
习题4
5.如图,直线分别与直线交于点平分平分,且. 试说明.
解:因为,
所以.
又因为平分平分,
所以
所以,
所以.
习题5
6.如图,,求的度数.
解:因为(已知),
(平角的定义),
所以(同角的补角相等).
所以 (内错角相等,两直线平行).
所以 (两直线平行,内错角相等).
又因为 (已知),
所以 (等量代换).
所以 (同位角相等,两直线平行).
所以(两直线平行,同位角相等).
习题6
性质 文字语言 符号语言 图示
性质1 两直线平行, 同位角相等 如果 , 那么
性质2 两直线平行, 内错角相等 如果 , 那么 性质3 两直线平行, 同旁内角互补 如果 那 么
10.3 平行线的性质
学习目标及重难点
1.掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;(重点)
2.能够根据平行线的性质进行简单的推理.
判定方法1 同位角相等, 两直线平行.
判定方法2 内错角相等, 两直线平行.
判定方法3 同旁内角互补, 两直线平行.
条件
结论
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
在练习本上的横线都是相互平行的,从中任选两条分别记为;画一条直线分别与直线相交得个角.
1
4
3
2
5
8
7
6
探索1:平行线的性质
(1) 任选一对同位角(如与),量一量它们的度数,它们的大小有什么关系?
(2) 再任选一对同位角(如与),量一量它们的度数,它们的大小有什么关系?
在练习本上的横线都是相互平行的,从中任选两条分别记为;画一条直线分别与直线相交得个角.
1
4
3
2
5
8
7
6
猜想两条平行线被第三条直线截得的同位角有什么关系?
两条平行线被第三条直线所截,同位角相等.
猜想:
利用信息技术工具改变截线的位置,同样度量并比较各对同位角的度数,你的猜想还成立吗?
1
4
3
2
5
8
7
6
验证:
两条平行线被第三条直线所截,
同位角相等.
两条平行直线被第三条直线所截,同位角相等.
简单地说:两直线平行,同位角相等.
符号语言:
因为(已知),
所以(两直线平行,同位角相等).
平行线的性质1
a
b
c
1
2
的度数为( B )
A. 25° B. 35° C. 45° D. 55°
B
随堂小练习
探究:
1.如图,当时,内错角与大小有什么关系?
1
4
3
2
5
8
7
6
你能证明这个结论吗?
解:因为 (已知),
所以 (两直线平行,同位角相等).
又因为(对顶角相等),
所以(等量代换).
探究:
1.如图,当时,内错角与大小有什么关系?
1
4
3
2
5
8
7
6
两条平行直线被第三条直线所截,内错角相等.
简单地说:两直线平行,内错角相等.
符号语言:
因为(已知),
所以(两直线平行,内错角相等).
平行线的性质2
a
b
c
1
2
探究:
2.如图,当时,内错角与大小有什么关系?
1
4
3
2
5
8
7
6
你能证明这个结论吗?
解:因为 (已知),
所以 (两直线平行,同位角相等).
又因为(平角的定义),
所以(等量代换).
探究:
2.如图,当时,内错角与大小有什么关系?
1
4
3
2
5
8
7
6
两条平行直线被第三条直线所截,同旁内角互补.
简单地说:两直线平行,同旁内角互补.
符号语言:
因为(已知),
所以(两直线平行,同旁内角互补)
平行线的性质3
a
b
c
1
2
文字简述 符号语言 图示
两直线平行,同位角相等 因为(已知),所以________
两直线平行,内错角相等 因为已知),所以________ 两直线平行,同旁内角互补 因为(已知),所以______________
归纳总结
∠1=∠2
∠1=∠3
∠1+∠4=180°
b
a
c
3
2
1
4
看图填空:
(1)由,可以得到=_______,
依据是_________________________________;
(2)由,可以得到=_______,
依据是_________________________________;
(3)由,可以得到+_______=180°,
依据是_________________________________;
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
随堂小练习
看图填空:
(4)由,可以得到=_______,
依据是_________________________________;
(5)由,可以得到=_______,
依据是_________________________________.
两直线平行,内错角相等
两直线平行,同位角相等
随堂小练习
例1:如图,已知平分.若,则的度数是( )
A.40°
B.36°
C.35°
D.30°
C
例2:如图是一块梯形铁片的残余部分,量得,
梯形的另外两个角分别是多少度?
解:因为梯形上、下两底与互相平行,
根据“两直线平行,同旁内角互补”,可得
与互补,与互补,于是
所以梯形的另外两个角分别是
A
B
C
D
线的位置关系
角的数量关系
性质
判定
两直线平行
同位角相等
内错角相等
同旁内角互补
条件
结论
结论
条件
性质
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?
探索2:平行线的判定与性质
例3:如图,已知点分别在三角形的边上,且.
(1)求的度数;
(2)若是的平分线,且求的度数.
解:(1)因为 ,
所以°.
解:(2)因为平分,
所以
由,
得
且,
即
例3:如图,已知点分别在三角形的边上,且.
(2)若是的平分线,且求的度数.
因为,
所以
因为,
所以
已知:如图,试说明:
解:因为(已知),
所以 (同位角相等,两直线平行).
所以 (两直线平行,内错角相等).
因为(已知),
所以(垂直的定义).
所以 (同位角相等,两直线平行).
所以 (两直线平行,同位角相等).
所以 (等量代换).
随堂小练习
1.如图,则的度数是( )
A.105°
B.115°
C.125°
D.135°
B
习题1
2.已知,直线,把一块含有角的直角三角板如图放置,,三角板的斜边所在直线交于点,则=( )
A.50°
B.60°
C.70°
D.80°
B
习题2
3.将一个直角三角尺与两边平行的纸条如图放置,则下列结论正确的是 (填序号).
①∠1=∠2;
②∠4+∠5=180°;
③∠1+∠4=90°;
④∠4+90°=∠3.
①②③④
习题3
4.如图,一条水渠两次转弯后,和原来的方向相同.如果第一次的拐角是第二次的拐角是多少度?为什么?
解:是135°,理由如下:
∵水渠两次转弯后,和原来的方向相同,
∴,
∴
(两直线平行,内错角相等).
A
B
C
D
习题4
5.如图,直线分别与直线交于点平分平分,且. 试说明.
解:因为,
所以.
又因为平分平分,
所以
所以,
所以.
习题5
6.如图,,求的度数.
解:因为(已知),
(平角的定义),
所以(同角的补角相等).
所以 (内错角相等,两直线平行).
所以 (两直线平行,内错角相等).
又因为 (已知),
所以 (等量代换).
所以 (同位角相等,两直线平行).
所以(两直线平行,同位角相等).
习题6
性质 文字语言 符号语言 图示
性质1 两直线平行, 同位角相等 如果 , 那么
性质2 两直线平行, 内错角相等 如果 , 那么 性质3 两直线平行, 同旁内角互补 如果 那 么
