【2025春新教材】人教版七年级下册数学10.3 实际问题与二元一次方程组(第2课时)(教学设计)
文档属性
| 名称 | 【2025春新教材】人教版七年级下册数学10.3 实际问题与二元一次方程组(第2课时)(教学设计) |

|
|
| 格式 | zip | ||
| 文件大小 | 900.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 00:00:00 | ||
图片预览



文档简介
/ 让教学更有效 高效备课 | 数学学科
10.3 实际问题与二元一次方程组(第2课时)教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第十章“二元一次方程组”10.3.2 实际问题与二元一次方程组(2),内容包括:能够根据具体的数量关系或图表信息,列出二元一次方程组解决较复杂的实际问题;掌握构建二元一次方程组解决较复杂的实际问题的基本步骤.
2.内容解析
本节课设置了较复杂的实际探究问题,让学生在探究如何利用二元一次方程组解决实际问题的过程中,分析问题中的各种数量关系,找出其中的相等关系,引进适当的未知数,列出相应的方程组,检验方程组的解是否符合实际意义等,从而进一步提高分析问题和解决问题的能力. 本节课的探究二,是一个开放性的问题,存在多种解决方法.通过解答这个问题,学生可以体验到同一个题目有多个解的情况,学会从不同的角度思考问题.
基于以上分析,确定本节课的教学重点为:能够根据具体的数量关系或图表信息,列出二元一次方程组解决较复杂的实际问题.
二、目标和目标解析
1.目标
(1)能够根据具体的数量关系或图表信息,列出二元一次方程组解决较复杂的实际问题.
(2)掌握构建二元一次方程组解决较复杂的实际问题的基本步骤.
(3)通过探究实际问题,进一步体会方程组是刻画现实世界数量关系的有效模型、发展模型观念.
2.目标解析
(1)面对较复杂的实际问题,如划分面积问题中,学生需要分析不同划分方式下各部分面积与总面积的关系. 这要求学生能从复杂情境中梳理出多个数量间的关系,准确设未知数并列出方程组. 当题目以图表形式呈现时,学生要能从图表中读取关键数据,通过对图表信息的提取和分析,转化为二元一次方程组,解决实际问题.
(2)在划分面积问题中,学生要将实际的场地划分简化为数学模型,忽略场地的地理位置、周边环境等无关因素,只关注形状、面积等数学要素,体现数学模型对现实复杂问题的近似刻画. 在较复杂的问题中,学生要深入挖掘潜在的等量关系,将这些等量关系转化为方程,运用方程思想解决问题.
(3)在划分面积问题中,学生要从实际的场地划分场景中,抽象出形状、面积等数学概念,用数学符号表示各区域的边长、面积等,培养学生从实际情境中提炼数学问题的能力. 面对复杂问题中的多种信息,学生要能整合这些信息,将其抽象为数学模型中的各个要素,提升信息整合和抽象概括能力. 在划分面积的开放性问题中,鼓励学生从不同角度思考划分方式,探索多种解决问题的方法. 如尝试不同的形状划分、不同的边长比例设置等,培养学生的创新思维,打破思维定式.
三、教学问题诊断分析
1.复杂数量关系梳理困难:在划分面积问题中,由于学生缺乏对复杂情境下数量关系的分析经验,导致它们面对多种划分方式时,难以梳理清楚各部分面积间复杂的几何关系.
2.图表信息提取偏差:当从图表中提取信息列方程时,部分学生不能准确解读图表数据,或者无法从图表中看出隐藏的信息,反映出学生对图表信息的理解和转化能力不足.
3.方程求解及应用错误:即便成功列出方程,在求解复杂方程组时,学生容易出现运算错误,特别是当方程中系数复杂或涉及分数、小数运算时. 这说明学生对计算的准确性和结果的合理性缺乏足够重视和检验能力.
基于以上分析,确定本节课的教学难点为:从实际情境中抽象出数学模型、准确找到等量关系列出二元一次方程组.
四、教学过程设计
(一)复习引入
问题 说一说用二元一次方程组解决简单实际问题的步骤.
(二)合作探究
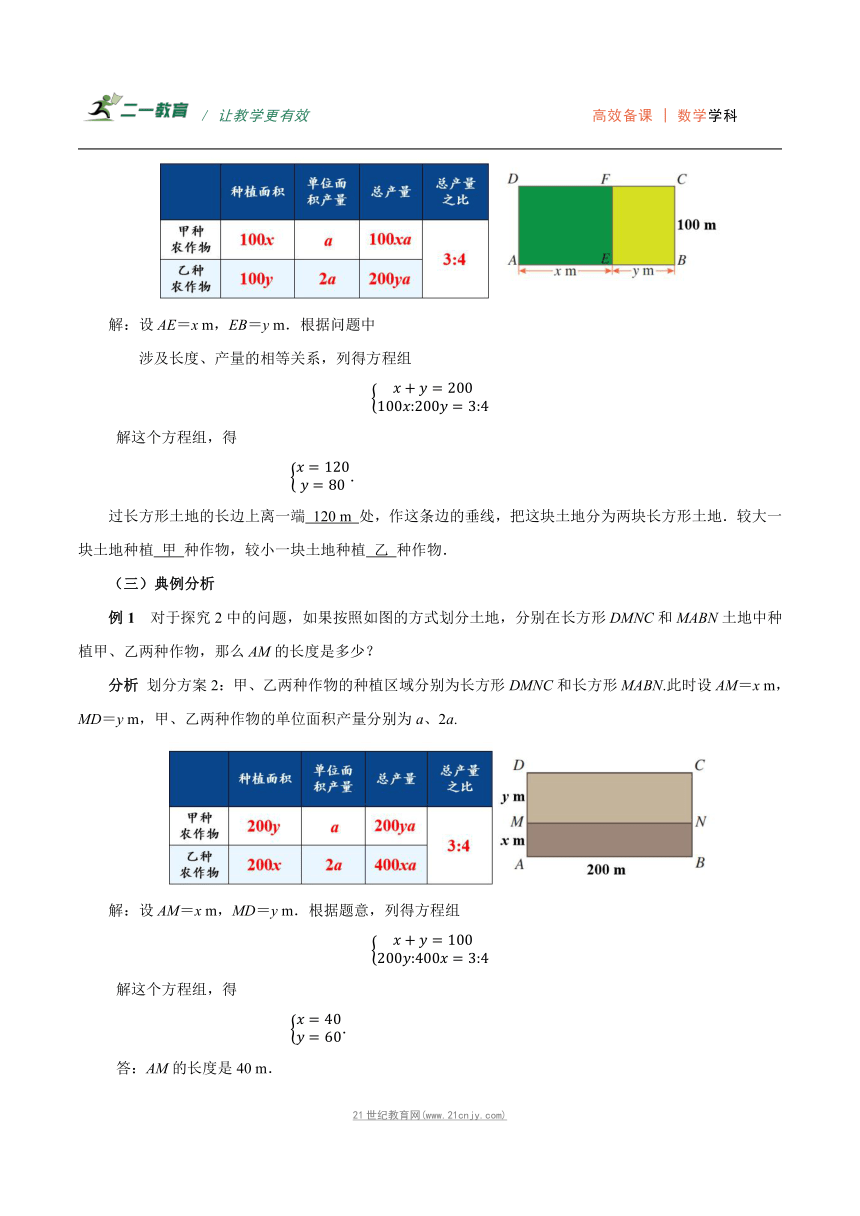
探究2 据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地划分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,才能使甲、乙两种作物的总产量的比是3:4
分析 划分方案1:甲、乙两种作物的种植区域分别为长方形AEFD和长方形EBCF.此时设AE=x m,EB=y m,甲、乙两种作物的单位面积产量分别为a、2a.
解:设AE=x m,EB=y m.根据问题中
涉及长度、产量的相等关系,列得方程组
解这个方程组,得
.
过长方形土地的长边上离一端 120 m 处,作这条边的垂线,把这块土地分为两块长方形土地.较大一块土地种植 甲 种作物,较小一块土地种植 乙 种作物.
(三)典例分析
例1 对于探究2中的问题,如果按照如图的方式划分土地,分别在长方形DMNC和MABN土地中种植甲、乙两种作物,那么AM的长度是多少?
分析 划分方案2:甲、乙两种作物的种植区域分别为长方形DMNC和长方形MABN.此时设AM=x m,MD=y m,甲、乙两种作物的单位面积产量分别为a、2a.
解:设AM=x m,MD=y m.根据题意,列得方程组
解这个方程组,得
.
答:AM的长度是40 m.
例2 如图,3×3的格子内填写了一些数和代数式.为了使格子的各行、各列及对角线上的三个数之和均相等,x,y各应取什么值?
解:根据题意,列得方程组
解得
答:x的值为-1,y的值为1.
例3 某地为打造运河风光带,雇用A,B两个工程队共同完成一段长为180 m的河道的清理任务.已知A工程队每天清理12 m,B工程队每天清理8 m,两个工程队工作天数之和为20天,A,B工程队分别清理了多长的河道?
解:设A工程队清理x m河道,B工程队清理y m河道.根据题意,列得方程组
解得
答:A工程队清理60 m河道,B工程队清理120 m河道.
设计意图:设置开放性的问题,能极大地激发学生的思维活力.从知识掌握角度,学生能通过不同划分方式,深化对数量关系的理解,将抽象知识具象化.在思维拓展上,能促使学生突破常规,学会从多元视角分析,培养创新思维.同时,在探讨多种解法时,还能提升学生的合作交流能力,使其在交流碰撞中完善思路,对知识的理解与运用达到新高度.
(四)巩固练习
1. 如图,8块相同的小长方形地砖拼成一个大长方形,大长方形的宽为60cm,每块小长方形地砖的长和宽分别是多少?如果设每块小长方形地砖的长和宽分别是x cm和y cm,则下列哪个方程组是错误的?(D)
A. B.
C. D.
2. 如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A,D两点分别与A′,D′对应,若,设∠CFD′=x°,∠CFE=y°,根据题意可得(D)
A. B.
C. D.
3.为打造集休闲娱乐、健身运动、观光旅游、体验自然等于一体的多功能活动区域.深圳湾公园海滨步道现有一段长350米的河边道路需整治,任务由A,B两个工程队先后接力完成,A工程队每天整治15米,B工程队每天整治10米,共用时30天.
根据题意,甲、乙两位同学分别列出了如下不完整的方程组:
甲: 乙:
从甲、乙两位同学所列方程组中任选一组,补全以下解题过程,并利用此方程组求出A,B两个工程队分别整治河边道路多少米.
解:选择的方程组为 .(填“甲”或“乙”)
设x为 .y为 .
解:若选择的方程组为甲,
则x为A工程队工作的天数,y为B工程队工作的天数;
若选择的方程组为乙,
则x为A工程队整治的河道长度,y为B工程队整治的河道长度.
故答案为:甲,A工程队工作的天数,B工程队工作的天数;(或乙,A工程队整治的河道长度,B工程队整治的河道长度).
若补全甲的方程组:,
解此方程组得,
∴15x=150,10y=200,
答:A,B两个工程队分别整治河边道路150米和200米.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
归纳总结
感受中考
1.(2023 西藏)列方程(组)解应用题
如图,巴桑家客厅的电视背景墙是由10块形状大小相同的长方形墙砖砌成.
(1)求一块长方形墙砖的长和宽;
(2)求电视背景墙的面积.
解:(1)设一块长方形墙砖的长为x m,宽为y m.
依题意得:,解得:,
答:一块长方形墙砖的长为1.2 m,宽为0.3 m.
(2)求电视背景墙的面积为:2×1.2×1.5=3.6(m2).
答:电视背景墙的面积为3.6m2.
2.(2024 河南)为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分表如下.
若要从这两种食品中摄入4600kJ热量和70g蛋白质,应选用A,B两种食品各多少包?
解:设选用A种食品x包,B种食品y包,
根据题意得:,
解得:.
答:应选用A种食品4包,B种食品2包.
3.(2023 宁波)茶叶作为浙江省农业十大主导产业之一,是助力乡村振兴的民生产业.某村有土地60公顷,计划将其中10%的土地种植蔬菜,其余的土地开辟为茶园和种植粮食,已知茶园的面积比种粮食面积的2倍少3公顷,问茶园和种粮食的面积各多少公顷?设茶园的面积为x公顷,种粮食的面积为y公顷,可列方程组为(B)
A. B.
C. D.
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(七)小结梳理
(八)布置作业
1.必做题:习题10.3 第5、6题.
2.探究性作业:习题10.3 第9题.
21世纪教育网(www.21cnjy.com)
10.3 实际问题与二元一次方程组(第2课时)教学设计
一、内容和内容解析
1.内容
本节课是人教版《义务教育教科书 数学》七年级下册(以下统称“教材”)第十章“二元一次方程组”10.3.2 实际问题与二元一次方程组(2),内容包括:能够根据具体的数量关系或图表信息,列出二元一次方程组解决较复杂的实际问题;掌握构建二元一次方程组解决较复杂的实际问题的基本步骤.
2.内容解析
本节课设置了较复杂的实际探究问题,让学生在探究如何利用二元一次方程组解决实际问题的过程中,分析问题中的各种数量关系,找出其中的相等关系,引进适当的未知数,列出相应的方程组,检验方程组的解是否符合实际意义等,从而进一步提高分析问题和解决问题的能力. 本节课的探究二,是一个开放性的问题,存在多种解决方法.通过解答这个问题,学生可以体验到同一个题目有多个解的情况,学会从不同的角度思考问题.
基于以上分析,确定本节课的教学重点为:能够根据具体的数量关系或图表信息,列出二元一次方程组解决较复杂的实际问题.
二、目标和目标解析
1.目标
(1)能够根据具体的数量关系或图表信息,列出二元一次方程组解决较复杂的实际问题.
(2)掌握构建二元一次方程组解决较复杂的实际问题的基本步骤.
(3)通过探究实际问题,进一步体会方程组是刻画现实世界数量关系的有效模型、发展模型观念.
2.目标解析
(1)面对较复杂的实际问题,如划分面积问题中,学生需要分析不同划分方式下各部分面积与总面积的关系. 这要求学生能从复杂情境中梳理出多个数量间的关系,准确设未知数并列出方程组. 当题目以图表形式呈现时,学生要能从图表中读取关键数据,通过对图表信息的提取和分析,转化为二元一次方程组,解决实际问题.
(2)在划分面积问题中,学生要将实际的场地划分简化为数学模型,忽略场地的地理位置、周边环境等无关因素,只关注形状、面积等数学要素,体现数学模型对现实复杂问题的近似刻画. 在较复杂的问题中,学生要深入挖掘潜在的等量关系,将这些等量关系转化为方程,运用方程思想解决问题.
(3)在划分面积问题中,学生要从实际的场地划分场景中,抽象出形状、面积等数学概念,用数学符号表示各区域的边长、面积等,培养学生从实际情境中提炼数学问题的能力. 面对复杂问题中的多种信息,学生要能整合这些信息,将其抽象为数学模型中的各个要素,提升信息整合和抽象概括能力. 在划分面积的开放性问题中,鼓励学生从不同角度思考划分方式,探索多种解决问题的方法. 如尝试不同的形状划分、不同的边长比例设置等,培养学生的创新思维,打破思维定式.
三、教学问题诊断分析
1.复杂数量关系梳理困难:在划分面积问题中,由于学生缺乏对复杂情境下数量关系的分析经验,导致它们面对多种划分方式时,难以梳理清楚各部分面积间复杂的几何关系.
2.图表信息提取偏差:当从图表中提取信息列方程时,部分学生不能准确解读图表数据,或者无法从图表中看出隐藏的信息,反映出学生对图表信息的理解和转化能力不足.
3.方程求解及应用错误:即便成功列出方程,在求解复杂方程组时,学生容易出现运算错误,特别是当方程中系数复杂或涉及分数、小数运算时. 这说明学生对计算的准确性和结果的合理性缺乏足够重视和检验能力.
基于以上分析,确定本节课的教学难点为:从实际情境中抽象出数学模型、准确找到等量关系列出二元一次方程组.
四、教学过程设计
(一)复习引入
问题 说一说用二元一次方程组解决简单实际问题的步骤.
(二)合作探究
探究2 据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200 m、宽100 m的长方形土地划分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,才能使甲、乙两种作物的总产量的比是3:4
分析 划分方案1:甲、乙两种作物的种植区域分别为长方形AEFD和长方形EBCF.此时设AE=x m,EB=y m,甲、乙两种作物的单位面积产量分别为a、2a.
解:设AE=x m,EB=y m.根据问题中
涉及长度、产量的相等关系,列得方程组
解这个方程组,得
.
过长方形土地的长边上离一端 120 m 处,作这条边的垂线,把这块土地分为两块长方形土地.较大一块土地种植 甲 种作物,较小一块土地种植 乙 种作物.
(三)典例分析
例1 对于探究2中的问题,如果按照如图的方式划分土地,分别在长方形DMNC和MABN土地中种植甲、乙两种作物,那么AM的长度是多少?
分析 划分方案2:甲、乙两种作物的种植区域分别为长方形DMNC和长方形MABN.此时设AM=x m,MD=y m,甲、乙两种作物的单位面积产量分别为a、2a.
解:设AM=x m,MD=y m.根据题意,列得方程组
解这个方程组,得
.
答:AM的长度是40 m.
例2 如图,3×3的格子内填写了一些数和代数式.为了使格子的各行、各列及对角线上的三个数之和均相等,x,y各应取什么值?
解:根据题意,列得方程组
解得
答:x的值为-1,y的值为1.
例3 某地为打造运河风光带,雇用A,B两个工程队共同完成一段长为180 m的河道的清理任务.已知A工程队每天清理12 m,B工程队每天清理8 m,两个工程队工作天数之和为20天,A,B工程队分别清理了多长的河道?
解:设A工程队清理x m河道,B工程队清理y m河道.根据题意,列得方程组
解得
答:A工程队清理60 m河道,B工程队清理120 m河道.
设计意图:设置开放性的问题,能极大地激发学生的思维活力.从知识掌握角度,学生能通过不同划分方式,深化对数量关系的理解,将抽象知识具象化.在思维拓展上,能促使学生突破常规,学会从多元视角分析,培养创新思维.同时,在探讨多种解法时,还能提升学生的合作交流能力,使其在交流碰撞中完善思路,对知识的理解与运用达到新高度.
(四)巩固练习
1. 如图,8块相同的小长方形地砖拼成一个大长方形,大长方形的宽为60cm,每块小长方形地砖的长和宽分别是多少?如果设每块小长方形地砖的长和宽分别是x cm和y cm,则下列哪个方程组是错误的?(D)
A. B.
C. D.
2. 如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A,D两点分别与A′,D′对应,若,设∠CFD′=x°,∠CFE=y°,根据题意可得(D)
A. B.
C. D.
3.为打造集休闲娱乐、健身运动、观光旅游、体验自然等于一体的多功能活动区域.深圳湾公园海滨步道现有一段长350米的河边道路需整治,任务由A,B两个工程队先后接力完成,A工程队每天整治15米,B工程队每天整治10米,共用时30天.
根据题意,甲、乙两位同学分别列出了如下不完整的方程组:
甲: 乙:
从甲、乙两位同学所列方程组中任选一组,补全以下解题过程,并利用此方程组求出A,B两个工程队分别整治河边道路多少米.
解:选择的方程组为 .(填“甲”或“乙”)
设x为 .y为 .
解:若选择的方程组为甲,
则x为A工程队工作的天数,y为B工程队工作的天数;
若选择的方程组为乙,
则x为A工程队整治的河道长度,y为B工程队整治的河道长度.
故答案为:甲,A工程队工作的天数,B工程队工作的天数;(或乙,A工程队整治的河道长度,B工程队整治的河道长度).
若补全甲的方程组:,
解此方程组得,
∴15x=150,10y=200,
答:A,B两个工程队分别整治河边道路150米和200米.
设计意图:学完新知识后及时进行课堂巩固练习,不仅可以强化学生对新知的记忆,加深学生对新知的理解,还可以及时反馈学习情况,帮助学生查漏补缺,帮助教师及时调整教学策略.
归纳总结
感受中考
1.(2023 西藏)列方程(组)解应用题
如图,巴桑家客厅的电视背景墙是由10块形状大小相同的长方形墙砖砌成.
(1)求一块长方形墙砖的长和宽;
(2)求电视背景墙的面积.
解:(1)设一块长方形墙砖的长为x m,宽为y m.
依题意得:,解得:,
答:一块长方形墙砖的长为1.2 m,宽为0.3 m.
(2)求电视背景墙的面积为:2×1.2×1.5=3.6(m2).
答:电视背景墙的面积为3.6m2.
2.(2024 河南)为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分表如下.
若要从这两种食品中摄入4600kJ热量和70g蛋白质,应选用A,B两种食品各多少包?
解:设选用A种食品x包,B种食品y包,
根据题意得:,
解得:.
答:应选用A种食品4包,B种食品2包.
3.(2023 宁波)茶叶作为浙江省农业十大主导产业之一,是助力乡村振兴的民生产业.某村有土地60公顷,计划将其中10%的土地种植蔬菜,其余的土地开辟为茶园和种植粮食,已知茶园的面积比种粮食面积的2倍少3公顷,问茶园和种粮食的面积各多少公顷?设茶园的面积为x公顷,种粮食的面积为y公顷,可列方程组为(B)
A. B.
C. D.
设计意图:在学习完知识后加入中考真题练习,不仅可以帮助学生明确考试方向,熟悉考试题型,检验学习成果,提升应考能力,还可以提升学生的学习兴趣和动力.
(七)小结梳理
(八)布置作业
1.必做题:习题10.3 第5、6题.
2.探究性作业:习题10.3 第9题.
21世纪教育网(www.21cnjy.com)
同课章节目录
