07 数量关系(答案)—2025年小升初数学专项训练(人教版)
文档属性
| 名称 | 07 数量关系(答案)—2025年小升初数学专项训练(人教版) |  | |
| 格式 | docx | ||
| 文件大小 | 305.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 08:07:29 | ||
图片预览




文档简介
2025年小升初数学奥数专项训练(人教版)
07 数量关系
一、单选题
1.大毛骑车上学,去时每小时行18千米,回来时每小时行12千米,则大毛往返平均速度为( )千米/时.
A.108 B.14.4 C.15 D.16.2
2.“高原精灵”藏羚羊是国家一级保护动物,每年5月,藏羚羊开始一年一度的迁徙产仔之旅,它的速度达到1320米/分,藏羚羊每秒能行多少米?解决这个问题所用的数量关系是( )。
A.路程÷时间=速度 B.路程÷速度=时间 C.速度×时间=路程
3.在比例尺是1:500的图纸上,测得一块长方形的土地长5厘米,宽4厘米,这块土地的实际面积是( )平方米。
A.20 B.500 C.5000 D.50
4.某品牌免洗抑菌洗手液一瓶50元,买5瓶送1瓶,750元最多可以买( )瓶。
A.16 B.18 C.20
5.王阿姨目前使用的手机话费套餐如下:月基本话费是58元,这款套餐包含80分钟免费通话时间和20G基本流量,通话超出部分按每分钟0.19元计算,流量超出部分按10元/G计算。王阿姨12月份一共通话120分钟,使用流量18G,那么她这个月需要支付话费( )元。
A.7.6 B.65.6 C.73.2 D.80.8
6.下列运动中,奔跑速度最快的是( )。
A.狮子:6分钟8千米 B.兔子:5分钟4500米
C.斑马:1000米/分 D.马:60千米/时
7.停车场对小汽车的收费标准如下, 半小时即以内免费,半小时以上每过一小时收费八元, 不足一小时按一小时算。如果一辆汽车付停车费 24 元,那么它的停车时间段可能是( )
A.12:30~14:30 B.10:00~12:35
C.13:25~14:45 D.8:15-12:00
8.小小和妈妈沿着圆形花坛散步。小小走一圈用12分钟,妈妈走一圈用8分钟。如果两人同时同地出发,相背而行,走了16分钟后,两人的位置是下面的图( )。
A. B.
C. D.
9.甲、乙两辆垃圾清运车从垃圾处理站出发回收垃圾。两车背向而行,行驶了0.5h后,两车相距85km,甲、乙两车的速度比是8∶9,乙车比甲车每小时快( ) km。
A.15 B.12 C.10 D.20
10.小芳和小红同时从 A、B两城出发,相向而行,16小时后在途中相遇,已知小芳比小红速度快,那么小芳从A城到B城要用( )小时。
A.20 B.24 C.31 D.32
11.夜晚,奇奇和爸爸在路边散步,从第1个路灯到第19个路灯,共花了10分钟(相邻路灯间距离相等)。奇奇和爸爸的步行速度是1.2米/秒,相邻两个路灯之间的距离是( )米。
A.0.6 B.30 C.36 D.40
二、填空题
12.一辆汽车2小时行了125千米,这辆汽车所行驶路程和时间的比是 ,比值是 ,这个比值表示 。
13.张良沿一公路徒步,速度为每小时4.2千米。沿该路的公共汽车每36分钟就有一辆车从后面超过他。每12分钟就又遇到迎面开来的一辆车,如果公共汽车按相等的时间间隔,以同一速度前行,那么,公共汽车发出时间间隔是 ?
14.一辆汽车6时行驶了 540 km,路程与时间的比是 ,比值是 ,这个比值表示 。
15.在一幅比例尺为1:3000000的地图上,量得A、B两地相距12cm,则A、B两地实际相距 km。一辆货车从A地开往B地,每小时行驶80km,需要 小时才能到达。
16.为了丰富校园文体生活,提高 路程/m学生的身体素质,培养学生养成良好的锻炼习惯,让学生在体育锻炼中感受积极健康的生活,学校组织全校学生开展冬季晨跑活动。六年级学生每天晨跑的目标是600 m,上面是成成和嘟嘟跑步的路程与时间的关系图。
(1)成成跑完全程用时 分,当成成跑完全程后,嘟嘟又跑 分才跑完全程。
(2)成成跑步的路程与时间的比是 ,比值是 比值表示的是 。
17.元旦迎新会上,401 班要买40套演出服。商场正在“买4送1”活动。如果演出服120元/套,请问401班至少需要付 元。
18.商店购进一批每双6.50元的凉鞋,售价为7.40元,当卖到还到5双时,除去全部成本外还获利44元,那么这批凉鞋会共有 双。
19.家住西樵山下,年过六旬的吴大爷秋日步行锻炼,他从西樵山北门牌坊出发,每行5分钟就休息2分钟,匀速前进,步行50分钟到达终点翠岩牌坊。已知吴大爷最后一次休息时离翠岩牌坊还有70米。那么:吴大爷在途中休息用了 分钟;吴大爷步行的速度是每分钟 米。
20.一座大桥长2400米。一列火车通过大桥时每分钟行940米,从车头上桥到车尾离桥共需 3 分钟,这列火车长 米。
21.一辆汽车从甲地开往Z地,行前一半时间的速度和行后一半时间的速度之比是7:9 ,那么行前一半路程和行后一半路程的时间之比是 。
22.甲、乙两车从同一地点出发沿同一高速公路从A地到B地.甲车先出发2小时,乙车出发后经5小时与甲车同时到达B地,如果乙车时速增加8千米.那么,出发后4小时可追上甲车.A地与B地的距离是 千米。
三、解答题
23.奇奇和妙妙从圆形广场的同一地点背对背出发,5分钟后两个人相遇,妙妙步行的速度是65米/分,奇奇步行的速度是68米/分,这个圆形广场的半径约为多少米?(结果保留整数)
24.妈妈买回3千克大米和12千克大豆,共付了人民币67.5元,已知每千克大米6.5元,每千克大豆多少元?
25.已知A、B两地相距840米,甲、乙两人分别从A、B两地同时出发,相向而行,6分钟相遇,若同向而行,70分钟后甲可以追上乙,问甲从A地出发走到B地要用多少分钟?
26.某品牌大米原来的单价是每千克4.8元,活动促销价是每千克4.5元。奶奶用原价买60千克的钱,现在可以买多少千克大米?
27.在比例尺是1:400000的地图上量得甲、乙两地相距9cm,一列货车和一列客车分别从甲,乙两地同时开出,相向而行,2小时相遇,已知客车与货车的速度比是5:4,客车的速度是多少?
28.一辆客车和一辆货车同时分别从甲城、乙城相向开出,4小时后两车相遇,客车比货车多行50千米。已知货车速度是客车的速度的,求甲城和乙城相距多少千米。(用方程解答)
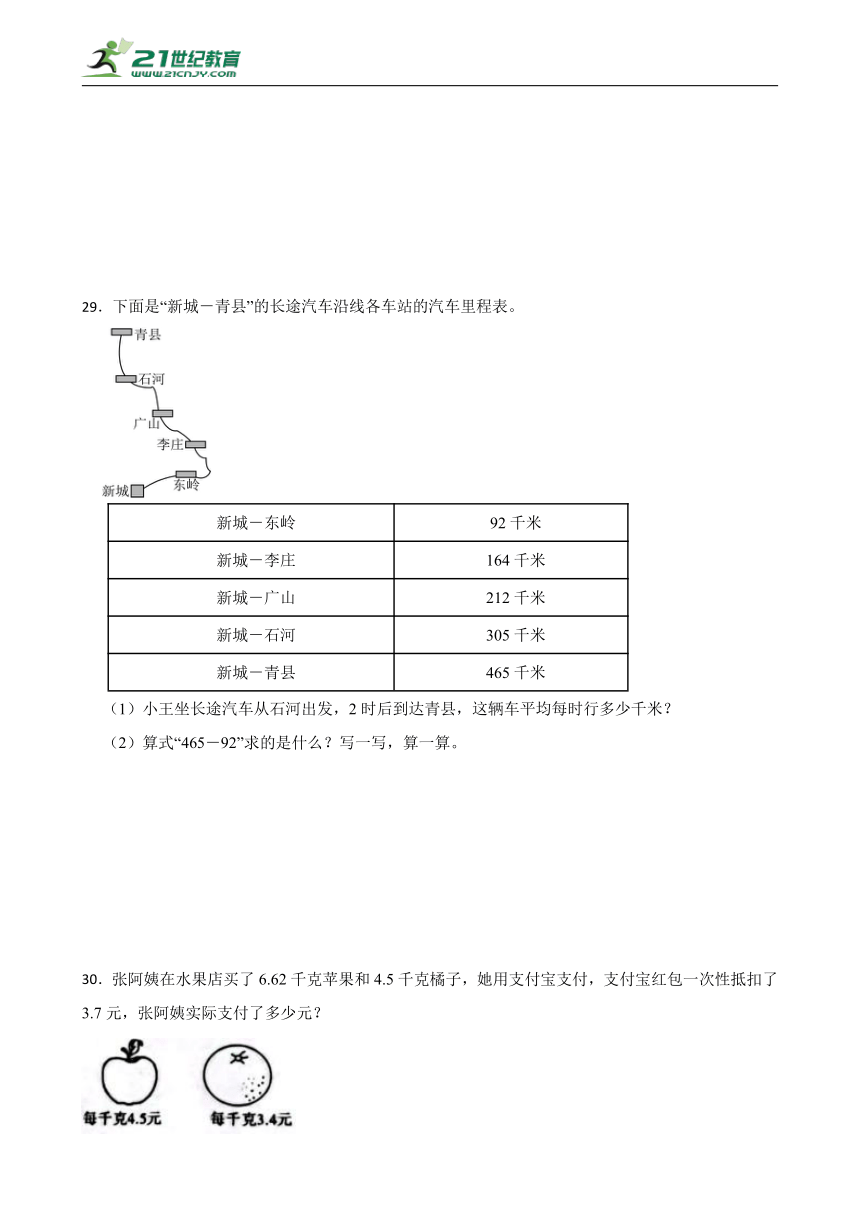
29.下面是“新城-青县”的长途汽车沿线各车站的汽车里程表。
新城-东岭 92千米
新城-李庄 164千米
新城-广山 212千米
新城-石河 305千米
新城-青县 465千米
(1)小王坐长途汽车从石河出发,2时后到达青县,这辆车平均每时行多少千米?
(2)算式“465-92”求的是什么?写一写,算一算。
30.张阿姨在水果店买了6.62千克苹果和4.5千克橘子,她用支付宝支付,支付宝红包一次性抵扣了3.7元,张阿姨实际支付了多少元?
31.A、B两地,甲乙两人骑自行车行驶全程所用的时间之比为4:5,如果甲乙两人分别同时从A、B两地相对行驶,40分钟后两人相遇,相遇后各自继续前行,那么乙到达A地比甲到达B地要晚多少分钟?
32. 前进小学要去秋游,有学生60人,老师为学生准备了午餐,有火腿肠、冰红茶和汉堡,每人一份。火腿肠每根3.5元,冰红茶每瓶2.58元,汉堡每个4.85元。后来老师发现商场正在搞促销,汉堡买四赠一,冰红茶买五赠一。老师用600元准备午餐够吗?
答案解析部分
1.B
解:假设家到学校的距离为1千米。
(1+1)÷(+)
=2÷
=14.4(千米/时);
故答案为:B。
假设家到学校的距离为1千米,则去时用了小时,回来用了小时,往返一共行了1+1=2(千米),用往返的总路程除以往返用的总时间即可求出往返的平均速度,据此解答。
2.A
解:用1320÷60来计算,用的数量关系是路程÷时间=速度。
故答案为:A。
速度×时假=路程,路程÷速度=时间,路程÷时间=速度,求每秒能行的长度就是求速度。
3.B
解:5÷÷100
=2500÷100
=25(米)
4÷÷100
=2000÷100
=20(米)
25×20=500(平方米)。
故答案为:B。
这块土地的实际面积=实际长×实际宽;其中,实际距离=图上距离÷比例尺,然后单位换算。
4.B
解:5+1=6(瓶)
50×5=250(元)
750÷250=3(组)
3×6=18(瓶)。
故答案为:B。
买5瓶送1瓶,因此可以把6瓶洗手液看作一组,一组的总价=单价×5瓶,组数=总价÷平均每组的钱数,最后再乘6即可。
5.B
解:(120-80)×0.19+58
=40×0.19+58
=7.6+58
=65.6(元)
故答案为:B。
通话时长超出80分钟,要加收费用。流量使用少于20G,不需要加收费用。用120减去80求出超出的时间,用超出的时间乘0.19求出超出80分钟的费用,再加上基本话费即可求出这个月需要支付的话费。
6.A
解:8000÷6=1333(米)……2(米)
4500÷5=900(米)
1时=60分钟
60000÷60=1000(米)
1333>1000>900
狮子的速度最快。
故答案为:A。
速度=路程÷时间,先单位换算,分别计算出平均每分钟跑的米数,然后再比较大小。
7.B
解:24÷8+0.5
=3+0.5
=3.5(小时)。
A项:14时30分-12时30分=2小时,不符合题意。
B项:12时35分-10时=2小时35分,不足一小时按一小时算,所以该停车时长为3小时,符合题意。
C项:14时45分-13时25分=1小时20分,不足一小时按一小时算,所以该停车时长为2小时,不符合题意。
D项:12时-8时15分=3小时45分,根据题目的要求,不足一小时按一小时算,所以该停车时长为4小时,不符合题意。
故答案为:B。
此题考查的是对时间段和收费标准的理解与应用。首先根据题目的要求,确定24元停车费对应的实际停车时长。然后,分别计算出四个选项的停车时长,注意将不足一小时的时间段按一小时计费。最后,比较四个选项的停车时长与实际时长,找出符合题意的选项。
8.C
解:16÷12=1(圈)······4(分钟)
16÷8=2(圈), 能表示两人的位置。
故答案为:C。
走了16分钟后,小小走了1圈加上一圈的处,妈妈刚好走2圈,据此选择。
9.C
甲车1小时行驶的路程:85×÷0.5=80(千米)
乙车1小时行驶的路程:85×÷0.5=90(千米)
90-80=10(千米)
故答案为:C
先分别用两车行驶的路程乘两车各自行驶路程占总路程的分率,求出甲、乙两车0.5小时各行驶的路程,再除以0.5求出每小时各行驶的路程,再相减即可。
10.C
设小红的速度为v,则小芳的速度为v+v= v ,两人的速度和是v+v=v,根据路程=速度和×相遇时间可知,A、B两城之间的距离为v×16,用两城之间的距离除以小芳的速度,即为小芳从A城到B城所需要的时间,列式计算为:v×16÷v=×15=31(小时)。
故答案为:C
解决此题的关键是根据小芳比小红速度快,用含有字母的式子表示出小红和小芳的速度,再根据相遇的时间用含有字母的式子表示出A、B两城之间的距离,最后用两城之间的距离除以小芳的速度,即可求出小芳从A城到B城要用的时间。
11.D
解:1.2×10×60=720(米),720÷(19-1)=40(米),
故答案为:D
本题属于两端都栽的植树问题,所以间隔数=棵数-1,根据路程=速度×时间计算出从第1个路灯到第19个路灯的总长度,用总长度÷间隔数即可知道相邻两个路灯之间的距离.
12.125:2;;汽车每小时行驶的速度
解:路程∶时间=125∶2;比值是125∶2=;这个比值表示:这辆汽车每小时行驶的路程。
故答案为:125∶2;;汽车每小时行驶的速度。
比是由一个前项和一个后项组成的除法算式,只不过把“÷”(除号)改成了":"(比号)而已,但除法算式表示的是一种运算,而比则表示两个数的关系。比值: 比的前项除以比的后项所得到的数。
13.18
解:设汽车速度为每小时x千米。
36分= 0.6小时12分=0.2小时
0.6(x - 4.2) = 0.2(x+4.2)
解得:x=8.4
汽车与张良的速度差为:8.4-4.2=4.2(千米/时)
发车间隔为:4.2 x0.6÷8.4= 2.52÷8.4=0.3(小时),0.3小时= 18分钟
故答案为:18。
根据题意,先求出汽车与张良的速度差和速度和,再根据和差公式求出汽车的速度,再根据追及问题求出追及路程,用追及路程除以汽车的速度,就是汽车发车的间隔时间。
14.90:1;90;这辆汽车的平均速度
解:汽车所行驶的路程和时间的比:540∶6=(540÷6)∶(6÷6)=90∶1
比值:90÷1=90
比值表示:汽车每小时行驶的路程,即速度。
故答案为:90:1;90;这辆汽车的平均速度
根据题意,求汽车行驶的路程和时间的比,也就是求540和6的比,然后根据比的性质进行化简;比的前项除以比的后项,求出的商就是比值,路程÷时间=速度,据此解答。
15.360;4.5
解:12÷÷100000
=36000000÷100000
=360(千米)
360÷80=4.5(小时)。
故答案为:360;4.5。
实际距离=图上距离÷比例尺;然后单位换算;到达需要的时间=路程÷速度。
16.(1)4;1
(2)150:1;150;速度
解:(1)根据题图,成成跑完全程用时4分;
5-4=1(分)
当成成跑完全程后,嘟嘟又跑1分才跑完全程。
(2)600:4=150:1=150
这个比值表示的是速度。
故答案为:4;1;150:1;150;速度。
(1)根据题图可以分别找到成成和嘟嘟跑步的时间。
(2)从图中可以找到成成跑步的路程和时间,两数相比并求值即可;速度=路程÷时间,比值表示的是时间。
17.3840元
解:40÷(4+1)
=40÷5
=8(组)
8×4×120=3840(元)
故答案为:3840。
“买4送1”表示花4套的价钱买5套,先求出40里面有几个5,那么需要付的钱数=几×4×一套演出服的价钱,据此代入数值作答即可。
18.90
解:设这批凉鞋共有x双。
7.40(x-5)- 6.50x = 44
7.4x-37-6.5x=44
0.9x=81
x=90
故答案为:90
设这批凉鞋共有x双,先计算购进凉鞋的总成本=单价×数量,即6.50x双;再计算售出凉鞋的总收入=单价×数量,即7.40(x-5)双;因售出凉鞋的总收入比购进凉鞋的总成本多44元,所以可以列出关于x的方程:7.40(x-5)- 6.50x = 44,解方程即可求出答案。
19.14;70
解:50÷(5+2)
=50÷7
=7(次)······1(分)
休息:7×2=14(分)
步行:50-14=36(分)
速度:70÷1=70(米/分)。
故答案为:14;70。
先用总时间÷每次周期的时间=周期数······余下的时间,则最后一分钟仍然在步行,所以步行时间是36分,休息时间是14分钟,最后一次休息时离翠岩牌坊还有70米,则这70米步行用了1分钟,所以速度是70米/分。
20.420
解:如图:
940×3-2400
=2820-2400
=420(米)
这列火车长420米
故答案为:420。
火车长+桥长=火车行驶的路程,据此推出:火车长=火车行驶的路程-桥长。
21.5:4
解:设一半时间为“1”,则总路程是:
1×7+1×9
=7+9
=16
前一半路程为:16÷2=8
用时为:(8-1×7)÷9+1
=1÷9+1
=
后一半路程用时为:16÷2÷9
=8÷9
=
时间比是为::=10:9=5:4。
故答案为:5:4。
“对半”行程问题,设一半时间为“1”,然后求出总路程,再将总路程平分,则一半路程为:16÷2=8,前一半时间所行路程为7,则前一半路程的时间为,进而求出后一半路程所用时间,写出比后,依据比的基本性质化简比。
22.560
解:甲与乙的速度比为5∶(2+5)=5∶7
故设甲的速度为5v千米/小时,乙的速度为7x千米/小时。
4×(7v+8)=(4+2)×5v
28v+32=30v
2v=32
v=16
5×16×7=560(千米)
故答案为:560。
根据“甲车先出发2小时,乙车出发后经5小时与甲车同时到达B地”可知甲乙两车走相同路程(AB两地的距离),用时为5+2=7、5小时,则他们的速度比为5:7,由此可设出甲的速度为5v千米/小时,乙的速度为7v千米/小时;之后根据“如果乙车时速增加8千米,那么,出发后4小时可追上甲车”便可列出一方程4×(7v+8)=(4+2)×5v,求得v的值,即可得到甲、乙的速度,之后就可据“速度×时间=距离”得出问题答案。
23.解:(65+68)×5
=133×5
=665(m)
665÷3.14÷2≈106(m)
答:这个圆形广场的半径约为 106 m。
“奇奇和妙妙从圆形广场的同一地点背对背出发,5分钟后两个人相遇 ”,即5分钟两人走的路程,就是圆形广场的周长。“ 妙妙步行的速度是65米/分,奇奇步行的速度是68米/分 ”,所以5分钟两人的路程合计为(65+68)×5=665(m),因此圆形广场的周长也是665m。根据公式“圆周长=2πr”,因此圆形广场的半径就是665÷3.14÷2≈106(m)。
24.解:(67.5-6.5×3)÷12
=(67.5-19.5)÷12
=48÷12
=4(元)
答:每千克大豆4元。
每千克大米的钱数×3=3千克大米的钱数,总钱数-3千克大米的钱数=买大豆花的钱数,买大豆花的钱数÷大豆买的质量=大豆的单价。
25.解:速度和:840÷6=140(米/分),
速度差:840÷70=12(米/分),
甲:(140+12)÷2=76(米/分)
840÷76=(分钟)
答:甲从A地出发走到B地要用分钟。
根据题意,利用相遇问题公式:速度和=路程÷相遇时间,求甲乙两人速度和;利用追及问题公式:速度差=路程÷追及时间,求甲乙两人速度差;再利用和差问题公式:(和+差)÷2=大数,求甲的速度;进而求甲从A地走到B地的时间即可。
26.解:4.8×60÷4.5
=288÷4.5
=64(千克)
答:现在可以买64千克大米。
现在可以买大米的质量=原来大米的单价×购买的质量÷现在的单价。
27.解:9÷÷100000
=3600000÷100000
=36(千米)
36÷2÷(5+4)×5
=36÷2÷9×5
=18÷9×5
=2×5
=10(千米/时)
答:客车的速度是10千米/时。
客车的速度=甲,乙两地的路程÷相遇时间÷速度总份数×客车速度占的份数;其中,甲,乙两地的路程=图上距离÷比例尺。
28.解:设客车速度为x千米/小时,
x=100
(千米)
答:甲城和乙城相距750千米。
设客车的速度是x千米,则货车的速度是x,根据等量关系式:两车的速度差×时间=50,列出方程并解方程,方程的解为客车的速度,据此求出货车的速度,再根据“路程=两车速度和×时间”求出甲城和乙城的距离。
29.解:(1)(465-305)÷2=160÷2=80(千米)答:这辆车平均每时行80千米。(2)算式“465-92”求的是青县到东岭之间的距离。465-92=373(千米)答:算式“465-92”求的是青县到东岭之间的距离,青县到东岭之前的距离是373千米。
(1)解:(465-305)÷2
=160÷2
=80(千米)
答:这辆车平均每时行80千米。
(2)解:算式“465-92”求的是青县到东岭之间的距离。
465-92=373(千米)
答:算式“465-92”求的是青县到东岭之间的距离,青县到东岭之前的距离是373千米。
(1)这辆车平均每时行驶的路程=(新城~青县的路程-新城~石河的路程)÷行驶的时间;
(2)算式“465-92”求的是青县到东岭之间的距离是373千米。
30.解:6.62×4.5+4.5×3.4-3.7
=29.79+15.3-3.7
=45.09-3.7
=41.39(元)
答:张阿姨实际支付了41.39元。
张阿姨实际支付的钱数=苹果的单价×数量+橘子的单价×数量-支付宝红包一次性抵扣的金额。
31.解:甲乙速度比是5∶4,
甲用的时间:1÷40=
×
=×
=
1÷=72(分钟)
乙用的时间:×
=×
=
1÷=90(分钟)
乙比甲要晚:90-72=18(分钟)
答:乙到达A地要比甲到达B地晚18分钟
把两地的距离看作单位“1”,所用时间的比是4:5,速度比就是5:4;根据相遇问题的基本数量关系式:速度和×相遇时间=总路程,可以求出甲乙速度和是:1÷40=;可进一步求出甲的速度:×=,乙的速度:×=,根据路程÷速度=时间,甲用的时间:1÷=72(分钟),乙用的时间:1÷=90(分钟),因此乙比甲要晚90-72=18(分钟)到达。
32.解:4.85×[60-60÷(4+1)]+2.58×[60-60÷(5+1)]+3.5×60
=4.85×[60-60÷5]+2.58×[60-60÷6]+210
=4.85×[60-12]+2.58×[60-10]+210
=4.85×48+2.58×50+210
=232.8+129+210
=361.8+210
=571.8(元)
571.8元<600元
答:老师用600元准备午餐够。
准备午餐需要的总钱数=汉堡的单价×买汉堡的数量+冰红茶的单价×买冰红茶的数量+火腿肠的单价×买火腿肠的数量,然后和600元比较大小;其中,买的数量=计划买的数量-赠送的数量。
07 数量关系
一、单选题
1.大毛骑车上学,去时每小时行18千米,回来时每小时行12千米,则大毛往返平均速度为( )千米/时.
A.108 B.14.4 C.15 D.16.2
2.“高原精灵”藏羚羊是国家一级保护动物,每年5月,藏羚羊开始一年一度的迁徙产仔之旅,它的速度达到1320米/分,藏羚羊每秒能行多少米?解决这个问题所用的数量关系是( )。
A.路程÷时间=速度 B.路程÷速度=时间 C.速度×时间=路程
3.在比例尺是1:500的图纸上,测得一块长方形的土地长5厘米,宽4厘米,这块土地的实际面积是( )平方米。
A.20 B.500 C.5000 D.50
4.某品牌免洗抑菌洗手液一瓶50元,买5瓶送1瓶,750元最多可以买( )瓶。
A.16 B.18 C.20
5.王阿姨目前使用的手机话费套餐如下:月基本话费是58元,这款套餐包含80分钟免费通话时间和20G基本流量,通话超出部分按每分钟0.19元计算,流量超出部分按10元/G计算。王阿姨12月份一共通话120分钟,使用流量18G,那么她这个月需要支付话费( )元。
A.7.6 B.65.6 C.73.2 D.80.8
6.下列运动中,奔跑速度最快的是( )。
A.狮子:6分钟8千米 B.兔子:5分钟4500米
C.斑马:1000米/分 D.马:60千米/时
7.停车场对小汽车的收费标准如下, 半小时即以内免费,半小时以上每过一小时收费八元, 不足一小时按一小时算。如果一辆汽车付停车费 24 元,那么它的停车时间段可能是( )
A.12:30~14:30 B.10:00~12:35
C.13:25~14:45 D.8:15-12:00
8.小小和妈妈沿着圆形花坛散步。小小走一圈用12分钟,妈妈走一圈用8分钟。如果两人同时同地出发,相背而行,走了16分钟后,两人的位置是下面的图( )。
A. B.
C. D.
9.甲、乙两辆垃圾清运车从垃圾处理站出发回收垃圾。两车背向而行,行驶了0.5h后,两车相距85km,甲、乙两车的速度比是8∶9,乙车比甲车每小时快( ) km。
A.15 B.12 C.10 D.20
10.小芳和小红同时从 A、B两城出发,相向而行,16小时后在途中相遇,已知小芳比小红速度快,那么小芳从A城到B城要用( )小时。
A.20 B.24 C.31 D.32
11.夜晚,奇奇和爸爸在路边散步,从第1个路灯到第19个路灯,共花了10分钟(相邻路灯间距离相等)。奇奇和爸爸的步行速度是1.2米/秒,相邻两个路灯之间的距离是( )米。
A.0.6 B.30 C.36 D.40
二、填空题
12.一辆汽车2小时行了125千米,这辆汽车所行驶路程和时间的比是 ,比值是 ,这个比值表示 。
13.张良沿一公路徒步,速度为每小时4.2千米。沿该路的公共汽车每36分钟就有一辆车从后面超过他。每12分钟就又遇到迎面开来的一辆车,如果公共汽车按相等的时间间隔,以同一速度前行,那么,公共汽车发出时间间隔是 ?
14.一辆汽车6时行驶了 540 km,路程与时间的比是 ,比值是 ,这个比值表示 。
15.在一幅比例尺为1:3000000的地图上,量得A、B两地相距12cm,则A、B两地实际相距 km。一辆货车从A地开往B地,每小时行驶80km,需要 小时才能到达。
16.为了丰富校园文体生活,提高 路程/m学生的身体素质,培养学生养成良好的锻炼习惯,让学生在体育锻炼中感受积极健康的生活,学校组织全校学生开展冬季晨跑活动。六年级学生每天晨跑的目标是600 m,上面是成成和嘟嘟跑步的路程与时间的关系图。
(1)成成跑完全程用时 分,当成成跑完全程后,嘟嘟又跑 分才跑完全程。
(2)成成跑步的路程与时间的比是 ,比值是 比值表示的是 。
17.元旦迎新会上,401 班要买40套演出服。商场正在“买4送1”活动。如果演出服120元/套,请问401班至少需要付 元。
18.商店购进一批每双6.50元的凉鞋,售价为7.40元,当卖到还到5双时,除去全部成本外还获利44元,那么这批凉鞋会共有 双。
19.家住西樵山下,年过六旬的吴大爷秋日步行锻炼,他从西樵山北门牌坊出发,每行5分钟就休息2分钟,匀速前进,步行50分钟到达终点翠岩牌坊。已知吴大爷最后一次休息时离翠岩牌坊还有70米。那么:吴大爷在途中休息用了 分钟;吴大爷步行的速度是每分钟 米。
20.一座大桥长2400米。一列火车通过大桥时每分钟行940米,从车头上桥到车尾离桥共需 3 分钟,这列火车长 米。
21.一辆汽车从甲地开往Z地,行前一半时间的速度和行后一半时间的速度之比是7:9 ,那么行前一半路程和行后一半路程的时间之比是 。
22.甲、乙两车从同一地点出发沿同一高速公路从A地到B地.甲车先出发2小时,乙车出发后经5小时与甲车同时到达B地,如果乙车时速增加8千米.那么,出发后4小时可追上甲车.A地与B地的距离是 千米。
三、解答题
23.奇奇和妙妙从圆形广场的同一地点背对背出发,5分钟后两个人相遇,妙妙步行的速度是65米/分,奇奇步行的速度是68米/分,这个圆形广场的半径约为多少米?(结果保留整数)
24.妈妈买回3千克大米和12千克大豆,共付了人民币67.5元,已知每千克大米6.5元,每千克大豆多少元?
25.已知A、B两地相距840米,甲、乙两人分别从A、B两地同时出发,相向而行,6分钟相遇,若同向而行,70分钟后甲可以追上乙,问甲从A地出发走到B地要用多少分钟?
26.某品牌大米原来的单价是每千克4.8元,活动促销价是每千克4.5元。奶奶用原价买60千克的钱,现在可以买多少千克大米?
27.在比例尺是1:400000的地图上量得甲、乙两地相距9cm,一列货车和一列客车分别从甲,乙两地同时开出,相向而行,2小时相遇,已知客车与货车的速度比是5:4,客车的速度是多少?
28.一辆客车和一辆货车同时分别从甲城、乙城相向开出,4小时后两车相遇,客车比货车多行50千米。已知货车速度是客车的速度的,求甲城和乙城相距多少千米。(用方程解答)
29.下面是“新城-青县”的长途汽车沿线各车站的汽车里程表。
新城-东岭 92千米
新城-李庄 164千米
新城-广山 212千米
新城-石河 305千米
新城-青县 465千米
(1)小王坐长途汽车从石河出发,2时后到达青县,这辆车平均每时行多少千米?
(2)算式“465-92”求的是什么?写一写,算一算。
30.张阿姨在水果店买了6.62千克苹果和4.5千克橘子,她用支付宝支付,支付宝红包一次性抵扣了3.7元,张阿姨实际支付了多少元?
31.A、B两地,甲乙两人骑自行车行驶全程所用的时间之比为4:5,如果甲乙两人分别同时从A、B两地相对行驶,40分钟后两人相遇,相遇后各自继续前行,那么乙到达A地比甲到达B地要晚多少分钟?
32. 前进小学要去秋游,有学生60人,老师为学生准备了午餐,有火腿肠、冰红茶和汉堡,每人一份。火腿肠每根3.5元,冰红茶每瓶2.58元,汉堡每个4.85元。后来老师发现商场正在搞促销,汉堡买四赠一,冰红茶买五赠一。老师用600元准备午餐够吗?
答案解析部分
1.B
解:假设家到学校的距离为1千米。
(1+1)÷(+)
=2÷
=14.4(千米/时);
故答案为:B。
假设家到学校的距离为1千米,则去时用了小时,回来用了小时,往返一共行了1+1=2(千米),用往返的总路程除以往返用的总时间即可求出往返的平均速度,据此解答。
2.A
解:用1320÷60来计算,用的数量关系是路程÷时间=速度。
故答案为:A。
速度×时假=路程,路程÷速度=时间,路程÷时间=速度,求每秒能行的长度就是求速度。
3.B
解:5÷÷100
=2500÷100
=25(米)
4÷÷100
=2000÷100
=20(米)
25×20=500(平方米)。
故答案为:B。
这块土地的实际面积=实际长×实际宽;其中,实际距离=图上距离÷比例尺,然后单位换算。
4.B
解:5+1=6(瓶)
50×5=250(元)
750÷250=3(组)
3×6=18(瓶)。
故答案为:B。
买5瓶送1瓶,因此可以把6瓶洗手液看作一组,一组的总价=单价×5瓶,组数=总价÷平均每组的钱数,最后再乘6即可。
5.B
解:(120-80)×0.19+58
=40×0.19+58
=7.6+58
=65.6(元)
故答案为:B。
通话时长超出80分钟,要加收费用。流量使用少于20G,不需要加收费用。用120减去80求出超出的时间,用超出的时间乘0.19求出超出80分钟的费用,再加上基本话费即可求出这个月需要支付的话费。
6.A
解:8000÷6=1333(米)……2(米)
4500÷5=900(米)
1时=60分钟
60000÷60=1000(米)
1333>1000>900
狮子的速度最快。
故答案为:A。
速度=路程÷时间,先单位换算,分别计算出平均每分钟跑的米数,然后再比较大小。
7.B
解:24÷8+0.5
=3+0.5
=3.5(小时)。
A项:14时30分-12时30分=2小时,不符合题意。
B项:12时35分-10时=2小时35分,不足一小时按一小时算,所以该停车时长为3小时,符合题意。
C项:14时45分-13时25分=1小时20分,不足一小时按一小时算,所以该停车时长为2小时,不符合题意。
D项:12时-8时15分=3小时45分,根据题目的要求,不足一小时按一小时算,所以该停车时长为4小时,不符合题意。
故答案为:B。
此题考查的是对时间段和收费标准的理解与应用。首先根据题目的要求,确定24元停车费对应的实际停车时长。然后,分别计算出四个选项的停车时长,注意将不足一小时的时间段按一小时计费。最后,比较四个选项的停车时长与实际时长,找出符合题意的选项。
8.C
解:16÷12=1(圈)······4(分钟)
16÷8=2(圈), 能表示两人的位置。
故答案为:C。
走了16分钟后,小小走了1圈加上一圈的处,妈妈刚好走2圈,据此选择。
9.C
甲车1小时行驶的路程:85×÷0.5=80(千米)
乙车1小时行驶的路程:85×÷0.5=90(千米)
90-80=10(千米)
故答案为:C
先分别用两车行驶的路程乘两车各自行驶路程占总路程的分率,求出甲、乙两车0.5小时各行驶的路程,再除以0.5求出每小时各行驶的路程,再相减即可。
10.C
设小红的速度为v,则小芳的速度为v+v= v ,两人的速度和是v+v=v,根据路程=速度和×相遇时间可知,A、B两城之间的距离为v×16,用两城之间的距离除以小芳的速度,即为小芳从A城到B城所需要的时间,列式计算为:v×16÷v=×15=31(小时)。
故答案为:C
解决此题的关键是根据小芳比小红速度快,用含有字母的式子表示出小红和小芳的速度,再根据相遇的时间用含有字母的式子表示出A、B两城之间的距离,最后用两城之间的距离除以小芳的速度,即可求出小芳从A城到B城要用的时间。
11.D
解:1.2×10×60=720(米),720÷(19-1)=40(米),
故答案为:D
本题属于两端都栽的植树问题,所以间隔数=棵数-1,根据路程=速度×时间计算出从第1个路灯到第19个路灯的总长度,用总长度÷间隔数即可知道相邻两个路灯之间的距离.
12.125:2;;汽车每小时行驶的速度
解:路程∶时间=125∶2;比值是125∶2=;这个比值表示:这辆汽车每小时行驶的路程。
故答案为:125∶2;;汽车每小时行驶的速度。
比是由一个前项和一个后项组成的除法算式,只不过把“÷”(除号)改成了":"(比号)而已,但除法算式表示的是一种运算,而比则表示两个数的关系。比值: 比的前项除以比的后项所得到的数。
13.18
解:设汽车速度为每小时x千米。
36分= 0.6小时12分=0.2小时
0.6(x - 4.2) = 0.2(x+4.2)
解得:x=8.4
汽车与张良的速度差为:8.4-4.2=4.2(千米/时)
发车间隔为:4.2 x0.6÷8.4= 2.52÷8.4=0.3(小时),0.3小时= 18分钟
故答案为:18。
根据题意,先求出汽车与张良的速度差和速度和,再根据和差公式求出汽车的速度,再根据追及问题求出追及路程,用追及路程除以汽车的速度,就是汽车发车的间隔时间。
14.90:1;90;这辆汽车的平均速度
解:汽车所行驶的路程和时间的比:540∶6=(540÷6)∶(6÷6)=90∶1
比值:90÷1=90
比值表示:汽车每小时行驶的路程,即速度。
故答案为:90:1;90;这辆汽车的平均速度
根据题意,求汽车行驶的路程和时间的比,也就是求540和6的比,然后根据比的性质进行化简;比的前项除以比的后项,求出的商就是比值,路程÷时间=速度,据此解答。
15.360;4.5
解:12÷÷100000
=36000000÷100000
=360(千米)
360÷80=4.5(小时)。
故答案为:360;4.5。
实际距离=图上距离÷比例尺;然后单位换算;到达需要的时间=路程÷速度。
16.(1)4;1
(2)150:1;150;速度
解:(1)根据题图,成成跑完全程用时4分;
5-4=1(分)
当成成跑完全程后,嘟嘟又跑1分才跑完全程。
(2)600:4=150:1=150
这个比值表示的是速度。
故答案为:4;1;150:1;150;速度。
(1)根据题图可以分别找到成成和嘟嘟跑步的时间。
(2)从图中可以找到成成跑步的路程和时间,两数相比并求值即可;速度=路程÷时间,比值表示的是时间。
17.3840元
解:40÷(4+1)
=40÷5
=8(组)
8×4×120=3840(元)
故答案为:3840。
“买4送1”表示花4套的价钱买5套,先求出40里面有几个5,那么需要付的钱数=几×4×一套演出服的价钱,据此代入数值作答即可。
18.90
解:设这批凉鞋共有x双。
7.40(x-5)- 6.50x = 44
7.4x-37-6.5x=44
0.9x=81
x=90
故答案为:90
设这批凉鞋共有x双,先计算购进凉鞋的总成本=单价×数量,即6.50x双;再计算售出凉鞋的总收入=单价×数量,即7.40(x-5)双;因售出凉鞋的总收入比购进凉鞋的总成本多44元,所以可以列出关于x的方程:7.40(x-5)- 6.50x = 44,解方程即可求出答案。
19.14;70
解:50÷(5+2)
=50÷7
=7(次)······1(分)
休息:7×2=14(分)
步行:50-14=36(分)
速度:70÷1=70(米/分)。
故答案为:14;70。
先用总时间÷每次周期的时间=周期数······余下的时间,则最后一分钟仍然在步行,所以步行时间是36分,休息时间是14分钟,最后一次休息时离翠岩牌坊还有70米,则这70米步行用了1分钟,所以速度是70米/分。
20.420
解:如图:
940×3-2400
=2820-2400
=420(米)
这列火车长420米
故答案为:420。
火车长+桥长=火车行驶的路程,据此推出:火车长=火车行驶的路程-桥长。
21.5:4
解:设一半时间为“1”,则总路程是:
1×7+1×9
=7+9
=16
前一半路程为:16÷2=8
用时为:(8-1×7)÷9+1
=1÷9+1
=
后一半路程用时为:16÷2÷9
=8÷9
=
时间比是为::=10:9=5:4。
故答案为:5:4。
“对半”行程问题,设一半时间为“1”,然后求出总路程,再将总路程平分,则一半路程为:16÷2=8,前一半时间所行路程为7,则前一半路程的时间为,进而求出后一半路程所用时间,写出比后,依据比的基本性质化简比。
22.560
解:甲与乙的速度比为5∶(2+5)=5∶7
故设甲的速度为5v千米/小时,乙的速度为7x千米/小时。
4×(7v+8)=(4+2)×5v
28v+32=30v
2v=32
v=16
5×16×7=560(千米)
故答案为:560。
根据“甲车先出发2小时,乙车出发后经5小时与甲车同时到达B地”可知甲乙两车走相同路程(AB两地的距离),用时为5+2=7、5小时,则他们的速度比为5:7,由此可设出甲的速度为5v千米/小时,乙的速度为7v千米/小时;之后根据“如果乙车时速增加8千米,那么,出发后4小时可追上甲车”便可列出一方程4×(7v+8)=(4+2)×5v,求得v的值,即可得到甲、乙的速度,之后就可据“速度×时间=距离”得出问题答案。
23.解:(65+68)×5
=133×5
=665(m)
665÷3.14÷2≈106(m)
答:这个圆形广场的半径约为 106 m。
“奇奇和妙妙从圆形广场的同一地点背对背出发,5分钟后两个人相遇 ”,即5分钟两人走的路程,就是圆形广场的周长。“ 妙妙步行的速度是65米/分,奇奇步行的速度是68米/分 ”,所以5分钟两人的路程合计为(65+68)×5=665(m),因此圆形广场的周长也是665m。根据公式“圆周长=2πr”,因此圆形广场的半径就是665÷3.14÷2≈106(m)。
24.解:(67.5-6.5×3)÷12
=(67.5-19.5)÷12
=48÷12
=4(元)
答:每千克大豆4元。
每千克大米的钱数×3=3千克大米的钱数,总钱数-3千克大米的钱数=买大豆花的钱数,买大豆花的钱数÷大豆买的质量=大豆的单价。
25.解:速度和:840÷6=140(米/分),
速度差:840÷70=12(米/分),
甲:(140+12)÷2=76(米/分)
840÷76=(分钟)
答:甲从A地出发走到B地要用分钟。
根据题意,利用相遇问题公式:速度和=路程÷相遇时间,求甲乙两人速度和;利用追及问题公式:速度差=路程÷追及时间,求甲乙两人速度差;再利用和差问题公式:(和+差)÷2=大数,求甲的速度;进而求甲从A地走到B地的时间即可。
26.解:4.8×60÷4.5
=288÷4.5
=64(千克)
答:现在可以买64千克大米。
现在可以买大米的质量=原来大米的单价×购买的质量÷现在的单价。
27.解:9÷÷100000
=3600000÷100000
=36(千米)
36÷2÷(5+4)×5
=36÷2÷9×5
=18÷9×5
=2×5
=10(千米/时)
答:客车的速度是10千米/时。
客车的速度=甲,乙两地的路程÷相遇时间÷速度总份数×客车速度占的份数;其中,甲,乙两地的路程=图上距离÷比例尺。
28.解:设客车速度为x千米/小时,
x=100
(千米)
答:甲城和乙城相距750千米。
设客车的速度是x千米,则货车的速度是x,根据等量关系式:两车的速度差×时间=50,列出方程并解方程,方程的解为客车的速度,据此求出货车的速度,再根据“路程=两车速度和×时间”求出甲城和乙城的距离。
29.解:(1)(465-305)÷2=160÷2=80(千米)答:这辆车平均每时行80千米。(2)算式“465-92”求的是青县到东岭之间的距离。465-92=373(千米)答:算式“465-92”求的是青县到东岭之间的距离,青县到东岭之前的距离是373千米。
(1)解:(465-305)÷2
=160÷2
=80(千米)
答:这辆车平均每时行80千米。
(2)解:算式“465-92”求的是青县到东岭之间的距离。
465-92=373(千米)
答:算式“465-92”求的是青县到东岭之间的距离,青县到东岭之前的距离是373千米。
(1)这辆车平均每时行驶的路程=(新城~青县的路程-新城~石河的路程)÷行驶的时间;
(2)算式“465-92”求的是青县到东岭之间的距离是373千米。
30.解:6.62×4.5+4.5×3.4-3.7
=29.79+15.3-3.7
=45.09-3.7
=41.39(元)
答:张阿姨实际支付了41.39元。
张阿姨实际支付的钱数=苹果的单价×数量+橘子的单价×数量-支付宝红包一次性抵扣的金额。
31.解:甲乙速度比是5∶4,
甲用的时间:1÷40=
×
=×
=
1÷=72(分钟)
乙用的时间:×
=×
=
1÷=90(分钟)
乙比甲要晚:90-72=18(分钟)
答:乙到达A地要比甲到达B地晚18分钟
把两地的距离看作单位“1”,所用时间的比是4:5,速度比就是5:4;根据相遇问题的基本数量关系式:速度和×相遇时间=总路程,可以求出甲乙速度和是:1÷40=;可进一步求出甲的速度:×=,乙的速度:×=,根据路程÷速度=时间,甲用的时间:1÷=72(分钟),乙用的时间:1÷=90(分钟),因此乙比甲要晚90-72=18(分钟)到达。
32.解:4.85×[60-60÷(4+1)]+2.58×[60-60÷(5+1)]+3.5×60
=4.85×[60-60÷5]+2.58×[60-60÷6]+210
=4.85×[60-12]+2.58×[60-10]+210
=4.85×48+2.58×50+210
=232.8+129+210
=361.8+210
=571.8(元)
571.8元<600元
答:老师用600元准备午餐够。
准备午餐需要的总钱数=汉堡的单价×买汉堡的数量+冰红茶的单价×买冰红茶的数量+火腿肠的单价×买火腿肠的数量,然后和600元比较大小;其中,买的数量=计划买的数量-赠送的数量。
同课章节目录
