3.2.1 不等式的基本性质 课件(共22张PPT)
文档属性
| 名称 | 3.2.1 不等式的基本性质 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 409.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
不等式的基本性质
七年级下册 第三章 3.2.1
学习目标
1.经历通过类比、猜测、验证发现不等式性质的探索过程。
2.掌握不等式的基本性质,并能初步运用不等式的基本性质比较大小。
3.通过探究不等式的基本性质,培养逻辑推理能力。
4.在纠错与反思中培养细致、规范的运算习惯。
新课导入
小红今年11岁,小明今年13岁,你可以用不等号来表示他们年龄之间的关系吗?
11<13
5年后,小红和小明谁更大?
11+5<13+5
10年后,小红和小明谁更大?
11+5<13+5
5年前,小红和小明谁更大?
11-5<13-5
n年前,小红和小明谁更大?
11-n<13-n
n年后,小红和小明谁更大?
11+n<13+n
新知探究
如果a,b,c都是实数,且a不等式的基本性质1
猜测: a+c思考:你能证明该猜测吗?
1.作差法
2.数轴法
新知探究
已知: a,b,c都是实数,且a求证: a+c作差法
证明:若a∵ (a+c)(b+c)= a+cbc=ab<0,
∴ a+c∵ (ac)(bc)= acbc=ab<0,
∴ ac新知探究
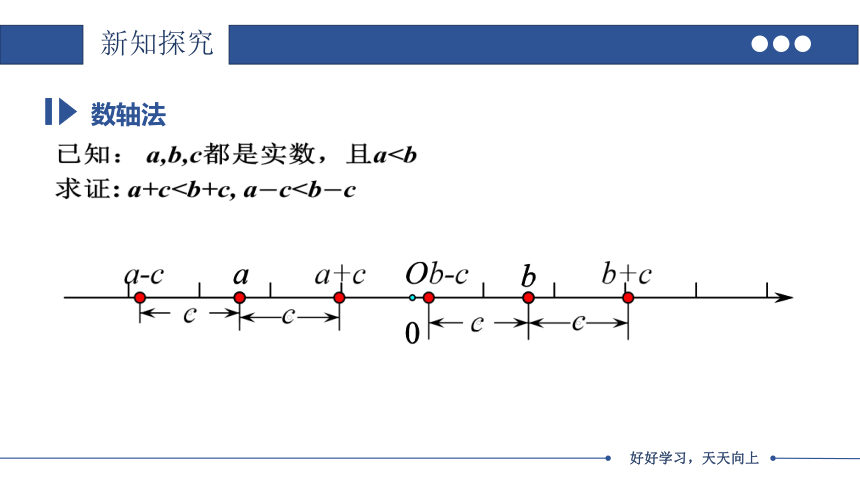
已知: a,b,c都是实数,且a求证: a+c数轴法
新知探究
不等式的两边都加上或减去同一个数(或同一个整式),不等号的方向不变.
不等式的基本性质1
如果a例1 用“>”或“<”填空:
(1)已知a>b,则a+ b+;
(2)已知3<7,则3x 7x.
例题探究
>
<
新知探究
已知3<5,先用“>”或“<”填空:
3×2____5×2, 3×π_____5×π , _____ , _____ 。
再观察结果,由此可猜测出什么结论
做一做
<
<
<
<
不等式俩边同时乘或除以同一个正数,不等号的方向不变.
新知探究
不等式的基本性质2
思考:如果a,b,c都是实数,且a>b,c>0,那么ac和bc的大小关系是什么? 和的大小关系是什么?你能证明它吗?
ac>bc, >
新知探究
已知: a,b,c都是实数,且a>b,c>0
求证: ac>bc, >
证明:若a>b,c>0则ab>0,>0
∵ c>0
∴ ac-bc=c(a-b)>0(同号得正)
∴ ac>bc
新知探究
已知: a,b,c都是实数,且a>b,c>0
求证: ac>bc, >
证明:∵>0
∴ =(a-b)>0 (同号得正)
∴ >
新知探究
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
不等式的基本性质2
如果a>b,c>0 ,则ac>bc, >
例2 用 “>”或“<” 填空:
(1)已知a<b,则a b;
(2)已知a>b,则 .
例题探究
>
<
例3 利用 >2,比较与的大小.
例题探究
解:∵>2,
∴ >2(不等式的基本性质1)
∴ >
∵2>0
∴ (不等式的基本性质2)
课堂小结
不等式的两边都加上或减去同一个数(或同一个整式),不等号的方向不变.
不等式的基本性质1
如果a不等式的基本性质2
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0 ,则ac>bc, >
课堂练习
1.下列变形一定正确的是 ( )
由x>y,得x+a>y+b
B. 由x>y,得x-3>y+3
C. 由x>y,得x-a>y-b
D. 由x>y,得x+2>y+2
D
课堂练习
2.若a>b,则下列不等式变形正确的是( )
A.a+5B.>
C.a-4D.3a-2<3b-2
B
课堂练习
3.若m>n,则下列不等式中,不成立的是 ( )
3m>3n
B. m>n
C. m>n
D. 4n>4m
D
课堂练习
4.若3x>-3y,则下列不等式中一定成立的是 ( )
A. x+y>0
B. x-y>0
C. x+y<0
D. x-y<0
A
课后作业
课堂作业:P61 T1-3
家庭作业:《学法》P37-38 A组(基础一般)
B组(基础较好)
C组(选做)
不等式的基本性质
七年级下册 第三章 3.2.1
学习目标
1.经历通过类比、猜测、验证发现不等式性质的探索过程。
2.掌握不等式的基本性质,并能初步运用不等式的基本性质比较大小。
3.通过探究不等式的基本性质,培养逻辑推理能力。
4.在纠错与反思中培养细致、规范的运算习惯。
新课导入
小红今年11岁,小明今年13岁,你可以用不等号来表示他们年龄之间的关系吗?
11<13
5年后,小红和小明谁更大?
11+5<13+5
10年后,小红和小明谁更大?
11+5<13+5
5年前,小红和小明谁更大?
11-5<13-5
n年前,小红和小明谁更大?
11-n<13-n
n年后,小红和小明谁更大?
11+n<13+n
新知探究
如果a,b,c都是实数,且a
猜测: a+c
1.作差法
2.数轴法
新知探究
已知: a,b,c都是实数,且a
证明:若a
∴ a+c
∴ ac
已知: a,b,c都是实数,且a
新知探究
不等式的两边都加上或减去同一个数(或同一个整式),不等号的方向不变.
不等式的基本性质1
如果a
(1)已知a>b,则a+ b+;
(2)已知3<7,则3x 7x.
例题探究
>
<
新知探究
已知3<5,先用“>”或“<”填空:
3×2____5×2, 3×π_____5×π , _____ , _____ 。
再观察结果,由此可猜测出什么结论
做一做
<
<
<
<
不等式俩边同时乘或除以同一个正数,不等号的方向不变.
新知探究
不等式的基本性质2
思考:如果a,b,c都是实数,且a>b,c>0,那么ac和bc的大小关系是什么? 和的大小关系是什么?你能证明它吗?
ac>bc, >
新知探究
已知: a,b,c都是实数,且a>b,c>0
求证: ac>bc, >
证明:若a>b,c>0则ab>0,>0
∵ c>0
∴ ac-bc=c(a-b)>0(同号得正)
∴ ac>bc
新知探究
已知: a,b,c都是实数,且a>b,c>0
求证: ac>bc, >
证明:∵>0
∴ =(a-b)>0 (同号得正)
∴ >
新知探究
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
不等式的基本性质2
如果a>b,c>0 ,则ac>bc, >
例2 用 “>”或“<” 填空:
(1)已知a<b,则a b;
(2)已知a>b,则 .
例题探究
>
<
例3 利用 >2,比较与的大小.
例题探究
解:∵>2,
∴ >2(不等式的基本性质1)
∴ >
∵2>0
∴ (不等式的基本性质2)
课堂小结
不等式的两边都加上或减去同一个数(或同一个整式),不等号的方向不变.
不等式的基本性质1
如果a
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0 ,则ac>bc, >
课堂练习
1.下列变形一定正确的是 ( )
由x>y,得x+a>y+b
B. 由x>y,得x-3>y+3
C. 由x>y,得x-a>y-b
D. 由x>y,得x+2>y+2
D
课堂练习
2.若a>b,则下列不等式变形正确的是( )
A.a+5
C.a-4
B
课堂练习
3.若m>n,则下列不等式中,不成立的是 ( )
3m>3n
B. m>n
C. m>n
D. 4n>4m
D
课堂练习
4.若3x>-3y,则下列不等式中一定成立的是 ( )
A. x+y>0
B. x-y>0
C. x+y<0
D. x-y<0
A
课后作业
课堂作业:P61 T1-3
家庭作业:《学法》P37-38 A组(基础一般)
B组(基础较好)
C组(选做)
同课章节目录
