2024-2025学年苏科版数学八下 9.4矩形、菱形、正方形 同步练习(含答案)
文档属性
| 名称 | 2024-2025学年苏科版数学八下 9.4矩形、菱形、正方形 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 234.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 07:51:46 | ||
图片预览

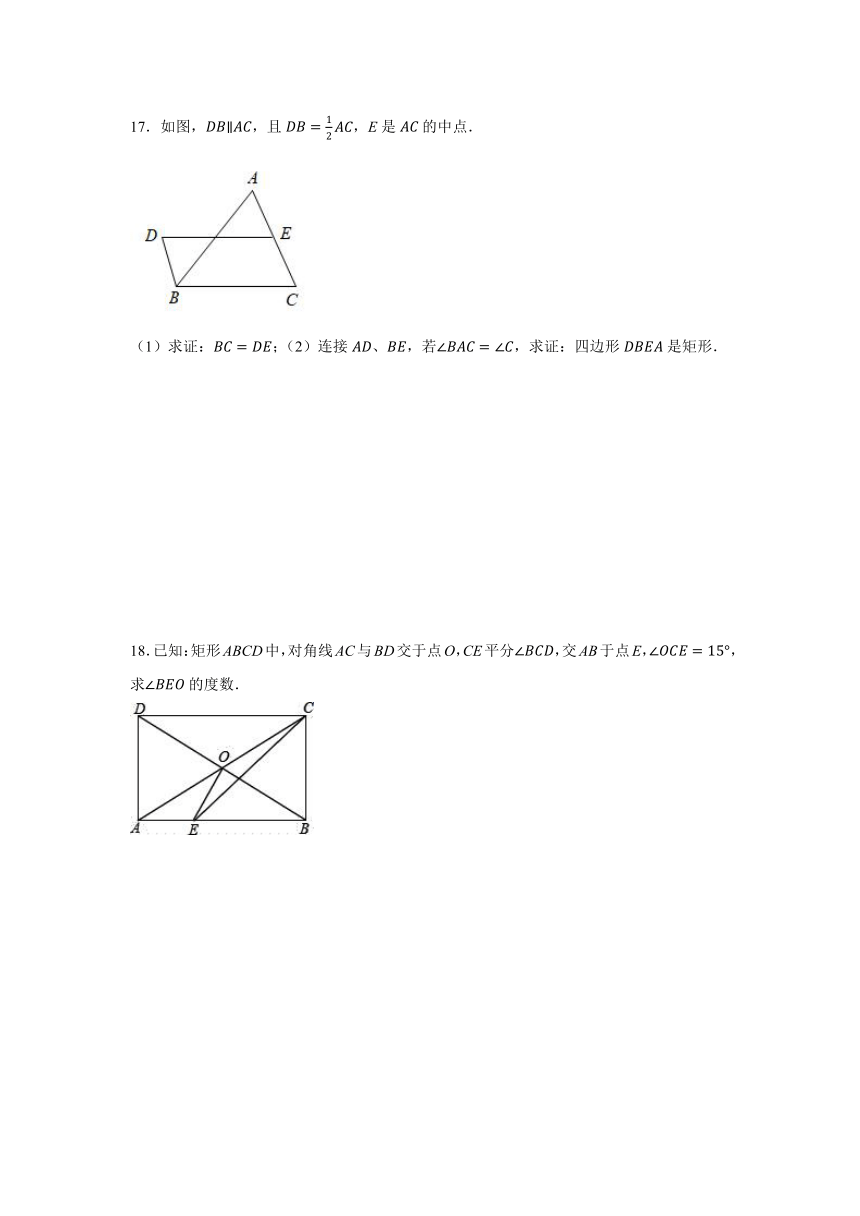
文档简介
2024-2025学年苏科版数学八下 9.4矩形、菱形、正方形 同步练习
一、单选题
1.小明想判断家里的门框是否为矩形,他应该( )
A.测量三个角是否都是直角 B.测量对角线是否互相平分
C.测量两组对边是否分别相等 D.测量一组对角是否是直角
2.已知四边形是平行四边形,下列说法正确的是( )
A.当时,四边形是矩形
B.时,四边形是菱形
C.当时,四边形是菱形
D.当时,四边形是正方形
3.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
4.如图,正方形的顶点,的坐标分别是,,则顶点的坐标是( )
A. B. C. D.
5.如图,四边形是菱形,对角线,,于点,则的长为( )
A. B. C. D.
6.如图,在菱形中,对角线,相交于点,,,则下列选项错误的是( )
A. B. C. D.
7.如图,P为矩形外一点,,则的面积是( )
A.3 B.4 C.1.5 D.2.5
8.如图是一张长方形纸片,点M是对角线的中点,点E在边上,把沿直线折叠,使点C落在对角线AC上的点F处,连接.若,则的度数为( )
A.15° B.16° C.18° D.20°
二、填空题
9.正方形一条对角线为2,则正方形的面积为 .
10.如图,在菱形ABCD中,点P是对角线AC上的一点,PE⊥AB于点E.若PE=3,则点P到AD的距离为 .
11.如图,菱形的一条对角线上一点O,到菱形一边的距离为2,那么点O到另外一边的距离为________.
12.如图,点E是矩形中边上一点,将沿折叠为,点F落在边上,若,则 .
13.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为 度.
14.如图所示,正方形的边长为4,以为边作等边三角形,,若正方形的对角线上有一动点M,则周长的最小值是 .
三、解答题
15.如图,在菱形ABCD中,∠ABC=120°,对角线AC,BD相交于点O,AE平分∠CAD,分别交OD,CD于F,E两点,求∠AFO的度数.
16.如图,将矩形纸片折叠,使点B与点D重合,点A落在点P处,折痕为.
(1)求证:;
(2)若,求的长.
17.如图,,且,E是的中点.
(1)求证:;(2)连接、,若,求证:四边形是矩形.
18.已知:矩形ABCD中,对角线AC与BD交于点O,CE平分,交AB于点E,,求的度数.
19.如图,点,分别在正方形的边,上,且,把绕点顺时针旋转得到.
(1)求证:≌.
(2)若,,求正方形的边长.
20.如图,在中,点O是边上一个动点,过点O作直线.设交的平分线于点E,交的外角的平分线于点F.
(1)求证:;
(2)若,,求的长;
(3)连接,,当点在边上运动到什么位置时,四边形是矩形?请说明理由.
参考答案
1.A
2.B
3.B
4.C
5.B
6.C
7.A
8.C
9.2
10.3
11.2
12.
13.15
14.
15.∵在菱形ABCD中,∠ABC=120°,
∴∠BAD=60°,
∵对角线AC、BD交于点O,
∴∠BAC=∠CAD=30°,∠DOA=90°
∵AE平分∠CAD,
∴∠OAF=15°,
∴∠AFO的度数为:90°-15°=75°.
16.(1)∵四边形ABCD是矩形,
∴AB=CD,∠A=∠B=∠ADC=∠C=90°,
由折叠知,AB=PD,∠A=∠P,∠B=∠PDF=90°,
∴PD=CD,∠P=∠C,∠PDF =∠ADC,
∴∠PDF-∠EDF=∠ADC-∠EDF,
∴∠PDE=∠CDF,
在△PDE和△CDF中,
,
∴(ASA);
(2)如图,过点E作EG⊥BC交于点G,
∵四边形ABCD是矩形,
∴AB=CD=EG=4cm,
又∵EF=5cm,∴cm,
设AE=xcm,
∴EP=xcm,
由知,EP=CF=xcm,
∴DE=GC=GF+FC=3+x,
在Rt△PED中,,
即,
解得,,
∴BC=BG+GC= (cm).
17.(1)∵E是的中点,
∴,
∵,
∴,
又∵,即
∴四边形是平行四边形,
∴.
(2)连接、,
∵,E是的中点,
∴,且,
∴四边形是平行四边形,
∵,
∴是等腰三角形,
∴,
由(1)知
∴,即平行四边形的对角线相等,
∴四边形是矩形.
18.∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,OA=OB=OC=OD,CD∥AB,
∵CE平分,
∴∠BCE=∠DCE=45°,
∵CD∥AB,
∴∠BEC=∠BCE=∠DCE=45°,
∴BC=BE,
∵,
∴∠BAC=30°,
∴∠ACB=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OB=BE,
∵∠EBO=∠BAC=30°,
∴∠BEO=,
19.(1)由旋转的性质得:
四边形ABCD是正方形
,即
,即
在和中,
;
(2)设正方形的边长为x,则
由旋转的性质得:
由(1)已证:
又四边形ABCD是正方形
则在中,,即
解得或(不符题意,舍去)
故正方形的边长为6.
20.(1)证明:平分,
,
,
,
,
,
同理可得,
;
(2)解:、分别平分和,
,,
,
,
,
即的长为6.5;
(3)解:当在的中点时,四边形是矩形,理由如下:
当为中点时,则,
由(1)可知,,
,
四边形为平行四边形,,
,
平行四边形为矩形.
一、单选题
1.小明想判断家里的门框是否为矩形,他应该( )
A.测量三个角是否都是直角 B.测量对角线是否互相平分
C.测量两组对边是否分别相等 D.测量一组对角是否是直角
2.已知四边形是平行四边形,下列说法正确的是( )
A.当时,四边形是矩形
B.时,四边形是菱形
C.当时,四边形是菱形
D.当时,四边形是正方形
3.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A.75° B.60° C.55° D.45°
4.如图,正方形的顶点,的坐标分别是,,则顶点的坐标是( )
A. B. C. D.
5.如图,四边形是菱形,对角线,,于点,则的长为( )
A. B. C. D.
6.如图,在菱形中,对角线,相交于点,,,则下列选项错误的是( )
A. B. C. D.
7.如图,P为矩形外一点,,则的面积是( )
A.3 B.4 C.1.5 D.2.5
8.如图是一张长方形纸片,点M是对角线的中点,点E在边上,把沿直线折叠,使点C落在对角线AC上的点F处,连接.若,则的度数为( )
A.15° B.16° C.18° D.20°
二、填空题
9.正方形一条对角线为2,则正方形的面积为 .
10.如图,在菱形ABCD中,点P是对角线AC上的一点,PE⊥AB于点E.若PE=3,则点P到AD的距离为 .
11.如图,菱形的一条对角线上一点O,到菱形一边的距离为2,那么点O到另外一边的距离为________.
12.如图,点E是矩形中边上一点,将沿折叠为,点F落在边上,若,则 .
13.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为 度.
14.如图所示,正方形的边长为4,以为边作等边三角形,,若正方形的对角线上有一动点M,则周长的最小值是 .
三、解答题
15.如图,在菱形ABCD中,∠ABC=120°,对角线AC,BD相交于点O,AE平分∠CAD,分别交OD,CD于F,E两点,求∠AFO的度数.
16.如图,将矩形纸片折叠,使点B与点D重合,点A落在点P处,折痕为.
(1)求证:;
(2)若,求的长.
17.如图,,且,E是的中点.
(1)求证:;(2)连接、,若,求证:四边形是矩形.
18.已知:矩形ABCD中,对角线AC与BD交于点O,CE平分,交AB于点E,,求的度数.
19.如图,点,分别在正方形的边,上,且,把绕点顺时针旋转得到.
(1)求证:≌.
(2)若,,求正方形的边长.
20.如图,在中,点O是边上一个动点,过点O作直线.设交的平分线于点E,交的外角的平分线于点F.
(1)求证:;
(2)若,,求的长;
(3)连接,,当点在边上运动到什么位置时,四边形是矩形?请说明理由.
参考答案
1.A
2.B
3.B
4.C
5.B
6.C
7.A
8.C
9.2
10.3
11.2
12.
13.15
14.
15.∵在菱形ABCD中,∠ABC=120°,
∴∠BAD=60°,
∵对角线AC、BD交于点O,
∴∠BAC=∠CAD=30°,∠DOA=90°
∵AE平分∠CAD,
∴∠OAF=15°,
∴∠AFO的度数为:90°-15°=75°.
16.(1)∵四边形ABCD是矩形,
∴AB=CD,∠A=∠B=∠ADC=∠C=90°,
由折叠知,AB=PD,∠A=∠P,∠B=∠PDF=90°,
∴PD=CD,∠P=∠C,∠PDF =∠ADC,
∴∠PDF-∠EDF=∠ADC-∠EDF,
∴∠PDE=∠CDF,
在△PDE和△CDF中,
,
∴(ASA);
(2)如图,过点E作EG⊥BC交于点G,
∵四边形ABCD是矩形,
∴AB=CD=EG=4cm,
又∵EF=5cm,∴cm,
设AE=xcm,
∴EP=xcm,
由知,EP=CF=xcm,
∴DE=GC=GF+FC=3+x,
在Rt△PED中,,
即,
解得,,
∴BC=BG+GC= (cm).
17.(1)∵E是的中点,
∴,
∵,
∴,
又∵,即
∴四边形是平行四边形,
∴.
(2)连接、,
∵,E是的中点,
∴,且,
∴四边形是平行四边形,
∵,
∴是等腰三角形,
∴,
由(1)知
∴,即平行四边形的对角线相等,
∴四边形是矩形.
18.∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,OA=OB=OC=OD,CD∥AB,
∵CE平分,
∴∠BCE=∠DCE=45°,
∵CD∥AB,
∴∠BEC=∠BCE=∠DCE=45°,
∴BC=BE,
∵,
∴∠BAC=30°,
∴∠ACB=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OB=BE,
∵∠EBO=∠BAC=30°,
∴∠BEO=,
19.(1)由旋转的性质得:
四边形ABCD是正方形
,即
,即
在和中,
;
(2)设正方形的边长为x,则
由旋转的性质得:
由(1)已证:
又四边形ABCD是正方形
则在中,,即
解得或(不符题意,舍去)
故正方形的边长为6.
20.(1)证明:平分,
,
,
,
,
,
同理可得,
;
(2)解:、分别平分和,
,,
,
,
,
即的长为6.5;
(3)解:当在的中点时,四边形是矩形,理由如下:
当为中点时,则,
由(1)可知,,
,
四边形为平行四边形,,
,
平行四边形为矩形.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
