8.1.1同底数幂的乘法 课件(共23张PPT)沪科版数学七年级下册
文档属性
| 名称 | 8.1.1同底数幂的乘法 课件(共23张PPT)沪科版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 12.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 19:56:43 | ||
图片预览






文档简介
(共23张PPT)
第八章 整式乘法与因式分解 8.1.1 幂的运算
同底数幂的乘法
沪科版(2024)七年级下册数学课件
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 什么叫乘方?
求几个相同因数的积的运算叫作乘方.
2. 25 表示什么?
2×2×2×2×2
3. 10×10×10×10×10 可以写成什么形式?
105
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. (-2)×(-2) ×(-2) = (-2)( )
2. a·a·a·a·a = a ( )
3. x4 = ( )
4. (-2)7 = -( )7 (-3)8 = ( )8
做 一 做
3
5
x · x · x · x
2
3
新课讲解
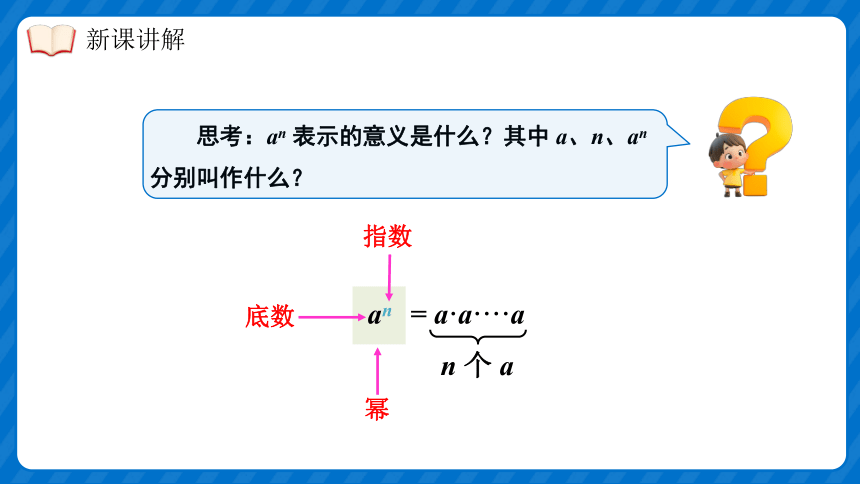
思考:an 表示的意义是什么?其中 a、n、an 分别叫作什么?
an
指数
幂
底数
= a·a····a
n 个 a
新课讲解
例题 中国设计并制造的“神威·太湖之光”是世界上首台峰值性能超过每秒 10 亿亿次的超级计算机. 峰值运算性能高达 1.25×1017 次/s,它工作 1 h(3.6×103 s)可进行多少次运算?
(1.25×1017)×(3.6×103)
=1.25×3.6×1017×103
=?
新课讲解
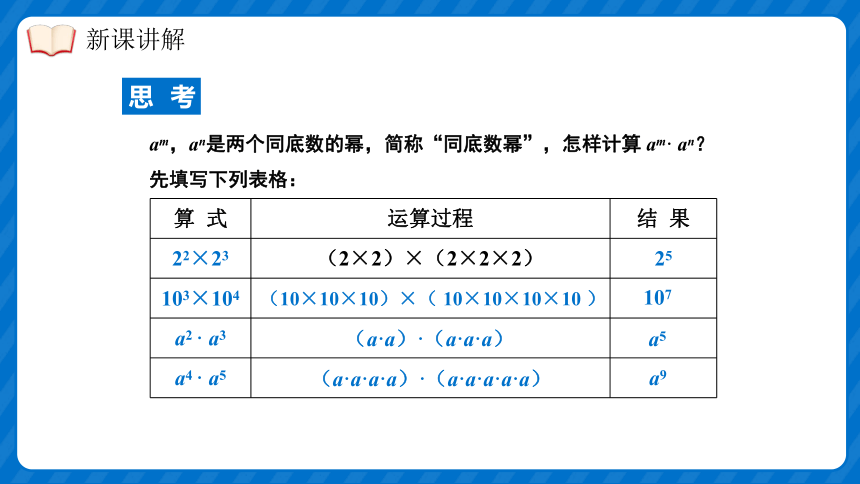
算 式 运算过程 结 果
22×23 (2×2)×(2×2×2) 25
103×104
a2 · a3
a4 · a5
am,an是两个同底数的幂,简称“同底数幂”,怎样计算 am· an?
先填写下列表格:
思 考
(10×10×10)×( 10×10×10×10 )
107
(a·a)·(a·a·a)
(a·a·a·a)·(a·a·a·a·a)
a9
a5
新课讲解
算 式 结 果
22×23 25
103×104
a2 · a3
a4 · a5
107
a9
a5
观察下表,同底数幂相乘有什么规律?
底数不变
指数相加
猜想: am · an=
(当m、n都是正整数)
新课讲解
am · an =
= a · a · … · a
(m+n)个
= am+n
一般地,如果 m,n 都是正整数,那么
( a · a · … · a )
( a · a · … · a )
m个
n个
·
新课讲解
由此得幂的运算性质 1:
am · an = am+n(m,n 都是正整数).
同底数幂相乘,底数不变,指数相加.
新课讲解
思考 当三个或三个以上同底数幂相乘时,是否也具有这一性质呢? 怎样用公式表示?
如 am · an · ap =
am+n+p
(m、n、p都是正整数)
新课讲解
计算:
例 1
(1) ;
(2)(-2)2×(-2)7;
(2)(-2)2×(-2)7 = (-2)2+7 = (-2)9 = -29.
新课讲解
计算:
(3)a2 · a3 · a6;
(4)(-y)3 · y4.
(3)a2 · a3 · a6 = a2+3+6 = a11.
(4)(-y)3 · y4 = (-y3)·y4 = -(y3·y4) = -y3+4 = -y7.
新课讲解
例 1
练 习
1. 下面的计算是否正确?为什么?
(1)x3 + x3 = x6.
(2)x3 · x3 = 2x3.
(3)c · c3 = c3.
(4)c + c3 = c4.
( )
( )
( )
( )
×
2x3
×
x6
×
c4
×
c(c2+1)
课堂练习
2. 计算:
(1)105 × 103; (2)-a2 · a5 ;
(3)-x3 · x5; (4) y8 · (-y);
(5)(-x)2 · x3 · (-x)3; (6)(-y)2 · (-y)3 · (-y).
解:(1)105 × 103 = 105+3 = 108;
(2)-a2 · a5 = -a2+5 = -a7;
(3)-x3 · x5 = -x3+5 = -x8;
课堂练习
2. 计算:
(1)105 × 103; (2)-a2 · a5 ;
(3)-x3 · x5; (4) y8 · (-y);
(5)(-x)2 · x3 · (-x)3; (6)(-y)2 · (-y)3 · (-y).
(4) y8 · (-y) = -y8+1 = -y9;
(5)(-x)2 · x3 · (-x)3 = -x2+3+3 = -x8;
(6)(-y)2 · (-y)3 · (-y) = y2+3+1 = y6.
课堂练习
3. 光的速度约为 3 × 105 km/s,太阳光照射到地球上
大约需要 5 × 102 s,地球距离太阳大约有多远?
解:3 ×105 × 5×102 = 15×107 = 1.5×108(km)
答:地球距离太阳大约 108 km.
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
am · an = am+n(m,n 都是正整数).
同底数幂相乘,底数不变,指数相加.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第八章 整式乘法与因式分解 8.1.1 幂的运算
同底数幂的乘法
沪科版(2024)七年级下册数学课件
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 什么叫乘方?
求几个相同因数的积的运算叫作乘方.
2. 25 表示什么?
2×2×2×2×2
3. 10×10×10×10×10 可以写成什么形式?
105
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. (-2)×(-2) ×(-2) = (-2)( )
2. a·a·a·a·a = a ( )
3. x4 = ( )
4. (-2)7 = -( )7 (-3)8 = ( )8
做 一 做
3
5
x · x · x · x
2
3
新课讲解
思考:an 表示的意义是什么?其中 a、n、an 分别叫作什么?
an
指数
幂
底数
= a·a····a
n 个 a
新课讲解
例题 中国设计并制造的“神威·太湖之光”是世界上首台峰值性能超过每秒 10 亿亿次的超级计算机. 峰值运算性能高达 1.25×1017 次/s,它工作 1 h(3.6×103 s)可进行多少次运算?
(1.25×1017)×(3.6×103)
=1.25×3.6×1017×103
=?
新课讲解
算 式 运算过程 结 果
22×23 (2×2)×(2×2×2) 25
103×104
a2 · a3
a4 · a5
am,an是两个同底数的幂,简称“同底数幂”,怎样计算 am· an?
先填写下列表格:
思 考
(10×10×10)×( 10×10×10×10 )
107
(a·a)·(a·a·a)
(a·a·a·a)·(a·a·a·a·a)
a9
a5
新课讲解
算 式 结 果
22×23 25
103×104
a2 · a3
a4 · a5
107
a9
a5
观察下表,同底数幂相乘有什么规律?
底数不变
指数相加
猜想: am · an=
(当m、n都是正整数)
新课讲解
am · an =
= a · a · … · a
(m+n)个
= am+n
一般地,如果 m,n 都是正整数,那么
( a · a · … · a )
( a · a · … · a )
m个
n个
·
新课讲解
由此得幂的运算性质 1:
am · an = am+n(m,n 都是正整数).
同底数幂相乘,底数不变,指数相加.
新课讲解
思考 当三个或三个以上同底数幂相乘时,是否也具有这一性质呢? 怎样用公式表示?
如 am · an · ap =
am+n+p
(m、n、p都是正整数)
新课讲解
计算:
例 1
(1) ;
(2)(-2)2×(-2)7;
(2)(-2)2×(-2)7 = (-2)2+7 = (-2)9 = -29.
新课讲解
计算:
(3)a2 · a3 · a6;
(4)(-y)3 · y4.
(3)a2 · a3 · a6 = a2+3+6 = a11.
(4)(-y)3 · y4 = (-y3)·y4 = -(y3·y4) = -y3+4 = -y7.
新课讲解
例 1
练 习
1. 下面的计算是否正确?为什么?
(1)x3 + x3 = x6.
(2)x3 · x3 = 2x3.
(3)c · c3 = c3.
(4)c + c3 = c4.
( )
( )
( )
( )
×
2x3
×
x6
×
c4
×
c(c2+1)
课堂练习
2. 计算:
(1)105 × 103; (2)-a2 · a5 ;
(3)-x3 · x5; (4) y8 · (-y);
(5)(-x)2 · x3 · (-x)3; (6)(-y)2 · (-y)3 · (-y).
解:(1)105 × 103 = 105+3 = 108;
(2)-a2 · a5 = -a2+5 = -a7;
(3)-x3 · x5 = -x3+5 = -x8;
课堂练习
2. 计算:
(1)105 × 103; (2)-a2 · a5 ;
(3)-x3 · x5; (4) y8 · (-y);
(5)(-x)2 · x3 · (-x)3; (6)(-y)2 · (-y)3 · (-y).
(4) y8 · (-y) = -y8+1 = -y9;
(5)(-x)2 · x3 · (-x)3 = -x2+3+3 = -x8;
(6)(-y)2 · (-y)3 · (-y) = y2+3+1 = y6.
课堂练习
3. 光的速度约为 3 × 105 km/s,太阳光照射到地球上
大约需要 5 × 102 s,地球距离太阳大约有多远?
解:3 ×105 × 5×102 = 15×107 = 1.5×108(km)
答:地球距离太阳大约 108 km.
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
am · an = am+n(m,n 都是正整数).
同底数幂相乘,底数不变,指数相加.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
