华师大版七下(2024版)第八单元三角形大单元教学设计
文档属性
| 名称 | 华师大版七下(2024版)第八单元三角形大单元教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 310.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-24 11:18:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
学 科 数学 年 级 七年级 设计者
教材版本 华师版 册、章 七年级下册第八章
课标要求 内容要求: (1)理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性。 (2)探索并证明三角形的内角和定理。掌握它的推论:三角形的外角等于与它不相邻的两个内角的和。 (3)证明三角形的任意两边之和大于第三边。
(4)理解等腰三角形、等边三角形及直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余。 (5)了解多边形的概念及多边形的顶点、边、内角、外角与对角线;探索并掌握多边形内角和与外角和公式。 (6)通过正多边形的拼接体会与思考数学知识在解决现实生活的问题中的价值,从中进 步思考与体验数学美的应用价值。
内容分析 华师大版初中数学七年级下册的《第八章三角形》是几何学习中的一个重要章节,它不仅承载着对三角形基础概念和性质的全面介绍,还扮演着连接学生先前所学与后续几何知识深入探索的桥梁角色。本章内容丰富多彩,深入浅出地引导学生走进三角形的奇妙世界,为他们构建一个系统而坚实的几何知识体系。在这一章节中,由现实生活的物体抽象出几何图形,由地面的瓷砖铺设引出最简单的多边形---三角形。 学生们将首先认识与三角形的基本概念和有关的边,包括边、高、中线以及角平分线,了解三角形的分类等;章节还深入探讨了三角形的角,包括内角和外角。学生将学习如何计算三角形的内角和,这一基础知识是证明许多三角形性质的基础。外角的概念及其与相邻内角的关系,也将被详尽阐述,帮助学生从多角度审视三角形的角特征,培养他们的空间想象力和逻辑推理能力。 接着深入探索了三角形的三边关系,在小学阶段通过观察或度量,了解到“三角形的任意两边之和大于第三边”这样一个事实的基础上,通过作三角形的过程,再次体会这一结论,会运用这个结论进行简单的计算和推理,进而深入理解三角形的稳定性及其在现实生活中的应用. 本章还拓展到了多边形的内角和与外角和的内容,进一步丰富了学生的几何视野。多边形作为三角形的延伸,其内角和的计算方法不仅加深了学生对几何图形内在规律的认识,也为后续学习更复杂几何图形打下了坚实的基础。 更为重要的是,本单元的教学不仅仅局限于理论知识的传授,更注重培养学生的实践操作能力和逻辑推理能力。通过用正多边形铺设地面活动,学生被鼓励亲自动手,体验知识的生成过程,从而在实践中深化对三角形性质的理解。这种“做中学”的方式,极大地提升了学生的学习兴趣和参与度,使他们在探索中发现几何之美,培养解决问题的能力和创新思维。
学情分析 经过前期系统学习,学生已构建起几何知识的基础框架,具体表现为: 在平面图形认知方面,学生已系统掌握直线、射线、线段的本质特征:直线具有双向无限延伸性,射线呈现单向无限延伸性,线段则是具有确定长度的有限图形。这些基础几何元素的认知,为后续三角形知识的学习奠定了重要基础。在角的概念体系构建上,学生已从直观的角度测量进阶到对角的性质研究,能够理解角平分线、邻补角、互补角等概念的内涵与外延。 几何操作技能方面,学生已具备使用直尺、圆规进行基础作图的能力,能够规范绘制直线、射线、线段及角等基本图形。这种操作能力不仅是几何学习的基础技能,更是培养空间想象能力和几何直观素养的重要载体。在实际操作过程中,学生需要将图形性质与操作步骤进行有机结合,这对其数学思维的严谨性提出了明确要求。 数学能力储备方面,学生已具备代数运算与逻辑推理的双重能力支撑。在代数领域,他们能够熟练进行有理数运算和代数式变形,这种运算能力为解决三角形相关的数值问题提供了有力工具。在逻辑推理方面,学生能够运用归纳、类比等合情推理方法发现几何规律,同时也初步掌握了从已知条件出发进行演绎推理的能力,这种思维能力为三角形性质的探究和证明奠定了重要基础。
单元目标 (一)教学目标 ①理解三角形的内角、边、主要线段及多边形的内角的概念;了解三角形的分类的方法;掌握三角形的三边关系的知识并会合理应用其解决问题;了解三角形的稳定性;探索并掌握三角形的内角和与外角性质,以及多边形的内角和与外角和,在有关的计算中能正确的使用解决问题。 ②经历从具体到抽象、从特殊到一般的认知过程培养观察归纳推理等能力;通过画图找规律度量推理证明等活动体验数学探究的乐趣和成就感;学会运用信息技术手段辅助儿何学习提高学习效率和兴趣。 ③感受多边形知识在日常生活中的应用价值,欣赏正多边形密铺的数学美感,感悟几何规律的普适性,体会三角形的稳定性在生活中的应用,思考其中的数学规律在三角形的内角和与外角和的知识形成的意义与作用。 (二)教学重点、难点 重点:三角形的有关概念及三角形的分类,三角形三边关系定理的应用与几何作图,三角形内角和定理与外角性质的推导及应用;多边形内角和与外角和公式的探究与计算;正多边形密铺的条件分析与图案设计。 难点:三角形三边关系的动态理解与实际问题转化;多边形内角和公式的推导过程;外角性质在复杂图形中的灵活运用;密铺问题的数学建模与跨学科应用。
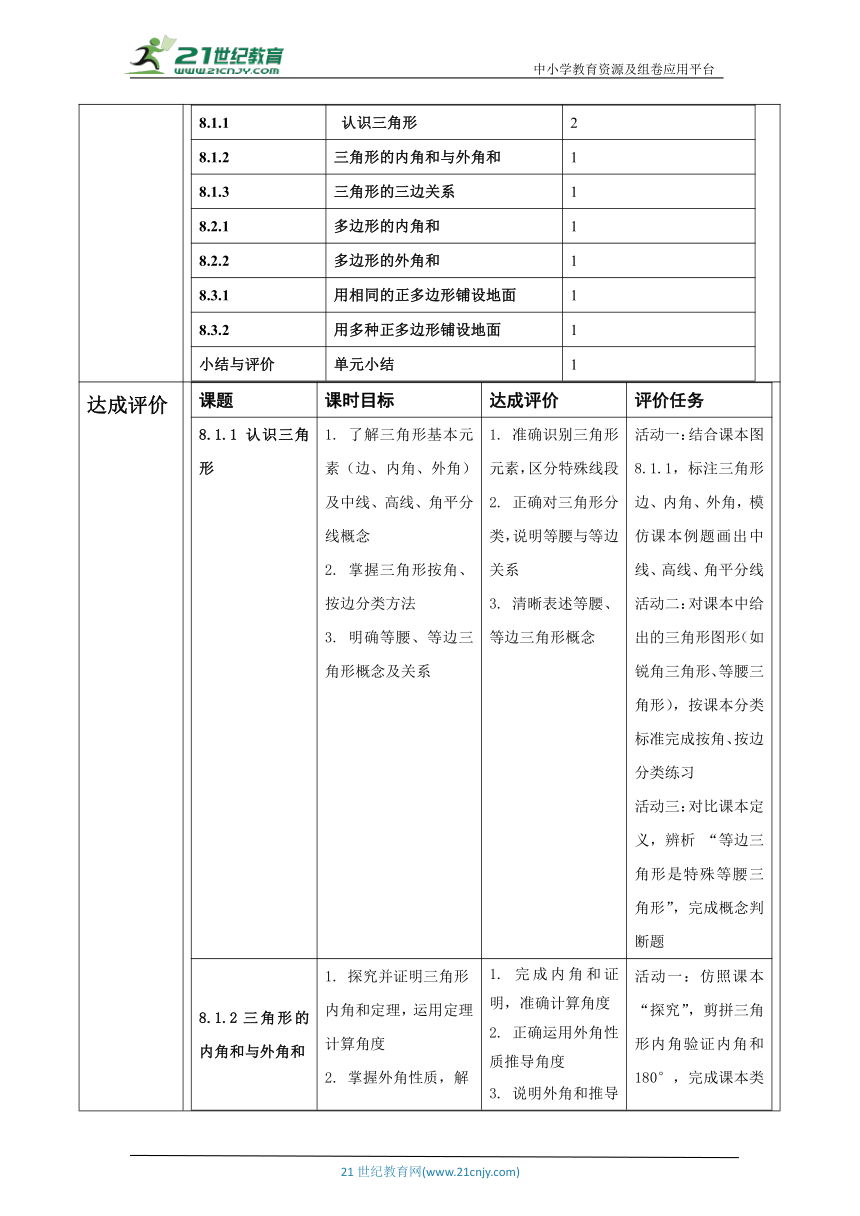
单元知识结构框架及课时安排 (一)单元知识结构框架 (二)课时安排 课时编号单元主要内容课时数8.1.1 认识三角形28.1.2三角形的内角和与外角和18.1.3 三角形的三边关系18.2.1多边形的内角和18.2.2多边形的外角和18.3.1用相同的正多边形铺设地面18.3.2用多种正多边形铺设地面 1小结与评价单元小结1
达成评价 课题课时目标达成评价评价任务8.1.1 认识三角形1. 了解三角形基本元素(边、内角、外角)及中线、高线、角平分线概念 2. 掌握三角形按角、按边分类方法 3. 明确等腰、等边三角形概念及关系1. 准确识别三角形元素,区分特殊线段 2. 正确对三角形分类,说明等腰与等边关系 3. 清晰表述等腰、等边三角形概念活动一:结合课本图 8.1.1,标注三角形边、内角、外角,模仿课本例题画出中线、高线、角平分线 活动二:对课本中给出的三角形图形(如锐角三角形、等腰三角形),按课本分类标准完成按角、按边分类练习 活动三:对比课本定义,辨析 “等边三角形是特殊等腰三角形”,完成概念判断题8.1.2三角形的内角和与外角和1. 探究并证明三角形内角和定理,运用定理计算角度 2. 掌握外角性质,解决角度推导问题 3. 理解三角形外角和为 360°1. 完成内角和证明,准确计算角度 2. 正确运用外角性质推导角度 3. 说明外角和推导过程活动一:仿照课本 “探究”,剪拼三角形内角验证内角和 180°,完成课本类似习题(已知两内角求第三角) 活动二:分析课本图 8.1.10,运用外角性质解决课本例题式角度推导(如已知外角和一不相邻内角,求另一内角) 活动三:小组合作,按课本思路推导三角形外角和,如分别计算三个外角并求和验证 360°8.1.3 三角形的三边关系1. 掌握三角形三边关系定理 2. 运用定理判断线段能否构成三角形 3. 解决已知两边求第三边范围问题1. 准确表述三边关系定理 2. 正确判断线段能否构成三角形 3. 求解第三边范围活动一:用课本 “做一做” 的线段长度(如 2cm、3cm、5cm)拼三角形,归纳三边关系 活动二:完成课本练习,判断给定线段(如 3、4、8)能否构成三角形 活动三:解决课本类似问题,如已知两边为 6 和 10,求第三边取值范围8.2.1多边形的内角和1. 推导多边形内角和公式 2. 运用公式计算内角和、边数等 3. 理解转化思想1. 阐述公式推导过程 2. 正确计算内角和、求边数 3. 体会转化思想活动一:参照课本,从四边形引对角线转化为三角形,推导五边形、六边形内角和,归纳 n 边形公式 活动二:完成课本习题,如求正七边形内角和,已知内角和为 1440° 求边数 活动三:分享课本中 “多边形转化为三角形” 的转化思想应用实例8.2.2多边形的外角和1. 掌握多边形外角和为 360° 2. 运用定理计算边数、外角度数 3. 区分内角和与外角和应用1. 说明外角和推导过程
2. 用定理求边数、外角度数
3. 正确选择定理解题活动一:仿照课本,从三角形、四边形外角和推导,得出多边形外角和定理
活动二:解决课本习题,如求正十二边形每个外角度数,已知每个外角为 60° 求边数
活动三:对比课本内角和与外角和例题,选择合适定理解答综合题8.3.1用相同的正多边形铺设地面1. 理解正多边形密铺条件 2. 判断正多边形能否单独密铺 3. 掌握正三角形等密铺原理1. 说明密铺条件 2. 准确判断密铺情况 3. 解释密铺原理活动一:按课本 “做一做”,用正三角形、正方形纸片尝试密铺,分析内角是否为 360° 约数
活动二:判断课本提及的正多边形(如正五边形、正六边形)能否单独密铺,结合课本内容说明理由
活动三:解释课本中 “正六边形能密铺” 的角度原理8.3.2用多种正多边形铺设地面 1. 探究组合密铺条件 2. 找出组合密铺方案 3. 理解角度匹配原理1. 说明组合密铺条件
2. 列举组合方案
3. 解释角度匹配活动一:分析课本图 8.3.3,计算正三角形与正方形组合的角度和(60°×3 + 90°×2 = 360°) 活动二:尝试课本式组合(如正三角形与正六边形),记录密铺方案 活动三:小组合作设计课本风格的多种正多边形密铺方案,说明角度匹配过程单元小结与评价1. 梳理知识体系
2. 综合运用知识解题
3. 反思数学思想1、通过对本单元知识点的小结与回顾,让学生形成知识体系. 2、通过解决本章重点例题,让学生学会用学过的知识解决实际问题,提升应用意识.活动一:参照课本章节结构,绘制包含三角形概念、性质,多边形公式等内容的思维导图
活动二:完成课本复习题,如综合三角形三边关系、内角和,多边形外角和的题目
活动三:结合课本例题,分享转化思想、分类讨论在本章的应用案例
21世纪教育网(www.21cnjy.com)
学 科 数学 年 级 七年级 设计者
教材版本 华师版 册、章 七年级下册第八章
课标要求 内容要求: (1)理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性。 (2)探索并证明三角形的内角和定理。掌握它的推论:三角形的外角等于与它不相邻的两个内角的和。 (3)证明三角形的任意两边之和大于第三边。
(4)理解等腰三角形、等边三角形及直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余。 (5)了解多边形的概念及多边形的顶点、边、内角、外角与对角线;探索并掌握多边形内角和与外角和公式。 (6)通过正多边形的拼接体会与思考数学知识在解决现实生活的问题中的价值,从中进 步思考与体验数学美的应用价值。
内容分析 华师大版初中数学七年级下册的《第八章三角形》是几何学习中的一个重要章节,它不仅承载着对三角形基础概念和性质的全面介绍,还扮演着连接学生先前所学与后续几何知识深入探索的桥梁角色。本章内容丰富多彩,深入浅出地引导学生走进三角形的奇妙世界,为他们构建一个系统而坚实的几何知识体系。在这一章节中,由现实生活的物体抽象出几何图形,由地面的瓷砖铺设引出最简单的多边形---三角形。 学生们将首先认识与三角形的基本概念和有关的边,包括边、高、中线以及角平分线,了解三角形的分类等;章节还深入探讨了三角形的角,包括内角和外角。学生将学习如何计算三角形的内角和,这一基础知识是证明许多三角形性质的基础。外角的概念及其与相邻内角的关系,也将被详尽阐述,帮助学生从多角度审视三角形的角特征,培养他们的空间想象力和逻辑推理能力。 接着深入探索了三角形的三边关系,在小学阶段通过观察或度量,了解到“三角形的任意两边之和大于第三边”这样一个事实的基础上,通过作三角形的过程,再次体会这一结论,会运用这个结论进行简单的计算和推理,进而深入理解三角形的稳定性及其在现实生活中的应用. 本章还拓展到了多边形的内角和与外角和的内容,进一步丰富了学生的几何视野。多边形作为三角形的延伸,其内角和的计算方法不仅加深了学生对几何图形内在规律的认识,也为后续学习更复杂几何图形打下了坚实的基础。 更为重要的是,本单元的教学不仅仅局限于理论知识的传授,更注重培养学生的实践操作能力和逻辑推理能力。通过用正多边形铺设地面活动,学生被鼓励亲自动手,体验知识的生成过程,从而在实践中深化对三角形性质的理解。这种“做中学”的方式,极大地提升了学生的学习兴趣和参与度,使他们在探索中发现几何之美,培养解决问题的能力和创新思维。
学情分析 经过前期系统学习,学生已构建起几何知识的基础框架,具体表现为: 在平面图形认知方面,学生已系统掌握直线、射线、线段的本质特征:直线具有双向无限延伸性,射线呈现单向无限延伸性,线段则是具有确定长度的有限图形。这些基础几何元素的认知,为后续三角形知识的学习奠定了重要基础。在角的概念体系构建上,学生已从直观的角度测量进阶到对角的性质研究,能够理解角平分线、邻补角、互补角等概念的内涵与外延。 几何操作技能方面,学生已具备使用直尺、圆规进行基础作图的能力,能够规范绘制直线、射线、线段及角等基本图形。这种操作能力不仅是几何学习的基础技能,更是培养空间想象能力和几何直观素养的重要载体。在实际操作过程中,学生需要将图形性质与操作步骤进行有机结合,这对其数学思维的严谨性提出了明确要求。 数学能力储备方面,学生已具备代数运算与逻辑推理的双重能力支撑。在代数领域,他们能够熟练进行有理数运算和代数式变形,这种运算能力为解决三角形相关的数值问题提供了有力工具。在逻辑推理方面,学生能够运用归纳、类比等合情推理方法发现几何规律,同时也初步掌握了从已知条件出发进行演绎推理的能力,这种思维能力为三角形性质的探究和证明奠定了重要基础。
单元目标 (一)教学目标 ①理解三角形的内角、边、主要线段及多边形的内角的概念;了解三角形的分类的方法;掌握三角形的三边关系的知识并会合理应用其解决问题;了解三角形的稳定性;探索并掌握三角形的内角和与外角性质,以及多边形的内角和与外角和,在有关的计算中能正确的使用解决问题。 ②经历从具体到抽象、从特殊到一般的认知过程培养观察归纳推理等能力;通过画图找规律度量推理证明等活动体验数学探究的乐趣和成就感;学会运用信息技术手段辅助儿何学习提高学习效率和兴趣。 ③感受多边形知识在日常生活中的应用价值,欣赏正多边形密铺的数学美感,感悟几何规律的普适性,体会三角形的稳定性在生活中的应用,思考其中的数学规律在三角形的内角和与外角和的知识形成的意义与作用。 (二)教学重点、难点 重点:三角形的有关概念及三角形的分类,三角形三边关系定理的应用与几何作图,三角形内角和定理与外角性质的推导及应用;多边形内角和与外角和公式的探究与计算;正多边形密铺的条件分析与图案设计。 难点:三角形三边关系的动态理解与实际问题转化;多边形内角和公式的推导过程;外角性质在复杂图形中的灵活运用;密铺问题的数学建模与跨学科应用。
单元知识结构框架及课时安排 (一)单元知识结构框架 (二)课时安排 课时编号单元主要内容课时数8.1.1 认识三角形28.1.2三角形的内角和与外角和18.1.3 三角形的三边关系18.2.1多边形的内角和18.2.2多边形的外角和18.3.1用相同的正多边形铺设地面18.3.2用多种正多边形铺设地面 1小结与评价单元小结1
达成评价 课题课时目标达成评价评价任务8.1.1 认识三角形1. 了解三角形基本元素(边、内角、外角)及中线、高线、角平分线概念 2. 掌握三角形按角、按边分类方法 3. 明确等腰、等边三角形概念及关系1. 准确识别三角形元素,区分特殊线段 2. 正确对三角形分类,说明等腰与等边关系 3. 清晰表述等腰、等边三角形概念活动一:结合课本图 8.1.1,标注三角形边、内角、外角,模仿课本例题画出中线、高线、角平分线 活动二:对课本中给出的三角形图形(如锐角三角形、等腰三角形),按课本分类标准完成按角、按边分类练习 活动三:对比课本定义,辨析 “等边三角形是特殊等腰三角形”,完成概念判断题8.1.2三角形的内角和与外角和1. 探究并证明三角形内角和定理,运用定理计算角度 2. 掌握外角性质,解决角度推导问题 3. 理解三角形外角和为 360°1. 完成内角和证明,准确计算角度 2. 正确运用外角性质推导角度 3. 说明外角和推导过程活动一:仿照课本 “探究”,剪拼三角形内角验证内角和 180°,完成课本类似习题(已知两内角求第三角) 活动二:分析课本图 8.1.10,运用外角性质解决课本例题式角度推导(如已知外角和一不相邻内角,求另一内角) 活动三:小组合作,按课本思路推导三角形外角和,如分别计算三个外角并求和验证 360°8.1.3 三角形的三边关系1. 掌握三角形三边关系定理 2. 运用定理判断线段能否构成三角形 3. 解决已知两边求第三边范围问题1. 准确表述三边关系定理 2. 正确判断线段能否构成三角形 3. 求解第三边范围活动一:用课本 “做一做” 的线段长度(如 2cm、3cm、5cm)拼三角形,归纳三边关系 活动二:完成课本练习,判断给定线段(如 3、4、8)能否构成三角形 活动三:解决课本类似问题,如已知两边为 6 和 10,求第三边取值范围8.2.1多边形的内角和1. 推导多边形内角和公式 2. 运用公式计算内角和、边数等 3. 理解转化思想1. 阐述公式推导过程 2. 正确计算内角和、求边数 3. 体会转化思想活动一:参照课本,从四边形引对角线转化为三角形,推导五边形、六边形内角和,归纳 n 边形公式 活动二:完成课本习题,如求正七边形内角和,已知内角和为 1440° 求边数 活动三:分享课本中 “多边形转化为三角形” 的转化思想应用实例8.2.2多边形的外角和1. 掌握多边形外角和为 360° 2. 运用定理计算边数、外角度数 3. 区分内角和与外角和应用1. 说明外角和推导过程
2. 用定理求边数、外角度数
3. 正确选择定理解题活动一:仿照课本,从三角形、四边形外角和推导,得出多边形外角和定理
活动二:解决课本习题,如求正十二边形每个外角度数,已知每个外角为 60° 求边数
活动三:对比课本内角和与外角和例题,选择合适定理解答综合题8.3.1用相同的正多边形铺设地面1. 理解正多边形密铺条件 2. 判断正多边形能否单独密铺 3. 掌握正三角形等密铺原理1. 说明密铺条件 2. 准确判断密铺情况 3. 解释密铺原理活动一:按课本 “做一做”,用正三角形、正方形纸片尝试密铺,分析内角是否为 360° 约数
活动二:判断课本提及的正多边形(如正五边形、正六边形)能否单独密铺,结合课本内容说明理由
活动三:解释课本中 “正六边形能密铺” 的角度原理8.3.2用多种正多边形铺设地面 1. 探究组合密铺条件 2. 找出组合密铺方案 3. 理解角度匹配原理1. 说明组合密铺条件
2. 列举组合方案
3. 解释角度匹配活动一:分析课本图 8.3.3,计算正三角形与正方形组合的角度和(60°×3 + 90°×2 = 360°) 活动二:尝试课本式组合(如正三角形与正六边形),记录密铺方案 活动三:小组合作设计课本风格的多种正多边形密铺方案,说明角度匹配过程单元小结与评价1. 梳理知识体系
2. 综合运用知识解题
3. 反思数学思想1、通过对本单元知识点的小结与回顾,让学生形成知识体系. 2、通过解决本章重点例题,让学生学会用学过的知识解决实际问题,提升应用意识.活动一:参照课本章节结构,绘制包含三角形概念、性质,多边形公式等内容的思维导图
活动二:完成课本复习题,如综合三角形三边关系、内角和,多边形外角和的题目
活动三:结合课本例题,分享转化思想、分类讨论在本章的应用案例
21世纪教育网(www.21cnjy.com)
