华师大版七下(2024版)8.1.1认识三角形第2课时 学案
文档属性
| 名称 | 华师大版七下(2024版)8.1.1认识三角形第2课时 学案 |  | |
| 格式 | docx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:56:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第8章三角形
8.1.1 认识三角形第2课时
学习目标与重难点
学习目标:
1.掌握三角形的中线、角平分线和高的定义,并能够对其进行简单的应用.
2. 能够准确的画出三角形的高、中线和角平分线.
学习重点:理解三角形的中线、角平分线、高的概念,会用工具准确画出三角形的高、中线、角平分线.
学习难点:掌握钝角三角形高的画法.
预习自测
一、知识链接
1.过直线外一点,画已知直线的垂线,能画几条?怎么画?
已知△ABC中,BC5 cm,高AD4 cm,求△ABC的面积.
自学自测
1.下列四个图形中,线段BE是△ABC的高的图形是( )
A. B.
C. D.
2.用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( )
A. B.
C. D.
3.下列说法错误的是( )
A.三角形的高、中线、角平分线都是线段
B.三角形的三条中线都在三角形内部
C.锐角三角形的三条高一定交于同一点
D.三角形的三条高、三条中线、三条角平分线都交于同一点
教学过程
一、创设情境、导入新课
思考:这里有一块三角形的蛋糕,如果兄弟两个想要平分的话,你该怎么办呢?本节我们一起来解决这个问题.
二、合作交流、新知探究
探究一:新知探究
教材第83页:
1、三角形的中线
三角形的一个顶点与它的对边中点的连线叫三角形的中线.如图,点D是BC边的中点,即AD是△ABC的中线.
思考:三角形有几条中线?若已知AD是三角形的中线,你可得到什么结论?
动手操作:分别画出锐角三角形、直角三角形、钝角三角形的三条中线,你发现什么规律?
【强调】:三角形的三条中线交于三角形内部一点,三角形的中线平分面积。
2、三角形的角平分线
教材第83页:
三角形内角的平分线与对边的交点和这个内角顶点之间的线段叫三角形的角平分线.
如图,∠1=∠2,那么CE是△ABC的角平分线.
思考:三角形有几条角平分线 三角形的角平分线和角的平分线有什么不同
动手操作:请画出这个三角形的另外两条角平分线,你发现了什么?
小组探究总结规律:
【强调】: 三角形的角平分线是线段
3、三角形的高
教材第83页:
过三角形顶点作对边的垂线,垂足与顶点间的线段叫三角形的高.
如图,BF⊥AC,垂足为F,则BF是△ABC的高,三角形有3条高.
动手操作:分别画出锐角三角形、直角三角形、钝角三角形的三条高,你发现什么规律?
强调:钝角三角形除最长边上的高外,其余两边上的高在三角形外部,垂足在该边的延长线上。
探究三:例题讲解
例1. 在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
例2. 如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=________.
例3.如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为________.
例4. 如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( ).
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
A. 4个 B.3个 C.2个 D.1个
三、课堂练习、巩固提高
必做题:
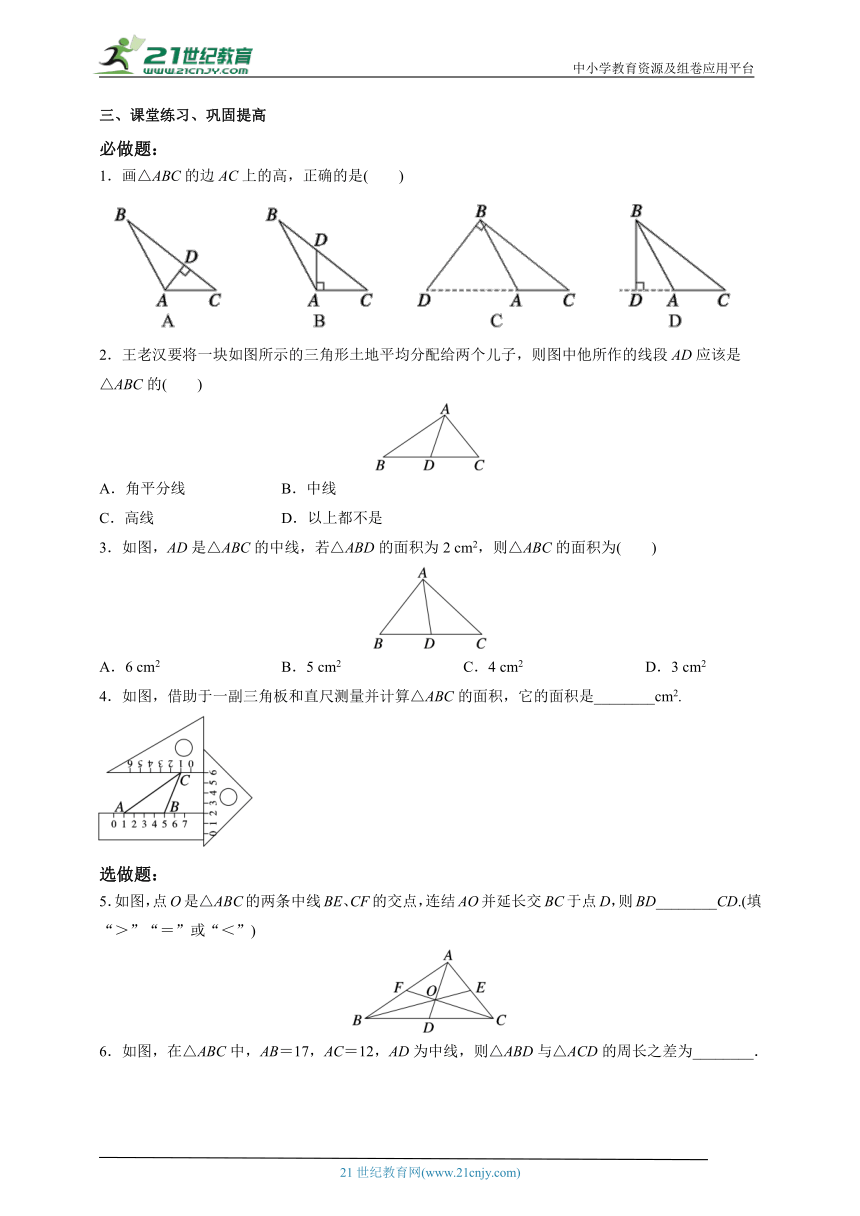
1.画△ABC的边AC上的高,正确的是( )
2.王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
A.角平分线 B.中线
C.高线 D.以上都不是
3.如图,AD是△ABC的中线,若△ABD的面积为2 cm2,则△ABC的面积为( )
A.6 cm2 B.5 cm2 C.4 cm2 D.3 cm2
4.如图,借助于一副三角板和直尺测量并计算△ABC的面积,它的面积是________cm2.
选做题:
5.如图,点O是△ABC的两条中线BE、CF的交点,连结AO并延长交BC于点D,则BD________CD.(填“>”“=”或“<”)
6.如图,在△ABC中,AB=17,AC=12,AD为中线,则△ABD与△ACD的周长之差为________.
【综合拓展类作业】
7.如图,已知三角形的内角和等于180°,直角三角形ABC中,∠ACB=90°,点P为AC上一点,连结BP,∠ABP=∠ABC.
(1)BP是△ABC的________;(填“高”“中线”或“角平分线”)
(2)若∠A=34°,求∠BPC的度数.
总结反思、拓展升华
【课堂总结】
知识点:
1.三角形的高:从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高.
2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.
3.三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点与交点的线段叫做三角形的角平分线.
数学思想: 数形结合思想
注意事项:1、三角形的三条中线交于三角形内部一点,三角形的中线平分面积。
2、三角形的角平分线是一条线段。
3、钝角三角形的两条高在外部。
五、【作业布置】
必做题:
1.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠ADC=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
2.如图所示,BA⊥AC,AD⊥BC,垂足分别为A、D,已知AB=6,AC=8,BC=10,AD=4.8,则点A到线段BC的距离是( )
A.10 B.8 C.6 D.4.8
3.如图,△ABC的面积是10,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
A. B. C. D.
选做题:
4.如图,已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为16,则△ABE的面积为________.
5.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,AB=12 cm,BC=13 cm,AC=5 cm.求:
(1)△ABC的面积;
(2)AD的长.
【综合拓展类作业】
6.如图,在△ABC中,AD是△ABC的角平分线,DE∥AB,DF∥AC,EF交AD于点O.
(1)试说明:DO是△EDF的角平分线;
(2)若将(1)中结论与AD是△ABC的角平分线,DE∥AB,DF∥AC中的任何一个条件交换,所得说法正确吗?请选择一个说明.
答案:
自学测试:
1.A;2.B;3D.
课堂巩固:
答案:1.D 2.B 3.C
4.8 5.= 6.5
7.解:(1)角平分线
(2)∵∠ACB=90°,∠A=34°,
∴∠ABC=180°-90°-34°=56°.
∴∠ABP=∠CBP=28°.
∴∠BPC=180°-90°-28°=62°.
作业布置:
答案:1.C 解析:∵AF是△ABC的中线,
∴BF=CF.A说法正确,不符合题意;
∵AD是高,∴∠ADC=90°.
B说法正确,不符合题意;
∵AE是角平分线,
∴∠BAE=∠CAE.∴∠BAF与
∠CAF不相等,C说法错误,符合题意;
∵BF=CF,
∴S△ABC=2S△ABF.D说法正确,不符合题意.故选C.
2.D 解析:∵AD⊥BC,AD=4.8,
∴点A到线段BC的距离是4.8.故选D.
3.D 解析:连结BG,如图所示.
∵点D是BC的中点,S△ABC=10,
∴S△ABD=S△ACD=S△ABC=5.
∵点E是AD的中点,
∴S△ABE=S△DBE=S△ABD=,S△ACE=S△DCE=S△ACD=.
∴S△ABE+S△ACE=+=5.
∴S△BEC=S△ABC-(S△ABE+S△ACE)=10-5=5.
∵点F是BE的中点,点G是CE的中点,
∴S△AEF=S△ABF=S△ABE=,S△AEG=S△ACG=S△ACE=.
∵点G是CE的中点,
∴S△BEG=S△BCG=S△BEC=.
∵点F是BE的中点,
∴S△EFG=S△BGF=S△BEG=.
∴S△AEF=S△AEG=S△EFG=.
∴S△AFG=S△AEF+S△AEG+S△EFG=3×=.故选D.
4.4 解析:∵AD是△ABC的中线,△ABC的面积为16,
∴△ABD的面积=△ABC的面积=×16=8.
∵BE是△ABD的中线,
∴△ABE的面积=△ABD的面积=×8=4.
5.解:(1)∵在△ABC中,∠BAC=90°,AC=5 cm,AB=12 cm,
∴S△ABC=AC·AB=×5×12=30(cm2).
(2)∵AD是BC边上的高,
∴S△ABC=BC·AD=30 cm2.
设AD=x cm,则×13×x=30,解得x=,∴AD= cm.
6.解:(1)如图,∵AD是△ABC的角平分线,
∴∠1=∠2.
∵DE∥AB,∴∠3=∠2.
∵DF∥AC,∴∠1=∠4.
∴∠3=∠4,即DO是∠EDF的平分线.
∴DO是△EDF的角平分线.
(2)所得说法正确.如:“DO是△EDF
的角平分线”与“DF∥AC”交换(答案不唯一).理由如下:
如图,∵AD是△ABC的角平分线,∴∠1=∠2.
∵DE∥AB,∴∠3=∠2.
∵DO是△EDF的角平分线,∴∠3=∠4.
∴∠1=∠4.∴DF∥AC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第8章三角形
8.1.1 认识三角形第2课时
学习目标与重难点
学习目标:
1.掌握三角形的中线、角平分线和高的定义,并能够对其进行简单的应用.
2. 能够准确的画出三角形的高、中线和角平分线.
学习重点:理解三角形的中线、角平分线、高的概念,会用工具准确画出三角形的高、中线、角平分线.
学习难点:掌握钝角三角形高的画法.
预习自测
一、知识链接
1.过直线外一点,画已知直线的垂线,能画几条?怎么画?
已知△ABC中,BC5 cm,高AD4 cm,求△ABC的面积.
自学自测
1.下列四个图形中,线段BE是△ABC的高的图形是( )
A. B.
C. D.
2.用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是( )
A. B.
C. D.
3.下列说法错误的是( )
A.三角形的高、中线、角平分线都是线段
B.三角形的三条中线都在三角形内部
C.锐角三角形的三条高一定交于同一点
D.三角形的三条高、三条中线、三条角平分线都交于同一点
教学过程
一、创设情境、导入新课
思考:这里有一块三角形的蛋糕,如果兄弟两个想要平分的话,你该怎么办呢?本节我们一起来解决这个问题.
二、合作交流、新知探究
探究一:新知探究
教材第83页:
1、三角形的中线
三角形的一个顶点与它的对边中点的连线叫三角形的中线.如图,点D是BC边的中点,即AD是△ABC的中线.
思考:三角形有几条中线?若已知AD是三角形的中线,你可得到什么结论?
动手操作:分别画出锐角三角形、直角三角形、钝角三角形的三条中线,你发现什么规律?
【强调】:三角形的三条中线交于三角形内部一点,三角形的中线平分面积。
2、三角形的角平分线
教材第83页:
三角形内角的平分线与对边的交点和这个内角顶点之间的线段叫三角形的角平分线.
如图,∠1=∠2,那么CE是△ABC的角平分线.
思考:三角形有几条角平分线 三角形的角平分线和角的平分线有什么不同
动手操作:请画出这个三角形的另外两条角平分线,你发现了什么?
小组探究总结规律:
【强调】: 三角形的角平分线是线段
3、三角形的高
教材第83页:
过三角形顶点作对边的垂线,垂足与顶点间的线段叫三角形的高.
如图,BF⊥AC,垂足为F,则BF是△ABC的高,三角形有3条高.
动手操作:分别画出锐角三角形、直角三角形、钝角三角形的三条高,你发现什么规律?
强调:钝角三角形除最长边上的高外,其余两边上的高在三角形外部,垂足在该边的延长线上。
探究三:例题讲解
例1. 在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
例2. 如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=________.
例3.如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为________.
例4. 如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( ).
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
A. 4个 B.3个 C.2个 D.1个
三、课堂练习、巩固提高
必做题:
1.画△ABC的边AC上的高,正确的是( )
2.王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
A.角平分线 B.中线
C.高线 D.以上都不是
3.如图,AD是△ABC的中线,若△ABD的面积为2 cm2,则△ABC的面积为( )
A.6 cm2 B.5 cm2 C.4 cm2 D.3 cm2
4.如图,借助于一副三角板和直尺测量并计算△ABC的面积,它的面积是________cm2.
选做题:
5.如图,点O是△ABC的两条中线BE、CF的交点,连结AO并延长交BC于点D,则BD________CD.(填“>”“=”或“<”)
6.如图,在△ABC中,AB=17,AC=12,AD为中线,则△ABD与△ACD的周长之差为________.
【综合拓展类作业】
7.如图,已知三角形的内角和等于180°,直角三角形ABC中,∠ACB=90°,点P为AC上一点,连结BP,∠ABP=∠ABC.
(1)BP是△ABC的________;(填“高”“中线”或“角平分线”)
(2)若∠A=34°,求∠BPC的度数.
总结反思、拓展升华
【课堂总结】
知识点:
1.三角形的高:从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高.
2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.
3.三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点与交点的线段叫做三角形的角平分线.
数学思想: 数形结合思想
注意事项:1、三角形的三条中线交于三角形内部一点,三角形的中线平分面积。
2、三角形的角平分线是一条线段。
3、钝角三角形的两条高在外部。
五、【作业布置】
必做题:
1.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠ADC=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
2.如图所示,BA⊥AC,AD⊥BC,垂足分别为A、D,已知AB=6,AC=8,BC=10,AD=4.8,则点A到线段BC的距离是( )
A.10 B.8 C.6 D.4.8
3.如图,△ABC的面积是10,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
A. B. C. D.
选做题:
4.如图,已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为16,则△ABE的面积为________.
5.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,AB=12 cm,BC=13 cm,AC=5 cm.求:
(1)△ABC的面积;
(2)AD的长.
【综合拓展类作业】
6.如图,在△ABC中,AD是△ABC的角平分线,DE∥AB,DF∥AC,EF交AD于点O.
(1)试说明:DO是△EDF的角平分线;
(2)若将(1)中结论与AD是△ABC的角平分线,DE∥AB,DF∥AC中的任何一个条件交换,所得说法正确吗?请选择一个说明.
答案:
自学测试:
1.A;2.B;3D.
课堂巩固:
答案:1.D 2.B 3.C
4.8 5.= 6.5
7.解:(1)角平分线
(2)∵∠ACB=90°,∠A=34°,
∴∠ABC=180°-90°-34°=56°.
∴∠ABP=∠CBP=28°.
∴∠BPC=180°-90°-28°=62°.
作业布置:
答案:1.C 解析:∵AF是△ABC的中线,
∴BF=CF.A说法正确,不符合题意;
∵AD是高,∴∠ADC=90°.
B说法正确,不符合题意;
∵AE是角平分线,
∴∠BAE=∠CAE.∴∠BAF与
∠CAF不相等,C说法错误,符合题意;
∵BF=CF,
∴S△ABC=2S△ABF.D说法正确,不符合题意.故选C.
2.D 解析:∵AD⊥BC,AD=4.8,
∴点A到线段BC的距离是4.8.故选D.
3.D 解析:连结BG,如图所示.
∵点D是BC的中点,S△ABC=10,
∴S△ABD=S△ACD=S△ABC=5.
∵点E是AD的中点,
∴S△ABE=S△DBE=S△ABD=,S△ACE=S△DCE=S△ACD=.
∴S△ABE+S△ACE=+=5.
∴S△BEC=S△ABC-(S△ABE+S△ACE)=10-5=5.
∵点F是BE的中点,点G是CE的中点,
∴S△AEF=S△ABF=S△ABE=,S△AEG=S△ACG=S△ACE=.
∵点G是CE的中点,
∴S△BEG=S△BCG=S△BEC=.
∵点F是BE的中点,
∴S△EFG=S△BGF=S△BEG=.
∴S△AEF=S△AEG=S△EFG=.
∴S△AFG=S△AEF+S△AEG+S△EFG=3×=.故选D.
4.4 解析:∵AD是△ABC的中线,△ABC的面积为16,
∴△ABD的面积=△ABC的面积=×16=8.
∵BE是△ABD的中线,
∴△ABE的面积=△ABD的面积=×8=4.
5.解:(1)∵在△ABC中,∠BAC=90°,AC=5 cm,AB=12 cm,
∴S△ABC=AC·AB=×5×12=30(cm2).
(2)∵AD是BC边上的高,
∴S△ABC=BC·AD=30 cm2.
设AD=x cm,则×13×x=30,解得x=,∴AD= cm.
6.解:(1)如图,∵AD是△ABC的角平分线,
∴∠1=∠2.
∵DE∥AB,∴∠3=∠2.
∵DF∥AC,∴∠1=∠4.
∴∠3=∠4,即DO是∠EDF的平分线.
∴DO是△EDF的角平分线.
(2)所得说法正确.如:“DO是△EDF
的角平分线”与“DF∥AC”交换(答案不唯一).理由如下:
如图,∵AD是△ABC的角平分线,∴∠1=∠2.
∵DE∥AB,∴∠3=∠2.
∵DO是△EDF的角平分线,∴∠3=∠4.
∴∠1=∠4.∴DF∥AC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
