期中重难点检测卷-2024-2025学年数学五年级下册苏教版(含解析)
文档属性
| 名称 | 期中重难点检测卷-2024-2025学年数学五年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 734.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 12:19:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期中重难点检测卷-2024-2025学年数学五年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面情况中,( )比较适合用折线统计图表示。
A.学校一年级~六年级男女生人数 B.第3小组记录蒜叶生长的变化情况
C.五年级各班参加数学兴趣小组的人数 D.五年级6个班制作的科技作品个数
2.如图中前两架天平保持平衡。根据图中的等量关系,你觉得第三架天平的右边放( )个才能使天平保持平衡。
A.6 B.5 C.4 D.3
3.一个三位数,既是2的倍数又是5的倍数,这个数最大是( )。
A.998 B.995 C.990 D.999
4.王阿姨家在三块菜地里种了1000棵番茄,第一块菜地里种的番茄比第二块少50棵,第三块菜地里种的番茄比第二块多150棵。第二块菜地里种番茄( )棵。
A.450 B.350 C.300 D.250
5. A=2×3×5,B=2×3×7,那么A和B的最大公因数是( ),最小公倍数是( )。
A.10;420 B.6;210 C.210;10 D.420;6
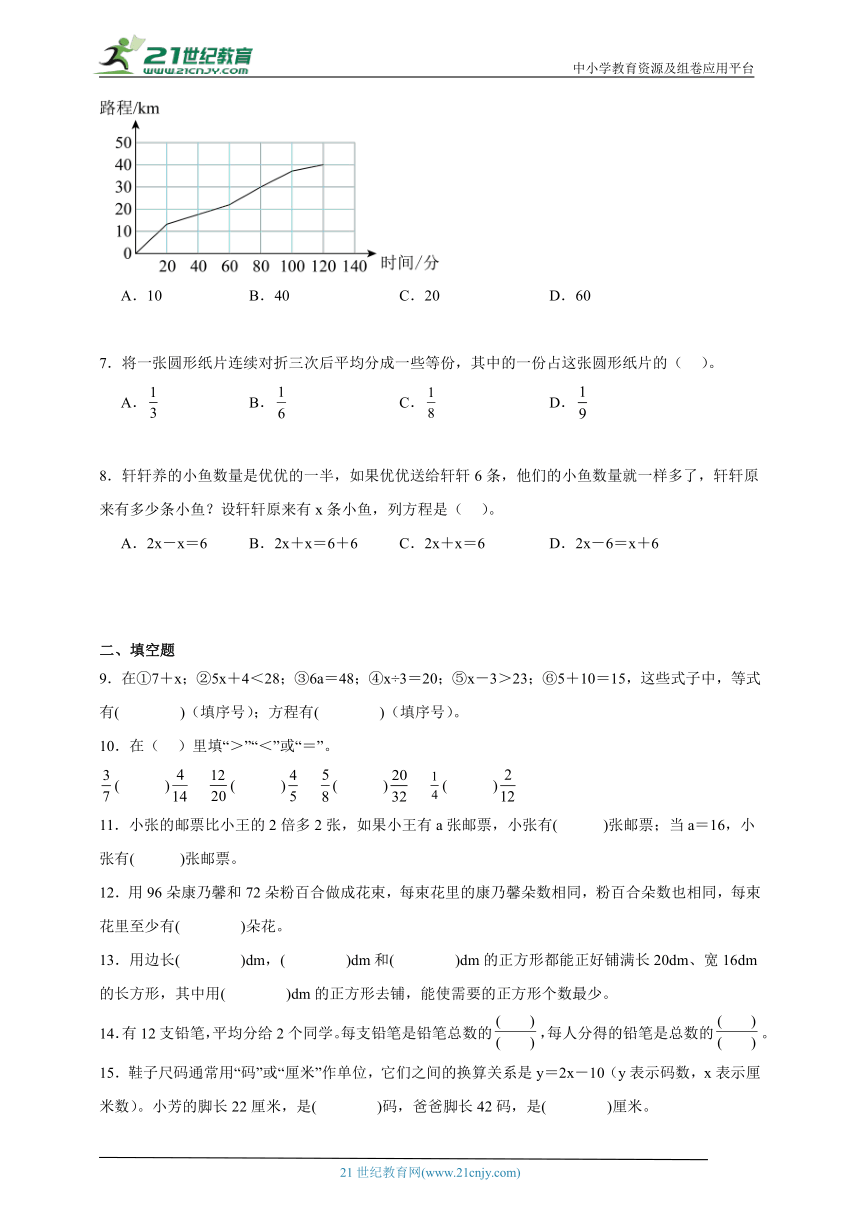
6.李叔叔参加一项全程40千米的山地自行车赛,如图显示了不同时间他骑行的路程。他骑行最后10千米用了( )分钟。
A.10 B.40 C.20 D.60
7.将一张圆形纸片连续对折三次后平均分成一些等份,其中的一份占这张圆形纸片的( )。
A. B. C. D.
8.轩轩养的小鱼数量是优优的一半,如果优优送给轩轩6条,他们的小鱼数量就一样多了,轩轩原来有多少条小鱼?设轩轩原来有x条小鱼,列方程是( )。
A.2x-x=6 B.2x+x=6+6 C.2x+x=6 D.2x-6=x+6
二、填空题
9.在①7+x;②5x+4<28;③6a=48;④x÷3=20;⑤x-3>23;⑥5+10=15,这些式子中,等式有( )(填序号);方程有( )(填序号)。
10.在( )里填“>”“<”或“=”。
( ) ( ) ( ) ( )
11.小张的邮票比小王的2倍多2张,如果小王有a张邮票,小张有( )张邮票;当a=16,小张有( )张邮票。
12.用96朵康乃馨和72朵粉百合做成花束,每束花里的康乃馨朵数相同,粉百合朵数也相同,每束花里至少有( )朵花。
13.用边长( )dm,( )dm和( )dm的正方形都能正好铺满长20dm、宽16dm的长方形,其中用( )dm的正方形去铺,能使需要的正方形个数最少。
14.有12支铅笔,平均分给2个同学。每支铅笔是铅笔总数的,每人分得的铅笔是总数的。
15.鞋子尺码通常用“码”或“厘米”作单位,它们之间的换算关系是y=2x-10(y表示码数,x表示厘米数)。小芳的脚长22厘米,是( )码,爸爸脚长42码,是( )厘米。
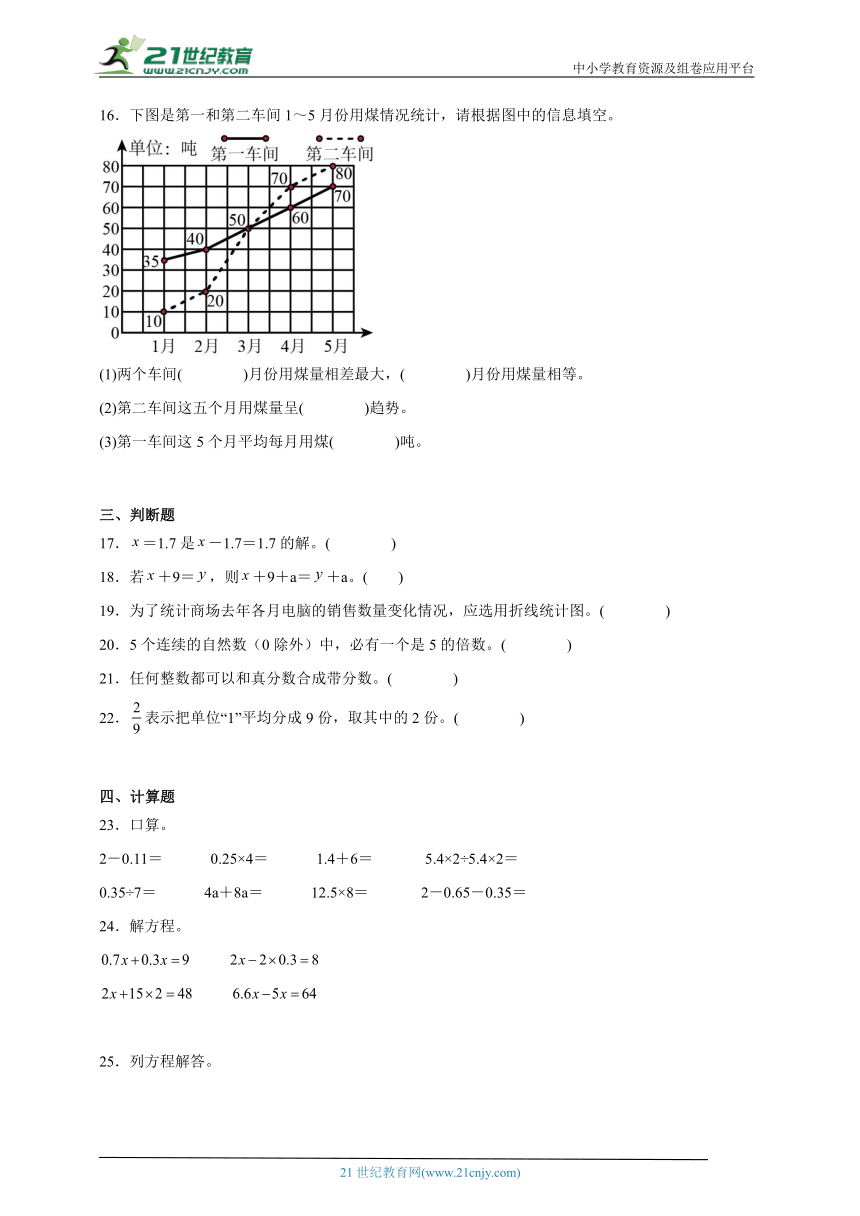
16.下图是第一和第二车间1~5月份用煤情况统计,请根据图中的信息填空。
(1)两个车间( )月份用煤量相差最大,( )月份用煤量相等。
(2)第二车间这五个月用煤量呈( )趋势。
(3)第一车间这5个月平均每月用煤( )吨。
三、判断题
17.=1.7是-1.7=1.7的解。( )
18.若+9=,则+9+a=+a。( )
19.为了统计商场去年各月电脑的销售数量变化情况,应选用折线统计图。( )
20.5个连续的自然数(0除外)中,必有一个是5的倍数。( )
21.任何整数都可以和真分数合成带分数。( )
22.表示把单位“1”平均分成9份,取其中的2份。( )
四、计算题
23.口算。
2-0.11= 0.25×4= 1.4+6= 5.4×2÷5.4×2=
0.35÷7= 4a+8a= 12.5×8= 2-0.65-0.35=
24.解方程。
25.列方程解答。
五、解答题
26.一辆汽车从上海到北京需15小时,平均每小时行驶全程的几分之几?已行驶9小时,还剩全程的几分之几?
27.一块梯形场地的面积是360平方米。梯形的上底是13米,下底是17米,这个梯形场地的高是多少米?(列方程解答)
28.铺两条同样长的自来水管道,第一工程队已经铺了全长的,第二工程队已经铺了全长的。哪个工程队已铺的长一些?
29.甲地与乙地之间的铁路长568千米。两列火车分别从甲、乙两地同时相对开出。从甲地开出的火车,每小时行驶77千米;从乙地开出的火车,每小时行驶65千米。经过几小时两列火车相遇?
30.五年级二班有一些学生参加“中国梦·我的梦”文艺演出。若每排4人,则多3人;若每排5人,则多4人。五年级二班至少有多少人参加文艺演出?
31.小明在装满水的玻璃瓶口放上风信子,每两天观察一次,测量芽和根的长度,并将结果制成下图。
(1)小明是第几天开始看到根、第几天开始看到芽的?
(2)和同学说说风信子芽和根的生长变化情况。
(3)你有兴趣找一种植物种子,做一次这样的实验吗?
《期中重难点检测卷-2024-2025学年数学五年级下册苏教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A C C B B C D
1.B
【分析】①条形统计图特点是用一个单位长度表示一定的数量,用直条的长短表示数量的多少,作用是从图中能清楚地看出各种数量的多少,便于相互比较。
②折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
③扇形统计图特点是以一个圆的面积表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数。清楚地看出各部分数量与总数量之间的关系。结合各统计图的特点逐项进行分析,据此解答。
【详解】A.要表示学校一年级至六年级男女生人数,选择条形统计图比较合适,不符合题意;
B.要表示第3小组记录蒜叶生长的变化情况,选择折线统计图比较合适,符合题意;
C.要表示五年级各班参加数学兴趣小组的人数,选择条形统计图比较合适,不符合题意;
D.要表示五年级6个班制作的科技作品个数,选择条形统计图比较合适,不符合题意。
故答案为:B
2.A
【分析】从左往右,第一架天平表示1个圆柱的质量+2个正方体的质量=1个长方体的质量,第二架天平表示2个圆柱的质量=1个正方体+1个长方体的质量,由此可知,1个圆柱的质量=3个正方体的质量;据此解答。
【详解】1个圆柱的质量=3个正方体的质量
2个圆柱的质量=6个正方体的质量
所以,第三架天平的右边放6个才能使天平保持平衡。
故答案为:A
3.C
【分析】个位上是0、2、4、6、8的数是2的倍数,个位上是0或5的数是5的倍数,那么个位上是0的数既是2的倍数又是5的倍数。所以,这个三位数的个位是0。十位和百位最大都只能填9,据此解题。
【详解】一个三位数,既是2的倍数又是5的倍数,这个数最大是990。
故答案为:C
4.C
【分析】设第二块菜地种的番茄是x棵,则第一块种了(x-50)棵,第三块种了(x+150)棵,根据题意可得方程:x+(x-50)+(x+150)=1000,解答求出第二块种的棵数。
【详解】解:设第二块菜地种的番茄是x棵,则第一块种了(x-50)棵,第三块种了(x+150)棵,则:
x+(x-50)+(x+150)=1000
x+x-50+x+150=1000
3x+100=1000
3x+100-100=1000-100
3x=900
3x÷3=900÷3
x=300
第二块种了300棵。
故答案为:C
5.B
【分析】两个或两个以上的合数分解质因数后,把公有的相同质因数乘起来就是最大公因数;
把公有的质因数与每个数独有质因数乘起来,就是最小公倍数。
【详解】A=2×3×5
B=2×3×7
A和B的最大公因数是:2×3=6
A和B的最小公倍数是:2×3×5×7=210
故答案为:B
6.B
【分析】观察折线统计图,一共用时120分钟,30千米用时80分钟,40千米用时120分钟,根据终点时间-起点时间=经过时间,即可求出最后10千米用的时间。
【详解】40-10=30(千米)
120-80=40(分钟)
他骑行最后10千米用了40分钟。
故答案为:B
7.C
【分析】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数;通过实际操作可知,一张圆形纸片连续对折三次后,被平均分成了8份,其中的一份就占这张圆形纸片的。
【详解】根据分析可知,将一张圆形纸片连续对折三次后平均分成一些等份,其中的一份占这张圆形纸片的。
故答案为:C
8.D
【分析】设轩轩原来有x条小鱼,则优优原来的小鱼数量是2x,根据数量关系:优优原来的小鱼数量减去6等于轩轩原来的小鱼数量加上6,据此列出方程即可。
【详解】解:设轩轩原来有x条小鱼,则优优原来的小鱼数量是2x。
如果优优送给轩轩6条,则优优现在的小鱼数量是(),轩轩现在的小鱼数量是(),他们现在的小鱼数量一样多,因此列方程是:。
故答案为:D
9. ③④⑥ ③④
【分析】等式是指用等号“=”连接的式子,方程是指含有未知数的等式。在给出的式子中:
①7+x,只是一个式子,既不是等式也不是方程。
②5x+4<28,是一个不等式,不是等式也不是方程。
③6a=48,含有未知数a且是等式,所以是方程,也是等式。
④x÷3=20,含有未知数x且是等式,所以是方程,也是等式。
⑤x-3>23,是一个不等式,不是等式也不是方程。
⑥5+10=15,是一个不含有未知数的等式。
【详解】由分析可得,等式有③、④、⑥;方程有③、④。
10. > < = >
【分析】异分母分分数比较大小,用两个分数分母的最小公倍数作公分母,然后根据分数的基本性质,把异分母分数分别化成以公分母为分母的分数,再根据同分母分数大小的比较方法,分子大的分数就大。据此解答。
【详解】
,所以
,所以
,所以
,所以
11. 2a+2 34
【分析】由“小张的邮票比小王的2倍多2张”,得出小张邮票的张数=小王邮票的张数×2+2,而小王有a张邮票,由此求出小张邮票的张数,当a=16时,代入算式计算即可。据此解答。
【详解】小张邮票的张数:2a+2(张);
当a=16时,
2a+2
=2×16+2
=32+2
=34
小张的邮票比小王的2倍多2张,如果小王有a张邮票,小张有(2a+2)张邮票;当a=16,小张有(34)张邮票。
12.7
【分析】若每个花束的康乃馨和粉百合花的朵数相同,说明康乃馨和粉百合花都是等分的,而且分的份数相同,要使每束花里花朵数最少,只要求出96和72的最大公因数,即可获得花束数,花的总数96+72除以花束数,就得到每个花束里至少有多少朵花。
【详解】96=2×2×2×2×2×3
72=2×2×2×3×3
96和72的最大公因数:2×2×2×3=24
96÷24+72÷24
=4+3
=7(朵)
每束花里至少有7朵花。
13. 1 2 4 4
【分析】所用正方形要能正好铺满长20dm、宽16dm的长方形,所用正方形的边长应为20和16的公因数,求出20和16的公因数即可;要使需要的正方形个数最少,则所用正方形的边长应最大,也就是20和16的最大公因数;据此解答。
【详解】20的因数有:1,2,4,5,10,20;
16的因数有:1,2,4,8,16;
20和16的公因数为:1,2,4,20和16的最大公因数为:4。
因此用边长1dm,2dm和4dm的正方形都能正好铺满长20dm、宽16dm的长方形,其中用4dm的正方形去铺,能使需要的正方形个数最少。
14.;
【分析】根据题意,求每支笔是铅笔总数的几分之几,就是将12支笔看作单位“1”,将其平均分成12份,其中的一份占12份的几分之几,根据分数与除法的关系可知,用除法计算;求每人分得铅笔总数的几分之几,每个人可以分得的铅笔数量占铅笔总数的几分之几,先用12除以2得到每人分得的铅笔数,再用每人分得的铅笔数除以铅笔总数即可解答。
【详解】
(支)
有12支铅笔,平均分给2个同学。每支铅笔是铅笔总数的,每人分得的铅笔是总数的。
15. 34 26
【分析】把x=22代入y=2x-10,然后求出y的值即可。把y=42代入y=2x-10,然后根据等式的性质1和2解出方程即可。
【详解】把x=22代入y=2x-10,
2×22-10
=44-10
=34(码)
把y=42代入y=2x-10,
2x-10=42
解:2x-10+10=42+10
2x=52
2x÷2=52÷2
x=26
小芳的脚长22厘米,是34码,爸爸脚长42码,是26厘米。
16.(1) 1/一 3/三
(2)上升
(3)51
【分析】(1)观察复式折线统计图,两条折线叉口最大时,表示两个车间这个月的用煤量相差最大;两条折线相交于一点时,表示两个车间这个月的用煤量相等。
(2)观察统计图中虚线的变化情况,折线向上则表示上升趋势,折线向下则表示下降趋势。
(3)先用加法求出第一车间这5个月用煤量的总吨数,再除以5,即是第一车间这5个月平均每月用煤的吨数。
【详解】(1)两个车间1月份用煤量相差最大,3月份用煤量相等。
(2)第二车间这五个月用煤量呈上升趋势。
(3)(35+40+50+60+70)÷5
=255÷5
=51(吨)
则第一车间这5个月平均每月用煤51吨。
17.×
【分析】根据等式的性质1,方程-1.7=1.7两边同时加上1.7,即可求出方程的解。
【详解】-1.7=1.7
解:-1.7+1.7=1.7+1.7
=3.4
=3.4是-1.7=1.7的解。
原题说法错误。
故答案为:×
18.√
【分析】等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
【详解】若+9=,根据等式的性质1可知,方程两边同时加上a,左右两边仍然相等,所以+9+a=+a。
故答案为:√
19.√
【分析】条形统计图能清楚地表示出数量的多少;
折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;
扇形统计图表示部分与整体之间的关系;据此解答。
【详解】为了统计商场去年各月电脑的销售数量变化情况,应选用折线统计图。
原题干说法正确。
故答案为:√
20.√
【分析】5的倍数特征:个位是0或5的数是5的倍数;每连续5个数字中,一定有末尾是0或5的数,据此判断。
【详解】个位是0或5的数是5的倍数,每连续5个数字中(0除外),一定有末尾是0或5的数,因此5个连续的自然数(0除外)中,必有一个是5的倍数,原题干的说法是正确的。
故答案为:√
21.×
【分析】带分数指的是由整数(不包括0)和真分数合成的数,所以带分数都大于1,据此解答。
【详解】整数(0除外)都可以和真分数合成带分数,原说法错误。
故答案为:×
22.√
【分析】把“1”平均分为若干份,这样的一份或几份都可以用分数来表示。其中分母表示平均分的份数,分子表示取走的份数,据此分析。
【详解】根据分数的意义,表示把单位“1”平均分成9份,取其中的2份,说法正确。
故答案为:√
23.1.89;1;7.4;4
0.05;12a;100;1
【详解】略
24.;;
;
【分析】(1)计算等式左边的加法,即可得解;
(2)先计算等式左边的乘法,再根据等式的性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时加0.6。再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以2,计算即可得解;
(3)先计算等式左边的乘法,再根据等式的性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时减30。再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以2,计算即可得解;
(4)先计算等式左边的减法,再再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以1.6,计算即可得解。
【详解】
解:
解:
解:
解:
25.39千克
【分析】根据线段图可知总共有100千克,吃掉了千克,还剩61千克。数学关系式:吃掉的千克+剩下的61千克=100千克,据此列方程解答。
【详解】
解:
吃掉了39千克。
26.;
【分析】把从上海到北京需要的总时间看作单位“1”, 把单位“1”平均分成15份,每份用分数表示为;先用除法求出已经行驶的时间占总时间的分率,再用减法计算出剩下的时间占总时间的分率,据此解答。
【详解】1÷15=
1-9÷15
=1-
=
答:平均每小时行驶全程的,还剩全程的。
27.24米
【分析】根据题意可知,设这个梯形场地的高是x米,已知梯形的面积、上底以及下底,可以根据,列出方程,再根据等式的性质解答即可。
【详解】解:设这个梯形场地的高是x米。
答:这个梯形场地的高是24米。
28.第二工程队
【分析】分别将两条水管道的全长看作单位“1”,比较两个工程队已经铺了全长的几分之几即可。异分母分数比较大小,先通分再比较。
【详解】
<
答:第二工程队已铺的长一些。
29.4小时
【分析】设经过x小时两列火车相遇,运用路程=速度×时间,分别用两列火车的速度×相遇时间,求出两列火车相遇时行驶的路程,根据数量关系:两列火车行驶的路程之和=568,据此列出方程,解方程。
【详解】解:设经过x小时两列火车相遇。
77x+65x=568
(77+65)x=568
142x=568
124x÷142=568÷142
x=4
答:经过4小时两列火车相遇。
30.19人
【分析】根据题意,每排4人,则多3人,每排5人,则多4人,可以理解为每排4人,则少1人,每排5人,则少1人,求出4和5的最小公倍数,因为4和5是互质数,所以它们的最小公倍数是它们的积,用最小公倍数再减去1,即可求出结果。
【详解】4和5的最小公倍数是4×5=20。
20-1=19(人)
答:五(2)班至少有19人参加文艺演出。
31.(1)4;6
(2)(3)见详解
【分析】(1)观察复式折线统计图,实线表示根的数据,虚线表示芽的数据,观察横轴,折线开始上升的位置是开始长根和长芽的时间;
(2)用复式折线统计图统计风信子芽和根的长度,竖轴表示长度,横轴表示天数;折线反映不同的天数根和芽的长度以及变化情况,折线的下端对应的天数就是开始看到根和芽的天数;根据折线变化情况分析风信子根和芽生长变化情况即可;
(3)可以找一种植物种子,进行一次这样的试验。
【详解】(1))答:小明是第4天开始看到根、第6天开始看到芽的。
(2)答:从图中可以看出,风信子根的生长速度要比芽快一些,这主要是因为根的生长起步较早,而芽的生长起步较迟。不过,从第10天开始根和芽的生长速度大体就相当了,这可以从折线的倾斜程度看出来,也可以从每组两个数据之间的差看出来。
(3)答:可以观察菜豆种子萌发成幼苗的过程。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中重难点检测卷-2024-2025学年数学五年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面情况中,( )比较适合用折线统计图表示。
A.学校一年级~六年级男女生人数 B.第3小组记录蒜叶生长的变化情况
C.五年级各班参加数学兴趣小组的人数 D.五年级6个班制作的科技作品个数
2.如图中前两架天平保持平衡。根据图中的等量关系,你觉得第三架天平的右边放( )个才能使天平保持平衡。
A.6 B.5 C.4 D.3
3.一个三位数,既是2的倍数又是5的倍数,这个数最大是( )。
A.998 B.995 C.990 D.999
4.王阿姨家在三块菜地里种了1000棵番茄,第一块菜地里种的番茄比第二块少50棵,第三块菜地里种的番茄比第二块多150棵。第二块菜地里种番茄( )棵。
A.450 B.350 C.300 D.250
5. A=2×3×5,B=2×3×7,那么A和B的最大公因数是( ),最小公倍数是( )。
A.10;420 B.6;210 C.210;10 D.420;6
6.李叔叔参加一项全程40千米的山地自行车赛,如图显示了不同时间他骑行的路程。他骑行最后10千米用了( )分钟。
A.10 B.40 C.20 D.60
7.将一张圆形纸片连续对折三次后平均分成一些等份,其中的一份占这张圆形纸片的( )。
A. B. C. D.
8.轩轩养的小鱼数量是优优的一半,如果优优送给轩轩6条,他们的小鱼数量就一样多了,轩轩原来有多少条小鱼?设轩轩原来有x条小鱼,列方程是( )。
A.2x-x=6 B.2x+x=6+6 C.2x+x=6 D.2x-6=x+6
二、填空题
9.在①7+x;②5x+4<28;③6a=48;④x÷3=20;⑤x-3>23;⑥5+10=15,这些式子中,等式有( )(填序号);方程有( )(填序号)。
10.在( )里填“>”“<”或“=”。
( ) ( ) ( ) ( )
11.小张的邮票比小王的2倍多2张,如果小王有a张邮票,小张有( )张邮票;当a=16,小张有( )张邮票。
12.用96朵康乃馨和72朵粉百合做成花束,每束花里的康乃馨朵数相同,粉百合朵数也相同,每束花里至少有( )朵花。
13.用边长( )dm,( )dm和( )dm的正方形都能正好铺满长20dm、宽16dm的长方形,其中用( )dm的正方形去铺,能使需要的正方形个数最少。
14.有12支铅笔,平均分给2个同学。每支铅笔是铅笔总数的,每人分得的铅笔是总数的。
15.鞋子尺码通常用“码”或“厘米”作单位,它们之间的换算关系是y=2x-10(y表示码数,x表示厘米数)。小芳的脚长22厘米,是( )码,爸爸脚长42码,是( )厘米。
16.下图是第一和第二车间1~5月份用煤情况统计,请根据图中的信息填空。
(1)两个车间( )月份用煤量相差最大,( )月份用煤量相等。
(2)第二车间这五个月用煤量呈( )趋势。
(3)第一车间这5个月平均每月用煤( )吨。
三、判断题
17.=1.7是-1.7=1.7的解。( )
18.若+9=,则+9+a=+a。( )
19.为了统计商场去年各月电脑的销售数量变化情况,应选用折线统计图。( )
20.5个连续的自然数(0除外)中,必有一个是5的倍数。( )
21.任何整数都可以和真分数合成带分数。( )
22.表示把单位“1”平均分成9份,取其中的2份。( )
四、计算题
23.口算。
2-0.11= 0.25×4= 1.4+6= 5.4×2÷5.4×2=
0.35÷7= 4a+8a= 12.5×8= 2-0.65-0.35=
24.解方程。
25.列方程解答。
五、解答题
26.一辆汽车从上海到北京需15小时,平均每小时行驶全程的几分之几?已行驶9小时,还剩全程的几分之几?
27.一块梯形场地的面积是360平方米。梯形的上底是13米,下底是17米,这个梯形场地的高是多少米?(列方程解答)
28.铺两条同样长的自来水管道,第一工程队已经铺了全长的,第二工程队已经铺了全长的。哪个工程队已铺的长一些?
29.甲地与乙地之间的铁路长568千米。两列火车分别从甲、乙两地同时相对开出。从甲地开出的火车,每小时行驶77千米;从乙地开出的火车,每小时行驶65千米。经过几小时两列火车相遇?
30.五年级二班有一些学生参加“中国梦·我的梦”文艺演出。若每排4人,则多3人;若每排5人,则多4人。五年级二班至少有多少人参加文艺演出?
31.小明在装满水的玻璃瓶口放上风信子,每两天观察一次,测量芽和根的长度,并将结果制成下图。
(1)小明是第几天开始看到根、第几天开始看到芽的?
(2)和同学说说风信子芽和根的生长变化情况。
(3)你有兴趣找一种植物种子,做一次这样的实验吗?
《期中重难点检测卷-2024-2025学年数学五年级下册苏教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A C C B B C D
1.B
【分析】①条形统计图特点是用一个单位长度表示一定的数量,用直条的长短表示数量的多少,作用是从图中能清楚地看出各种数量的多少,便于相互比较。
②折线统计图特点是用不同位置的点表示数量的多少,根据数量的多少描出各点,然后把各点用线段顺次连接起来。不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
③扇形统计图特点是以一个圆的面积表示物体的总数量,以相应的扇形面积占整个圆面积的百分数表示各有关部分占总数量的百分数。清楚地看出各部分数量与总数量之间的关系。结合各统计图的特点逐项进行分析,据此解答。
【详解】A.要表示学校一年级至六年级男女生人数,选择条形统计图比较合适,不符合题意;
B.要表示第3小组记录蒜叶生长的变化情况,选择折线统计图比较合适,符合题意;
C.要表示五年级各班参加数学兴趣小组的人数,选择条形统计图比较合适,不符合题意;
D.要表示五年级6个班制作的科技作品个数,选择条形统计图比较合适,不符合题意。
故答案为:B
2.A
【分析】从左往右,第一架天平表示1个圆柱的质量+2个正方体的质量=1个长方体的质量,第二架天平表示2个圆柱的质量=1个正方体+1个长方体的质量,由此可知,1个圆柱的质量=3个正方体的质量;据此解答。
【详解】1个圆柱的质量=3个正方体的质量
2个圆柱的质量=6个正方体的质量
所以,第三架天平的右边放6个才能使天平保持平衡。
故答案为:A
3.C
【分析】个位上是0、2、4、6、8的数是2的倍数,个位上是0或5的数是5的倍数,那么个位上是0的数既是2的倍数又是5的倍数。所以,这个三位数的个位是0。十位和百位最大都只能填9,据此解题。
【详解】一个三位数,既是2的倍数又是5的倍数,这个数最大是990。
故答案为:C
4.C
【分析】设第二块菜地种的番茄是x棵,则第一块种了(x-50)棵,第三块种了(x+150)棵,根据题意可得方程:x+(x-50)+(x+150)=1000,解答求出第二块种的棵数。
【详解】解:设第二块菜地种的番茄是x棵,则第一块种了(x-50)棵,第三块种了(x+150)棵,则:
x+(x-50)+(x+150)=1000
x+x-50+x+150=1000
3x+100=1000
3x+100-100=1000-100
3x=900
3x÷3=900÷3
x=300
第二块种了300棵。
故答案为:C
5.B
【分析】两个或两个以上的合数分解质因数后,把公有的相同质因数乘起来就是最大公因数;
把公有的质因数与每个数独有质因数乘起来,就是最小公倍数。
【详解】A=2×3×5
B=2×3×7
A和B的最大公因数是:2×3=6
A和B的最小公倍数是:2×3×5×7=210
故答案为:B
6.B
【分析】观察折线统计图,一共用时120分钟,30千米用时80分钟,40千米用时120分钟,根据终点时间-起点时间=经过时间,即可求出最后10千米用的时间。
【详解】40-10=30(千米)
120-80=40(分钟)
他骑行最后10千米用了40分钟。
故答案为:B
7.C
【分析】分数的意义:把单位“1”平均分成若干份,表示其中一份或几份的数;通过实际操作可知,一张圆形纸片连续对折三次后,被平均分成了8份,其中的一份就占这张圆形纸片的。
【详解】根据分析可知,将一张圆形纸片连续对折三次后平均分成一些等份,其中的一份占这张圆形纸片的。
故答案为:C
8.D
【分析】设轩轩原来有x条小鱼,则优优原来的小鱼数量是2x,根据数量关系:优优原来的小鱼数量减去6等于轩轩原来的小鱼数量加上6,据此列出方程即可。
【详解】解:设轩轩原来有x条小鱼,则优优原来的小鱼数量是2x。
如果优优送给轩轩6条,则优优现在的小鱼数量是(),轩轩现在的小鱼数量是(),他们现在的小鱼数量一样多,因此列方程是:。
故答案为:D
9. ③④⑥ ③④
【分析】等式是指用等号“=”连接的式子,方程是指含有未知数的等式。在给出的式子中:
①7+x,只是一个式子,既不是等式也不是方程。
②5x+4<28,是一个不等式,不是等式也不是方程。
③6a=48,含有未知数a且是等式,所以是方程,也是等式。
④x÷3=20,含有未知数x且是等式,所以是方程,也是等式。
⑤x-3>23,是一个不等式,不是等式也不是方程。
⑥5+10=15,是一个不含有未知数的等式。
【详解】由分析可得,等式有③、④、⑥;方程有③、④。
10. > < = >
【分析】异分母分分数比较大小,用两个分数分母的最小公倍数作公分母,然后根据分数的基本性质,把异分母分数分别化成以公分母为分母的分数,再根据同分母分数大小的比较方法,分子大的分数就大。据此解答。
【详解】
,所以
,所以
,所以
,所以
11. 2a+2 34
【分析】由“小张的邮票比小王的2倍多2张”,得出小张邮票的张数=小王邮票的张数×2+2,而小王有a张邮票,由此求出小张邮票的张数,当a=16时,代入算式计算即可。据此解答。
【详解】小张邮票的张数:2a+2(张);
当a=16时,
2a+2
=2×16+2
=32+2
=34
小张的邮票比小王的2倍多2张,如果小王有a张邮票,小张有(2a+2)张邮票;当a=16,小张有(34)张邮票。
12.7
【分析】若每个花束的康乃馨和粉百合花的朵数相同,说明康乃馨和粉百合花都是等分的,而且分的份数相同,要使每束花里花朵数最少,只要求出96和72的最大公因数,即可获得花束数,花的总数96+72除以花束数,就得到每个花束里至少有多少朵花。
【详解】96=2×2×2×2×2×3
72=2×2×2×3×3
96和72的最大公因数:2×2×2×3=24
96÷24+72÷24
=4+3
=7(朵)
每束花里至少有7朵花。
13. 1 2 4 4
【分析】所用正方形要能正好铺满长20dm、宽16dm的长方形,所用正方形的边长应为20和16的公因数,求出20和16的公因数即可;要使需要的正方形个数最少,则所用正方形的边长应最大,也就是20和16的最大公因数;据此解答。
【详解】20的因数有:1,2,4,5,10,20;
16的因数有:1,2,4,8,16;
20和16的公因数为:1,2,4,20和16的最大公因数为:4。
因此用边长1dm,2dm和4dm的正方形都能正好铺满长20dm、宽16dm的长方形,其中用4dm的正方形去铺,能使需要的正方形个数最少。
14.;
【分析】根据题意,求每支笔是铅笔总数的几分之几,就是将12支笔看作单位“1”,将其平均分成12份,其中的一份占12份的几分之几,根据分数与除法的关系可知,用除法计算;求每人分得铅笔总数的几分之几,每个人可以分得的铅笔数量占铅笔总数的几分之几,先用12除以2得到每人分得的铅笔数,再用每人分得的铅笔数除以铅笔总数即可解答。
【详解】
(支)
有12支铅笔,平均分给2个同学。每支铅笔是铅笔总数的,每人分得的铅笔是总数的。
15. 34 26
【分析】把x=22代入y=2x-10,然后求出y的值即可。把y=42代入y=2x-10,然后根据等式的性质1和2解出方程即可。
【详解】把x=22代入y=2x-10,
2×22-10
=44-10
=34(码)
把y=42代入y=2x-10,
2x-10=42
解:2x-10+10=42+10
2x=52
2x÷2=52÷2
x=26
小芳的脚长22厘米,是34码,爸爸脚长42码,是26厘米。
16.(1) 1/一 3/三
(2)上升
(3)51
【分析】(1)观察复式折线统计图,两条折线叉口最大时,表示两个车间这个月的用煤量相差最大;两条折线相交于一点时,表示两个车间这个月的用煤量相等。
(2)观察统计图中虚线的变化情况,折线向上则表示上升趋势,折线向下则表示下降趋势。
(3)先用加法求出第一车间这5个月用煤量的总吨数,再除以5,即是第一车间这5个月平均每月用煤的吨数。
【详解】(1)两个车间1月份用煤量相差最大,3月份用煤量相等。
(2)第二车间这五个月用煤量呈上升趋势。
(3)(35+40+50+60+70)÷5
=255÷5
=51(吨)
则第一车间这5个月平均每月用煤51吨。
17.×
【分析】根据等式的性质1,方程-1.7=1.7两边同时加上1.7,即可求出方程的解。
【详解】-1.7=1.7
解:-1.7+1.7=1.7+1.7
=3.4
=3.4是-1.7=1.7的解。
原题说法错误。
故答案为:×
18.√
【分析】等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
【详解】若+9=,根据等式的性质1可知,方程两边同时加上a,左右两边仍然相等,所以+9+a=+a。
故答案为:√
19.√
【分析】条形统计图能清楚地表示出数量的多少;
折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;
扇形统计图表示部分与整体之间的关系;据此解答。
【详解】为了统计商场去年各月电脑的销售数量变化情况,应选用折线统计图。
原题干说法正确。
故答案为:√
20.√
【分析】5的倍数特征:个位是0或5的数是5的倍数;每连续5个数字中,一定有末尾是0或5的数,据此判断。
【详解】个位是0或5的数是5的倍数,每连续5个数字中(0除外),一定有末尾是0或5的数,因此5个连续的自然数(0除外)中,必有一个是5的倍数,原题干的说法是正确的。
故答案为:√
21.×
【分析】带分数指的是由整数(不包括0)和真分数合成的数,所以带分数都大于1,据此解答。
【详解】整数(0除外)都可以和真分数合成带分数,原说法错误。
故答案为:×
22.√
【分析】把“1”平均分为若干份,这样的一份或几份都可以用分数来表示。其中分母表示平均分的份数,分子表示取走的份数,据此分析。
【详解】根据分数的意义,表示把单位“1”平均分成9份,取其中的2份,说法正确。
故答案为:√
23.1.89;1;7.4;4
0.05;12a;100;1
【详解】略
24.;;
;
【分析】(1)计算等式左边的加法,即可得解;
(2)先计算等式左边的乘法,再根据等式的性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时加0.6。再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以2,计算即可得解;
(3)先计算等式左边的乘法,再根据等式的性质1:等式的左右两边同时加上(或减去)同一个数,等式仍然成立,等式两边同时减30。再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以2,计算即可得解;
(4)先计算等式左边的减法,再再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立,等式两边同时除以1.6,计算即可得解。
【详解】
解:
解:
解:
解:
25.39千克
【分析】根据线段图可知总共有100千克,吃掉了千克,还剩61千克。数学关系式:吃掉的千克+剩下的61千克=100千克,据此列方程解答。
【详解】
解:
吃掉了39千克。
26.;
【分析】把从上海到北京需要的总时间看作单位“1”, 把单位“1”平均分成15份,每份用分数表示为;先用除法求出已经行驶的时间占总时间的分率,再用减法计算出剩下的时间占总时间的分率,据此解答。
【详解】1÷15=
1-9÷15
=1-
=
答:平均每小时行驶全程的,还剩全程的。
27.24米
【分析】根据题意可知,设这个梯形场地的高是x米,已知梯形的面积、上底以及下底,可以根据,列出方程,再根据等式的性质解答即可。
【详解】解:设这个梯形场地的高是x米。
答:这个梯形场地的高是24米。
28.第二工程队
【分析】分别将两条水管道的全长看作单位“1”,比较两个工程队已经铺了全长的几分之几即可。异分母分数比较大小,先通分再比较。
【详解】
<
答:第二工程队已铺的长一些。
29.4小时
【分析】设经过x小时两列火车相遇,运用路程=速度×时间,分别用两列火车的速度×相遇时间,求出两列火车相遇时行驶的路程,根据数量关系:两列火车行驶的路程之和=568,据此列出方程,解方程。
【详解】解:设经过x小时两列火车相遇。
77x+65x=568
(77+65)x=568
142x=568
124x÷142=568÷142
x=4
答:经过4小时两列火车相遇。
30.19人
【分析】根据题意,每排4人,则多3人,每排5人,则多4人,可以理解为每排4人,则少1人,每排5人,则少1人,求出4和5的最小公倍数,因为4和5是互质数,所以它们的最小公倍数是它们的积,用最小公倍数再减去1,即可求出结果。
【详解】4和5的最小公倍数是4×5=20。
20-1=19(人)
答:五(2)班至少有19人参加文艺演出。
31.(1)4;6
(2)(3)见详解
【分析】(1)观察复式折线统计图,实线表示根的数据,虚线表示芽的数据,观察横轴,折线开始上升的位置是开始长根和长芽的时间;
(2)用复式折线统计图统计风信子芽和根的长度,竖轴表示长度,横轴表示天数;折线反映不同的天数根和芽的长度以及变化情况,折线的下端对应的天数就是开始看到根和芽的天数;根据折线变化情况分析风信子根和芽生长变化情况即可;
(3)可以找一种植物种子,进行一次这样的试验。
【详解】(1))答:小明是第4天开始看到根、第6天开始看到芽的。
(2)答:从图中可以看出,风信子根的生长速度要比芽快一些,这主要是因为根的生长起步较早,而芽的生长起步较迟。不过,从第10天开始根和芽的生长速度大体就相当了,这可以从折线的倾斜程度看出来,也可以从每组两个数据之间的差看出来。
(3)答:可以观察菜豆种子萌发成幼苗的过程。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
