板块一 点的移动规律培优练习 (含答案)
文档属性
| 名称 | 板块一 点的移动规律培优练习 (含答案) | 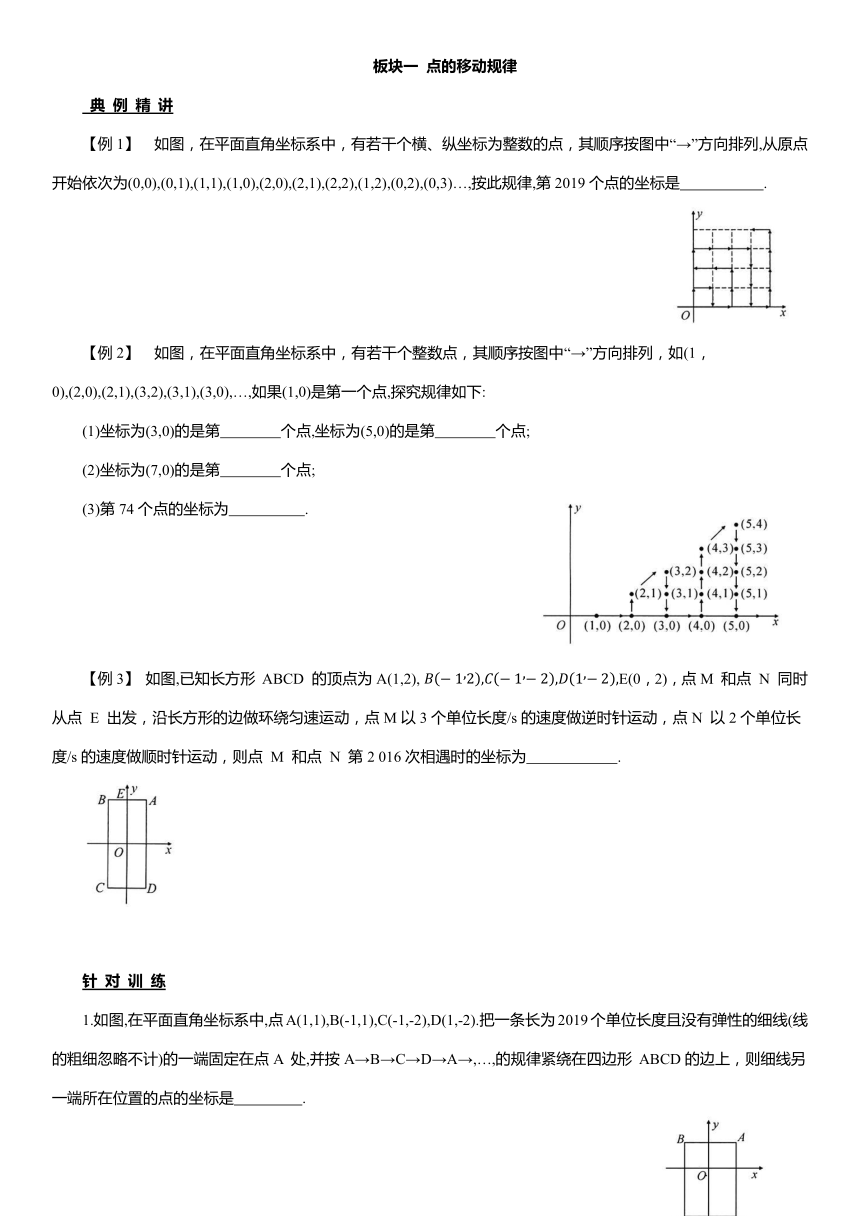 | |
| 格式 | docx | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 05:33:40 | ||
图片预览


文档简介
板块一 点的移动规律
典 例 精 讲
【例1】 如图,在平面直角坐标系中,有若干个横、纵坐标为整数的点,其顺序按图中“→”方向排列,从原点开始依次为(0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3)…,按此规律,第2019个点的坐标是 .
【例2】 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,如果(1,0)是第一个点,探究规律如下:
(1)坐标为(3,0)的是第 个点,坐标为(5,0)的是第 个点;
(2)坐标为(7,0)的是第 个点;
(3)第74个点的坐标为 .
【例3】 如图,已知长方形 ABCD 的顶点为A(1,2), E(0,2),点M 和点 N 同时从点 E 出发,沿长方形的边做环绕匀速运动,点M以3个单位长度/s的速度做逆时针运动,点N 以2个单位长度/s的速度做顺时针运动,则点 M 和点 N 第2 016次相遇时的坐标为 .
针 对 训 练
1.如图,在平面直角坐标系中,点A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A 处,并按A→B→C→D→A→,…,的规律紧绕在四边形 ABCD的边上,则细线另一端所在位置的点的坐标是 .
2.在平面直角坐标系中,小明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位长度,第2步向右走2个单位长度,第3步向上走1个单位长度,第4步向右走1个单位长度,………,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位长度;当n被3除,余数为1时,则向右走1个单位长度;当n被3除,余数为2时,则向右走2个单位长度,当走完第100步时,棋子所处位置的坐标是( )
A.(66,34) B.(67,33) C.(100,33) D.(99,34)
3.在平面直角坐标系中,点A(1,0)第一次向左跳动至A (-1,1),第二次向右跳至 A (2,1),第三次向左跳至A (-2,2),第四次向右跳至A (3,2),……,依照此规律跳动下去,点A第2020次跳动后至 A 的坐标是( )
A.(-1 011,1011) B.(1 011,1 010) C.(-1 010,1 010) D.(1010,1009)
4.如图,在平面直角坐标系中,一个点从 A(a ,a ){出发,沿图中路线依次经过B(a ,a ),C(a ,a ),D(a ,a ),…,按此规律一直运动下去,则 的值为( )
A.1 007 B.1 009
C.1 511 D.1514
5.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1),…,根据这个规律探索可得,第100个点的坐标为( )
A.(14,0) B.(14,-1)
C.(14,1) D.(14,2)
6.如图,长方形 BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点 A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度/秒匀速运动,物体乙按顺时针方向以2个单位长度/秒匀速运动,则两个物体运动后的第2002次相遇地点的坐标是( )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
第6讲 坐标与规律
板块一 点的移动规律
典 例 精 讲
【例1】 如图,在平面直角坐标系中,有若干个横、纵坐标为整数的点,其顺序按图中“→”方向排列,从原点开始依次为(0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3)…,按此规律,第2019个点的坐标是 (6,44) .
【解答】第一个正方形上有4个点,添上第二个正方形后,一共有3×3=9个点,添上第三个正方形后,一共有4×4=16个点,∵添上第44个正方形后,一共有45×45=2025个点,∴第2019个点应在第44个正方形上,第44个正方形最后的那个数的坐标为(0,44),减去6个数即是第2019个数,故答案为(6,44).
【例2】 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,如果(1,0)是第一个点,探究规律如下:
(1)坐标为(3,0)的是第 6 个点,坐标为(5,0)的是第 15 个点;
(2)坐标为(7,0)的是第 28 个点;
(3)第74个点的坐标为 (12,7) .
【解答】(1)由图可知,坐标为(3,0)的点是第1+2+3=6个点,坐标是(5,0)的点是第1+2+3+4+5=15个点,故答案为:6,15;
(2)坐标为(7,0)的点是第1+2+3+4+5+6+7=28个点,故答案为:28;
(3)∵(11,0)是第1+2+3+…+11=66个点,(12,11)是第1+2+3+…+12=78个点,∴第74个点是(12,7),故答案为:(12,7).
【例3】 如图,已知长方形 ABCD的顶点为A(1,2),B(-1,2),C(-1,-2),D(1,-2),E(0,2),点M 和点 N 同时从点 E 出发,沿长方形的边做环绕匀速运动,点M以3个单位长度/s的速度做逆时针运动,点N 以2个单位长度/s的速度做顺时针运动,则点 M 和点 N 第2 016次相遇时的坐标为
【解答】∵A(1,2),B(-1,2),C(-1,-2),D(1,-2),∴AB=2,BC=4.
设点M 和点N 第2016次相遇时的时间为x,根据题意,得(3+2)x=2016×2×(4+2),解得 ∴点 M 和点N 第2016次相遇时,点 N 走过的路程为
∵长方形ABCD的周长为12,
∴点M 和点 N 第2016次相遇时的位置在距离点N顺时针方向的 个单位长度.
∴相遇点的坐标为
针 对 训 练
1.如图,在平面直角坐标系中,点A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 A 处,并按A→B→C→D→A→,…,的规律紧绕在四边形 ABCD的边上,则细线另一端所在位置的点的坐标是 (1,0) .
2.在平面直角坐标系中,小明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位长度,第2步向右走2个单位长度,第3步向上走1个单位长度,第4步向右走1个单位长度,……,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位长度;当n被3除,余数为1时,则向右走1个单位长度;当n被3除,余数为2时,则向右走2个单位长度,当走完第100步时,棋子所处位置的坐标是( C )
A.(66,34) B.(67,33) C.(100,33) D.(99,34)
3.在平面直角坐标系中,点A(1,0)第一次向左跳动至 A (-1,1),第二次向右跳至 A (2,1),第三次向左跳至A (-2,2),第四次向右跳至A (3,2),……,依照此规律跳动下去,点A第2020次跳动后至 A 的坐标是( B )
A.(-1 011,1 011) B.(1 011,1010) C.(-1 010,1 010) D.(1010,1009)
4.如图,在平面直角坐标系中,一个点从A(a ,a )出发,沿图中路线依次经过B(a ,a ),C(a ,a ),D(a ,a ),…,按此规律一直运动下去,则a 018 + 的值为( D )
A.1 007 B.1 009
C.1 511 D.1514
5.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1),…,根据这个规律探索可得,第100个点的坐标为( D )
A.(14,0) B.(14,-1)
C.(14,1) D.(14,2)
6.如图,长方形 BCDE 的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度/秒匀速运动,物体乙按顺时针方向以2个单位长度/秒匀速运动,则两个物体运动后的第2002次相遇地点的坐标是( B )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
【解答】设每t秒相遇1次,∵C长方形BCDE =12,∴(1+2)t=2002×12,∴t=8008(秒),
∴甲共行走8008×1=8008(个单位长度), 圈,
个单位长度,
∴甲到达(-1,1).
典 例 精 讲
【例1】 如图,在平面直角坐标系中,有若干个横、纵坐标为整数的点,其顺序按图中“→”方向排列,从原点开始依次为(0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3)…,按此规律,第2019个点的坐标是 .
【例2】 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,如果(1,0)是第一个点,探究规律如下:
(1)坐标为(3,0)的是第 个点,坐标为(5,0)的是第 个点;
(2)坐标为(7,0)的是第 个点;
(3)第74个点的坐标为 .
【例3】 如图,已知长方形 ABCD 的顶点为A(1,2), E(0,2),点M 和点 N 同时从点 E 出发,沿长方形的边做环绕匀速运动,点M以3个单位长度/s的速度做逆时针运动,点N 以2个单位长度/s的速度做顺时针运动,则点 M 和点 N 第2 016次相遇时的坐标为 .
针 对 训 练
1.如图,在平面直角坐标系中,点A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A 处,并按A→B→C→D→A→,…,的规律紧绕在四边形 ABCD的边上,则细线另一端所在位置的点的坐标是 .
2.在平面直角坐标系中,小明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位长度,第2步向右走2个单位长度,第3步向上走1个单位长度,第4步向右走1个单位长度,………,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位长度;当n被3除,余数为1时,则向右走1个单位长度;当n被3除,余数为2时,则向右走2个单位长度,当走完第100步时,棋子所处位置的坐标是( )
A.(66,34) B.(67,33) C.(100,33) D.(99,34)
3.在平面直角坐标系中,点A(1,0)第一次向左跳动至A (-1,1),第二次向右跳至 A (2,1),第三次向左跳至A (-2,2),第四次向右跳至A (3,2),……,依照此规律跳动下去,点A第2020次跳动后至 A 的坐标是( )
A.(-1 011,1011) B.(1 011,1 010) C.(-1 010,1 010) D.(1010,1009)
4.如图,在平面直角坐标系中,一个点从 A(a ,a ){出发,沿图中路线依次经过B(a ,a ),C(a ,a ),D(a ,a ),…,按此规律一直运动下去,则 的值为( )
A.1 007 B.1 009
C.1 511 D.1514
5.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1),…,根据这个规律探索可得,第100个点的坐标为( )
A.(14,0) B.(14,-1)
C.(14,1) D.(14,2)
6.如图,长方形 BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点 A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度/秒匀速运动,物体乙按顺时针方向以2个单位长度/秒匀速运动,则两个物体运动后的第2002次相遇地点的坐标是( )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
第6讲 坐标与规律
板块一 点的移动规律
典 例 精 讲
【例1】 如图,在平面直角坐标系中,有若干个横、纵坐标为整数的点,其顺序按图中“→”方向排列,从原点开始依次为(0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3)…,按此规律,第2019个点的坐标是 (6,44) .
【解答】第一个正方形上有4个点,添上第二个正方形后,一共有3×3=9个点,添上第三个正方形后,一共有4×4=16个点,∵添上第44个正方形后,一共有45×45=2025个点,∴第2019个点应在第44个正方形上,第44个正方形最后的那个数的坐标为(0,44),减去6个数即是第2019个数,故答案为(6,44).
【例2】 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,如果(1,0)是第一个点,探究规律如下:
(1)坐标为(3,0)的是第 6 个点,坐标为(5,0)的是第 15 个点;
(2)坐标为(7,0)的是第 28 个点;
(3)第74个点的坐标为 (12,7) .
【解答】(1)由图可知,坐标为(3,0)的点是第1+2+3=6个点,坐标是(5,0)的点是第1+2+3+4+5=15个点,故答案为:6,15;
(2)坐标为(7,0)的点是第1+2+3+4+5+6+7=28个点,故答案为:28;
(3)∵(11,0)是第1+2+3+…+11=66个点,(12,11)是第1+2+3+…+12=78个点,∴第74个点是(12,7),故答案为:(12,7).
【例3】 如图,已知长方形 ABCD的顶点为A(1,2),B(-1,2),C(-1,-2),D(1,-2),E(0,2),点M 和点 N 同时从点 E 出发,沿长方形的边做环绕匀速运动,点M以3个单位长度/s的速度做逆时针运动,点N 以2个单位长度/s的速度做顺时针运动,则点 M 和点 N 第2 016次相遇时的坐标为
【解答】∵A(1,2),B(-1,2),C(-1,-2),D(1,-2),∴AB=2,BC=4.
设点M 和点N 第2016次相遇时的时间为x,根据题意,得(3+2)x=2016×2×(4+2),解得 ∴点 M 和点N 第2016次相遇时,点 N 走过的路程为
∵长方形ABCD的周长为12,
∴点M 和点 N 第2016次相遇时的位置在距离点N顺时针方向的 个单位长度.
∴相遇点的坐标为
针 对 训 练
1.如图,在平面直角坐标系中,点A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 A 处,并按A→B→C→D→A→,…,的规律紧绕在四边形 ABCD的边上,则细线另一端所在位置的点的坐标是 (1,0) .
2.在平面直角坐标系中,小明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位长度,第2步向右走2个单位长度,第3步向上走1个单位长度,第4步向右走1个单位长度,……,依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位长度;当n被3除,余数为1时,则向右走1个单位长度;当n被3除,余数为2时,则向右走2个单位长度,当走完第100步时,棋子所处位置的坐标是( C )
A.(66,34) B.(67,33) C.(100,33) D.(99,34)
3.在平面直角坐标系中,点A(1,0)第一次向左跳动至 A (-1,1),第二次向右跳至 A (2,1),第三次向左跳至A (-2,2),第四次向右跳至A (3,2),……,依照此规律跳动下去,点A第2020次跳动后至 A 的坐标是( B )
A.(-1 011,1 011) B.(1 011,1010) C.(-1 010,1 010) D.(1010,1009)
4.如图,在平面直角坐标系中,一个点从A(a ,a )出发,沿图中路线依次经过B(a ,a ),C(a ,a ),D(a ,a ),…,按此规律一直运动下去,则a 018 + 的值为( D )
A.1 007 B.1 009
C.1 511 D.1514
5.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1),…,根据这个规律探索可得,第100个点的坐标为( D )
A.(14,0) B.(14,-1)
C.(14,1) D.(14,2)
6.如图,长方形 BCDE 的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度/秒匀速运动,物体乙按顺时针方向以2个单位长度/秒匀速运动,则两个物体运动后的第2002次相遇地点的坐标是( B )
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
【解答】设每t秒相遇1次,∵C长方形BCDE =12,∴(1+2)t=2002×12,∴t=8008(秒),
∴甲共行走8008×1=8008(个单位长度), 圈,
个单位长度,
∴甲到达(-1,1).
同课章节目录
