第十一章反比例函数同步练习（含解析）

中小学教育资源及组卷应用平台
第十一章反比例函数
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．已知点，，都在反比例函数的图象上，并且，则下列结论正确的是（ ）
A． B． C． D．
2．如图，在平面直角坐标系中有，，，四个点，其中恰有三点在反比例函数的图象上．根据图中四点的位置，判断这四个点中不在函数的图象上的点是（ ）
A．点 B．点 C．点 D．点
3．物体所受的压力F（N）与所受的压强P（Pa）及受力面积S（m2）满足关系式为P×S＝F（S≠0），当压力F（N）一定时，P与S的图象大致是（　　）
A． B． C． D．
4．如图，△ABC的三个顶点分别为A(1，2)、B(4，2)、C(4，4)．若反比例函数y＝在第一象限内的图象与△ABC有交点，则k的取值范围是(　　)
A．1≤k≤4 B．2≤k≤8 C．2≤k≤16 D．8≤k≤16
5．下列函数中，为反比例函数的是（　　）
A．y＝x B．y＝ C．y＝－5x－2 D．y＝－x－1
6．已知一次函数的图象如图，那么正比例函数和反比例函数在同一坐标系中的图象大致是（ ）

A． B． C． D．
7．如图，在平面直角坐标系中，点P在反比例函数（，）的图象上，其纵坐标为2，过点P作//轴，交x轴于点Q，将线段绕点Q顺时针旋转60°得到线段．若点M也在该反比例函数的图象上，则k的值为（ ）
A． B． C． D．4
8．已知反比例函数，当时，有（ ）
A．最小值 B．最大值 C．最小值 D．最大值
9．若函数是反比例函数，的值是（　　）
A． B．1 C． D．不能确定
10．在平面直角坐标系中，已知反比例函数满足：当时，y随x的增大而减小．若该反比例函数的图像与直线都经过点P，且，则实数k=（ ）
A． B． C． D．
11．某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度（微克/毫升）与服药时间小时之间函数关系如图所示（当时，与成反比例）．血液中药物浓度不低于微克毫升的持续时间为（ ）
A． B． C． D．
12．如图，反比例函数的图象的一个分支上有一点，平行于轴，交轴于点，的面积是，则反比例函数的表达式是（　　）

A． B． C．或 D．
二、填空题
13．如图，点A是双曲线在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为 ．
14．已知反比例函数，当时，y的取值范围为 .
15．已知关于x的反比例函数，则m的值为 ．
16．函数的图象的两个分支在第 象限；在每个象限y都随x的增大而 .
17．如图，平行四边形ABCD中，顶点A的坐标是（0，2），AD//x轴，BC交y轴于点E，点E的纵坐标是﹣4，平行四边形ABCD的面积是24，反比例函数y＝的图象经过点B和D．则k＝ ．

三、解答题
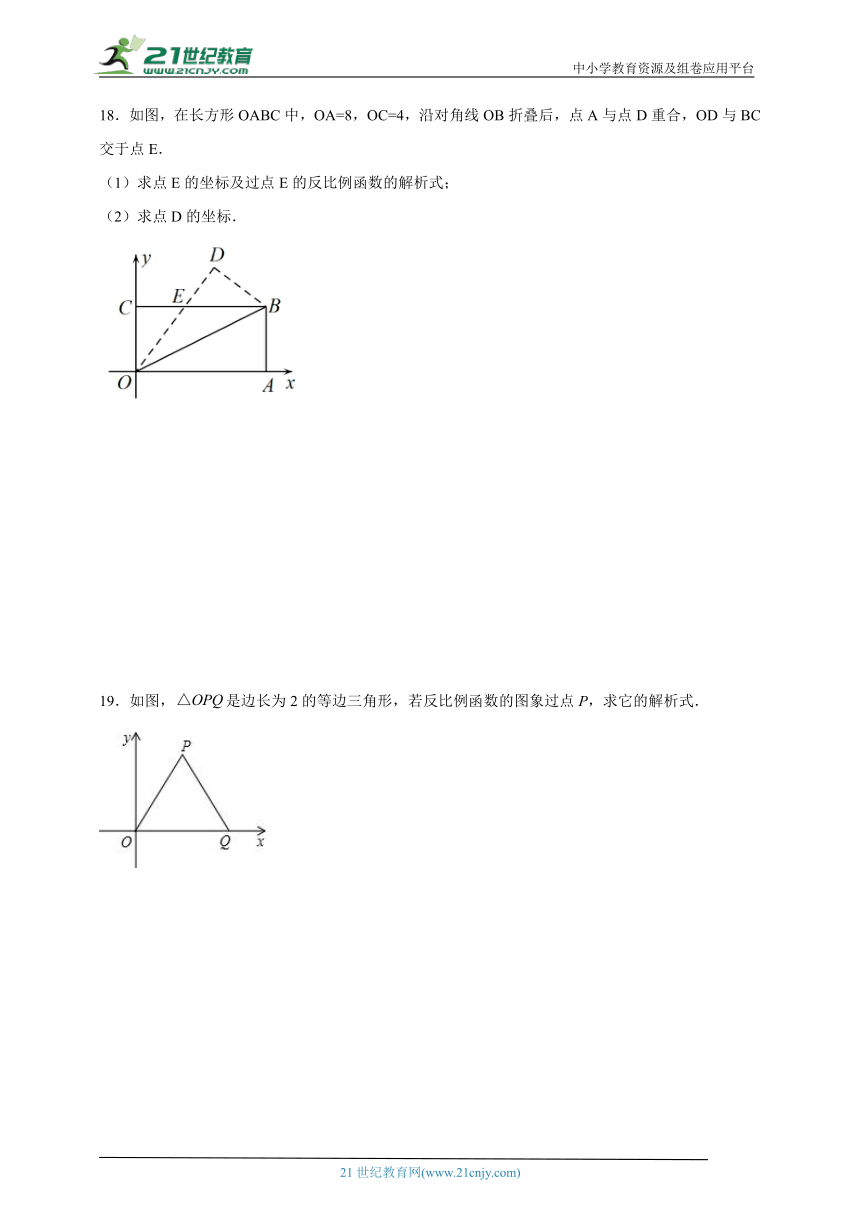
18．如图，在长方形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E．
（1）求点E的坐标及过点E的反比例函数的解析式；
（2）求点D的坐标．
19．如图，是边长为2的等边三角形，若反比例函数的图象过点P，求它的解析式．
20．如图，点在反比例函数的图象上，点B在y轴上，，将线段向右下方平移，得到线段，此时点C落在反比例函数的图象上，点D落在x轴正半轴上，且．
(1)点B的坐标为__________，点D的坐标为__________，点C的坐标为__________（用含m的式子表示）；
(2)求k的值和直线的表达式．
21．如图，函数的图象过和两点．
(1)求n和k的值．
(2)将直线沿x轴向左移动得直线，交x轴于点D，交y轴于点E，交的图象于点C，若，求直线的解析式．
(3)在（2）的条件下，第二象限内是否存在点F，使得为等腰直角三角形？若存在，请直接写出点F的坐标；若不存在，请说明理由．
22．已知反比例函数的图象过点．
求这个反比例函数的表达式；
这个函数的图象分布在哪些象限？随的增大如何变化？
点，和是否在这个函数的图象上？
23．如图，科技小组准备用材料围建一个面积为60ｍ2的矩形科技园ABCD，其中一边AB靠墙，墙长为．设AD的长为，DC的长为．

（1）求与之间的函数关系式；
（2）若围成矩形科技园ABCD的三边材料总长不超过26ｍ，材料AD和DC的长都是整米数，求出满足条件的所有围建方案．
24．已知图中的曲线是反比例函数y＝（m为常数）图象的一支．
（1）根据图象位置，求m的取值范围；
（2）若该函数的图象任取一点A，过A点作x轴的垂线，垂足为B，当△OAB的面积为4时，求m的值．

《第十一章反比例函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C C C D C C B A B
题号 11 12
答案 A B
1．C
【分析】根据题意可得图象位于第二、四象限内，且在每一象限内，y随x的增大而增大，即可求解．
【详解】解：∵点，，都在反比例函数的图象上，
∴图象位于第二、四象限内，且在每一象限内，y随x的增大而增大，
∵，
∴点，位于第四象限内，点位于第二象限内，
∴．
故选：C．
【点睛】本题主要考查了反比例函数的图象和性质，熟练掌握反比例函数的图象和性质是解题的关键．
2．C
【分析】根据反比例函数的性质，在第一象限内随的增大而减小，用平滑的曲线连接发现点不在函数的图象上
【详解】解：在第一象限内随的增大而减小，用平滑的曲线连接发现点不在函数的图象上
故选C
【点睛】本题考查了反比例函数的性质，掌握反比例数图象的性质是解题的关键．
3．C
【分析】利用压强公式得到P=,则可判定P与S为反比例函数关系,然后利用S的取值范围可对各选项进行判断.
【详解】解:P=,
所以P与S为反比例函数关系,
因为S>0,
所以反比例函数图象在第一象限.
所以C选项是正确的.
【点睛】本题主要考查反比例函数的应用，解题关键在于确定两个变量之间的函数关系.
4．C
【详解】试题解析：由于△ABC是直角三角形，所以当反比例函数经过点A时k最小，进过点C时k最大，据此可得出结论．
∵△ABC是直角三角形，∴当反比例函数经过点A时k最小，经过点C时k最大，
∴k最小=1×2=2，k最大=4×4=16，∴2≤k≤16．故选C．
5．D
【分析】根据反比例函数的定义逐项分析即可．
【详解】解：A． y＝x是正比例函数，不符合题意；
B． y＝不是反比例函数，不符合题意；
C． y＝－5x－2不是反比例函数，不符合题意；
D． y＝－x－1是反比例函数，符合题意；
故选：D．
【点睛】本题考查了反比例函数的定义，解题的关键是掌握一般地，形如（k为常数，k≠0）的函数叫做反比例函数．
6．C
【分析】根据一次函数的图象所在象限，可得的取值范围，据此即可求解．
【详解】解：如图所示，∵一次函数的图象经过第二、三、四象限，
∴．
∴正比例函数的图象经过第二、四象限，
反比例函数的图象经过第二、四象限．
综上所述，符合条件的图象是C选项．
故选：C．
【点睛】本题考查了通过一次函数的图象求解系数的范围、反比例函数的图象等．掌握相关结论是解题关键．
7．C
【分析】作MN⊥x轴交于点N，分别表示出ON、MN，利用k值的几何意义列式即可求出结果．
【详解】解：作MN⊥x轴交于点N，如图所示，
∵P点纵坐标为：2，
∴P点坐标表示为：（，2），PQ=2，
由旋转可知：QM=PQ=2，∠PQM=60°，
∴∠MQN=30°，
∴MN=，QN=，
∴，
即：，
解得：k=，
故选：C．
【点睛】本题主要考查的是k的几何意义，表示出对应线段是解题的关键．
8．B
【分析】根据反比例函数的，可知函数图像经过第二、四象限，由此即可求解．
【详解】解：反比例函数中，，
∴函数图像经过第二、四象限，如图所示，
当时，看第二象限中的函数图像可知，有最大值，即，
故选：．
【点睛】本题主要考查反比例函数图像，理解并掌握反比例函数的值大小与图像的特点是解题的关键．
9．A
【分析】本题考查的是反比例函数的定义，熟知反比例函数的定义是解题的关键．根据反比例函数的定义求出的值即可．
【详解】∵是反比例函数，
∴，
解得．
故选：A
10．B
【分析】设，根据题意，得，结合当时，y随x的增大而减小，判定，计算取舍即可．
【详解】设，根据题意，得，
所以，
解得，
因为当时，y随x的增大而减小，
所以，
所以舍去，
故选B．
【点睛】本题考查了一次函数与反比例函数的交点，勾股定理，完全平方公式的应用，熟练掌握交点坐标的意义是解题的关键．
11．A
【分析】先分别利用正比例函数以及反比例函数解析式，再利用y＝6分别得出x的值，进而得出答案．
【详解】解：当0≤x≤4时，设直线解析式为：y＝kx，
将（4，8）代入得：8＝4k，
解得：k＝2，
故直线解析式为：y＝2x，
当4≤x≤10时，设反比例函数解析式为：y＝，
将（4，8）代入得：8＝，
解得：a＝32，
故反比例函数解析式为：y＝；
因此血液中药物浓度上升阶段的函数关系式为y＝2x（0≤x≤4），
下降阶段的函数关系式为y＝（4≤x≤10）．
当y＝6，则6＝2x，解得：x＝3，
当y＝6，则6＝，解得：x＝，
∵ 3＝（小时），
∴血液中药物浓度不低于6微克/毫升的持续时间小时
故选A．
【点睛】此题主要考查了反比例函数的应用，根据题意得出函数解析式是解题关键．
12．B
【分析】此题考查了反比例函数系数的几何意义，由轴可得为直角三角形，进而由的面积是，得到，即得或，再根据函数的图象位于第一象限可得，即可得到，据此可求解，掌握反比例函数的性质是解题的关键．
【详解】解：∵轴，
∴轴，
∴，
∴为直角三角形，
∵的面积是，
∴，
∴或，
∵函数图象的一个分支位于第一象限，
∴，
∴，
∴反比例函数表达式为，
故选：．
13．y=-
【分析】连结OC，作CD⊥x轴于D，AE⊥x轴于E，如图，设A点坐标为，再证明△COD≌△OAE（AAS），表示C点坐标为，从而可得答案.
【详解】解：连结OC，作CD⊥x轴于D，AE⊥x轴于E，如图，
设A点坐标为，
∵A点、B点是正比例函数图象与双曲线的交点，
∴点A与点B关于原点对称，
∴OA=OB
∵△ABC为等腰直角三角形，
∴OC=OA，OC⊥OA，
∴∠DOC+∠AOE=90°，
∵∠DOC+∠DCO=90°，
∴∠DCO=∠AOE，
∵在△COD和△OAE中
∴△COD≌△OAE（AAS），
∴OD=AE=，CD=OE=a，
∴C点坐标为，
∵，
∴点C在反比例函数图象上．
故答案为：
【点睛】本题考查的是等腰直角三角形的性质，三角形全等的判定与性质，反比例函数的图象与性质，利用三角形的全等确定的坐标是解本题的关键.
14．
【分析】直接根据反比例函数的图象进行解答即可．
【详解】解：∵当时，.
∴反比例函数的图象位于第一、三象限，在每个象限内，y随x的增大而减小，
∴y的取值范围是.
故答案为.
【点睛】本题主要考查反比例函数的性质，掌握反比例函数的增减性是解题的关键．
15．
【分析】根据反比例函数的定义得到，，即可求得m的值．
【详解】解：∵是反比例函数，
∴，，
∴且，
∴，
故答案为：
【点睛】此题考查了反比例函数，形如的函数是反比例函数，熟练掌握反比例函数的定义是解题的关键．
16． 一、三 减小
【分析】反比例函数的图象是双曲线，根据比例系数可得图象分布在哪两个象限，进而可得函数的增减性．
【详解】解：所有反比例函数的图象都是双曲线；
∵比例系数为4，
∴分布在一、三象限，在每个象限内，y都随x的增大而减小．
故答案为(1). 一、三 (2). 减小
【点睛】本题考查反比例函数的图象的性质；解题关键是掌握：所有反比例函数的图象都是双曲线；反比例函数的比例系数小于0，函数的两个分支分布在二、四象限，在每个象限内，y都随x的增大而增大；反比例函数的比例系数大于0，函数的两个分支分布在一、三象限，在每个象限内，y都随x的增大而减小.
17．8
【分析】根据题意得出AE＝6，结合平行四边形的面积得出AD＝BC＝4，继而知点D坐标，从而得出反比例函数解析式．
【详解】解：∵顶点A的坐标是（0，2），
∴OA＝2，
∵点E的纵坐标是﹣4，
∴OE＝4，
∴AE＝6，
又的面积是24，
∴AD＝BC＝4，
∵AD//x轴，
∴D（4，2）
∵反比例函数的图象经过点D，
∴k＝4×2＝8，
故答案为：8．
【点睛】本题考查的是平行四边形的性质，利用待定系数法求解反比例函数的解析式，掌握以上知识是解题的关键.
18．（1）点E（3，4），过点E的反比例函数的解析式；（2）点D坐标（，）
【分析】（1）由矩形的性质可得两对边分别相等，利用翻折的性质可得OD＝OA＝BC=8，∠AOB＝∠BOD，等量代换和等角对等边的性质可得OE＝BE，设CE＝x，则BE＝OE＝8－x，利用勾股定理可得x的值，继而求得点E坐标，继而设反比例函数解析式，代入即可求解；
（2）过点D作DF⊥BC，可得△COE∽△FDE，利用三角形等积法求得，利用勾股定理求出，继而即可求解．
【详解】（1）∵长方形OABC中，OA=8，OC=4，∠AOB＝∠CBO
∴BC＝OA＝8，AB＝OC＝4，
由折叠的性质可得：OD＝OA＝BC=8，∠AOB＝∠BOD
∴∠CBO＝∠BOD
∴OE＝BE
设CE＝x，则BE＝OE＝8－x，
在Rt△COE中，由勾股定理可得：即
解得：
∴点E（3，4）
设过点E的反比例函数的解析式
将点E（3，4）代入上式可得：
∴
故过点E的反比例函数的解析式
（2）由（1）知，CE＝3，OE＝BE＝8－CE＝5，DE＝8－OE＝3，
过点D作DF⊥BC，
由翻折的性质可得∠BAO＝∠BDE＝90°
∴
解得：，
∵在Rt△DEF中，，
∴，
∴，
∴点D坐标（，）
【点睛】本题考查矩形的性质、翻折的性质、勾股定理、反比例函数解析式、等积法，解题的关键是学会做辅助线，求出关键线段的长．
19．
【分析】过点P作PD⊥x轴于点D，由等边三角形的性质可知OD=OQ=1，再根据勾股定理求出PD的长，故可得出P点坐标，再利用待定系数法求解即可．
【详解】解：过点P作PD⊥x轴于点D，
∵△OPQ是边长为2的等边三角形，
∴OD=OQ=×2=1，
在Rt△OPD中，
∵OP=2，OD=1，
∴PD=，
∴P（1，），
设反比例函数为：y=（k≠0），因为反比例函数的图象过点P，所以k=．
所以所求解析式为：y=．
【点睛】本题考查的是用待定系数法求反比例函数的解析式，先根据题意得出点P的坐标是解答此题的关键．
20．(1)（0，2），（1，0），（m＋1，2）
(2)4；y＝-2x＋6
【分析】（1）根据OB＝2可得点B的坐标，根据OD＝1可得点D的坐标为（1，0），由平移规律可得点C的坐标；
（2）根据点C和D的坐标列方程可得m的值，从而得k的值，再利用待定系数法可得直线AC的解析式．
【详解】（1）∵点B在y轴上，，
∴B（0，2），
∵点D落在x轴正半轴上，且
∴D（1，0），
∴线段AB向下平移2个单位，再向右平移1个单位，得到线段CD，
∵点A（m，4），
∴C（m＋1，2），
故答案为：（0，2），（1，0），（m＋1，2）；
（2）∵点A和点C在反比例函数的图象上，
∴k＝4m＝2（m＋1），
∴m＝1，
∴A（1，4），C（2，2），
∴k＝1×4＝4，
设直线AC的表达式为：，
∴ 解得，
∴直线AC的表达式为：y＝-2x＋6．
【点睛】此题主要考查了一次函数和反比例函数的综合应用以及平移的性质，根据OB和OD的长得出平移的规律是解题关键．
21．(1)；
(2)；
(3)存在，点F的坐标为或或
【分析】（1）将和两点，代入函数，得到二元一次方程组，求解即可得到答案；
（2）先利用待定系数法求出直线的解析式为，过点作轴，交轴于点，交于点，设，则，，进而得到，，再根据，求出的值，得到点的坐标，设直线的解析式为，利用待定系数法，即可求出直线的解析式；
（3）由直线得解析式，求得，，根据等腰直角三角形的性质，分三种情况讨论：①当点为直角顶点时；②当点为直角顶点时；③当点为直角顶点时，分别构造全等三角形求解，即可求出点的坐标．
【详解】（1）解：函数的图象过和两点，
，解得：；
（2）解：由（1）可知，，
，
设直线的解析式为，
则，解得：，
直线的解析式为，
过点作轴，交轴于点，交于点，
设，则，，
则，，
，
，
，
解得：，（舍），
，
直线由直线沿x轴向左平移得到，
设直线的解析式为，
将代入，得，
解得：，
直线的解析式为；

（3）解：存在，点F的坐标为或或，理由如下：
直线交x轴于点D，交y轴于点E，
令，则；令，则，解得：，
，，
，，
是等腰直角三角形，
①当点为直角顶点时，此时，，
过点作轴于点，
，
，
，
，
在和中，
，
，
，，
，
点在第二象限，
；

②当点为直角顶点时，此时，，
过点作轴于点，
同①理可得，，
，，
，
点在第二象限，
；

③当点为直角顶点时，此时，，
过点作轴于点，轴于点，
，
，
，
，
在和中，
，
，
，，
又，
四边形是正方形，
，
，
，
，
点在第二象限，
；
综上可知，第二象限内存在点F，使得为等腰直角三角形，点F的坐标为或或．

【点睛】本题考查了待定系数法求反比例函数解析式和一次函数解析式，解二元一次方程组，等腰三角形的性质，全等三角形的判定和性质，正方的判定和性质等知识，作辅助线构造全等三角形是解题关键．
22．(1)；(2)见解析;（3）见解析.
【分析】（1）利用待定系数易得反比例函数解析式为；
（2）根据反比例函数的性质求解；
（3）根据反比例函数图象上点的坐标特征进行判断．
【详解】解：设反比例函数解析式为，
把代入得，
所以反比例函数解析式为；
因为，
所以这个函数的图象分布在第二、四象限，在每一象限，随的增大而增大；当时，；当时，，
所以点，点在比例函数的图象上，点不在．
【点睛】本题考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.也考查了反比例函数的性质.
23．（1）；（2）满足条件的所有围建方案：AD=5m，DC=12m或AD=6m，DC=10m或AD=10m，DC=6m．
【详解】解：（1）如图，AD的长为，DC的长为，
根据题意，得，即．
∴与之间的函数关系式为．
（2）由，且都为正整数，
∴ｘ可取1，2，3，4，5，6，10，12，15，20，30，60．
∵
∴符合条件的有：时，；时，；时，．
答：满足条件的所有围建方案：AD=5m，DC=12m或AD=6m，DC=10m或AD=10m，DC=6m．
24．（1）m＞5；（2）m＝13．
【分析】（1）由反比例函数图象位于第一象限得到m﹣5大于0，即可求出m的范围；
（2）根据反比例函数系数k的几何意义得出（m﹣5）＝4，解得即可．
【详解】解：（1）∵这个反比例函数的图象分布在第一、第三象限，
∴m﹣5＞0，
解得m＞5；
（2）∵S△OAB＝|k|，△OAB的面积为4，
∴（m﹣5）＝4，
∴m＝13．
【点睛】此题考查了反比例函数系数k的几何意义，反比例函数的图象与性质，根据系数k的几何意义得出（m 5）＝4是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)