第五章二次函数同步练习（含解析）

中小学教育资源及组卷应用平台
第五章二次函数
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．二次函数的图象如图所示，下列说法错误的是（ ）
A．函数的最大值为4
B．函数图象关于直线对称
C．当时，y随x的增大而减小
D．x＝1或是方程的两个根
2．已知二次函数，当函数值y随x值的增大而增大时，x的取值范围是（ ）
A． B． C． D．
3．如图，抛物线与轴交于点，其对称轴为直线，结合图象分析下列结论：；；③当时，y随x的增大而增大；④一元二次方程的两根分别为， ；⑤若m， n为方程的两个根，则且，其中正确的结论有（ ）个．

A．2 B．3 C．4 D．5
4．如图，在同一直角坐标系中，，函数和的图象可能是（　　）
A． B．
C． D．
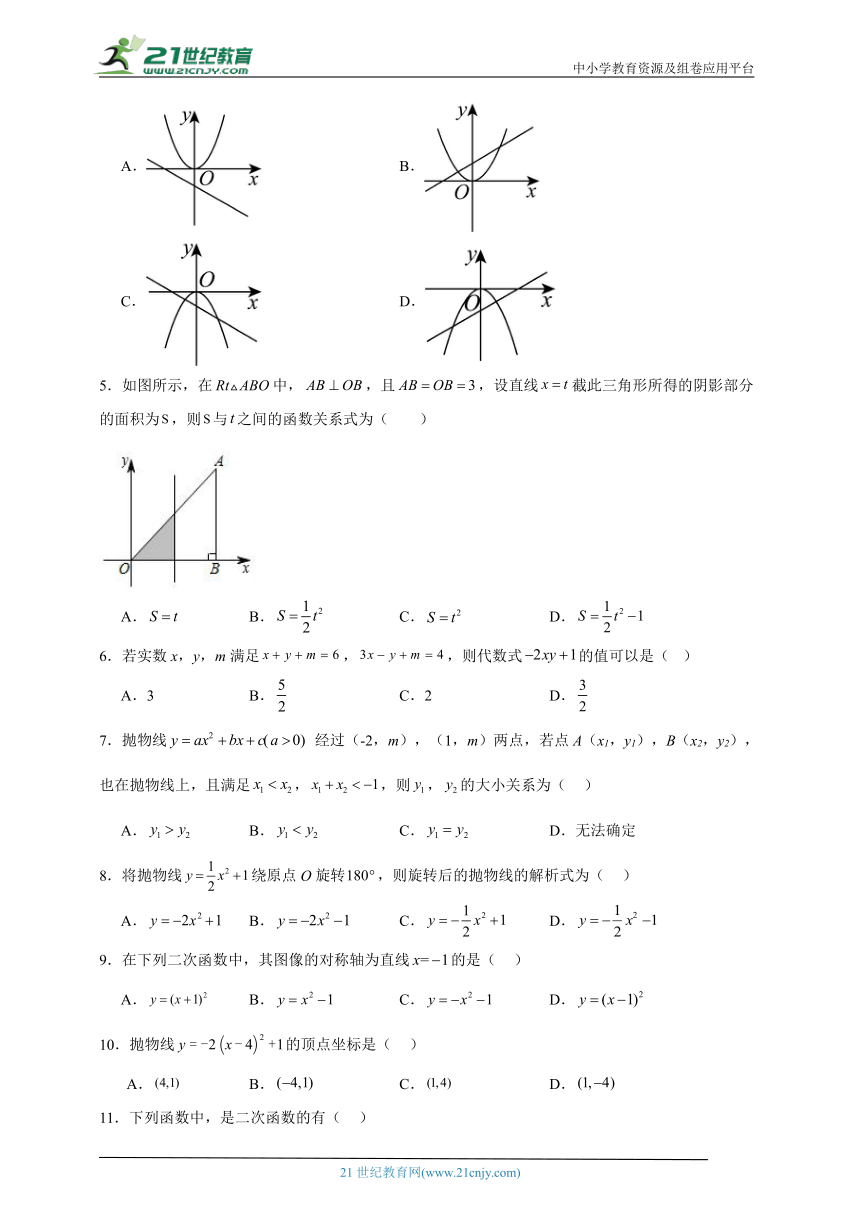
5．如图所示，在中，，且，设直线截此三角形所得的阴影部分的面积为，则与之间的函数关系式为（　　）
A． B． C． D．
6．若实数x，y，m满足，，则代数式的值可以是（ ）
A．3 B． C．2 D．
7．抛物线 经过（-2，m），（1，m）两点，若点A（x1，y1），B（x2，y2），也在抛物线上，且满足，，则，的大小关系为（ ）
A． B． C． D．无法确定
8．将抛物线绕原点O旋转，则旋转后的抛物线的解析式为（ ）
A． B． C． D．
9．在下列二次函数中，其图像的对称轴为直线的是（ ）
A． B． C． D．
10．抛物线的顶点坐标是（ ）
A． B． C． D．
11．下列函数中，是二次函数的有（ ）
①；②；③；④．
A．1个 B．2个 C．3个 D．4个
12．若实数x，y，m满足，，则代数式的值可以是（ ）
A．3 B． C．2 D．
二、填空题
13．已知二次函数的图象上两点，若，则 ．
14．抛物线关于轴对称的抛物线的解析式为 ．
15．抛物线的顶点坐标 ．
16．如图，二次函数与一次函数的图象相交于点，，则使成立的的取值范围是 ．
17．若为二次函数的图像上的三点，则的大小关系是 ．（用“<”连接）
三、解答题
18．如果抛物线的顶点在抛物线上，同时，抛物线的顶点在抛物线上，那么，我们称抛物线与关联．
(1)已知抛物线①：与②：，请判断抛物线①与抛物线②是否关联，并说明理由；
(2)将抛物线：沿x轴翻折，再向右平移m（m＞0）个单位，得到抛物线，若抛物线与关联，求m的值；
(3)点A为抛物线：y＝﹣2x2+4x+3的顶点，点B为抛物线关联的抛物线的顶点（点B位于x轴的下方），是否存在以AB为斜边的等腰直角三角形ABC，使其直角顶点C在x轴上？若存在，求出C点的坐标；若不存在，请说明理由．
19．观察二次函数的图象，并填空．
(1)图象与x轴的交点也是它的________，这个点的坐标是________；
(2)二次函数的图象是一条________，它的开口向________，它的对称轴为________；
(3)当时，随着x值的增大，y的值________；当时，随着x值的增大，y的值________．
20．已知函数是关于x的二次函数．
(1)求m的值；
(2)当m为何值时，该函数图像的开口向下？
(3)当m为何值时，该函数有最小值？
(4)试说明函数的增减性．
21．已知抛物线经过，，三点，求该抛物线的解析式．
22．已知抛物线的顶点为，与y轴交于点．
(1)求抛物线的解析式；
(2)点P为直线BC抛物线上的一动点，当△PBC面积最大时，求点P的坐标．
23．已知二次函数图象经过点和．求该二次函数的表达式及图象的顶点坐标．
24．某工厂一种产品2013年的产量是100万件，计划2015年产量达到121万件．假设2013年到2015年这种产品产量的年增长率相同．
(1)求2013年到2015年这种产品产量的年增长率；
(2)2014年这种产品的产量应达到多少万件？
《第五章二次函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C C B D A D A A
题号 11 12
答案 B D
1．C
【分析】根据二次函数的图象结合二次函数的性质即可得出、二次函数对称轴为以及二次函数的顶点坐标，再逐项分析四个选项即可得出结论．
【详解】解：观察二次函数图象，发现：
开口向下，，抛物线的顶点坐标为，对称轴为，与轴的一个交点为．
A、，
二次函数的最大值为顶点的纵坐标，即函数的最大值是4，选项正确，不符合题意；
B、二次函数的对称轴为，
函数的图象关于直线对称，选项正确，不符合题意；
C、当时，随的增大而增大，选项错误，符合题意；
D、二次函数的图象关于直线对称，且函数图象与轴有一个交点，
二次函数与轴的另一个交点为．
x＝1或是方程的两个根，选项正确，不符合题意．
故选：C．
【点睛】本题考查了二次函数的图象以及二次函数的性质，解题的关键是根据二次函数的性质逐条分析四个选项．本题属于基础题，难度不大，解决该题型题目时，结合函数图象以及二次函数的性质求解．
2．B
【分析】先将函数表达式写成顶点式，根据开口方向和对称轴即可判断．
【详解】解：∵
∵开口向上，对称轴为x=1，
∴x＞1时，函数值y随x的增大而增大．
故选：B．
【点睛】本题考查的是二次函数的图像与性质，比较简单，需要熟练掌握二次函数的图像与性质．
3．C
【分析】由开口方向确定a，由与y轴交点判c，由对称轴及a判b，结合对称轴及的点即可判a，c关系，根据交点即对称性即可判方程的根，即可得到答案；
【详解】解：由函数图象可得，
，，，
则，故①正确；
，得，
∵时，，
∴，
∴，
∴，故②正确；
由图象可知，当时，y随x的增大而增大，当时，y随x的增大而减小，故③错误；
∵抛物线与x轴交于点，其对称轴为直线，
∴该抛物线与x轴的另一个交点的坐标为，
∴的两个根为，，
∴的两个根为，，
∴一元二次方程的两根分别为， ，故④正确；
∵该函数与x轴的两个交点为，，
∴该函数的解析式可以为，
当时，，
∴当对应的x的值一个小于，一个大于2，
∴若m，为方程的两个根，则且，故⑤正确；
故选：C．
【点睛】本题考查根据二次函数图像判断各个式子的值，解题的关键是根据图像判断各项系数与0的关系，结合对称轴及与x轴交点确定方程的解．
4．C
【分析】根据一次函数、二次函数的图象与性质逐项判断即可求解．
【详解】解： A.∵抛物线开口向上，∴，∵直线从左至右下降，∴，∴k的取值矛盾，故原选项不符合题意；
B. 由直线解析式得直线与y轴交点为，与直线图象矛盾，故原选项不符合题意；
C.∵抛物线开口向下，∴，∵直线从左至右下降，∴，k的取值一致且直线与y轴交于负半轴，故原选项有可能正确，符合题意；
D. ∵抛物线开口向下，∴，∵直线从左至右上升，∴，∴k的取值矛盾，故原选项不符合题意．
故选：C
【点睛】本题考查了一次函数、二次函数的图象与性质，熟知两种函数的图象与性质是解题关键．
5．B
【分析】中，，且，可得；再由平行线的性质得出，即，进而证明，最后根据三角形的面积公式，求出与之间的函数关系式．
【详解】解：如图所示，
∵中，，且，
∴，
∵，
∴，
∴，
∴，
∴，
∴
，
即：．
故选：B．
【点睛】本题主要考查的是二次函数解析式的求法，考查了等腰直角三角形的性质，平行线的判定和性质，等腰三角形的判定，三角形的面积等知识点．解题的关键是能够找到题目中的有关面积的等量关系．
6．D
【详解】由题意可得解得
∴，∵，∴A，B，C不符合题意，D符合题意．
7．A
【分析】根据二次函数的对称轴求出a=b，计算即可判断；
【详解】解：∵抛物线经过（-2，m），（1，m），可知对称轴为：，即a=b，
，，
，
∵，∴，
∵，∴，
∵，∴，
∴，即，
故选： A．
【点睛】本题考查了二次函数的性质，利用对称性求出对称轴从而得出a，b关系是解题关键．
8．D
【分析】根据抛物线绕原点O旋转得到旋转后的抛物线与原抛物线关于原点对称，即可得到答案；
【详解】解：∵抛物线绕原点O旋转，
∴旋转后的抛物线与原抛物线关于原点对称，
∴旋转后的抛物线：，
即．
故选：D．
【点睛】本题考查旋转的性质，解题的关键是根据原点旋转得到关于原点对称．
9．A
【分析】根据二次函数顶点式的图像与性质直接求解即可得到答案．
【详解】解：A、的对称轴为；
B、的对称轴为；
C、的对称轴为；
D、的对称轴为；
故选：A．
【点睛】本题考查二次函数顶点式的图像与性质，熟记二次函数顶点式的图像与性质是解决问题的关键．
10．A
【分析】本题考查二次函数的图象和性质．根据顶点式的顶点坐标为求解即可．
【详解】解：抛物线的顶点坐标是．
故选：A．
11．B
【分析】根据二次函数的定义，即可求解．
【详解】解：①，是二次函数，符合题意；
②，不符合二次函数的定义，不是二次函数；
③，是二次函数，符合题意；
④，不符合二次函数的定义，不是二次函数；
故选：B．
【点睛】本题主要考查了二次函数的定义，熟练掌握形如：这样的函数是二次函数是解题的关键．
12．D
【详解】由题意可得解得
∴，∵，∴A，B，C不符合题意，D符合题意．
13．
【分析】根据抛物线的轴对称的性质即可求解．
【详解】解：∵抛物线的对称轴为：，两点在抛物线上，且，
，
解得，，
故答案为：-2．
【点睛】本题考查了二次函数的图像和性质，根据抛物线的轴对称的性质是解本题的关键．
14．
【分析】根据题意可知抛物线的顶点坐标为，进而可得该抛物线关于x轴对称的顶点坐标为，然后问题可求解．
【详解】解：由抛物线可知顶点坐标为，
∴该抛物线关于轴对称的抛物线的顶点坐标为，
∴抛物线关于轴对称的抛物线的解析式为；
故答案为．
【点睛】本题主要考查二次函数的性质及轴对称，熟练掌握二次函数的性质及轴对称是解题的关键．
15．
【分析】本题考查二次函数的图像和性质，把二次函数的解析式改成顶点式，即可求得顶点坐标．转化成顶点式是解题的关键．
【详解】∵，
∴抛物线的顶点坐标是．
故答案为：．
16．或
【分析】本题考查二次函数与不等式的关系，解题关键是结合图象求解．根据抛物线与直线交点坐标，结合图象求解．
【详解】解：抛物线与直线交点坐标为，，
或时，抛物线在直线上方，
使成立的的取值范围是或．
故答案为：或
17．
【分析】分别将代入解析式分别计算出的值，然后比较大小．
【详解】解：把代入得，
把代入得，
把代入得，
∴．
故答案为：
【点睛】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
18．(1)抛物线①与抛物线②关联，理由见解析
(2)m＝
(3)存在，点C的坐标为：（﹣2，0）或（﹣，0）或（4，0）或（，0）
【分析】（1）根据两抛物线的关联依次判断即可；
（2）根据两抛物线关联的定义直接列式得出结论；
（3）分当点C位于AD左侧和当点C位于AD右侧，借助关联的意义设出点C坐标，表示出点B坐标代入抛物线解析式即可求出点C坐标．
【详解】（1）解：由①知，，
∴抛物线①：的顶点坐标为（1，5），
把x＝1代入抛物线②：，得y＝5，
∴抛物线①的顶点在抛物线②上，
又由②，
∴抛物线②的顶点坐标为（﹣1，﹣3），
把x＝﹣1代入抛物线①中，得，y＝﹣3，
∴抛物线②的顶点在抛物线①上，
∴抛物线①与抛物线②关联．
（2）抛物线沿x轴翻折后抛物线为，
即：，
设平移后的抛物线解析式为，
把x＝1，y＝5代入得，
∴m＝±，
∵m＞0，
∴m＝，
（3）①当点C位于AD左侧时，过点A作AD⊥x轴于D，过点B作BE⊥x轴于E，如图1，
∴△ACD≌△CBE，
∴CE＝AD，BE＝CD
设C（c，0），
∵点B在x轴下方，
∴点B的纵坐标为c﹣1；
Ⅰ、当点C在x轴负半轴上时，即：c＜0，
∴B（c+5，c﹣1），
把B（c+5，c﹣1），代入中得，，
∴c＝﹣2或c＝﹣，
∴C（﹣2，0）或（﹣，0），
Ⅱ、当点C在x轴正半轴上时，即：0＜c＜1
把B（5+c，c﹣1），代入中得，，
∴c＝﹣2或c＝﹣（两个都不符合题意，舍去），
②当点C位于AD右侧时，
设C（c，0），同①的方法得出B（c﹣5，1﹣c），
将B（c﹣5，1﹣c）代入中得，，
∴c＝4或c＝，
∴C（4，0）或（，0），
即：点C的坐标为：（﹣2，0）或（﹣，0）或（4，0）或（，0）．
【点睛】此题是二次函数综合题，主要考查了新定义，全等三角形的判定和性质，解一元二次方程，分类讨论的思想，理解两抛物线关联是解本题的关键．
19．(1)顶点，
(2)抛物线，上，y轴（或直线）
(3)减小，增大
【分析】此题主要考查了二次函数的图象性质，掌握的性质是解题关键．
（1）根据的图象得出顶点位置及坐标；
（2）根据的图象得出其形状、开口方向及对称轴；
（3）根据的图象得出其性质．
【详解】（1）图象与x轴的交点也是它的顶点，这个点的坐标是．
故答案为：顶点，
（2）二次函数的图象是一条抛物线，它的开口向上，它的对称轴为y轴（或直线）．
故答案为：抛物线，上，y轴（或直线）
（3）当时，随着x值的增大，y的值减小；当时，随着x值的增大，y的值增大．
故答案为：减小，增大
20．(1)或
(2)当时，该函数图像的开口向下
(3)当时，原函数有最小值
(4)见解析
【分析】(1)由二次函数的定义可得故可求m的值．
(2)图像的开口向下，则，结合（1）中的结果，即可得m的值；
(3)函数有最小值，则，结合（1）中的结果，即可得m的值；；
(4)根据（1）中求得的m的值，先求出抛物线的解析式，函数的增减性由函数的开口方向及对称轴来确定．
【详解】（1）根据题意，得，
解得，
∴当或时，原函数为二次函数．
（2）∵图像开口向下，
∴，
∴，
∴，
∴当时，该函数图像的开口向下．
（3）∵函数有最小值，
∴，
则，
∴，
∴当时，原函数有最小值．
（4）当时，此函数为，开口向下，对称轴为y轴，
当时，y随x的增大而增大；当时，y随x的增大而减小；
当时，此函数为，开口向上，对称轴为y轴，
当时，y随x的增大而减小；当时，y随x的增大而增大．
【点睛】本题主要考查二次函数的性质，二次函数的最值，二次函数的增减性．二次函数的最值是顶点的纵坐标，当时，开口向上，顶点最低，此时纵坐标为最小值；当时，开口向下，顶点最高，此时纵坐标为最大值．考虑二次函数的增减性要考虑开口方向和对称轴两方面的因素，因此最好画图观察．
21．
【分析】根据抛物线经过，得出，再把，代入得到二元一次方程组，求解即可得到抛物线的完整解析式．
【详解】解：∵抛物线经过，
∴，
把，代入，得：，
解得：，
∴抛物线的解析式为：．
【点睛】本题考查了求二次函数解析式，根据抛物线经过的点代入求解参数是解题的关键．
22．(1)
(2)
【分析】（1）根据题意设函数顶点式，将点（2，-1），（0，3）代入，化成一般式即可；
（2）根据平行于y轴直线上两点间的距离是较大的纵坐标减较的纵坐标，可得DP的长，根据三角形的面积公式，可得二次函数，根据二次函数的性质，可得答案．
【详解】（1）解：设抛物线解析式为，
∵抛物线的顶点坐标为，
∴．
∵点在抛物线上，
∴．
解得．
∴抛物线的解析式为．
（2）解：如图，作PD垂直于x轴交BC于点D．
∵抛物线的解析式为，
∴点B的坐标为，则OB＝3．
∵点，
∴可求得直线BC的解析式为．
设，，则，．
，
整理得．
∵，
∴当时，有最大值，则P点坐标为．
【点睛】本题是二次函数综合运用，涉及到一次函数、图形的面积计算等，解（2）的关键是平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标得出DP的长．
23．，顶点坐标为
【分析】本题考查了二次函数的图象与性质，待定系数法求函数解析式，熟练掌握二次函数的性质是解答本题的关键．先用待定系数法求出函数解析式，再化为顶点式求解即可．
【详解】解：把点和代入，
得解得
∴二次函数的表达式为，
∵，
∴图象的顶点坐标为．
24．(1)这种产品产量的年增长率为
(2)2014年这种产品的产量应达到110万件
【分析】（1）通过增长率公式列出一元二次方程即可求出增长率；
（2）依据求得的增长率，代入2014年产量的表达式即可解决．
【详解】（1）解：设这种产品产量的年增长率为x，
根据题意列方程得，
解得，（舍去）．
答：这种产品产量的年增长率为．
（2）解：（万件）．
答：2014年这种产品的产量应达到110万件．
【点睛】本题主要考查了一元二次方程是实际应用——增长率问题，解题的关键是掌握：增长率问题中可以设基数为a，平均增长率为x，增长的次数为n，则增长后的结果为；而增长率为负数时，则降低后的结果为．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)