6.3相似图形同步练习(含解析)
图片预览



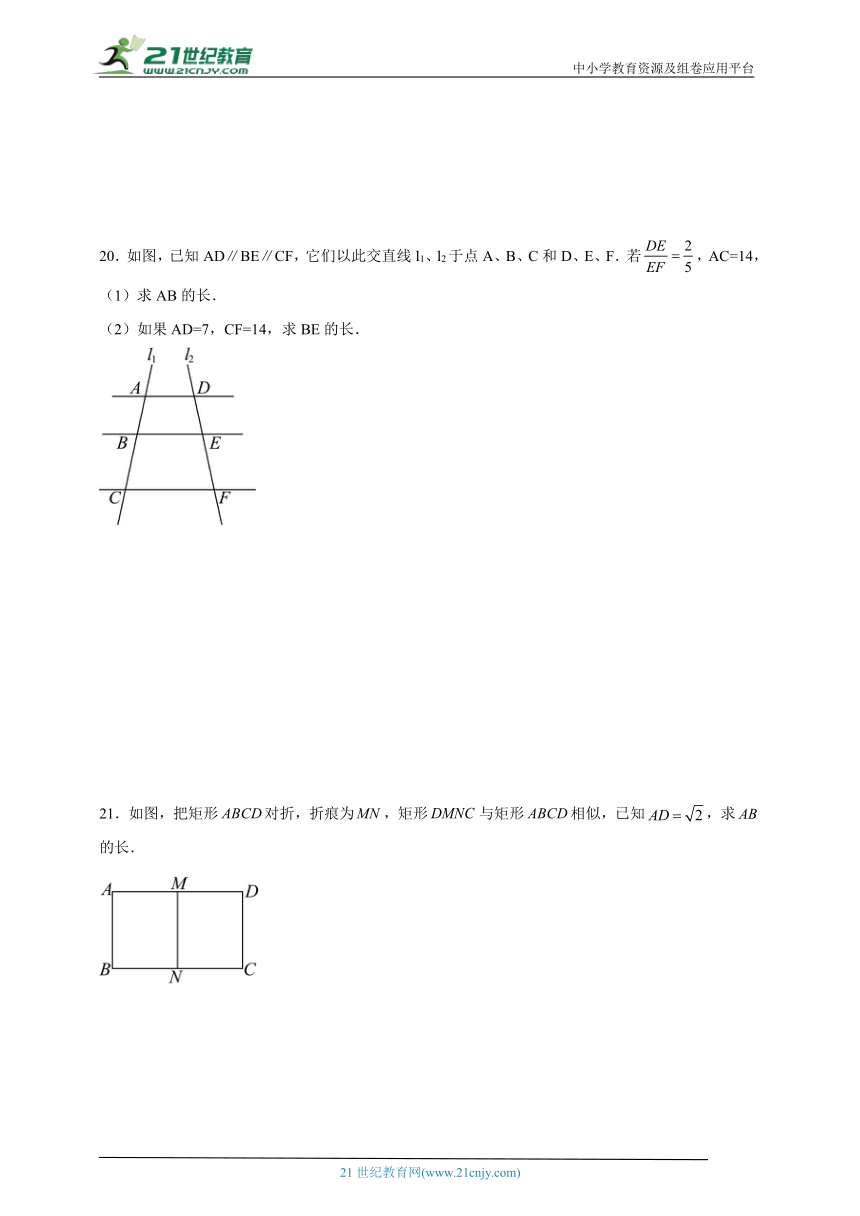
文档简介
中小学教育资源及组卷应用平台
6.3相似图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,用放大镜看到的多边形与原多边形相比较,不发生改变的是( )
A.周长 B.面积 C.每个内角的度数 D.每条边的长度
2.下列图形中一定相似的一组是( ).
A.邻边对应成比例的两个平行四边形 B.有一条边相等的两个矩形
C.有一条边相等的两个菱形 D.底角都是的两个等腰三角形
3.如图,过点的两直线将矩形分成甲、乙、丙、丁四个矩形,其中在上,且,下列对于矩形是否相似的判断,何者正确( )
A.甲、乙不相似 B.甲、丁不相似 C.丙、乙相似 D.丙、丁相似
4.“相似的图形”是( )
A.形状相同的图形 B.大小不相同的图形
C.能够重合的图形 D.大小相同的图形
5.彼此相似的矩形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
A.(2n﹣1,2n) B.(2n﹣,2n)
C.(2n﹣1﹣,2n﹣1) D.(2n﹣1﹣1,2n﹣1)
6.如图,梯形中,,、两点分别在、上.若,,,,且梯形与梯形相似,则与的长度比为何?( )
A.1:2 B.2:3 C.2:5 D.4:9
7.已知五边形五边形,相似比为.若五边形的周长为12,则五边形的周长为( )
A. B. C.12 D.27
8.如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则的值为( )
A. B. C. D.
9.如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( )
A.q<r,QE=RC B.q<r,QE<RC C.q=r,QE=RC D.q=r,QE<RC
10.下列两个图形一定是相似图形的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
11.下列各种图形相似的是 ( )
A.(1)、(2) B.(3)、(4) C.(1)、(3) D.(1)、(4)
12.下列说法正确的是( )
A.所有的等腰梯形都相似 B.所有的平行四边形都相似
C.所有的圆都相似 D.所有的等腰三角形都相似
二、填空题
13.两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积之和为130cm2,那么较小的多边形的面积是 cm2.
14.如图所示,长CD与C′D′之间距离为1,宽AD与A′D′之间距离为x,矩形ABCD的长AB=30,宽BC=20,x为 时,图中的两个矩形ABCD与A′B′C′D′相似.
15.一个10°的角在10倍的放大镜下看,度数是 ;一条10cm长的线段在10倍的放大镜下看,长度是 cm.
16.已知与相交于点O,若,,则的长为 .
17.如图是两个形状相同的举重图案,则的值是 .
三、解答题
18.在直角坐标系中描出下列各点:、、、,用线段依次联接点、、、、.
(1)你能得到什么图形?试说明理由.
(2)如果将上述四个点的横坐标不变,纵坐标均加上1,并且按同样的方式连接各点,你能得到一个什么图形?
(3)如果将上述四个点的纵坐标不变,横坐标均乘以,你能得到一个什么图形?
(4)上面三个图形中,哪些图形的形状相同?
19.如图所示,有一张矩形纸片ABCD,E、F分别是BC、AD上的点(不与顶点重合).如果直线EF将矩形分成面积相等的两部分,那么
(1)得到的两个四边形是否相似?若相似,请求出相似比;若不相似,请说明理由;
(2)这样的直线可以作多少条?
20.如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
21.如图,把矩形对折,折痕为,矩形与矩形相似,已知,求的长.
22.在如图所示的相似四边形中,求未知边x、y的长度和角度α的大小.
23.已知四边形与四边形相似,并且点A与点、点B与点、点C与点、点D与点分别对应.
(1)已知,,,求的度数;
(2)已知,,,,,求四边形的周长.
24.如图,已知AD∥EB∥FC,AC=12,DB=3,BF=7,求EC的长.
《6.3相似图形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A A A D A B D D
题号 11 12
答案 A C
1.C
【分析】本题考查了相似多边形的性质,熟记相关结论即可解答.
【详解】解:由题意得:用放大镜看到的多边形与原多边形是相似的关系,
用放大镜看到的多边形与原多边形相比较,周长、面积、每条边的长度的长度均增大了,
每个内角的度数保持不变,
故选:C.
2.D
【分析】利用相似多边形的判定,对应边成比例,对应角相等逐项判断即可.
【详解】解:A、邻边对应成比例的两个平行四边形,对应的角不一定相等,因而不一定相似,故错误,不符合题意;
B、有一条边相等的两个矩形,对应边的比不一定相等,因而不一定相似,故错误,不符合题意;;
C、有一个内角对应相等的两个平行四边形,对应边的比不一定相等,故错误,不符合题意;;
D、底角都是60°的等腰三角形一定是等边三角形,因而一定相似,故正确,符合题意;.
故选:D.
【点睛】本题考查了相似多边形的判定,解题关键是明确判定两个图形相似的依据是:对应边成比例,对应角相等.两个条件必须同时具备.
3.A
【分析】根据矩形的性质以及已知条件AP:PC=AD:AB=4:3,求得结果,采用排除法,得出正确答案.
【详解】如图,
∵AP:PC=AD:AB=4:3,AD∥BC,
∴,
∴甲与丁相似,故选项B错误,
∵当,
AM=EP,
∴甲与丙一定不相似,∴丙和丁不相似,故选项D错误,
∵,,DM=PF,
∴当,MP=AE,
∴甲与乙一定不相似,故选项A正确,
无法确定丙、乙是否相似,故选项C错误,
故选A.
【点睛】本题考查的是相似形的识别,关键要联系图形,根据相似图形的定义得出.
4.A
【分析】根据相似形的定义直接进行判断即可.
【详解】相似图形是形状相同的图形,大小可以相同,也可以不同,
故选A.
【点睛】本题考查了相似图形的定义,解题的关键是了解相似图形是形状相同的图形.
5.A
【分析】根据矩形的性质求出点的坐标,然后利用待定系数法求一次函数解析式求出,从而得到一次函数解析式,再根据一次函数图像上点的坐标特征求出的坐标,然后求出的坐标,...,最后根据点的坐标特征的变化规律写出的坐标即可.
【详解】,
相似矩形的长是宽的倍,
点的坐标分别为,
,
点在直线上,
,
解得,
,
点在直线上,
,
点的坐标为,
点的横坐标为,
点,
…,
的坐标为.
故选:.
【点睛】本题考查了相似多边形的性质,一次函数图象上点的坐标特征,根据点的系列坐标判断出相应矩形的长,再求出宽,然后得到点的系列坐标的变化规律是解题的关键.
6.D
【分析】根据两个梯形相似,则对应边的比成比例,即可求解.
【详解】解:∵梯形AEFD∽梯形EBCF,且DF:FC=2:3,
∴AD:EF=EF:BC=2:3,
∴AD=EF,BC=EF,
∴AD:EF:BC=:1:=4:6:9,
∴AD:BC=4:9.
故选D.
【点睛】本题主要考查了相似多边形的性质,正确理解性质是关键.
7.A
【分析】本题考查了相似多边形的性质,根据相似多边形周长的比等于相似比即可求解.
【详解】解:五边形五边形,相似比为,
五边形的周长于五边形的周长比为,
五边形的周长为12,
五边形的周长为.
故选:A.
8.B
【分析】根据相似多边形的性质进行求解即可.
【详解】解:
图形中正方形A1B1C1D1和正方形ABCD一定相似,OF,OF1分别是两个正方形的边心距, △OC1F 是等腰直角三角形, 因而OF: OC1=因而则的值为 .
故选B.
【点睛】本题主要考查相似多边形的性质,边数相同的正多边形一定相似, 边心距的比, 半径的比都等于相似比.
9.D
【详解】∵在矩形ABCD中,AB∥CD,
∵AP:PD=4:1,AQ:QE=4:1,
∴ ,
∴PQ∥CD,
∴ =4,
∵平行线间的距离相等,
∴q=r,
∵ =4,
∴ =,
∵AE<AC,
∴QE<CR.
故选D.
【点评】本题考查了平行线分线段成比例定理,矩形的性质,熟练掌握平行线分线段成比例定理是解题的关键.
10.D
【分析】根据相似图形的对应边成比例、对应角相等,逐项判断即可得出正确答案.
【详解】解:A、两个平行四边形的对应角不一定相等,对应边也不一定成比例,不一定相似,故此选项不符合题意;
B、两个矩形的对应角相等,但对应边的比不一定相等,不一定是相似图形,故此选项不符合题意;
C、两个菱形的对应边的比相等,但对应角不一定相等,不一定是相似图形,故此选项不符合题意;
D、两正方形一定相似,故此选项符合题意;
故选D.
【点睛】本题考查相似图形的识别,解题的关键是掌握相似图形的定义.对应角相等、对应边成比例的两个图形叫相似图形.
11.A
【详解】本题考查的是相似形的识别.
根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,对选项一一分析,选出正确答案.
解:(1)二者形状相同,大小不同,图形相似,故正确;
(2)二者形状相同,大小不同,图形相似,故正确;
(3)二者形状大小不同,图形不相似,故错误;
(4)二者形状大小不同,图形不相似,故错误.
(1)(2)正确;
故选A.
12.C
【详解】A选项中,因为“两个等腰梯形不一定相似”,所以A中说法错误;
B选项中,因为“两个平行四边形不一定相似”,所以B中说法错误;
C选项中,因为“所有的圆都是相似的”,所以C中说法正确;
D选项中,因为“两个等腰三角形不一定相似”,所以D中说法错误;
故选C.
点睛:根据相似多边形的定义:“对应边都成比例,对应角都相等的两个多边形相似”结合等腰梯形、平行四边形、圆和等腰三角形的特征分析即可得到正确结论.
13.40
【详解】试题分析:利用相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方可得.
解:两个相似多边形的一组对应边分别为3cm和4.5cm,
则相似比是3:4.5=2:3,
面积的比等于相似比的平方,即面积的比是4:9,
因而可以设较小的多边形的面积是4x(cm2),
则较大的是9x(cm2),
根据面积的和是130(cm2),
得到4x+9x=130,
解得:x=10,
则较小的多边形的面积是40cm2.
故答案为40.
14.1.5或9
【分析】根据相似多边形的性质列出比例式,代入计算得到答案.
【详解】解:当时,图中的两个矩形ABCD与A'B'C'D'相似,
解得,x=1.5,
当时,图中的两个矩形ABCD与A'B'C'D'相似,
解得,x=9,
故答案为:1.5或9.
【点睛】本题考查的是相似多边形的性质,掌握相似多边形的对应边成比例是解题的关键.
15. 10° 100
【详解】放大镜只改变图形的大小,不改变图形的形状,所以放大镜下角的度数不变,线段的长度会变化,故答案为(1).10°;(2).100.
16.6
【分析】根据平行列出比例式,代入数值求解即可.
【详解】解:∵,
∴,
即,
解得.
【点睛】本题考查了平行线分线段成比例定理,解题关键是列出比例式,准确进行计算.
17.
【分析】本题考查了相似多边形的性质,如果两个多边形相似,那么它们对应边的比相等,对应角相等,对应周长的比都等于相似比;它们对应面积的比等于相似比的平方.
根据相似多边形的性质:对应线段的比等于相似比列式求解即可.
【详解】解:由题意得,,
,
故答案为:.
18.(1)平行四边形,理由见解析;(2)得到一个一样大小的平行四边形,图形向上平移了1个单位;(3)得到一个平行四边形,与原图形关于轴对称;(4)上面三个图形形状均相同.
【分析】(1)根据题意做出图形进行判断即可;
(2)根据题意改变坐标,连接各点后进行判断;
(3)根据题意改变坐标,连接各点后进行判断;
(4)根据相似图形的定义进行判断.
【详解】(1)平行四边形.理由:
如图所示,
∵点A、C纵坐标相同,
∴AC∥x轴,
同理可知BD∥x轴,
∴AC∥BD,
又∵AC=BD=2
∴四边形ADBC是平行四边形.
(2)将上述四个点的横坐标不变,纵坐标均加上1,得到A1(2,4),B1(-2,0),C1(4,4),D1(-4,0),连接后如图所示,
得到一个一样大小的平行四边形,图形向上平移了1个单位.
(3)将上述四个点的纵坐标不变,横坐标均乘以,得到A2(-2,3),B2(2,-1),C2(-4,3),D2(4,-1),连接后如图所示,
得到一个平行四边形,与原图形关于轴对称.
(4)上面三个图形形状均相同.
【点睛】本题考查网格作图,根据坐标变化找出对应点是解决本题的关键.
19.见解析
【详解】(1)相似.理由如下:
因为EF将矩形ABCD分成面积相等的两部分,所以可设AB=a,AD=b,BE=x.
于是有,
所以x+AF=b-x+b-AF,即AF=b-x.
又EC=b-x,所以AF=EC.
在矩形ABCD中,AB=CD,AD=BC,AD∥BC,
所以DF=BE,∠AFE=∠FEC,∠DFE=∠BEF,∠A=∠B=∠C=∠D=90°.
所以在四边形ABEF与四边形CDFE中,有
∠A=∠C=90°,∠B=∠D=90°,∠AFE=∠FEC,∠BEF=∠DFE,
,
所以四边形ABEF与四边形CDFE相似,相似比为1.
(2)这样的直线有无数条,只要过矩形对角线的交点且满足条件即可.
20.(1) 4 10 (2) 9
【详解】【详解】(1)根据三条平行线截两条直线,所得的对应线段成比例可得,从而可得,再由AC=14即可求出AB的长;
(2)过点A作AG∥DF交BE于点H,交CF于点G,运用比例关系求出BH及HE的长,然后即可得出BE的长.
【详解】(1)∵AD∥BE∥CF,
∴,
∴,
∵AC=14,
∴AB=4,
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴,
∴BH=2,
∴BE=2+7=9.
【点睛】本题考查平行线分线段成比例的知识,解题的关键是掌握三条平行线截两条直线,所得的对应线段成比例.
21.
【分析】本题考查矩形的折叠问题,相似多边形的性质,根据相似多边形的性质列出比例式是解题的关键.
先根据的值可求出的长,再根据矩形与矩形相似得出矩形对应边的比例式,求出的长即可.
【详解】解:∵,
∴,
∵矩形与矩形相似,
∴,
即,
∴.
22.x=31.5;y=27;a=83°.
【分析】根据相似多边形的性质:对应角相等,对应边成比例.
【详解】由于两个四边形相似,它们的对应边成比例,对应角相等,
所以==,解得x=31.5,y=27.
a=360°﹣(77°+83°+117°)=83°.
【点睛】本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方.
23.(1)
(2)
【分析】(1)根据多边形相似的性质:对应角相等,求解即可;
(2)根据多边形相似的性质:对应边成比例,进行求解即可.
【详解】(1)解:∵四边形与四边形相似,
∴,
∴;
(2)解:∵四边形与四边形相似,
∴,
∴,
∴,,
∴四边形的周长
【点睛】本题主要考查了相似多边形的性质,熟练掌握其性质是解题的关键.
24.EC的长为.
【分析】根据AD∥EB∥FC,由平行线分线段成比例可得EC:AC= BF:DF,代入数据计算即可.
【详解】∵AD∥EB∥FC,
∴EC:AC= BF:DF,
∴EC:12=7:10,
∴EC=.
【点睛】本题考查了平行线分线段成比例定理,根据平行线写出对应比例式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.3相似图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,用放大镜看到的多边形与原多边形相比较,不发生改变的是( )
A.周长 B.面积 C.每个内角的度数 D.每条边的长度
2.下列图形中一定相似的一组是( ).
A.邻边对应成比例的两个平行四边形 B.有一条边相等的两个矩形
C.有一条边相等的两个菱形 D.底角都是的两个等腰三角形
3.如图,过点的两直线将矩形分成甲、乙、丙、丁四个矩形,其中在上,且,下列对于矩形是否相似的判断,何者正确( )
A.甲、乙不相似 B.甲、丁不相似 C.丙、乙相似 D.丙、丁相似
4.“相似的图形”是( )
A.形状相同的图形 B.大小不相同的图形
C.能够重合的图形 D.大小相同的图形
5.彼此相似的矩形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
A.(2n﹣1,2n) B.(2n﹣,2n)
C.(2n﹣1﹣,2n﹣1) D.(2n﹣1﹣1,2n﹣1)
6.如图,梯形中,,、两点分别在、上.若,,,,且梯形与梯形相似,则与的长度比为何?( )
A.1:2 B.2:3 C.2:5 D.4:9
7.已知五边形五边形,相似比为.若五边形的周长为12,则五边形的周长为( )
A. B. C.12 D.27
8.如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则的值为( )
A. B. C. D.
9.如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( )
A.q<r,QE=RC B.q<r,QE<RC C.q=r,QE=RC D.q=r,QE<RC
10.下列两个图形一定是相似图形的是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
11.下列各种图形相似的是 ( )
A.(1)、(2) B.(3)、(4) C.(1)、(3) D.(1)、(4)
12.下列说法正确的是( )
A.所有的等腰梯形都相似 B.所有的平行四边形都相似
C.所有的圆都相似 D.所有的等腰三角形都相似
二、填空题
13.两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积之和为130cm2,那么较小的多边形的面积是 cm2.
14.如图所示,长CD与C′D′之间距离为1,宽AD与A′D′之间距离为x,矩形ABCD的长AB=30,宽BC=20,x为 时,图中的两个矩形ABCD与A′B′C′D′相似.
15.一个10°的角在10倍的放大镜下看,度数是 ;一条10cm长的线段在10倍的放大镜下看,长度是 cm.
16.已知与相交于点O,若,,则的长为 .
17.如图是两个形状相同的举重图案,则的值是 .
三、解答题
18.在直角坐标系中描出下列各点:、、、,用线段依次联接点、、、、.
(1)你能得到什么图形?试说明理由.
(2)如果将上述四个点的横坐标不变,纵坐标均加上1,并且按同样的方式连接各点,你能得到一个什么图形?
(3)如果将上述四个点的纵坐标不变,横坐标均乘以,你能得到一个什么图形?
(4)上面三个图形中,哪些图形的形状相同?
19.如图所示,有一张矩形纸片ABCD,E、F分别是BC、AD上的点(不与顶点重合).如果直线EF将矩形分成面积相等的两部分,那么
(1)得到的两个四边形是否相似?若相似,请求出相似比;若不相似,请说明理由;
(2)这样的直线可以作多少条?
20.如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
21.如图,把矩形对折,折痕为,矩形与矩形相似,已知,求的长.
22.在如图所示的相似四边形中,求未知边x、y的长度和角度α的大小.
23.已知四边形与四边形相似,并且点A与点、点B与点、点C与点、点D与点分别对应.
(1)已知,,,求的度数;
(2)已知,,,,,求四边形的周长.
24.如图,已知AD∥EB∥FC,AC=12,DB=3,BF=7,求EC的长.
《6.3相似图形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A A A D A B D D
题号 11 12
答案 A C
1.C
【分析】本题考查了相似多边形的性质,熟记相关结论即可解答.
【详解】解:由题意得:用放大镜看到的多边形与原多边形是相似的关系,
用放大镜看到的多边形与原多边形相比较,周长、面积、每条边的长度的长度均增大了,
每个内角的度数保持不变,
故选:C.
2.D
【分析】利用相似多边形的判定,对应边成比例,对应角相等逐项判断即可.
【详解】解:A、邻边对应成比例的两个平行四边形,对应的角不一定相等,因而不一定相似,故错误,不符合题意;
B、有一条边相等的两个矩形,对应边的比不一定相等,因而不一定相似,故错误,不符合题意;;
C、有一个内角对应相等的两个平行四边形,对应边的比不一定相等,故错误,不符合题意;;
D、底角都是60°的等腰三角形一定是等边三角形,因而一定相似,故正确,符合题意;.
故选:D.
【点睛】本题考查了相似多边形的判定,解题关键是明确判定两个图形相似的依据是:对应边成比例,对应角相等.两个条件必须同时具备.
3.A
【分析】根据矩形的性质以及已知条件AP:PC=AD:AB=4:3,求得结果,采用排除法,得出正确答案.
【详解】如图,
∵AP:PC=AD:AB=4:3,AD∥BC,
∴,
∴甲与丁相似,故选项B错误,
∵当,
AM=EP,
∴甲与丙一定不相似,∴丙和丁不相似,故选项D错误,
∵,,DM=PF,
∴当,MP=AE,
∴甲与乙一定不相似,故选项A正确,
无法确定丙、乙是否相似,故选项C错误,
故选A.
【点睛】本题考查的是相似形的识别,关键要联系图形,根据相似图形的定义得出.
4.A
【分析】根据相似形的定义直接进行判断即可.
【详解】相似图形是形状相同的图形,大小可以相同,也可以不同,
故选A.
【点睛】本题考查了相似图形的定义,解题的关键是了解相似图形是形状相同的图形.
5.A
【分析】根据矩形的性质求出点的坐标,然后利用待定系数法求一次函数解析式求出,从而得到一次函数解析式,再根据一次函数图像上点的坐标特征求出的坐标,然后求出的坐标,...,最后根据点的坐标特征的变化规律写出的坐标即可.
【详解】,
相似矩形的长是宽的倍,
点的坐标分别为,
,
点在直线上,
,
解得,
,
点在直线上,
,
点的坐标为,
点的横坐标为,
点,
…,
的坐标为.
故选:.
【点睛】本题考查了相似多边形的性质,一次函数图象上点的坐标特征,根据点的系列坐标判断出相应矩形的长,再求出宽,然后得到点的系列坐标的变化规律是解题的关键.
6.D
【分析】根据两个梯形相似,则对应边的比成比例,即可求解.
【详解】解:∵梯形AEFD∽梯形EBCF,且DF:FC=2:3,
∴AD:EF=EF:BC=2:3,
∴AD=EF,BC=EF,
∴AD:EF:BC=:1:=4:6:9,
∴AD:BC=4:9.
故选D.
【点睛】本题主要考查了相似多边形的性质,正确理解性质是关键.
7.A
【分析】本题考查了相似多边形的性质,根据相似多边形周长的比等于相似比即可求解.
【详解】解:五边形五边形,相似比为,
五边形的周长于五边形的周长比为,
五边形的周长为12,
五边形的周长为.
故选:A.
8.B
【分析】根据相似多边形的性质进行求解即可.
【详解】解:
图形中正方形A1B1C1D1和正方形ABCD一定相似,OF,OF1分别是两个正方形的边心距, △OC1F 是等腰直角三角形, 因而OF: OC1=因而则的值为 .
故选B.
【点睛】本题主要考查相似多边形的性质,边数相同的正多边形一定相似, 边心距的比, 半径的比都等于相似比.
9.D
【详解】∵在矩形ABCD中,AB∥CD,
∵AP:PD=4:1,AQ:QE=4:1,
∴ ,
∴PQ∥CD,
∴ =4,
∵平行线间的距离相等,
∴q=r,
∵ =4,
∴ =,
∵AE<AC,
∴QE<CR.
故选D.
【点评】本题考查了平行线分线段成比例定理,矩形的性质,熟练掌握平行线分线段成比例定理是解题的关键.
10.D
【分析】根据相似图形的对应边成比例、对应角相等,逐项判断即可得出正确答案.
【详解】解:A、两个平行四边形的对应角不一定相等,对应边也不一定成比例,不一定相似,故此选项不符合题意;
B、两个矩形的对应角相等,但对应边的比不一定相等,不一定是相似图形,故此选项不符合题意;
C、两个菱形的对应边的比相等,但对应角不一定相等,不一定是相似图形,故此选项不符合题意;
D、两正方形一定相似,故此选项符合题意;
故选D.
【点睛】本题考查相似图形的识别,解题的关键是掌握相似图形的定义.对应角相等、对应边成比例的两个图形叫相似图形.
11.A
【详解】本题考查的是相似形的识别.
根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,对选项一一分析,选出正确答案.
解:(1)二者形状相同,大小不同,图形相似,故正确;
(2)二者形状相同,大小不同,图形相似,故正确;
(3)二者形状大小不同,图形不相似,故错误;
(4)二者形状大小不同,图形不相似,故错误.
(1)(2)正确;
故选A.
12.C
【详解】A选项中,因为“两个等腰梯形不一定相似”,所以A中说法错误;
B选项中,因为“两个平行四边形不一定相似”,所以B中说法错误;
C选项中,因为“所有的圆都是相似的”,所以C中说法正确;
D选项中,因为“两个等腰三角形不一定相似”,所以D中说法错误;
故选C.
点睛:根据相似多边形的定义:“对应边都成比例,对应角都相等的两个多边形相似”结合等腰梯形、平行四边形、圆和等腰三角形的特征分析即可得到正确结论.
13.40
【详解】试题分析:利用相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方可得.
解:两个相似多边形的一组对应边分别为3cm和4.5cm,
则相似比是3:4.5=2:3,
面积的比等于相似比的平方,即面积的比是4:9,
因而可以设较小的多边形的面积是4x(cm2),
则较大的是9x(cm2),
根据面积的和是130(cm2),
得到4x+9x=130,
解得:x=10,
则较小的多边形的面积是40cm2.
故答案为40.
14.1.5或9
【分析】根据相似多边形的性质列出比例式,代入计算得到答案.
【详解】解:当时,图中的两个矩形ABCD与A'B'C'D'相似,
解得,x=1.5,
当时,图中的两个矩形ABCD与A'B'C'D'相似,
解得,x=9,
故答案为:1.5或9.
【点睛】本题考查的是相似多边形的性质,掌握相似多边形的对应边成比例是解题的关键.
15. 10° 100
【详解】放大镜只改变图形的大小,不改变图形的形状,所以放大镜下角的度数不变,线段的长度会变化,故答案为(1).10°;(2).100.
16.6
【分析】根据平行列出比例式,代入数值求解即可.
【详解】解:∵,
∴,
即,
解得.
【点睛】本题考查了平行线分线段成比例定理,解题关键是列出比例式,准确进行计算.
17.
【分析】本题考查了相似多边形的性质,如果两个多边形相似,那么它们对应边的比相等,对应角相等,对应周长的比都等于相似比;它们对应面积的比等于相似比的平方.
根据相似多边形的性质:对应线段的比等于相似比列式求解即可.
【详解】解:由题意得,,
,
故答案为:.
18.(1)平行四边形,理由见解析;(2)得到一个一样大小的平行四边形,图形向上平移了1个单位;(3)得到一个平行四边形,与原图形关于轴对称;(4)上面三个图形形状均相同.
【分析】(1)根据题意做出图形进行判断即可;
(2)根据题意改变坐标,连接各点后进行判断;
(3)根据题意改变坐标,连接各点后进行判断;
(4)根据相似图形的定义进行判断.
【详解】(1)平行四边形.理由:
如图所示,
∵点A、C纵坐标相同,
∴AC∥x轴,
同理可知BD∥x轴,
∴AC∥BD,
又∵AC=BD=2
∴四边形ADBC是平行四边形.
(2)将上述四个点的横坐标不变,纵坐标均加上1,得到A1(2,4),B1(-2,0),C1(4,4),D1(-4,0),连接后如图所示,
得到一个一样大小的平行四边形,图形向上平移了1个单位.
(3)将上述四个点的纵坐标不变,横坐标均乘以,得到A2(-2,3),B2(2,-1),C2(-4,3),D2(4,-1),连接后如图所示,
得到一个平行四边形,与原图形关于轴对称.
(4)上面三个图形形状均相同.
【点睛】本题考查网格作图,根据坐标变化找出对应点是解决本题的关键.
19.见解析
【详解】(1)相似.理由如下:
因为EF将矩形ABCD分成面积相等的两部分,所以可设AB=a,AD=b,BE=x.
于是有,
所以x+AF=b-x+b-AF,即AF=b-x.
又EC=b-x,所以AF=EC.
在矩形ABCD中,AB=CD,AD=BC,AD∥BC,
所以DF=BE,∠AFE=∠FEC,∠DFE=∠BEF,∠A=∠B=∠C=∠D=90°.
所以在四边形ABEF与四边形CDFE中,有
∠A=∠C=90°,∠B=∠D=90°,∠AFE=∠FEC,∠BEF=∠DFE,
,
所以四边形ABEF与四边形CDFE相似,相似比为1.
(2)这样的直线有无数条,只要过矩形对角线的交点且满足条件即可.
20.(1) 4 10 (2) 9
【详解】【详解】(1)根据三条平行线截两条直线,所得的对应线段成比例可得,从而可得,再由AC=14即可求出AB的长;
(2)过点A作AG∥DF交BE于点H,交CF于点G,运用比例关系求出BH及HE的长,然后即可得出BE的长.
【详解】(1)∵AD∥BE∥CF,
∴,
∴,
∵AC=14,
∴AB=4,
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴,
∴BH=2,
∴BE=2+7=9.
【点睛】本题考查平行线分线段成比例的知识,解题的关键是掌握三条平行线截两条直线,所得的对应线段成比例.
21.
【分析】本题考查矩形的折叠问题,相似多边形的性质,根据相似多边形的性质列出比例式是解题的关键.
先根据的值可求出的长,再根据矩形与矩形相似得出矩形对应边的比例式,求出的长即可.
【详解】解:∵,
∴,
∵矩形与矩形相似,
∴,
即,
∴.
22.x=31.5;y=27;a=83°.
【分析】根据相似多边形的性质:对应角相等,对应边成比例.
【详解】由于两个四边形相似,它们的对应边成比例,对应角相等,
所以==,解得x=31.5,y=27.
a=360°﹣(77°+83°+117°)=83°.
【点睛】本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方.
23.(1)
(2)
【分析】(1)根据多边形相似的性质:对应角相等,求解即可;
(2)根据多边形相似的性质:对应边成比例,进行求解即可.
【详解】(1)解:∵四边形与四边形相似,
∴,
∴;
(2)解:∵四边形与四边形相似,
∴,
∴,
∴,,
∴四边形的周长
【点睛】本题主要考查了相似多边形的性质,熟练掌握其性质是解题的关键.
24.EC的长为.
【分析】根据AD∥EB∥FC,由平行线分线段成比例可得EC:AC= BF:DF,代入数据计算即可.
【详解】∵AD∥EB∥FC,
∴EC:AC= BF:DF,
∴EC:12=7:10,
∴EC=.
【点睛】本题考查了平行线分线段成比例定理,根据平行线写出对应比例式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
