6.5相似三角形的性质同步练习(含解析)
文档属性
| 名称 | 6.5相似三角形的性质同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
6.5相似三角形的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列五幅图均是由边长为1的16个小正方形组成的正方形网格,网格中的三角形的顶点都在小正方形的顶点上,那么在下列左边四幅图中的三角形,与图中的△ABC相似的是( )
A. B. C. D.
2.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是( )
A. B. C. D.
3.如图,直角三角形中,,于,于,则下列说法中正确的有( )个.
①图中有4个三角形与相似;②;③;④;⑤若,,则;⑥.
A.2个 B.3个 C.4个 D.5个
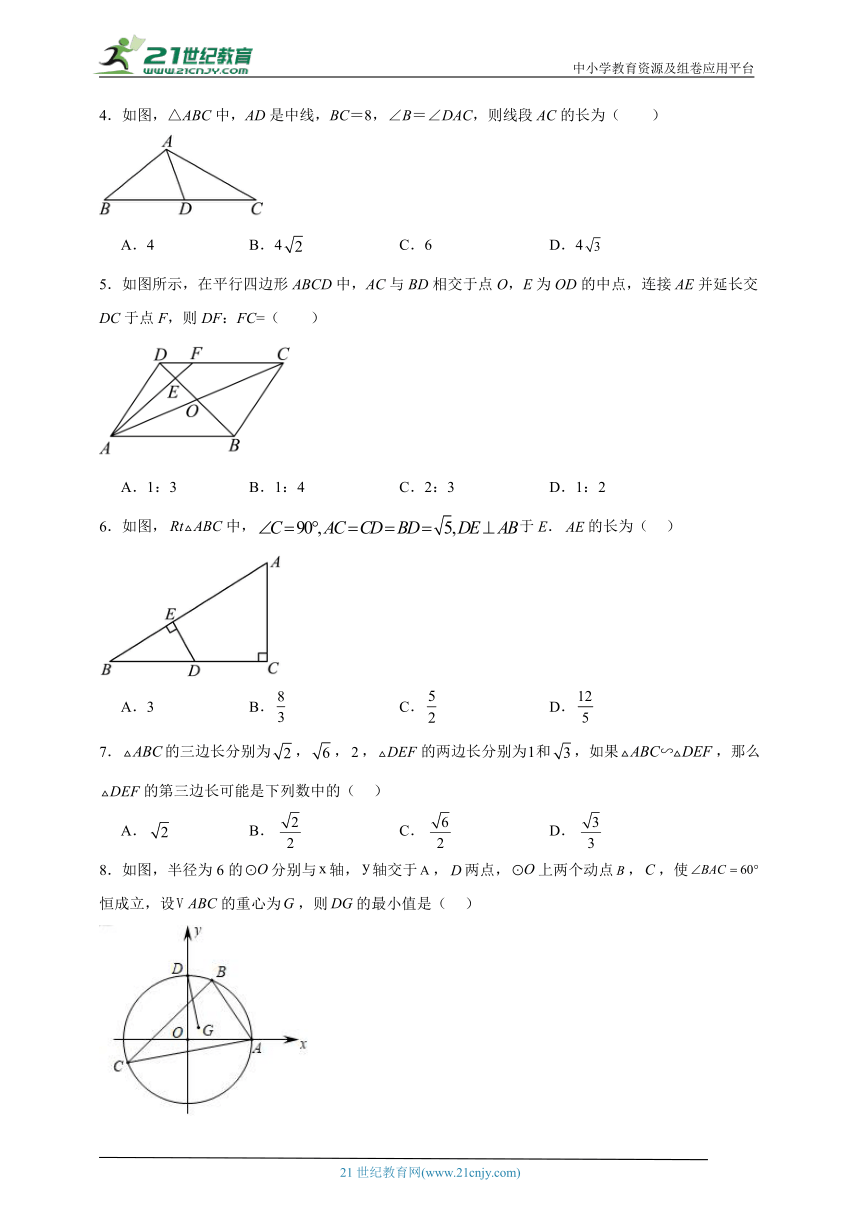
4.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
5.如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
A.1:3 B.1:4 C.2:3 D.1:2
6.如图,中,于E.的长为( )
A.3 B. C. D.
7.的三边长分别为,,,的两边长分别为和,如果,那么的第三边长可能是下列数中的( )
A. B. C. D.
8.如图,半径为6的分别与轴,轴交于,两点,上两个动点,,使恒成立,设的重心为,则的最小值是( )
A. B. C. D.
9.和三角形三个顶点相连后,一定能把三角形分成面积相等的三部分的是该三角形的
A.内心 B.外心 C.重心 D.垂心
10.如图,在矩形ABCD中,点E是对角线上一点,连接AE并延长交CD于点F,过点E作EG⊥AE交BC于点G,若AB=8,AD=6,BG=2,则AE=( )
A. B. C. D.
11.如图,已知,点D是边中点,且.若( )
A.3 B.4
C. D.
12.如图,已知DE∥BC,CD和BE相交于点O,S△DOE∶S△COB=9∶16,则DE∶BC为( )
A.2∶3 B.3∶4 C.9∶16 D.1∶2
二、填空题
13.如图,点A、B分别在平面直角坐标系xOy的y轴正半轴、x轴正半轴上,且OA=4,OB=3,将△AOB沿AB折叠,O的落点为P,若双曲线y=过点P,则k= .
14.如图,已知矩形对角线和相交于点O,点E是边上一动点,与相交于点F,连结.
(1)若点E为的中点,则= ;
(2)若点F为的中点,则= .
15.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径弦于),设,,他用含的式子表示图中的弦的长度,通过比较运动的弦和与之垂直的直径的大小关系,发现了一个关于正数的不等式,你也能发现这个不等式吗?写出你发现的不等式 .
16.如图,AB是的直径,AD是的切线,点C在上,,,,则BC的长为 .
17.中,,,,,是直线,上的点.若由,,构成的三角形与相似,,则的长为 .
三、解答题
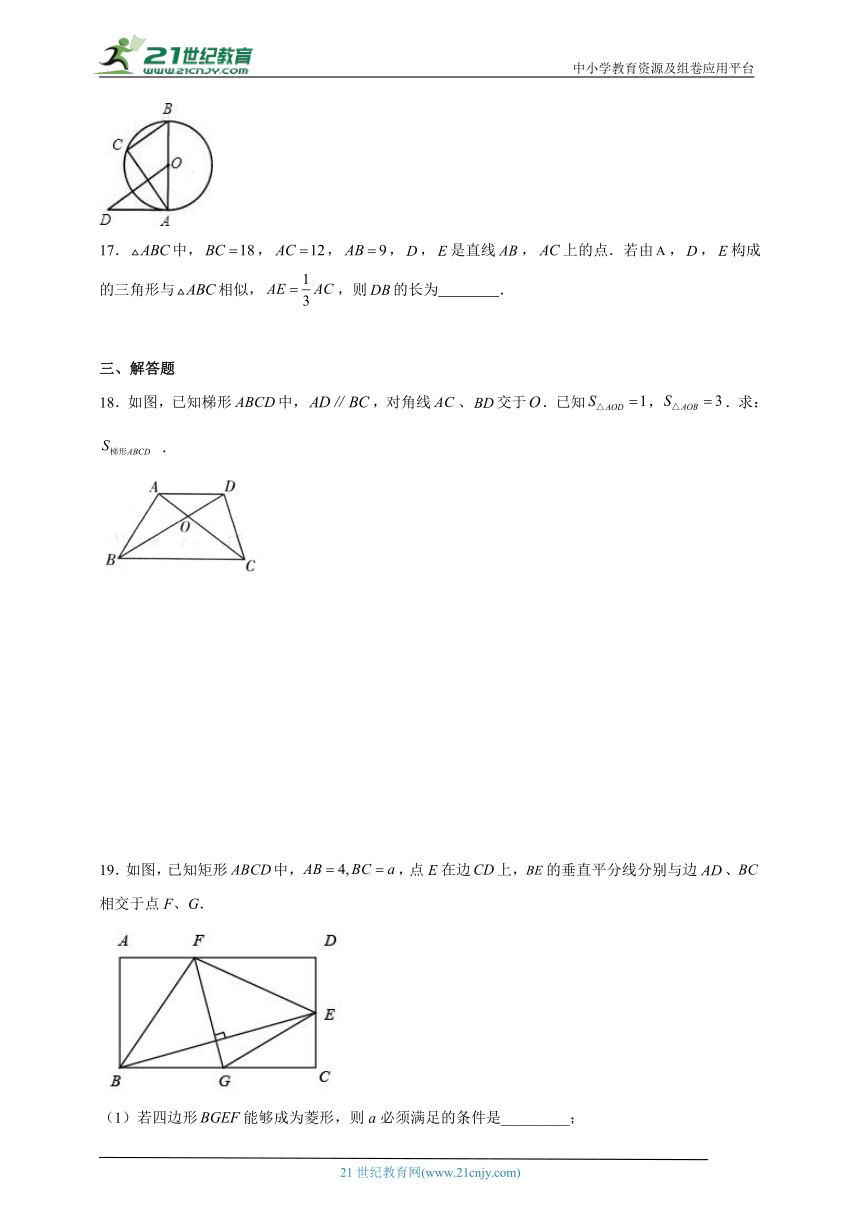
18.如图,已知梯形中,,对角线、交于.已知,.求: .
19.如图,已知矩形中,,点E在边上,的垂直平分线分别与边、相交于点F、G.
(1)若四边形能够成为菱形,则a必须满足的条件是_________;
(2)若,求的最小值;
(3)若经过点D、E、F的圆能够与直线、同时相切,求a的值.
20.已知:如图所示,在正方形ABCD中,F为DC的中点,E为BC上一点,且.求证:.
21.如图,AB与CD相交于点O,△OBD∽△OAC,=,OB=4,S△AOC=36,求
(1)AO的长.
(2)求S△BOD.
22.定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上动点,且AD=BE=CF.
求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=,求CF和AD的长.
23.已知等腰三角形ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F,
求证 :BE2=EF·EG.
24.如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
《6.5相似三角形的性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D B D A A B C B
题号 11 12
答案 D B
1.C
【分析】可利用正方形的边把对应的线段表示出来,利用三边对应成比例两个三角形相似,分别计算各边的长度即可解题.
【详解】解:根据勾股定理,,,
所以,夹直角的两边的比为,
观各选项,只有C选项三角形符合,与所给图形的三角形相似.
故选:C.
【点睛】此题考查了勾股定理在直角三角形中的运用,三角形对应边比值相等判定三角形相似的方法,本题中根据勾股定理计算三角形的三边长是解题的关键.
2.B
【详解】解:∵EF是点B、D的对称轴,
∴△BFE≌△DFE,
∴DE=BE.
∵在△BDE中,DE=BE,∠DBE=45°,
∴∠BDE=∠DBE=45°,
∴∠DEB=90°,
∴DE⊥BC.
在等腰梯形ABCD中,
∵=,
∴设AD=1,BC=4,过A作AG⊥BC于G,
∴四边形AGED是矩形,
∴GE=AD=1,
∵Rt△ABG≌Rt△DCE,
∴BG=EC=1.5,
∴AG=DE=BE=2.5,
∴AB=CD==,
∵∠ABC=∠C=∠FDE,∠CDE+∠C=90°,
∴∠FDE+∠CDE=90°,
∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°,
∴∠BDC=∠DFE,
∵∠DEF=∠DBC=45°,
∴△BDC∽△DEF,
∴,
∴DF=,
∴BF=,
∴AF=AB﹣BF=,
∴=.
故选B.
3.D
【分析】根据题意,对选项逐一分析,即可得出结论.
【详解】解:因为,,所以 =90°,=90°,所以=90°,可得,所以,所以,即,故选项②正确;
由题意,于,于E,所以=90°,,,,由相似的判定可知图中有4个三角形与相似,分别是、、、,故选项①正确;
因为,所以∠A与∠B互余,于,于,∠BCD与∠B互余,∠CDE与∠DCE互余,∠DCE与∠BCD互余,所以,故选项③正确;
因为,于,于,根据③中结论,所以,,因为,所以,两式相乘即可得,故选项④正确;
若,,由勾股定理可得AB=5,利用等面积可得,故选项⑤错误;
因为DE∥BC,所以,故选项⑥正确;
5个正确,
故答案为:D .
【点睛】本题考查了相似三角形的判定和性质,勾股定理的应用,余角的性质,熟练掌握相似三角形的判定和性质是解题的关键.
4.B
【分析】根据题意判断出△CBA∽△CAD,从而利用相似三角形的性质求解即可.
【详解】解:∵BC=8,AD是中线,
∴CD=BD=4,
在△CBA和△CAD中,
∵∠B=∠DAC,∠C=∠C,
∴△CBA∽△CAD,
∴,
∴AC2=CD BC=4×8=32,
∴AC=4;
故选:B.
【点睛】本题考查相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题关键.
5.D
【详解】解:在平行四边形ABCD中,AB∥DC,
则△DFE∽△BAE,
∴DF:AB=DE:EB.
∵O为对角线的交点,
∴DO=BO.
又∵E为OD的中点,
∴DE=DB,
则DE:EB=1:3,
∴DF:AB=1:3.
∵DC=AB,
∴DF:DC=1:3,
∴DF:FC=1:2.
故选D.
6.A
【分析】先证明,找出BE=2 DE,再利用勾股定理求解即可.
【详解】解:由题意知:∠BED=∠C,∠B=∠B,
∴,
∴,
∵,
∴,
∴BE=2DE,
由勾股定理知:,
代入计算得:BE=2,
又,
∴AE=5-2=3,
故答案为:A
【点睛】此题考查三角形相似,涉及到勾股定理求解,难度一般.
7.A
【分析】本题可根据相似三角形的性质:相似三角形的对应边成比例,来求出△DEF的第三边的长.
【详解】解:设△DEF的第三边长为x,
∵△ABC∽△DEF,
且△ABC的三边长分别为,,,△DEF的其中的两边长分别为1和,
∴==,
∴x=,
即:△DEF的第三边长为;
故选A.
【点睛】此题考查了相似三角形的性质,相似三角形的对应角相等,对应边的比相等.
8.B
【分析】连接AG并延长,交BC于点F,由△ABC的重心为G,可知F为BC的中点,再由垂径定理可知OF⊥BC,从而可求得OF的长;在AO上取点E,使AE=AO,连接GE,可判定△AGE∽△AFO,由相似三角形的性质列出比例式,求得GE的长,进而可得点E的坐标,利用勾股定理求出DE的长,根据G在以E为圆心,为半径的圆上运动,可知DG的最小值为DE的长减去,计算即可.
【详解】解:连接并延长,交于点,
的重心为,
为的中点,
,
,
,
,
,
的重心为,
,
在上取点,使,连接,
,,
,
,
.
在以为圆心,2为半径的圆上运动,
,,
,
的最小值是,
故选B.
【点睛】本题考查了三角形的重心、30°角所对的直角边等于斜边的一边、相似三角形的判定与性质、勾股定理在计算中的应用及勾股定理等知识点,熟练掌握相关性质及定理是解题的关键.
9.C
【分析】通过重心的性质和相似三角形得到S△OBC= S△ABC,同理可得S△OCA= S△ABC,S△OAB= S△ABC,问题得解.
【详解】解:如图,点O是△ABC的重心,
作△OBC的高OG和△ABC的高AH,
∴OG∥AH,
∴△OGD∽△AHD,
∴,
∴S△OBC= S△ABC,
同理可得:S△OCA= S△ABC,S△OAB= S△ABC
∴S△OBC= S△OCA = S△OAB,
∴一定能把三角形分成面积相等的三部分的是该三角形的重心,
故选C.
【点睛】本题考查三角形重心的定义和相似三角形的判定和性质,利用数形结合的思想是解决问题的关键.
10.B
【分析】过点作的平行线,分别交于点,先根据矩形的性质与判定可得四边形和四边形都是矩形,设,则,再根据相似三角形的判定证出,根据相似三角形的性质可得,从而可得,然后根据相似三角形的判定证出,根据相似三角形的性质可得的值,最后在中,利用勾股定理即可得.
【详解】解:如图,过点作的平行线,分别交于点,
四边形是矩形,,
,
四边形是矩形,
,
同理可得:四边形是矩形,
,
设,则,
,
,
,即,
解得,
,,
,
,
,
,
,
在和中,,
,
,即,
解得或,
经检验,是所列分式方程的根,且符合题意;不是所列分式方程的根,舍去,
,
,
故选:B.
【点睛】本题考查了矩形的判定与性质、相似三角形的判定与性质等知识点,通过作辅助线,构造相似三角形是解题关键.
11.D
【分析】由点D是边中点,得,再证明,得到,代入数值即可得到答案.
【详解】解:∵点D是边中点,
∴,
∵,,
∴,
∴,
∴,
∴,
∴(负值舍去),
故选:D
【点睛】此题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定是解题的关键.
12.B
【分析】首先根据平行得出三角形相似,然后根据相似三角形的面积之比等于相似比的平方得出答案.
【详解】∵DE∥BC, ∴△DOE∽△COB, ∴, ∴DE:BC=3:4,
故选B.
【点睛】本题主要考查的是相似三角形的性质,属于基础题型.明确相似三角形的面积之比等于相似比的平方是解题的关键.
13.
【分析】设P(x,y),过P作PD⊥x轴于D,过A作AC⊥PD于C,由垂直定义得∠AOB=∠ODC=∠C=90°,进而得∠PAC+∠APC=90°,再由折叠的性质得PA=OA=4,PB=OB=3,∠APB=90°,从而得∠APC+∠BPD=90°,∠BPD=∠PAC,进而证明△ACP∽△PDB,由相似三角形的性质即可求得点P的横、纵坐标,即可求解.
【详解】解:如图,设P(x,y),过P作PD⊥x轴于D,过A作AC⊥PD于C,
∵PD⊥x轴,AC⊥PD,x轴⊥y轴,
∴∠AOB=∠ODC=∠C=90°,
∴∠PAC+∠APC=90°,
∵OA=4,OB=3,将△AOB沿AB折叠,O的落点为P,
∴PA=OA=4,PB=OB=3,∠APB=90°,
∴∠APC+∠BPD=90°,
∴∠BPD=∠PAC,
∴△ACP∽△PDB
∴,即,
解得:x=,y=,
∵双曲线y=过点P,
∴k=×=.
故答案为:
【点睛】本题考查了坐标与图形,轴对称性质,正方形的性质,相似三角形的判定及性质,熟练掌握相似三角形的判定及性质是解题的关键.
14. /0.5 2
【分析】(1)根据矩形的性质可得点O是的中点,再结合已知可得是的中位线,从而可得,,然后证明8字模型相似三角形可得,利用相似三角形的性质进行计算即可解答;
(2)过作交于点,利用平行线分线段成比例和三角形全等即可求解.
【详解】(1)解:∵为矩形对角线交点,
∴.
∵点为中点,
∴为的中位线,
∴,,
∵,
∴,
∴;
(2)如图,过作交于点,
∴,
∴点为中点.
∴为的中位线,
∴,
∵,
∴.
又∵,,
∴,
∴,
∴,
即.
故答案为(1);(2)2.
【点睛】本题考查了相似三角形的判定与性质,矩形的性质以及全等三角形的判定和性质等,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
15.
【详解】解:连接AC,BD,
∵∠CAE=∠BDE,∠AEC=∠DEB,
∴△ACE∽△DBE,
∴,
∵CD⊥AB,
∴CE=DE,CD=2CE,
∴CE2=AE BE,
∴CE=.
∵CD=2CE,
∴CD=2CE=2.
又AB=x+y,且AB≥CD,得x+y≥2.
故答案为:x+y≥2.
16.
【分析】试题分析:根据圆周角定理可得∠C=90°,根据切线的性质可得∠OAD=90°,根据平行线的性质可得∠B=∠DOA,即可证得△OAD∽△BCA,最后根据相似三角形的性质求解即可.
【详解】∵AB是⊙O的直径,AD是⊙O的切线
∴∠C=90°,∠OAD=90°
∵BC//OD
∴∠B=∠DOA
∴△OAD∽△BCA
∴
∵AB=2,OD=3
∴,解得
故答案为
【点睛】本题考核知识点:圆周角定理,切线的性质,平行线的性质,相似三角形的判定和性质. 相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中半径常见的知识点.
17.或或或
【分析】由中,,,,,可求得的长,又由,,构成的三角形与相似,根据相似三角形的对应边成比例,即可求得的长.
【详解】∵△ABC中,BC=18,AC=12,AB=9,,
∴AE=4,
∵由A,D,E构成的三角形与△ABC相似,
∴当△ADE∽△ABC时,AD:AB=AE:AC=1:3,
∴
则BD=AB AD=6;
当△ADE∽△ACB时,AD:AC=AE:AB,
∴
∴
∴DB的长为:6或
当△ADE∽△ABC时,AD:AB=AE:AC=1:3,
∴
则BD=AB+AD=12;
当△ADE∽△ACB时,AD:AC=AE:AB,
∴
∴
综上所述:DB的长为:或或或
故答案为或或或.
【点睛】考查相似三角形的性质,注意分类讨论思想在解题中的应用.
18.16
【分析】由,可得 由可证 可得,根据即可计算出梯形ABCD的面积.
【详解】解:∵,
∴
∵
∴
∴
∴
∵
∴
【点睛】本题考查了相似比例与面积的关系,掌握面积间的关系是解题的关键.
19.(1);(2);(3).
【分析】(1)根据菱形的性质,找到E必在点D处,只要,那么形成的四边形必为菱形,就可求出a的取值范围;
(2)根据E点的运动过程,得到AF逐渐减小,即可得到当E在D时,最小,此时四边形为菱形;
(3)添加辅助线,过中点H作∥交AD于M,交BC于N,由题中所给已知条件可知,HN、EH、FH都是该圆的直径,用含a的式子表示HN和EF,再利用得出a的值
【详解】(1)
∵矩形,
∴BG∥DF
若四边形为菱形,则BG∥EF,
∴E必在点D处.
又,只要,那么形成的四边形必为菱形.
即.
(2)由运动规律可知,当E由C到D运动过程中,AF逐渐减小,所以当E在D时,最小,此时四边形为菱形.
设,则
∴
,解得,
即.
(3)如图所示,过中点H作∥交AD于M,交BC于N,
∵
∴H为过D、E、F的圆的圆心,EF为直径
∵经过点D、E、F的圆能够与直线、同时相切
∴,HN是半径
∵F在中垂线上,则
∴,(同角的余角相等),
∴
∴,
∴
又∵∥
∴
∴
∴
又
∴
又,则
∴
解得:.
【点睛】本题考查了菱形的性质和判定、勾股定理、全等三角形、圆的切线和相似三角形等相关知识,综合性较强.
20.见解析.
【分析】根据F为DC的中点,可得CE:DF=CF:AD=1:2,所以Rt△CEF∽Rt△DFA,然后根据相似三角形对应角相等可证出∠EFC+∠DFA=90°,即.
【详解】证明:∵四边形ABCD是正方形,
∴∠C=∠D=90°,
∵F是CD中点,
∴DF=CF=CD=AD,
∵CE=BC=CD,
∴CE:DF=CF:AD=1:2,
∴Rt△CEF∽Rt△DFA,
∴∠FAD=∠EFC,
∵∠FAD+∠DFA=90°,
∴∠EFC+∠DFA=90°,
∴∠EFA=90°,
∴AF⊥EF;
【点睛】本题考查了正方形的性质、相似三角形的判定和性质,根据题意得出CE:DF=CF:AD是解题关键.
21.(1)6;(2)16.
【分析】(1)由三角形相似可知,据此可求解;
(2)相似三角形的面积比等于相似比的平方.
【详解】解:(1)∵△OBD∽△OAC,
∴,
∵OB=4,
∴OA=6.
(2)∵△OBD∽△OAC,
∴,
∵S△AOC=36,
∴S△OBD=16.
【点睛】本题考查了相似三角形的性质以及相似比.
22.(1)证明见解析(2)2
【分析】(1)只要证明△DAF≌△EBD≌△FCE,可得DE=EF=DF,推出△DEF是等边三角形,推出∠DEF=∠EDF=∠B=∠A=60°,推出△DEF∽△ABC.可得△DEF是△ABC的子三角形;
(2)如图2中,作EH⊥AB于H.首先证明△DEF是等腰直角三角形,由△DEH≌△DFA,推出AD=HE,由△BEH是等腰直角三角形,推出HE=×=1,推出AD=1,由△BDE∽△CEF,可得,由此即可求出CF.
【详解】(1)证明:如图1中,
∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵AD=BE=CF,
∴AF=BD=CE,
∴△DAF≌△EBD≌△FCE,
∴DE=EF=DF,
∴△DEF是等边三角形,
∴∠DEF=∠EDF=∠B=∠A=60°,
∴△DEF∽△ABC.
∴△DEF是△ABC的子三角形.
(2)如图2中,作EH⊥AB于H.
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵△DEF是△ABC的子三角形,
∴△DEF∽△ABC,
∴DE=DF,∠EDF=90°,
∴∠ADF+∠AFD=90°,∠ADF+∠EDH=90°,
∴∠EDH=∠AFD,
∵∠DHE=∠A=90°,
∴△DEH≌△DFA,
∴AD=HE,
∵△BEH是等腰直角三角形,
∴HE=×=1,
∴AD=1,
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE,
∵∠B=∠DEF=45°,
∴△BDE∽△CEF,
∴,
∴CF=2.
【点睛】考查相似三角形的性质和判定、全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题.
23.见解析
【分析】先连接CE,由于AB=AC,AD⊥BC,利用等腰三角形三线合一定理可得BE=CE,再利用等边对等角可知∠EBC=∠ECB,易证∠ABE=∠ACE,结合CG∥AB,利用平行线的性质,可证∠CGF=∠FCE,再加上一组公共角,可证△CEF∽△GEC,于是CE2=EF·EG,从而得到BE2=EF·EG.
【详解】如图所示,连接EC,
∵AB=AC,AD⊥BC,
∴AD是∠BAC的角平分线,
∴BE=CE,
∴∠EBC=∠ECB,
又∵∠ABC=∠ACB,
∴∠ABC-∠EBC=∠ACB-∠ECB,
即∠ABE=∠ACE,
又∵CG∥AB,
∴∠ABE=∠CGF,
∴∠CGF=∠FCE,
又∠FEC=∠CEG,
∴△CEF∽△GEC,
∴CE2=EF·EG,
又CE=BE,
∴BE2=EF·EG.
【点睛】此题主要考查相似三角形的判定与性质,解题的关键是利用等腰三角形得到角度与线相等,从而解出此题.
24.(1)(2)(3)
【分析】(1)已知了抛物线图象上A、B两点的坐标,将它们代入抛物线的解析式中,即可求得m、n的值.
(2)根据A、B的坐标,易求得AB的长;根据平移的性质知:四边形A A′B′B一定为平行四边形,若四边形A A′B′B为菱形,那么必须满足AB=BB′,由此可确定平移的距离,根据“左加右减”的平移规律即可求得平移后的抛物线解析式.
(3)易求得直线AB′的解析式,联立平移后的抛物线对称轴,可得到C点的坐标,进而可求出AB、BC、AC、B′C的长;在(2)题中已经证得AB=BB′,那么∠BAC=∠BB′C,即A、B′对应,若以点B′、C、D为顶点的三角形与△ABC相似,可分两种情况考虑:①∠B′CD=∠ABC,此时△B′CD∽△ABC,②∠B′DC=∠ABC,此时△B′DC∽△ABC;
根据上述两种不同的相似三角形所得不同的比例线段,即可求得不同的BD长,进而可求得D点的坐标.
【详解】解:(1)由于抛物线经过A (﹣2,4)和点B (1,0),则有:
,解得;
故m=﹣,n=4.
(2)由(1)得:y=﹣x2﹣x+4=﹣(x+1)2+;
由A (﹣2,4)、B (1,0),可得AB==5;
若四边形A A′B′B为菱形,则AB=BB′=5,即B′(6,0);
故抛物线需向右平移5个单位,即:
y=﹣(x+1﹣5)2+=﹣(x﹣4)2+.
(3)由(2)得:平移后抛物线的对称轴为:x=4;
∵A(﹣2,4),B′(6,0),
∴直线AB′:y=﹣x+3;
当x=4时,y=1,故C(4,1);
所以:AC=3,B′C=,BC=;
由(2)知:AB=BB′=5,即∠BAC=∠BB′C;
若以点B′、C、D为顶点的三角形与△ABC相似,则:
①∠B′CD=∠ABC,则△B′CD∽△ABC,可得:
=,即=,B′D=3,
此时D(3,0);
②∠B′DC=∠ABC,则△B′DC∽△ABC,可得:
=,即=,B′D=,
此时D(,0);
综上所述,存在符合条件的D点,且坐标为:D(3,0)或(,0).
【点睛】此题考查了二次函数解析式的确定、函数图象的平移、菱形的判定和性质、相似三角形的判定和性质等知识;(3)题中,在相似三角形的对应角和对应边不确定的情况下,一定要分类讨论,以免漏解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.5相似三角形的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列五幅图均是由边长为1的16个小正方形组成的正方形网格,网格中的三角形的顶点都在小正方形的顶点上,那么在下列左边四幅图中的三角形,与图中的△ABC相似的是( )
A. B. C. D.
2.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是( )
A. B. C. D.
3.如图,直角三角形中,,于,于,则下列说法中正确的有( )个.
①图中有4个三角形与相似;②;③;④;⑤若,,则;⑥.
A.2个 B.3个 C.4个 D.5个
4.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
5.如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
A.1:3 B.1:4 C.2:3 D.1:2
6.如图,中,于E.的长为( )
A.3 B. C. D.
7.的三边长分别为,,,的两边长分别为和,如果,那么的第三边长可能是下列数中的( )
A. B. C. D.
8.如图,半径为6的分别与轴,轴交于,两点,上两个动点,,使恒成立,设的重心为,则的最小值是( )
A. B. C. D.
9.和三角形三个顶点相连后,一定能把三角形分成面积相等的三部分的是该三角形的
A.内心 B.外心 C.重心 D.垂心
10.如图,在矩形ABCD中,点E是对角线上一点,连接AE并延长交CD于点F,过点E作EG⊥AE交BC于点G,若AB=8,AD=6,BG=2,则AE=( )
A. B. C. D.
11.如图,已知,点D是边中点,且.若( )
A.3 B.4
C. D.
12.如图,已知DE∥BC,CD和BE相交于点O,S△DOE∶S△COB=9∶16,则DE∶BC为( )
A.2∶3 B.3∶4 C.9∶16 D.1∶2
二、填空题
13.如图,点A、B分别在平面直角坐标系xOy的y轴正半轴、x轴正半轴上,且OA=4,OB=3,将△AOB沿AB折叠,O的落点为P,若双曲线y=过点P,则k= .
14.如图,已知矩形对角线和相交于点O,点E是边上一动点,与相交于点F,连结.
(1)若点E为的中点,则= ;
(2)若点F为的中点,则= .
15.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径弦于),设,,他用含的式子表示图中的弦的长度,通过比较运动的弦和与之垂直的直径的大小关系,发现了一个关于正数的不等式,你也能发现这个不等式吗?写出你发现的不等式 .
16.如图,AB是的直径,AD是的切线,点C在上,,,,则BC的长为 .
17.中,,,,,是直线,上的点.若由,,构成的三角形与相似,,则的长为 .
三、解答题
18.如图,已知梯形中,,对角线、交于.已知,.求: .
19.如图,已知矩形中,,点E在边上,的垂直平分线分别与边、相交于点F、G.
(1)若四边形能够成为菱形,则a必须满足的条件是_________;
(2)若,求的最小值;
(3)若经过点D、E、F的圆能够与直线、同时相切,求a的值.
20.已知:如图所示,在正方形ABCD中,F为DC的中点,E为BC上一点,且.求证:.
21.如图,AB与CD相交于点O,△OBD∽△OAC,=,OB=4,S△AOC=36,求
(1)AO的长.
(2)求S△BOD.
22.定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上动点,且AD=BE=CF.
求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=,求CF和AD的长.
23.已知等腰三角形ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F,
求证 :BE2=EF·EG.
24.如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
《6.5相似三角形的性质》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D B D A A B C B
题号 11 12
答案 D B
1.C
【分析】可利用正方形的边把对应的线段表示出来,利用三边对应成比例两个三角形相似,分别计算各边的长度即可解题.
【详解】解:根据勾股定理,,,
所以,夹直角的两边的比为,
观各选项,只有C选项三角形符合,与所给图形的三角形相似.
故选:C.
【点睛】此题考查了勾股定理在直角三角形中的运用,三角形对应边比值相等判定三角形相似的方法,本题中根据勾股定理计算三角形的三边长是解题的关键.
2.B
【详解】解:∵EF是点B、D的对称轴,
∴△BFE≌△DFE,
∴DE=BE.
∵在△BDE中,DE=BE,∠DBE=45°,
∴∠BDE=∠DBE=45°,
∴∠DEB=90°,
∴DE⊥BC.
在等腰梯形ABCD中,
∵=,
∴设AD=1,BC=4,过A作AG⊥BC于G,
∴四边形AGED是矩形,
∴GE=AD=1,
∵Rt△ABG≌Rt△DCE,
∴BG=EC=1.5,
∴AG=DE=BE=2.5,
∴AB=CD==,
∵∠ABC=∠C=∠FDE,∠CDE+∠C=90°,
∴∠FDE+∠CDE=90°,
∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°,
∴∠BDC=∠DFE,
∵∠DEF=∠DBC=45°,
∴△BDC∽△DEF,
∴,
∴DF=,
∴BF=,
∴AF=AB﹣BF=,
∴=.
故选B.
3.D
【分析】根据题意,对选项逐一分析,即可得出结论.
【详解】解:因为,,所以 =90°,=90°,所以=90°,可得,所以,所以,即,故选项②正确;
由题意,于,于E,所以=90°,,,,由相似的判定可知图中有4个三角形与相似,分别是、、、,故选项①正确;
因为,所以∠A与∠B互余,于,于,∠BCD与∠B互余,∠CDE与∠DCE互余,∠DCE与∠BCD互余,所以,故选项③正确;
因为,于,于,根据③中结论,所以,,因为,所以,两式相乘即可得,故选项④正确;
若,,由勾股定理可得AB=5,利用等面积可得,故选项⑤错误;
因为DE∥BC,所以,故选项⑥正确;
5个正确,
故答案为:D .
【点睛】本题考查了相似三角形的判定和性质,勾股定理的应用,余角的性质,熟练掌握相似三角形的判定和性质是解题的关键.
4.B
【分析】根据题意判断出△CBA∽△CAD,从而利用相似三角形的性质求解即可.
【详解】解:∵BC=8,AD是中线,
∴CD=BD=4,
在△CBA和△CAD中,
∵∠B=∠DAC,∠C=∠C,
∴△CBA∽△CAD,
∴,
∴AC2=CD BC=4×8=32,
∴AC=4;
故选:B.
【点睛】本题考查相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题关键.
5.D
【详解】解:在平行四边形ABCD中,AB∥DC,
则△DFE∽△BAE,
∴DF:AB=DE:EB.
∵O为对角线的交点,
∴DO=BO.
又∵E为OD的中点,
∴DE=DB,
则DE:EB=1:3,
∴DF:AB=1:3.
∵DC=AB,
∴DF:DC=1:3,
∴DF:FC=1:2.
故选D.
6.A
【分析】先证明,找出BE=2 DE,再利用勾股定理求解即可.
【详解】解:由题意知:∠BED=∠C,∠B=∠B,
∴,
∴,
∵,
∴,
∴BE=2DE,
由勾股定理知:,
代入计算得:BE=2,
又,
∴AE=5-2=3,
故答案为:A
【点睛】此题考查三角形相似,涉及到勾股定理求解,难度一般.
7.A
【分析】本题可根据相似三角形的性质:相似三角形的对应边成比例,来求出△DEF的第三边的长.
【详解】解:设△DEF的第三边长为x,
∵△ABC∽△DEF,
且△ABC的三边长分别为,,,△DEF的其中的两边长分别为1和,
∴==,
∴x=,
即:△DEF的第三边长为;
故选A.
【点睛】此题考查了相似三角形的性质,相似三角形的对应角相等,对应边的比相等.
8.B
【分析】连接AG并延长,交BC于点F,由△ABC的重心为G,可知F为BC的中点,再由垂径定理可知OF⊥BC,从而可求得OF的长;在AO上取点E,使AE=AO,连接GE,可判定△AGE∽△AFO,由相似三角形的性质列出比例式,求得GE的长,进而可得点E的坐标,利用勾股定理求出DE的长,根据G在以E为圆心,为半径的圆上运动,可知DG的最小值为DE的长减去,计算即可.
【详解】解:连接并延长,交于点,
的重心为,
为的中点,
,
,
,
,
,
的重心为,
,
在上取点,使,连接,
,,
,
,
.
在以为圆心,2为半径的圆上运动,
,,
,
的最小值是,
故选B.
【点睛】本题考查了三角形的重心、30°角所对的直角边等于斜边的一边、相似三角形的判定与性质、勾股定理在计算中的应用及勾股定理等知识点,熟练掌握相关性质及定理是解题的关键.
9.C
【分析】通过重心的性质和相似三角形得到S△OBC= S△ABC,同理可得S△OCA= S△ABC,S△OAB= S△ABC,问题得解.
【详解】解:如图,点O是△ABC的重心,
作△OBC的高OG和△ABC的高AH,
∴OG∥AH,
∴△OGD∽△AHD,
∴,
∴S△OBC= S△ABC,
同理可得:S△OCA= S△ABC,S△OAB= S△ABC
∴S△OBC= S△OCA = S△OAB,
∴一定能把三角形分成面积相等的三部分的是该三角形的重心,
故选C.
【点睛】本题考查三角形重心的定义和相似三角形的判定和性质,利用数形结合的思想是解决问题的关键.
10.B
【分析】过点作的平行线,分别交于点,先根据矩形的性质与判定可得四边形和四边形都是矩形,设,则,再根据相似三角形的判定证出,根据相似三角形的性质可得,从而可得,然后根据相似三角形的判定证出,根据相似三角形的性质可得的值,最后在中,利用勾股定理即可得.
【详解】解:如图,过点作的平行线,分别交于点,
四边形是矩形,,
,
四边形是矩形,
,
同理可得:四边形是矩形,
,
设,则,
,
,
,即,
解得,
,,
,
,
,
,
,
在和中,,
,
,即,
解得或,
经检验,是所列分式方程的根,且符合题意;不是所列分式方程的根,舍去,
,
,
故选:B.
【点睛】本题考查了矩形的判定与性质、相似三角形的判定与性质等知识点,通过作辅助线,构造相似三角形是解题关键.
11.D
【分析】由点D是边中点,得,再证明,得到,代入数值即可得到答案.
【详解】解:∵点D是边中点,
∴,
∵,,
∴,
∴,
∴,
∴,
∴(负值舍去),
故选:D
【点睛】此题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定是解题的关键.
12.B
【分析】首先根据平行得出三角形相似,然后根据相似三角形的面积之比等于相似比的平方得出答案.
【详解】∵DE∥BC, ∴△DOE∽△COB, ∴, ∴DE:BC=3:4,
故选B.
【点睛】本题主要考查的是相似三角形的性质,属于基础题型.明确相似三角形的面积之比等于相似比的平方是解题的关键.
13.
【分析】设P(x,y),过P作PD⊥x轴于D,过A作AC⊥PD于C,由垂直定义得∠AOB=∠ODC=∠C=90°,进而得∠PAC+∠APC=90°,再由折叠的性质得PA=OA=4,PB=OB=3,∠APB=90°,从而得∠APC+∠BPD=90°,∠BPD=∠PAC,进而证明△ACP∽△PDB,由相似三角形的性质即可求得点P的横、纵坐标,即可求解.
【详解】解:如图,设P(x,y),过P作PD⊥x轴于D,过A作AC⊥PD于C,
∵PD⊥x轴,AC⊥PD,x轴⊥y轴,
∴∠AOB=∠ODC=∠C=90°,
∴∠PAC+∠APC=90°,
∵OA=4,OB=3,将△AOB沿AB折叠,O的落点为P,
∴PA=OA=4,PB=OB=3,∠APB=90°,
∴∠APC+∠BPD=90°,
∴∠BPD=∠PAC,
∴△ACP∽△PDB
∴,即,
解得:x=,y=,
∵双曲线y=过点P,
∴k=×=.
故答案为:
【点睛】本题考查了坐标与图形,轴对称性质,正方形的性质,相似三角形的判定及性质,熟练掌握相似三角形的判定及性质是解题的关键.
14. /0.5 2
【分析】(1)根据矩形的性质可得点O是的中点,再结合已知可得是的中位线,从而可得,,然后证明8字模型相似三角形可得,利用相似三角形的性质进行计算即可解答;
(2)过作交于点,利用平行线分线段成比例和三角形全等即可求解.
【详解】(1)解:∵为矩形对角线交点,
∴.
∵点为中点,
∴为的中位线,
∴,,
∵,
∴,
∴;
(2)如图,过作交于点,
∴,
∴点为中点.
∴为的中位线,
∴,
∵,
∴.
又∵,,
∴,
∴,
∴,
即.
故答案为(1);(2)2.
【点睛】本题考查了相似三角形的判定与性质,矩形的性质以及全等三角形的判定和性质等,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
15.
【详解】解:连接AC,BD,
∵∠CAE=∠BDE,∠AEC=∠DEB,
∴△ACE∽△DBE,
∴,
∵CD⊥AB,
∴CE=DE,CD=2CE,
∴CE2=AE BE,
∴CE=.
∵CD=2CE,
∴CD=2CE=2.
又AB=x+y,且AB≥CD,得x+y≥2.
故答案为:x+y≥2.
16.
【分析】试题分析:根据圆周角定理可得∠C=90°,根据切线的性质可得∠OAD=90°,根据平行线的性质可得∠B=∠DOA,即可证得△OAD∽△BCA,最后根据相似三角形的性质求解即可.
【详解】∵AB是⊙O的直径,AD是⊙O的切线
∴∠C=90°,∠OAD=90°
∵BC//OD
∴∠B=∠DOA
∴△OAD∽△BCA
∴
∵AB=2,OD=3
∴,解得
故答案为
【点睛】本题考核知识点:圆周角定理,切线的性质,平行线的性质,相似三角形的判定和性质. 相似三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中半径常见的知识点.
17.或或或
【分析】由中,,,,,可求得的长,又由,,构成的三角形与相似,根据相似三角形的对应边成比例,即可求得的长.
【详解】∵△ABC中,BC=18,AC=12,AB=9,,
∴AE=4,
∵由A,D,E构成的三角形与△ABC相似,
∴当△ADE∽△ABC时,AD:AB=AE:AC=1:3,
∴
则BD=AB AD=6;
当△ADE∽△ACB时,AD:AC=AE:AB,
∴
∴
∴DB的长为:6或
当△ADE∽△ABC时,AD:AB=AE:AC=1:3,
∴
则BD=AB+AD=12;
当△ADE∽△ACB时,AD:AC=AE:AB,
∴
∴
综上所述:DB的长为:或或或
故答案为或或或.
【点睛】考查相似三角形的性质,注意分类讨论思想在解题中的应用.
18.16
【分析】由,可得 由可证 可得,根据即可计算出梯形ABCD的面积.
【详解】解:∵,
∴
∵
∴
∴
∴
∵
∴
【点睛】本题考查了相似比例与面积的关系,掌握面积间的关系是解题的关键.
19.(1);(2);(3).
【分析】(1)根据菱形的性质,找到E必在点D处,只要,那么形成的四边形必为菱形,就可求出a的取值范围;
(2)根据E点的运动过程,得到AF逐渐减小,即可得到当E在D时,最小,此时四边形为菱形;
(3)添加辅助线,过中点H作∥交AD于M,交BC于N,由题中所给已知条件可知,HN、EH、FH都是该圆的直径,用含a的式子表示HN和EF,再利用得出a的值
【详解】(1)
∵矩形,
∴BG∥DF
若四边形为菱形,则BG∥EF,
∴E必在点D处.
又,只要,那么形成的四边形必为菱形.
即.
(2)由运动规律可知,当E由C到D运动过程中,AF逐渐减小,所以当E在D时,最小,此时四边形为菱形.
设,则
∴
,解得,
即.
(3)如图所示,过中点H作∥交AD于M,交BC于N,
∵
∴H为过D、E、F的圆的圆心,EF为直径
∵经过点D、E、F的圆能够与直线、同时相切
∴,HN是半径
∵F在中垂线上,则
∴,(同角的余角相等),
∴
∴,
∴
又∵∥
∴
∴
∴
又
∴
又,则
∴
解得:.
【点睛】本题考查了菱形的性质和判定、勾股定理、全等三角形、圆的切线和相似三角形等相关知识,综合性较强.
20.见解析.
【分析】根据F为DC的中点,可得CE:DF=CF:AD=1:2,所以Rt△CEF∽Rt△DFA,然后根据相似三角形对应角相等可证出∠EFC+∠DFA=90°,即.
【详解】证明:∵四边形ABCD是正方形,
∴∠C=∠D=90°,
∵F是CD中点,
∴DF=CF=CD=AD,
∵CE=BC=CD,
∴CE:DF=CF:AD=1:2,
∴Rt△CEF∽Rt△DFA,
∴∠FAD=∠EFC,
∵∠FAD+∠DFA=90°,
∴∠EFC+∠DFA=90°,
∴∠EFA=90°,
∴AF⊥EF;
【点睛】本题考查了正方形的性质、相似三角形的判定和性质,根据题意得出CE:DF=CF:AD是解题关键.
21.(1)6;(2)16.
【分析】(1)由三角形相似可知,据此可求解;
(2)相似三角形的面积比等于相似比的平方.
【详解】解:(1)∵△OBD∽△OAC,
∴,
∵OB=4,
∴OA=6.
(2)∵△OBD∽△OAC,
∴,
∵S△AOC=36,
∴S△OBD=16.
【点睛】本题考查了相似三角形的性质以及相似比.
22.(1)证明见解析(2)2
【分析】(1)只要证明△DAF≌△EBD≌△FCE,可得DE=EF=DF,推出△DEF是等边三角形,推出∠DEF=∠EDF=∠B=∠A=60°,推出△DEF∽△ABC.可得△DEF是△ABC的子三角形;
(2)如图2中,作EH⊥AB于H.首先证明△DEF是等腰直角三角形,由△DEH≌△DFA,推出AD=HE,由△BEH是等腰直角三角形,推出HE=×=1,推出AD=1,由△BDE∽△CEF,可得,由此即可求出CF.
【详解】(1)证明:如图1中,
∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵AD=BE=CF,
∴AF=BD=CE,
∴△DAF≌△EBD≌△FCE,
∴DE=EF=DF,
∴△DEF是等边三角形,
∴∠DEF=∠EDF=∠B=∠A=60°,
∴△DEF∽△ABC.
∴△DEF是△ABC的子三角形.
(2)如图2中,作EH⊥AB于H.
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵△DEF是△ABC的子三角形,
∴△DEF∽△ABC,
∴DE=DF,∠EDF=90°,
∴∠ADF+∠AFD=90°,∠ADF+∠EDH=90°,
∴∠EDH=∠AFD,
∵∠DHE=∠A=90°,
∴△DEH≌△DFA,
∴AD=HE,
∵△BEH是等腰直角三角形,
∴HE=×=1,
∴AD=1,
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE,
∵∠B=∠DEF=45°,
∴△BDE∽△CEF,
∴,
∴CF=2.
【点睛】考查相似三角形的性质和判定、全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题.
23.见解析
【分析】先连接CE,由于AB=AC,AD⊥BC,利用等腰三角形三线合一定理可得BE=CE,再利用等边对等角可知∠EBC=∠ECB,易证∠ABE=∠ACE,结合CG∥AB,利用平行线的性质,可证∠CGF=∠FCE,再加上一组公共角,可证△CEF∽△GEC,于是CE2=EF·EG,从而得到BE2=EF·EG.
【详解】如图所示,连接EC,
∵AB=AC,AD⊥BC,
∴AD是∠BAC的角平分线,
∴BE=CE,
∴∠EBC=∠ECB,
又∵∠ABC=∠ACB,
∴∠ABC-∠EBC=∠ACB-∠ECB,
即∠ABE=∠ACE,
又∵CG∥AB,
∴∠ABE=∠CGF,
∴∠CGF=∠FCE,
又∠FEC=∠CEG,
∴△CEF∽△GEC,
∴CE2=EF·EG,
又CE=BE,
∴BE2=EF·EG.
【点睛】此题主要考查相似三角形的判定与性质,解题的关键是利用等腰三角形得到角度与线相等,从而解出此题.
24.(1)(2)(3)
【分析】(1)已知了抛物线图象上A、B两点的坐标,将它们代入抛物线的解析式中,即可求得m、n的值.
(2)根据A、B的坐标,易求得AB的长;根据平移的性质知:四边形A A′B′B一定为平行四边形,若四边形A A′B′B为菱形,那么必须满足AB=BB′,由此可确定平移的距离,根据“左加右减”的平移规律即可求得平移后的抛物线解析式.
(3)易求得直线AB′的解析式,联立平移后的抛物线对称轴,可得到C点的坐标,进而可求出AB、BC、AC、B′C的长;在(2)题中已经证得AB=BB′,那么∠BAC=∠BB′C,即A、B′对应,若以点B′、C、D为顶点的三角形与△ABC相似,可分两种情况考虑:①∠B′CD=∠ABC,此时△B′CD∽△ABC,②∠B′DC=∠ABC,此时△B′DC∽△ABC;
根据上述两种不同的相似三角形所得不同的比例线段,即可求得不同的BD长,进而可求得D点的坐标.
【详解】解:(1)由于抛物线经过A (﹣2,4)和点B (1,0),则有:
,解得;
故m=﹣,n=4.
(2)由(1)得:y=﹣x2﹣x+4=﹣(x+1)2+;
由A (﹣2,4)、B (1,0),可得AB==5;
若四边形A A′B′B为菱形,则AB=BB′=5,即B′(6,0);
故抛物线需向右平移5个单位,即:
y=﹣(x+1﹣5)2+=﹣(x﹣4)2+.
(3)由(2)得:平移后抛物线的对称轴为:x=4;
∵A(﹣2,4),B′(6,0),
∴直线AB′:y=﹣x+3;
当x=4时,y=1,故C(4,1);
所以:AC=3,B′C=,BC=;
由(2)知:AB=BB′=5,即∠BAC=∠BB′C;
若以点B′、C、D为顶点的三角形与△ABC相似,则:
①∠B′CD=∠ABC,则△B′CD∽△ABC,可得:
=,即=,B′D=3,
此时D(3,0);
②∠B′DC=∠ABC,则△B′DC∽△ABC,可得:
=,即=,B′D=,
此时D(,0);
综上所述,存在符合条件的D点,且坐标为:D(3,0)或(,0).
【点睛】此题考查了二次函数解析式的确定、函数图象的平移、菱形的判定和性质、相似三角形的判定和性质等知识;(3)题中,在相似三角形的对应角和对应边不确定的情况下,一定要分类讨论,以免漏解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
