第一单元观察物体(三)(知识梳理+拔高训练)二-2024-2025学年五年级数学下学期尖子生复习培优检测卷(人教版)
文档属性
| 名称 | 第一单元观察物体(三)(知识梳理+拔高训练)二-2024-2025学年五年级数学下学期尖子生复习培优检测卷(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 351.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-19 16:46:10 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第一单元观察物体(三)(知识梳理+拔高训练)二
知识梳理
知识点01:作简单图形的三视图
1、在画组合体三视图之前,首先运用形体分析法把组合体分解为若干个形体,确定它们的组合形式,判断形体间邻接表面是否处于共面、相切和相交的特殊位置;然后逐个画出形体的三视图;最后对组合体中的垂直面、一般位置面、邻接表面处于共面、相切或相交位置的面、线进行投影分析.当组合体中出现不完整形体、组合柱或复合形体相贯时,可用恢复原形法进行分析。
2、画哪个方向上的三视图就想象哪个方向上有光照到物体上,画出投影即可。
知识点02:三视图与展开图
1、三视图怎么看:
①从正面看,为主视图;②从侧面看,为左视图;③从上面看,为俯视图。
2、展开图为空间形体的表面在平面上摊平后得到的图形。
3、不同角度观察一个物体,看到的面都是两个或三个相邻的面。
4、不可能一次看到长方体或正方体相对的面。
注意点
1、这里所说的正面、左面和上面,都是相对于观察者而言的;
2、站在任意一个位置,最多只能看到长方体的3个面;
3、从不同的位置观察物体,看到的形状可能是不同的;
4、从一个或两个方向看到的图形是不能确定立体图形的形状的;
5、同一角度观察不同的立体图形,得到的平面图形可能是相同,也可能是不同的;
6、如果从物体的右面观察,看到的不一定和从左面看到的完全相同。
拔高训练
一、填空题(共20分)
1.(2分)《盲人摸象》的故事大家耳熟能详,说的是一群盲人摸一头大象,每个人把自己摸到的一个部位误认为是整体,后来人们便用“盲人摸象”来形容那些观察事物片面,只见局部不见整体的人,数学学习上也存在这样的问题,比如用6个同样的小正方体摆图形,如果要求从正面看到的是,你能确定这6个小正方体是怎样摆的吗?( )(填“能”或“不能”)
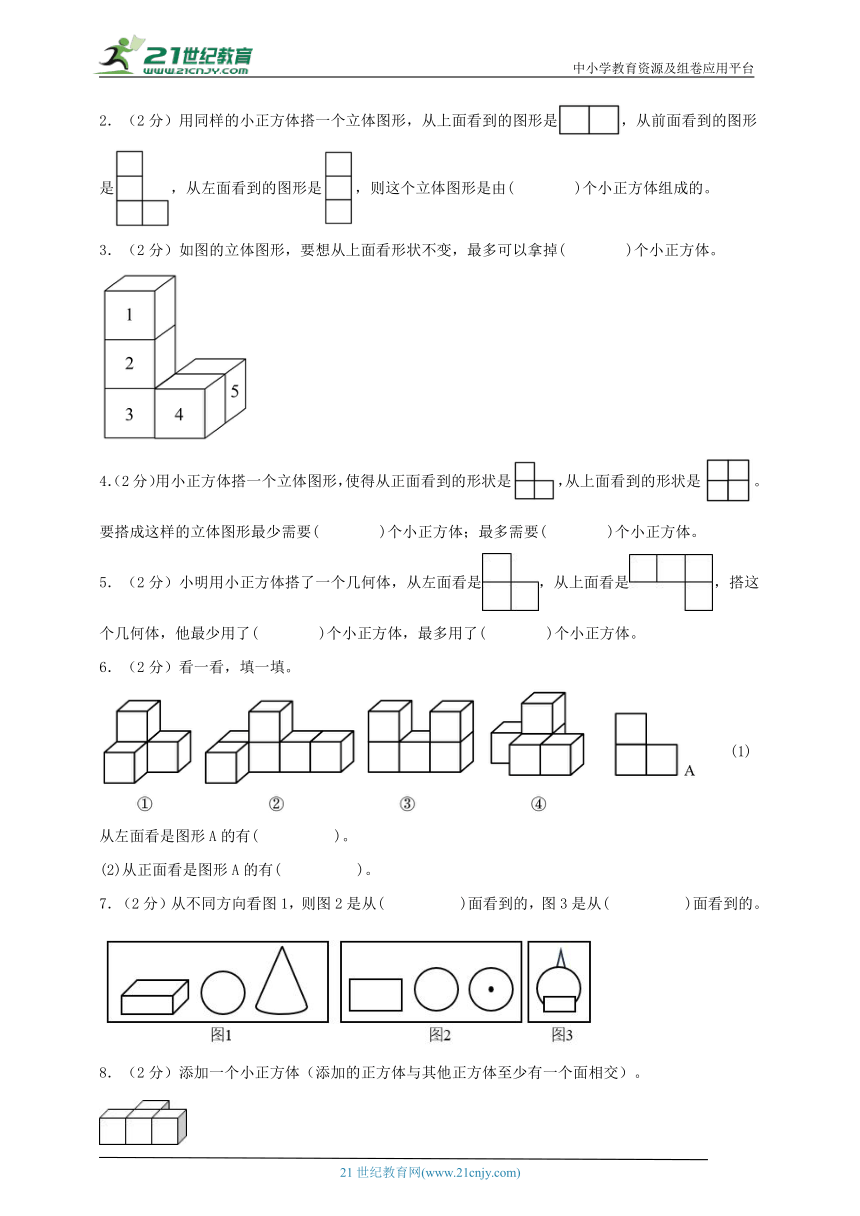
2.(2分)用同样的小正方体搭一个立体图形,从上面看到的图形是,从前面看到的图形是,从左面看到的图形是,则这个立体图形是由( )个小正方体组成的。
3.(2分)如图的立体图形,要想从上面看形状不变,最多可以拿掉( )个小正方体。
4.(2分)用小正方体搭一个立体图形,使得从正面看到的形状是,从上面看到的形状是。要搭成这样的立体图形最少需要( )个小正方体;最多需要( )个小正方体。
5.(2分)小明用小正方体搭了一个几何体,从左面看是,从上面看是,搭这个几何体,他最少用了( )个小正方体,最多用了( )个小正方体。
6.(2分)看一看,填一填。
(1)从左面看是图形A的有( )。
(2)从正面看是图形A的有( )。
7.(2分)从不同方向看图1,则图2是从( )面看到的,图3是从( )面看到的。
8.(2分)添加一个小正方体(添加的正方体与其他正方体至少有一个面相交)。
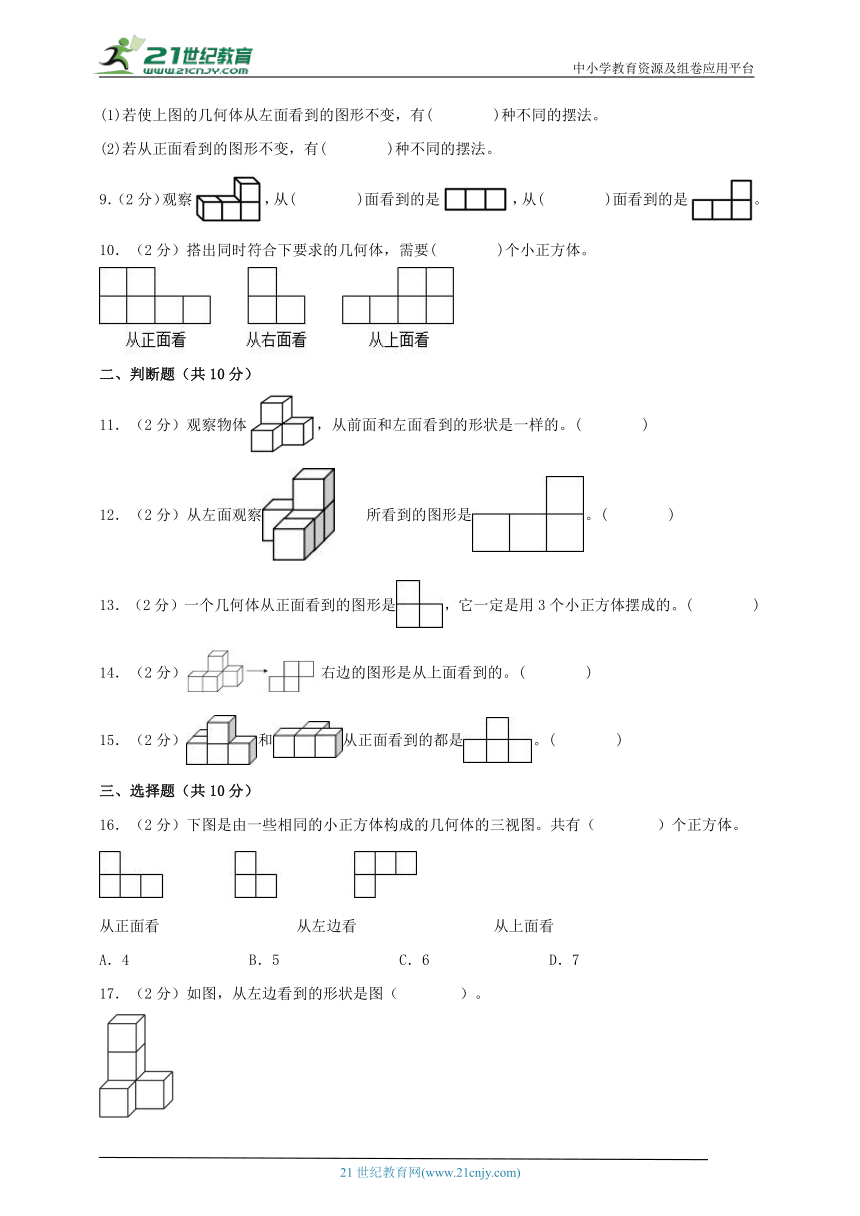
(1)若使上图的几何体从左面看到的图形不变,有( )种不同的摆法。
(2)若从正面看到的图形不变,有( )种不同的摆法。
9.(2分)观察,从( )面看到的是,从( )面看到的是。
10.(2分)搭出同时符合下要求的几何体,需要( )个小正方体。
二、判断题(共10分)
11.(2分)观察物体,从前面和左面看到的形状是一样的。( )
12.(2分)从左面观察 所看到的图形是。( )
13.(2分)一个几何体从正面看到的图形是,它一定是用3个小正方体摆成的。( )
14.(2分)右边的图形是从上面看到的。( )
15.(2分)和从正面看到的都是。( )
三、选择题(共10分)
16.(2分)下图是由一些相同的小正方体构成的几何体的三视图。共有( )个正方体。
从正面看 从左边看 从上面看
A.4 B.5 C.6 D.7
17.(2分)如图,从左边看到的形状是图( )。
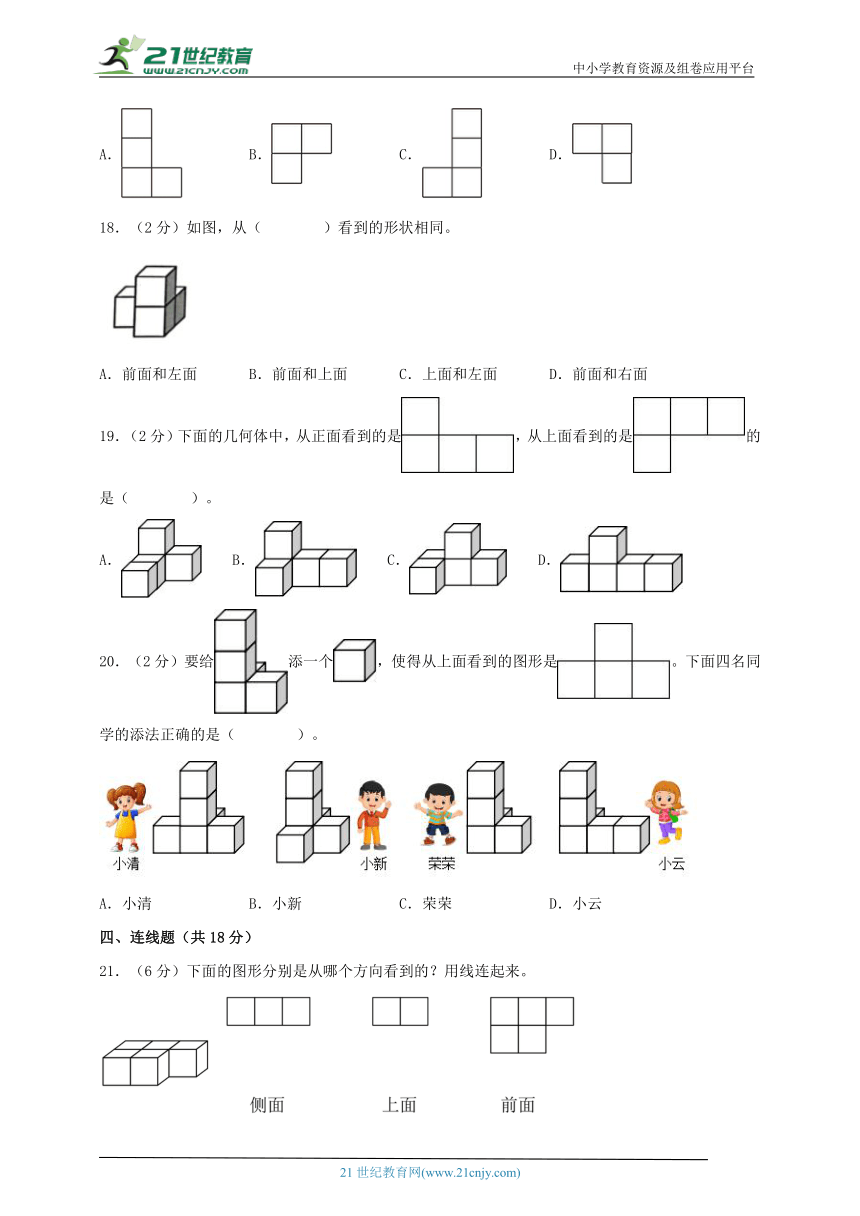
A. B. C. D.
18.(2分)如图,从( )看到的形状相同。
A.前面和左面 B.前面和上面 C.上面和左面 D.前面和右面
19.(2分)下面的几何体中,从正面看到的是,从上面看到的是的是( )。
A. B. C. D.
20.(2分)要给添一个,使得从上面看到的图形是。下面四名同学的添法正确的是( )。
A.小清 B.小新 C.荣荣 D.小云
四、连线题(共18分)
21.(6分)下面的图形分别是从哪个方向看到的?用线连起来。
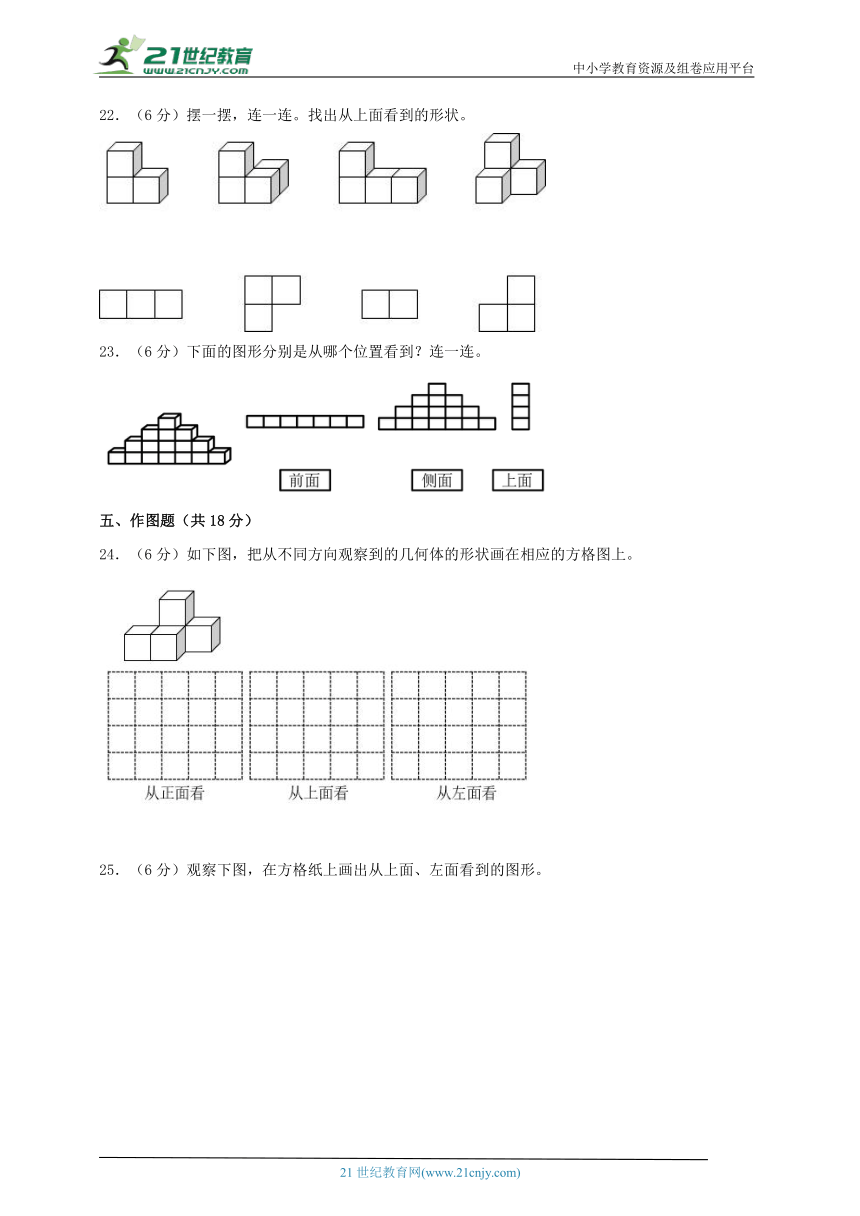
22.(6分)摆一摆,连一连。找出从上面看到的形状。
23.(6分)下面的图形分别是从哪个位置看到?连一连。
五、作图题(共18分)
24.(6分)如下图,把从不同方向观察到的几何体的形状画在相应的方格图上。
25.(6分)观察下图,在方格纸上画出从上面、左面看到的图形。
26.(6分)分别画出从正面、左面、上面看到的图形。
六、解答题(共24分)
27.(6分)如下图是从三个不同方向观察一个立体图形所看到的图形,最少需要多少个小正方体才能摆成的?试一试。
28.(6分)用4个同样的小正方体摆成几何体,并用下面的方法记录。如果再添上1个同样的小正方体(至少有1个面与其他小正方体相交),并使得整个几何体从正面看到的图形不变,那么有几种不同的摆法?按照下面的记录方式把各种摆法画下来。如果使从左面看到的图形不变呢?
从正面看图形不变: 从左面看图形不变:
29.(6分)下面的立体图形,从( )面看到的形状是完全相同的,请你把看到的形状画在下面的方格纸中。
30.(6分)用一些同样的正方体积木在桌面上摆一个几何体,要求从正面、上面和左面看到的图形都是,至少需要用几块正方体积木?最多呢?
参考答案
1.不能
【分析】用6个同样的小正方体摆图形,如果要求从正面看到的是,只能确定摆成的图形有2层,但每层摆小正方体的行数和每行的个数无法确定。
【详解】通过分析可得:用6个同样的小正方体摆图形,如果要求从正面看到的是,不能确定这6个小正方体是怎样摆的。
2.4
【分析】根据题意,从上面看到的图形是,可知底层分左右两列,有2个小正方体,结合从前面看到的图形是,从左面看到的图形是,可知左列有3个小正方体,右列有1个小正方体,据此解答即可。
【详解】3+1=4(个)
则这个立体图形是由4个小正方体组成的。
3.2
【分析】题中图形从上面看到的正方形有两行,共3个小正方形,上面1个,下面2个,右对齐,并且每个小正方形叠加的数量如图:
据此分析解答即可。
【详解】由分析可得:
要使从上面的形状不变,最多可以将做左边叠加3个的正方体,拿走2个。
综上所述:如图的立体图形,要想从上面看形状不变,最多可以拿掉2个小正方体。
【点睛】本题主要考查从不同方向观察物体,需要学生有空间想象能力,可以动手画图协助分析。
4. 5 6
【分析】根据从正面和上面看到的形状,这个立体图形有2层2行,上层至少有1个,最多有2个;下层有4个,据此得出这个立体图形最少和最多需要小正方体的个数。
【详解】如图:
要搭成这样的立体图形最少需要5个小正方体;最多需要6个小正方体。
【点睛】本题考查根据部分视图还原立体图形的能力,培养学生的空间想象力。
5. 5 7
【分析】根据从上面看到的平面图形可知,这个几何体的下层有4个小正方体;根据从左面看到的平面图形可知,这个几何体有2层,上层最少有1个,最多有3个,据此得出这个几何体最少和最多用到小正方体的个数。
【详解】如图:
搭这个几何体,他最少用了5个小正方体,最多用了7个小正方体。
【点睛】本题考查根据部分视图还原立体图形的能力,培养学生的空间想象力。
6.(1)①②④
(2)①
【分析】先观察题中四个几何体,再分别从正面、侧面观察这些物体,然后把观察到的形状分别与图形A对照做出选择。
【详解】(1)从左面看是图形A的有①②④。
(2)从正面看是图形A的有①。
【点睛】本题是考查从不同方向观察物体和几何图形,要求学生发挥观察能力和想象能力,能正确看出从正面、侧面、上面观察看到的平面图形,体验从不同的位置观察立体图形所看到的形状可能不同,关键是培养学生的观察能力。
7. 上 左
【分析】从上面看,可以看到左边是一个长方形,中间是一个圆,右边是一个中间有一个点的圆;
从左面看,圆挡住了三角形的一部分,长方形挡住了圆的一部分。据此解答。
【详解】由分析可知:从不同方向看图1,则图2是从上面看到的,图3是从左面看到的。
【点睛】本题考查从不同的方向观察物体。
8.(1)4
(2)6
【分析】(1)若使如图的几何体从左面看到的图形不变,则可以放在前面一行的左边或右边,或者放在后面一行的左边或右边,有4种摆法;
(2)若从正面看到的图形不变,则可以放在前面一行3个小正方体的任意一个的前面或后面,有6种摆法,据此即可解答问题;
【详解】(1)若使上图的几何体从左面看到的图形不变,有4种不同的摆法。
(2)若从正面看到的图形不变,有6种不同的摆法。
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
9. 上 正
【分析】观察图形可知,从正面看到的图形是2层,下层是3个正方形,上层1个正方形,靠右边;从上面看到的图形是1层,3个正方形排成1行;从左面看到的图形是2层,上、下各一个正方形,居中;由此解答。
【详解】根据分析可知,从上面看到的是,从正面看到的是。
【点睛】本题是考查从不同方向观察物体和几何体以及三视图的画法,目的是训练学生的观察能力。
10.8
【分析】根据观察题目中的三视图可知,这个几何体共有2层,下层一共有6个正方体,分两排,前排有4个,后排有2个,靠右;上层有2个正方体,在前排靠左。据此解答。
【详解】6+2=8(个)
据分析可知,搭建这个几何体一共要8个小正方体。
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
11.√
【分析】根据从前面和左面看到的形状判断即可。
【详解】从前面看:;从左面看:;据此可知,从前面和左面看到的形状是一样的。原题干说法正确。
故答案为:√
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
12.×
【分析】观察图形可知,从左面看到的图形有两层,第一层有3个小正方形,第二层有1个小正方形,靠左齐。据此解答即可。
【详解】由分析可知:
从左面观察到的图形是,所以原题干说法错误。
故答案为:×
【点睛】本题考查观察物体,明确从左面看到的形状是解题的关键。
13.×
【分析】这个立方体图形所用的小正方体分左右两列,左列有2层、每列、每层最少1个,多可无限,因此,一个几何体从左面看到的图形,这个几何体最少是由3个小正方体摆成的,多可无限个。
【详解】一个几何体从正面看到的图形是,它至少是用3个小正方体摆成的,多可无限个。
故答案为:×
【点睛】此题考查的是观察物体,解答此题应注意单从一个方向看不能确定所用小正方体的个数,要从前、左、上三个方向看才能确定所用小正方体的个数。
14.√
【分析】从上面看有2行,前边1行2个小正方形,后边1行错位2个小正方形。
【详解】右边的图形是从上面看到的,说法正确。
故答案为:√
【点睛】从不同方向观察物体常常得到不同的结果。
15.×
【分析】先画出这两个立体图形从正面看的图形,再判断正误即可。
【详解】从正面看是,从正面看是。
故答案为:×
【点睛】本题考查了观察物体,有一定空间观念是解题的关键。
16.B
【分析】从上面看可以确定这4个位置必须摆放正方体;从正面看需要保证左边第一列必须有一个位置是2层;再结合从左面看到的图形确定摆放2层的是哪个位置。
【详解】从上面看,按照如图标注的个数摆放,刚好满足题干中的三视图,此时需要的正方体是5个。
故答案为:B
【点睛】此题考查学生的空间想象能力,利用俯视图明确小正方体的摆放位置是解题的关键。
17.A
【分析】观察图形可知,从左边看到的图形有三层,第一层有2个正方形,第二层和第三层都有1个正方形,靠左齐。据此选择即可。
【详解】由分析可知:
从左边看到的形状是。
故答案为:A
【点睛】本题考查观察物体,明确从各方向观察到的形状是解题的关键。
18.A
【分析】分别画出该立体图形从前面、左面、上面、右面看到的平面图形,再根据画出的平面图形找出正确的选项,据此解答。
【详解】
由上可知,从前面和左面看到的形状相同。
故答案为:A
【点睛】本题主要考查物体三视图的认识,画出从不同方向看到的平面图形是解答题目的关键。
19.B
【分析】根据各选项从正面和上面看到的形状,找到符合题意的几何体即可。
【详解】A.从正面看到的是,从上面看到的是,不符合题干;
B.从正面看到的是,从上面看到的是,符合题干;
C.从正面看到的是,从上面看到的是,不符合题干;
D.从正面看到的是,从上面看到的是,不符合题干。
故答案为:B
【点睛】本题考查了从不同方向观察几何体,要有一定的空间想象能力。
20.A
【分析】根据观察,可知小清从上面看到的图形为;小新从上面看到的图形为 ;
荣荣从上面看到的图形为;小云从上面看到的图形为,据此解答。
【详解】由分析可知,要给添一个 ,使得从上面看到的图形是。
四名同学的添法正确的是小清。
故答案为:A。
【点睛】本题是考查从不同方向观察物体和几何体,关键是培养学生的观察能力。
21.见详解
【分析】这个立体图形由5个相同的小正方体组成,从前面能看到一行3个正方形,看到的是;从左面能看到一行2个正方形,看到的是;从右面能看到一行2个正方形,看到的是。从上面能看到5个正方形,分两层,下层2个,上层3个,看到的是。
【详解】
22.见详解
【分析】从左边起依次观察各个图形,第1个图形从上面看到一行,2个正方形。
第2个图形从上面看到两行,下面一行是2个正方形,上面一行是1个正方形,右对齐。
第3个图形从上面看到一行,3个正方形。
第4个图形从上面看到两行,上面一行是2个正方形,下面一行是1个正方形,左对齐。
【详解】
【点睛】本题考查了三视图的认识,需要学生有较强的空间想象和推理能力。
23.见详解
【分析】观察图形可知,从前面看到是4层,从下往上看第一层有7个长方形,第二层有5个长方形,居中摆放,第三层有3个长方形,居中摆放,第四层有1个长方形,居中摆放;从左侧面(或右侧面)看到的是1列,有4个长方形;从上面看到的是一排,有7个长方形;据此解题即可。
【详解】根据分析连线如下:
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和创新思维能力。
23.见详解
【分析】从正面看到了物体的长度和高度,从侧面看到了物体的宽度和高度,从上面看到了物体的长度和宽度。据此,再结合具体的立体图形,找出它从不同方向看到的图形即可。
【详解】如图:
【点睛】本题考查了观察物体,有一定空间观念是解题的关键。
24.见详解
【分析】根据几何体的特征,从正面看,能看到第一排有1个小正方形,第二排有并排的3个小正方形;从上面看,能看到第一排有并排的2个小正方形,第二排有2个小正方形;从左面看,能看到第一排有1个小正方形,第二排有2个小正方形,据此作出图形的三视图即可。
【详解】如图:
【点睛】本题考查从不同方向观察几何体,会作简单图形的三视图。
25.见详解
【分析】观察立体图形可知,从上面可以看到三列,左边一列可以看到2个小正方形,中间和右边一列各看到1个小正方形,三列小正方形顶部对齐;从左面可以看到两列,左边一列可以看到3个小正方形,右边一列可以看到1个小正方形,两列小正方形底部对齐,据此解答。
【详解】分析可知:
【点睛】掌握根据三视图画从不同方向看到平面图形的方法是解答题目的关键。
26.见详解
【分析】这个立体图形由5个相同的小正方体构成。从正面能看到5个正方形,分两层,下层有4个,上层有1个,位于上层右数第二个的上面;从左面能看到3个正方形,分两层,第一层有2个正方形,第二层有1个正方形,左齐;从上面能看到4个正方形,分两行,上行3个居左,下行1个居右,前后交错。
【详解】如图所示:
【点睛】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
27.5个
【分析】从上面看到的图形是物体的摆放位置,结合从正面看到的图形和从左面看到的图形,分析出每个位置摆放的小正方体的个数。
【详解】根据从正面看到的图可以判断这个图形有2层,第一层至少有3个,第二层至少有1个;根据从左面看到的图可以判断第一层至少有4个,第二层还是至少有1个;根据从上面看到的图可以判断第一层至少有2排,第一排至少有3个,第二排至少有1个。综上可得正方体排列的最少个数:,1+2+1+1=5(个)。
【点睛】要解决最少有多少个小正方体的问题,就要保证每个位置上既有小正方体,又得是个数最少的情况,可以拿学具摆一摆,通过动手操作,体会的更加深刻。
28.见详解
【分析】要想使从正面看到的图形不变,必须要做到不改变一行最多有2个小正方体的状态,也不改变左侧一列最高为两层、右侧一列只有一层的状态即可。
要想使从左面看到的图形不变,必须要做到不改变只有两行的状态,也不改变第二行有两层,第一行只有一层的状态即可。
【详解】从正面看图形不变:
从左面看图形不变:
【点睛】本题有一定的难度,解答本题时一定要抓住从正面看和左面看图形的特点,找到不变的点,再进行添加小正方体。
29.左;图见详解
【分析】分别画出三个立体图形的从三个面看到的图形,再进行解答即可。
【详解】从正面看是,从上面看是,从左边看是;
从正面看是,从上面看是,从左边看是;
从正面看是,从上面看是,从左边看是;
从左面看到的形状是完全相同的。
30.6块;8块
【分析】根据从上面看到的图形是, 可以知道底层需要4块积木,如图摆放: 。根据从正面看到的图形是 ,可以知道左右两列都有两层;根据从左面看到的图形是 ,可以知道在前后两行也都有两层。综合从正面和左面看到的图形可以知道第二层上至少应摆放2个小正方体,如图摆放: 、 ;最多可摆放4个小正方体,如图摆放:。
【详解】至少需要6块:、。
最多可摆放8个小正方体,如图摆放:。
答:至少需要用6块正方体积木,最多需要用8块正方体积木。
【点睛】本题考查观察物体,解答本题的关键是掌握根据从不同方向看到的图形确定物体形状的方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一单元观察物体(三)(知识梳理+拔高训练)二
知识梳理
知识点01:作简单图形的三视图
1、在画组合体三视图之前,首先运用形体分析法把组合体分解为若干个形体,确定它们的组合形式,判断形体间邻接表面是否处于共面、相切和相交的特殊位置;然后逐个画出形体的三视图;最后对组合体中的垂直面、一般位置面、邻接表面处于共面、相切或相交位置的面、线进行投影分析.当组合体中出现不完整形体、组合柱或复合形体相贯时,可用恢复原形法进行分析。
2、画哪个方向上的三视图就想象哪个方向上有光照到物体上,画出投影即可。
知识点02:三视图与展开图
1、三视图怎么看:
①从正面看,为主视图;②从侧面看,为左视图;③从上面看,为俯视图。
2、展开图为空间形体的表面在平面上摊平后得到的图形。
3、不同角度观察一个物体,看到的面都是两个或三个相邻的面。
4、不可能一次看到长方体或正方体相对的面。
注意点
1、这里所说的正面、左面和上面,都是相对于观察者而言的;
2、站在任意一个位置,最多只能看到长方体的3个面;
3、从不同的位置观察物体,看到的形状可能是不同的;
4、从一个或两个方向看到的图形是不能确定立体图形的形状的;
5、同一角度观察不同的立体图形,得到的平面图形可能是相同,也可能是不同的;
6、如果从物体的右面观察,看到的不一定和从左面看到的完全相同。
拔高训练
一、填空题(共20分)
1.(2分)《盲人摸象》的故事大家耳熟能详,说的是一群盲人摸一头大象,每个人把自己摸到的一个部位误认为是整体,后来人们便用“盲人摸象”来形容那些观察事物片面,只见局部不见整体的人,数学学习上也存在这样的问题,比如用6个同样的小正方体摆图形,如果要求从正面看到的是,你能确定这6个小正方体是怎样摆的吗?( )(填“能”或“不能”)
2.(2分)用同样的小正方体搭一个立体图形,从上面看到的图形是,从前面看到的图形是,从左面看到的图形是,则这个立体图形是由( )个小正方体组成的。
3.(2分)如图的立体图形,要想从上面看形状不变,最多可以拿掉( )个小正方体。
4.(2分)用小正方体搭一个立体图形,使得从正面看到的形状是,从上面看到的形状是。要搭成这样的立体图形最少需要( )个小正方体;最多需要( )个小正方体。
5.(2分)小明用小正方体搭了一个几何体,从左面看是,从上面看是,搭这个几何体,他最少用了( )个小正方体,最多用了( )个小正方体。
6.(2分)看一看,填一填。
(1)从左面看是图形A的有( )。
(2)从正面看是图形A的有( )。
7.(2分)从不同方向看图1,则图2是从( )面看到的,图3是从( )面看到的。
8.(2分)添加一个小正方体(添加的正方体与其他正方体至少有一个面相交)。
(1)若使上图的几何体从左面看到的图形不变,有( )种不同的摆法。
(2)若从正面看到的图形不变,有( )种不同的摆法。
9.(2分)观察,从( )面看到的是,从( )面看到的是。
10.(2分)搭出同时符合下要求的几何体,需要( )个小正方体。
二、判断题(共10分)
11.(2分)观察物体,从前面和左面看到的形状是一样的。( )
12.(2分)从左面观察 所看到的图形是。( )
13.(2分)一个几何体从正面看到的图形是,它一定是用3个小正方体摆成的。( )
14.(2分)右边的图形是从上面看到的。( )
15.(2分)和从正面看到的都是。( )
三、选择题(共10分)
16.(2分)下图是由一些相同的小正方体构成的几何体的三视图。共有( )个正方体。
从正面看 从左边看 从上面看
A.4 B.5 C.6 D.7
17.(2分)如图,从左边看到的形状是图( )。
A. B. C. D.
18.(2分)如图,从( )看到的形状相同。
A.前面和左面 B.前面和上面 C.上面和左面 D.前面和右面
19.(2分)下面的几何体中,从正面看到的是,从上面看到的是的是( )。
A. B. C. D.
20.(2分)要给添一个,使得从上面看到的图形是。下面四名同学的添法正确的是( )。
A.小清 B.小新 C.荣荣 D.小云
四、连线题(共18分)
21.(6分)下面的图形分别是从哪个方向看到的?用线连起来。
22.(6分)摆一摆,连一连。找出从上面看到的形状。
23.(6分)下面的图形分别是从哪个位置看到?连一连。
五、作图题(共18分)
24.(6分)如下图,把从不同方向观察到的几何体的形状画在相应的方格图上。
25.(6分)观察下图,在方格纸上画出从上面、左面看到的图形。
26.(6分)分别画出从正面、左面、上面看到的图形。
六、解答题(共24分)
27.(6分)如下图是从三个不同方向观察一个立体图形所看到的图形,最少需要多少个小正方体才能摆成的?试一试。
28.(6分)用4个同样的小正方体摆成几何体,并用下面的方法记录。如果再添上1个同样的小正方体(至少有1个面与其他小正方体相交),并使得整个几何体从正面看到的图形不变,那么有几种不同的摆法?按照下面的记录方式把各种摆法画下来。如果使从左面看到的图形不变呢?
从正面看图形不变: 从左面看图形不变:
29.(6分)下面的立体图形,从( )面看到的形状是完全相同的,请你把看到的形状画在下面的方格纸中。
30.(6分)用一些同样的正方体积木在桌面上摆一个几何体,要求从正面、上面和左面看到的图形都是,至少需要用几块正方体积木?最多呢?
参考答案
1.不能
【分析】用6个同样的小正方体摆图形,如果要求从正面看到的是,只能确定摆成的图形有2层,但每层摆小正方体的行数和每行的个数无法确定。
【详解】通过分析可得:用6个同样的小正方体摆图形,如果要求从正面看到的是,不能确定这6个小正方体是怎样摆的。
2.4
【分析】根据题意,从上面看到的图形是,可知底层分左右两列,有2个小正方体,结合从前面看到的图形是,从左面看到的图形是,可知左列有3个小正方体,右列有1个小正方体,据此解答即可。
【详解】3+1=4(个)
则这个立体图形是由4个小正方体组成的。
3.2
【分析】题中图形从上面看到的正方形有两行,共3个小正方形,上面1个,下面2个,右对齐,并且每个小正方形叠加的数量如图:
据此分析解答即可。
【详解】由分析可得:
要使从上面的形状不变,最多可以将做左边叠加3个的正方体,拿走2个。
综上所述:如图的立体图形,要想从上面看形状不变,最多可以拿掉2个小正方体。
【点睛】本题主要考查从不同方向观察物体,需要学生有空间想象能力,可以动手画图协助分析。
4. 5 6
【分析】根据从正面和上面看到的形状,这个立体图形有2层2行,上层至少有1个,最多有2个;下层有4个,据此得出这个立体图形最少和最多需要小正方体的个数。
【详解】如图:
要搭成这样的立体图形最少需要5个小正方体;最多需要6个小正方体。
【点睛】本题考查根据部分视图还原立体图形的能力,培养学生的空间想象力。
5. 5 7
【分析】根据从上面看到的平面图形可知,这个几何体的下层有4个小正方体;根据从左面看到的平面图形可知,这个几何体有2层,上层最少有1个,最多有3个,据此得出这个几何体最少和最多用到小正方体的个数。
【详解】如图:
搭这个几何体,他最少用了5个小正方体,最多用了7个小正方体。
【点睛】本题考查根据部分视图还原立体图形的能力,培养学生的空间想象力。
6.(1)①②④
(2)①
【分析】先观察题中四个几何体,再分别从正面、侧面观察这些物体,然后把观察到的形状分别与图形A对照做出选择。
【详解】(1)从左面看是图形A的有①②④。
(2)从正面看是图形A的有①。
【点睛】本题是考查从不同方向观察物体和几何图形,要求学生发挥观察能力和想象能力,能正确看出从正面、侧面、上面观察看到的平面图形,体验从不同的位置观察立体图形所看到的形状可能不同,关键是培养学生的观察能力。
7. 上 左
【分析】从上面看,可以看到左边是一个长方形,中间是一个圆,右边是一个中间有一个点的圆;
从左面看,圆挡住了三角形的一部分,长方形挡住了圆的一部分。据此解答。
【详解】由分析可知:从不同方向看图1,则图2是从上面看到的,图3是从左面看到的。
【点睛】本题考查从不同的方向观察物体。
8.(1)4
(2)6
【分析】(1)若使如图的几何体从左面看到的图形不变,则可以放在前面一行的左边或右边,或者放在后面一行的左边或右边,有4种摆法;
(2)若从正面看到的图形不变,则可以放在前面一行3个小正方体的任意一个的前面或后面,有6种摆法,据此即可解答问题;
【详解】(1)若使上图的几何体从左面看到的图形不变,有4种不同的摆法。
(2)若从正面看到的图形不变,有6种不同的摆法。
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力。
9. 上 正
【分析】观察图形可知,从正面看到的图形是2层,下层是3个正方形,上层1个正方形,靠右边;从上面看到的图形是1层,3个正方形排成1行;从左面看到的图形是2层,上、下各一个正方形,居中;由此解答。
【详解】根据分析可知,从上面看到的是,从正面看到的是。
【点睛】本题是考查从不同方向观察物体和几何体以及三视图的画法,目的是训练学生的观察能力。
10.8
【分析】根据观察题目中的三视图可知,这个几何体共有2层,下层一共有6个正方体,分两排,前排有4个,后排有2个,靠右;上层有2个正方体,在前排靠左。据此解答。
【详解】6+2=8(个)
据分析可知,搭建这个几何体一共要8个小正方体。
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
11.√
【分析】根据从前面和左面看到的形状判断即可。
【详解】从前面看:;从左面看:;据此可知,从前面和左面看到的形状是一样的。原题干说法正确。
故答案为:√
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
12.×
【分析】观察图形可知,从左面看到的图形有两层,第一层有3个小正方形,第二层有1个小正方形,靠左齐。据此解答即可。
【详解】由分析可知:
从左面观察到的图形是,所以原题干说法错误。
故答案为:×
【点睛】本题考查观察物体,明确从左面看到的形状是解题的关键。
13.×
【分析】这个立方体图形所用的小正方体分左右两列,左列有2层、每列、每层最少1个,多可无限,因此,一个几何体从左面看到的图形,这个几何体最少是由3个小正方体摆成的,多可无限个。
【详解】一个几何体从正面看到的图形是,它至少是用3个小正方体摆成的,多可无限个。
故答案为:×
【点睛】此题考查的是观察物体,解答此题应注意单从一个方向看不能确定所用小正方体的个数,要从前、左、上三个方向看才能确定所用小正方体的个数。
14.√
【分析】从上面看有2行,前边1行2个小正方形,后边1行错位2个小正方形。
【详解】右边的图形是从上面看到的,说法正确。
故答案为:√
【点睛】从不同方向观察物体常常得到不同的结果。
15.×
【分析】先画出这两个立体图形从正面看的图形,再判断正误即可。
【详解】从正面看是,从正面看是。
故答案为:×
【点睛】本题考查了观察物体,有一定空间观念是解题的关键。
16.B
【分析】从上面看可以确定这4个位置必须摆放正方体;从正面看需要保证左边第一列必须有一个位置是2层;再结合从左面看到的图形确定摆放2层的是哪个位置。
【详解】从上面看,按照如图标注的个数摆放,刚好满足题干中的三视图,此时需要的正方体是5个。
故答案为:B
【点睛】此题考查学生的空间想象能力,利用俯视图明确小正方体的摆放位置是解题的关键。
17.A
【分析】观察图形可知,从左边看到的图形有三层,第一层有2个正方形,第二层和第三层都有1个正方形,靠左齐。据此选择即可。
【详解】由分析可知:
从左边看到的形状是。
故答案为:A
【点睛】本题考查观察物体,明确从各方向观察到的形状是解题的关键。
18.A
【分析】分别画出该立体图形从前面、左面、上面、右面看到的平面图形,再根据画出的平面图形找出正确的选项,据此解答。
【详解】
由上可知,从前面和左面看到的形状相同。
故答案为:A
【点睛】本题主要考查物体三视图的认识,画出从不同方向看到的平面图形是解答题目的关键。
19.B
【分析】根据各选项从正面和上面看到的形状,找到符合题意的几何体即可。
【详解】A.从正面看到的是,从上面看到的是,不符合题干;
B.从正面看到的是,从上面看到的是,符合题干;
C.从正面看到的是,从上面看到的是,不符合题干;
D.从正面看到的是,从上面看到的是,不符合题干。
故答案为:B
【点睛】本题考查了从不同方向观察几何体,要有一定的空间想象能力。
20.A
【分析】根据观察,可知小清从上面看到的图形为;小新从上面看到的图形为 ;
荣荣从上面看到的图形为;小云从上面看到的图形为,据此解答。
【详解】由分析可知,要给添一个 ,使得从上面看到的图形是。
四名同学的添法正确的是小清。
故答案为:A。
【点睛】本题是考查从不同方向观察物体和几何体,关键是培养学生的观察能力。
21.见详解
【分析】这个立体图形由5个相同的小正方体组成,从前面能看到一行3个正方形,看到的是;从左面能看到一行2个正方形,看到的是;从右面能看到一行2个正方形,看到的是。从上面能看到5个正方形,分两层,下层2个,上层3个,看到的是。
【详解】
22.见详解
【分析】从左边起依次观察各个图形,第1个图形从上面看到一行,2个正方形。
第2个图形从上面看到两行,下面一行是2个正方形,上面一行是1个正方形,右对齐。
第3个图形从上面看到一行,3个正方形。
第4个图形从上面看到两行,上面一行是2个正方形,下面一行是1个正方形,左对齐。
【详解】
【点睛】本题考查了三视图的认识,需要学生有较强的空间想象和推理能力。
23.见详解
【分析】观察图形可知,从前面看到是4层,从下往上看第一层有7个长方形,第二层有5个长方形,居中摆放,第三层有3个长方形,居中摆放,第四层有1个长方形,居中摆放;从左侧面(或右侧面)看到的是1列,有4个长方形;从上面看到的是一排,有7个长方形;据此解题即可。
【详解】根据分析连线如下:
【点睛】此题考查了从不同方向观察物体和几何体,锻炼了学生的空间想象力和创新思维能力。
23.见详解
【分析】从正面看到了物体的长度和高度,从侧面看到了物体的宽度和高度,从上面看到了物体的长度和宽度。据此,再结合具体的立体图形,找出它从不同方向看到的图形即可。
【详解】如图:
【点睛】本题考查了观察物体,有一定空间观念是解题的关键。
24.见详解
【分析】根据几何体的特征,从正面看,能看到第一排有1个小正方形,第二排有并排的3个小正方形;从上面看,能看到第一排有并排的2个小正方形,第二排有2个小正方形;从左面看,能看到第一排有1个小正方形,第二排有2个小正方形,据此作出图形的三视图即可。
【详解】如图:
【点睛】本题考查从不同方向观察几何体,会作简单图形的三视图。
25.见详解
【分析】观察立体图形可知,从上面可以看到三列,左边一列可以看到2个小正方形,中间和右边一列各看到1个小正方形,三列小正方形顶部对齐;从左面可以看到两列,左边一列可以看到3个小正方形,右边一列可以看到1个小正方形,两列小正方形底部对齐,据此解答。
【详解】分析可知:
【点睛】掌握根据三视图画从不同方向看到平面图形的方法是解答题目的关键。
26.见详解
【分析】这个立体图形由5个相同的小正方体构成。从正面能看到5个正方形,分两层,下层有4个,上层有1个,位于上层右数第二个的上面;从左面能看到3个正方形,分两层,第一层有2个正方形,第二层有1个正方形,左齐;从上面能看到4个正方形,分两行,上行3个居左,下行1个居右,前后交错。
【详解】如图所示:
【点睛】本题是考查作简单图形的三视图,能正确辨认从正面、上面、左面(或右面)观察到的简单几何体的平面图形。
27.5个
【分析】从上面看到的图形是物体的摆放位置,结合从正面看到的图形和从左面看到的图形,分析出每个位置摆放的小正方体的个数。
【详解】根据从正面看到的图可以判断这个图形有2层,第一层至少有3个,第二层至少有1个;根据从左面看到的图可以判断第一层至少有4个,第二层还是至少有1个;根据从上面看到的图可以判断第一层至少有2排,第一排至少有3个,第二排至少有1个。综上可得正方体排列的最少个数:,1+2+1+1=5(个)。
【点睛】要解决最少有多少个小正方体的问题,就要保证每个位置上既有小正方体,又得是个数最少的情况,可以拿学具摆一摆,通过动手操作,体会的更加深刻。
28.见详解
【分析】要想使从正面看到的图形不变,必须要做到不改变一行最多有2个小正方体的状态,也不改变左侧一列最高为两层、右侧一列只有一层的状态即可。
要想使从左面看到的图形不变,必须要做到不改变只有两行的状态,也不改变第二行有两层,第一行只有一层的状态即可。
【详解】从正面看图形不变:
从左面看图形不变:
【点睛】本题有一定的难度,解答本题时一定要抓住从正面看和左面看图形的特点,找到不变的点,再进行添加小正方体。
29.左;图见详解
【分析】分别画出三个立体图形的从三个面看到的图形,再进行解答即可。
【详解】从正面看是,从上面看是,从左边看是;
从正面看是,从上面看是,从左边看是;
从正面看是,从上面看是,从左边看是;
从左面看到的形状是完全相同的。
30.6块;8块
【分析】根据从上面看到的图形是, 可以知道底层需要4块积木,如图摆放: 。根据从正面看到的图形是 ,可以知道左右两列都有两层;根据从左面看到的图形是 ,可以知道在前后两行也都有两层。综合从正面和左面看到的图形可以知道第二层上至少应摆放2个小正方体,如图摆放: 、 ;最多可摆放4个小正方体,如图摆放:。
【详解】至少需要6块:、。
最多可摆放8个小正方体,如图摆放:。
答:至少需要用6块正方体积木,最多需要用8块正方体积木。
【点睛】本题考查观察物体,解答本题的关键是掌握根据从不同方向看到的图形确定物体形状的方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
