2.5 有理数的乘方: 乘方的应用 课件(14张PPT) 2024-2025学年鲁教版(五四制)六年级数学上册
文档属性
| 名称 | 2.5 有理数的乘方: 乘方的应用 课件(14张PPT) 2024-2025学年鲁教版(五四制)六年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 11:32:06 | ||
图片预览






文档简介
(共14张PPT)
第二章 有理数及其运算
第5节 有理数的乘方
乘方的应用
2024新教材数学6年级上册
一.有理数的乘除、乘方的混合运算方法(重难点)
有理数的乘方运算比乘除运算更高一级,因此在进行它们的混合运算时,要先算乘方,后算乘除,有括号的先算括号里的,遇到高次乘方,要注意巧算:
(1)看底数是否互为倒数(或负倒数)的关系,如果不是,考虑是否可以转化为这种关系,从而约分化简现乘方。
(2)看底数是否出现相反数关系。
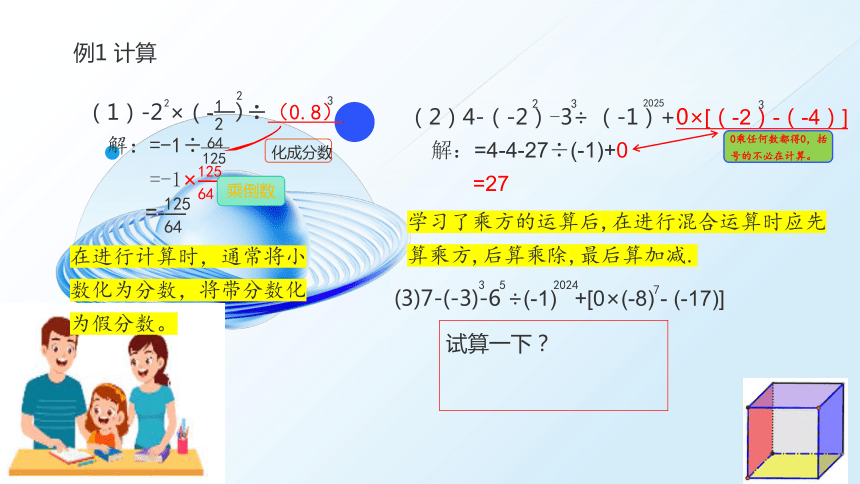
例1 计算
(1)-2 ×(-—)÷(0.8)
解:=-1÷
=-1×—
=-—
2
在进行计算时,通常将小数化为分数,将带分数化为假分数。
2
1
2
3
125
64
64
125
125
64
化成分数
乘倒数
(2)4-(-2)-3÷ (-1)+0×[(-2)-(-4)]
解:=4-4-27÷(-1)+0
=27
2
3
2025
3
0乘任何数都得0,括号的不必在计算。
学习了乘方的运算后,在进行混合运算时应先算乘方,后算乘除,最后算加减.
(3)7-(-3)-6 ÷(-1) +[0×(-8) - (-17)]
3
5
2024
7
试算一下?
(1)1的任何次幂都是1,-1的奇次幂是-1,偶次幂是1;
(2)互为相反数的两个数的偶次幂相等,奇次幂互为相反数.
方 法 归 纳
由于有理数的乘方运算是利用有理数的乘法法则进行的,故幂的符号可以利用有理数乘法的符号法则来确定。
易错警示
在进行乘方运算时,对乘方的意义理解不清,把乘方的意义与有理数的乘法混淆造成计算错误.
进行有理数运算时注意
二 学习有理数乘方的应用目的:
由于有理数乘方是数学中重要运算之一,它在几何学、物理学以及其他领域中都有广泛的应用.所以通过理解乘方的定义和性质,并运用到具体问题中,使我们能够更好地解决问题,得出正确的结论。
例1:
小明家有一桶 20 kg重的色拉油,他的妈妈每次都用去桶内油的一半,如此进行下去,那么第五次用完后桶内剩下多少千克色拉油
解题思路:第一次 20×-kg
第二次 20×-kg......第五次 20×-kg
2
1
2
1
2
1
解: 20×-=-=-(kg)
答:第五次用完后桶内剩下色拉油-kg.
1
2
5
32
20
5
8
5
8
例 题2
真实情境--生活情境1m长的木棒,第1次截去一半,第2次截去剩下的木棒的一半,如此截下去第6次截完后剩下的木棒有多长
分析:解决本题的关键是找出每次截完后剩下的木棒占整根木棒的比例与所截次数之间的关系。它们的关系列表如下:
解:6×(-) =-(m)
答:第6次截完后剩下的木棒长-m.
所截次数 1 2 3 4 5 6
剩下的点整根木棒的比例 -=(-) -=(-) -=(-) -=(-) -=(-) -=(-)
2
1
2
1
1
4
1
2
1
2
8
1
2
1
3
4
16
1
2
1
32
1
2
1
5
64
1
2
1
6
2
1
6
64
1
64
1
2、试解下题
1.某种细菌在培养过程中,每半小时分裂一次(由一个分裂成2个),若这种细菌由1个分裂成16个,则这个过程要经过多长时间?
解: 0.5小时/分2个,1小时/分4个 16个共分4次完成,
2 ×0.5=2(小时)
答要经过2小时完成。
2
三、找规律例题1.
观察下列各式:2 =2,2 =4,2 =8,2 =16, 2 = 32, 2 =67, 2=128
2 =256......通过观察,用你发现的规律写出2 的末位数字是 。
1
2
3
4
5
6
7
8
2024
解析:通过观察知这些数的末位数字每4个循环一次,以2 、4、8,6为一个循环,一直往后按规律出现。
因为2024÷4=506,所以2的2024次方的末位数字是6.
找规律例题2
观察下列等式:1 =1 ,1+2 =3 ,1+2+3 =6 1+2+3+4 =10
则1+2+3+4+5 =15
1+2+3+4+5+6 = 21 ???
3
2
3
3
3
3
3
3
2
3
3
3
3
2
3
3
3
3
3
3
3
3
3
3
3
解析:(1+2+3) =6 可知6 +4 =10 由此可推出1 、2题的结果
3
2
2
3
2
10
2
2
2
3.根据上两题解题
比较2023 与2024 的大小如何解?
2024
2023
为了解决这个问题,我们先把它抽象成这样的问题:写成它的一般形式,即比较(n+1) 和n 的大小(n是非零自然数),然后我们从n=1,
n=2,n=3,......这类简单情况入手,从而发现规律,经过归纳得出结论。
n+1
n
我们可以看到当底数大于1时幂的增长速度很快。
四、有理数乘方与其它知识的综合题型
1.若a和b互为相反数,x和y互为倒数,m的绝对值和倒数均是它本身,n的相反数是它本身,
求-(a +b )-9(-) +(-m) -n 的值?
分析:互为相反数的两个数的偶次幂相等,奇次幂仍互为相反数,所以当a和b互为相反数时,a + b =0。x和y互为倒数,则xy=1,所以m=1.相反数是它本身的数是0,所以n=0,由此可得:
5
1
2025
2024
xy
1
2024
2025
2023
2025
2024
解:=-×0-9×1 +(-1) -0
=0-9-1-0=-10
5
1
2024
2025
2023
-(a +b )-9(-) -(-m) -n
5
1
2025
2024
xy
1
2024
2025
2023
试着解下题
若(a-2)+ b+1 = 0 ,求(b-a) 的值?
2024
2
思考:1.若a ,b互为倒数,则2025-ab的值为 。
2.若定义一种新的运算”*“,规定有理数a * b=4ab,
如 2*3=4×2×3=24
(1)求3*(-4)的值
(2)求(-2)*(6*)的值
解题思路:因为2*3=4×2×3=24 *=24÷2÷=4 把它代入题中就可以算出值啦
谢 谢
第二章 有理数及其运算
第5节 有理数的乘方
乘方的应用
2024新教材数学6年级上册
一.有理数的乘除、乘方的混合运算方法(重难点)
有理数的乘方运算比乘除运算更高一级,因此在进行它们的混合运算时,要先算乘方,后算乘除,有括号的先算括号里的,遇到高次乘方,要注意巧算:
(1)看底数是否互为倒数(或负倒数)的关系,如果不是,考虑是否可以转化为这种关系,从而约分化简现乘方。
(2)看底数是否出现相反数关系。
例1 计算
(1)-2 ×(-—)÷(0.8)
解:=-1÷
=-1×—
=-—
2
在进行计算时,通常将小数化为分数,将带分数化为假分数。
2
1
2
3
125
64
64
125
125
64
化成分数
乘倒数
(2)4-(-2)-3÷ (-1)+0×[(-2)-(-4)]
解:=4-4-27÷(-1)+0
=27
2
3
2025
3
0乘任何数都得0,括号的不必在计算。
学习了乘方的运算后,在进行混合运算时应先算乘方,后算乘除,最后算加减.
(3)7-(-3)-6 ÷(-1) +[0×(-8) - (-17)]
3
5
2024
7
试算一下?
(1)1的任何次幂都是1,-1的奇次幂是-1,偶次幂是1;
(2)互为相反数的两个数的偶次幂相等,奇次幂互为相反数.
方 法 归 纳
由于有理数的乘方运算是利用有理数的乘法法则进行的,故幂的符号可以利用有理数乘法的符号法则来确定。
易错警示
在进行乘方运算时,对乘方的意义理解不清,把乘方的意义与有理数的乘法混淆造成计算错误.
进行有理数运算时注意
二 学习有理数乘方的应用目的:
由于有理数乘方是数学中重要运算之一,它在几何学、物理学以及其他领域中都有广泛的应用.所以通过理解乘方的定义和性质,并运用到具体问题中,使我们能够更好地解决问题,得出正确的结论。
例1:
小明家有一桶 20 kg重的色拉油,他的妈妈每次都用去桶内油的一半,如此进行下去,那么第五次用完后桶内剩下多少千克色拉油
解题思路:第一次 20×-kg
第二次 20×-kg......第五次 20×-kg
2
1
2
1
2
1
解: 20×-=-=-(kg)
答:第五次用完后桶内剩下色拉油-kg.
1
2
5
32
20
5
8
5
8
例 题2
真实情境--生活情境1m长的木棒,第1次截去一半,第2次截去剩下的木棒的一半,如此截下去第6次截完后剩下的木棒有多长
分析:解决本题的关键是找出每次截完后剩下的木棒占整根木棒的比例与所截次数之间的关系。它们的关系列表如下:
解:6×(-) =-(m)
答:第6次截完后剩下的木棒长-m.
所截次数 1 2 3 4 5 6
剩下的点整根木棒的比例 -=(-) -=(-) -=(-) -=(-) -=(-) -=(-)
2
1
2
1
1
4
1
2
1
2
8
1
2
1
3
4
16
1
2
1
32
1
2
1
5
64
1
2
1
6
2
1
6
64
1
64
1
2、试解下题
1.某种细菌在培养过程中,每半小时分裂一次(由一个分裂成2个),若这种细菌由1个分裂成16个,则这个过程要经过多长时间?
解: 0.5小时/分2个,1小时/分4个 16个共分4次完成,
2 ×0.5=2(小时)
答要经过2小时完成。
2
三、找规律例题1.
观察下列各式:2 =2,2 =4,2 =8,2 =16, 2 = 32, 2 =67, 2=128
2 =256......通过观察,用你发现的规律写出2 的末位数字是 。
1
2
3
4
5
6
7
8
2024
解析:通过观察知这些数的末位数字每4个循环一次,以2 、4、8,6为一个循环,一直往后按规律出现。
因为2024÷4=506,所以2的2024次方的末位数字是6.
找规律例题2
观察下列等式:1 =1 ,1+2 =3 ,1+2+3 =6 1+2+3+4 =10
则1+2+3+4+5 =15
1+2+3+4+5+6 = 21 ???
3
2
3
3
3
3
3
3
2
3
3
3
3
2
3
3
3
3
3
3
3
3
3
3
3
解析:(1+2+3) =6 可知6 +4 =10 由此可推出1 、2题的结果
3
2
2
3
2
10
2
2
2
3.根据上两题解题
比较2023 与2024 的大小如何解?
2024
2023
为了解决这个问题,我们先把它抽象成这样的问题:写成它的一般形式,即比较(n+1) 和n 的大小(n是非零自然数),然后我们从n=1,
n=2,n=3,......这类简单情况入手,从而发现规律,经过归纳得出结论。
n+1
n
我们可以看到当底数大于1时幂的增长速度很快。
四、有理数乘方与其它知识的综合题型
1.若a和b互为相反数,x和y互为倒数,m的绝对值和倒数均是它本身,n的相反数是它本身,
求-(a +b )-9(-) +(-m) -n 的值?
分析:互为相反数的两个数的偶次幂相等,奇次幂仍互为相反数,所以当a和b互为相反数时,a + b =0。x和y互为倒数,则xy=1,所以m=1.相反数是它本身的数是0,所以n=0,由此可得:
5
1
2025
2024
xy
1
2024
2025
2023
2025
2024
解:=-×0-9×1 +(-1) -0
=0-9-1-0=-10
5
1
2024
2025
2023
-(a +b )-9(-) -(-m) -n
5
1
2025
2024
xy
1
2024
2025
2023
试着解下题
若(a-2)+ b+1 = 0 ,求(b-a) 的值?
2024
2
思考:1.若a ,b互为倒数,则2025-ab的值为 。
2.若定义一种新的运算”*“,规定有理数a * b=4ab,
如 2*3=4×2×3=24
(1)求3*(-4)的值
(2)求(-2)*(6*)的值
解题思路:因为2*3=4×2×3=24 *=24÷2÷=4 把它代入题中就可以算出值啦
谢 谢
同课章节目录
