7.2 探索直线平行的条件 课件(共28张PPT)
文档属性
| 名称 | 7.2 探索直线平行的条件 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 984.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 09:05:11 | ||
图片预览


文档简介
(共28张PPT)
第七章 相交线与平行线
7.2探索直线平行的条件
1.会识别同位角、内错角、同旁内角。
2.经历探索直线平行条件的过程,掌握直线平行的条件,并能解决一些问题.
3.经历观察、操作、猜想、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达
的能力.
教学目标
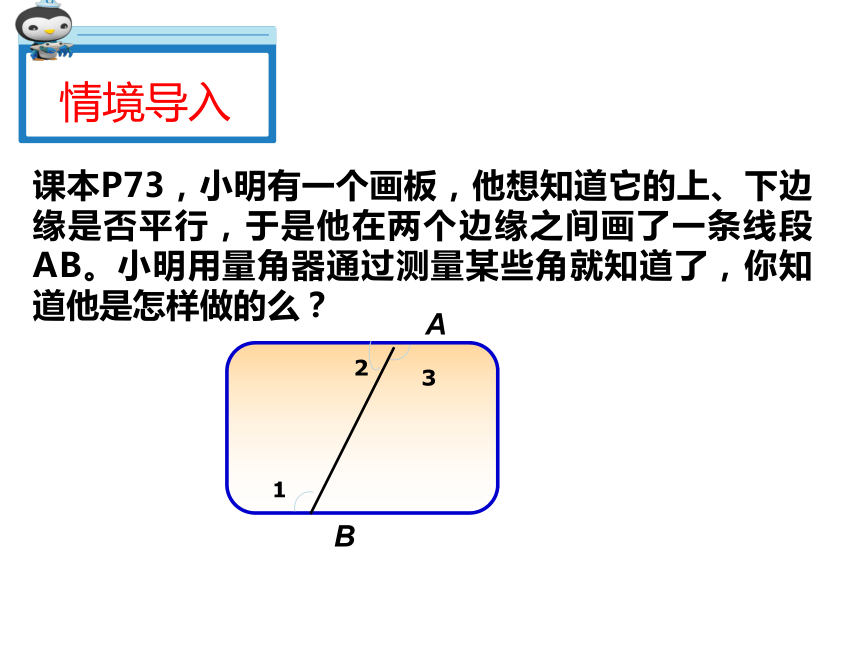
情境导入
课本P73,小明有一个画板,他想知道它的上、下边缘是否平行,于是他在两个边缘之间画了一条线段AB。小明用量角器通过测量某些角就知道了,你知道他是怎样做的么?
A
B
1
2
3
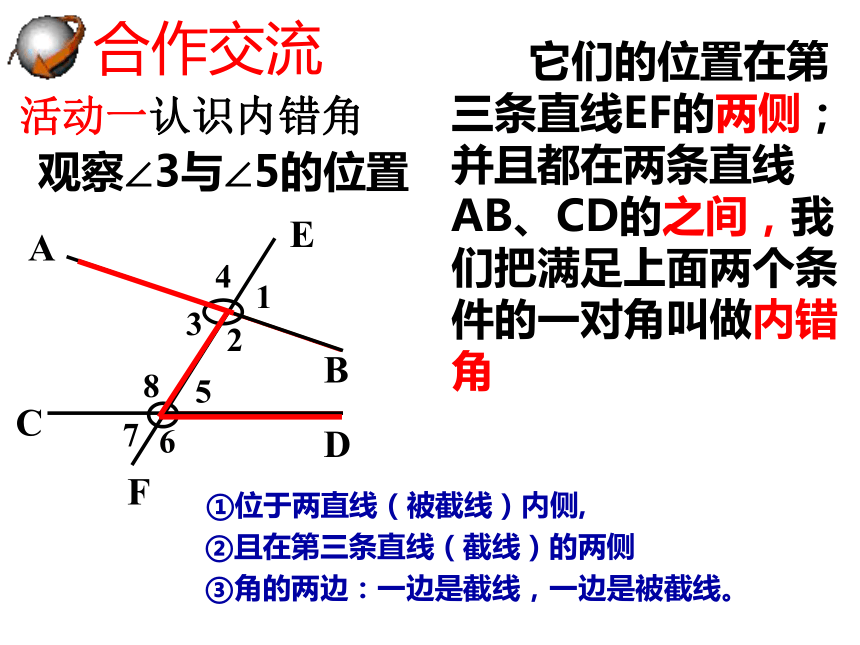
活动一认识内错角
合作交流
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察∠3与∠5的位置
它们的位置在第三条直线EF的两侧;并且都在两条直线AB、CD的之间,我们把满足上面两个条件的一对角叫做内错角
①位于两直线(被截线)内侧,
②且在第三条直线(截线)的两侧
③角的两边:一边是截线,一边是被截线。
A
B
D
E
F
1
2
3
4
5
6
7
8
C
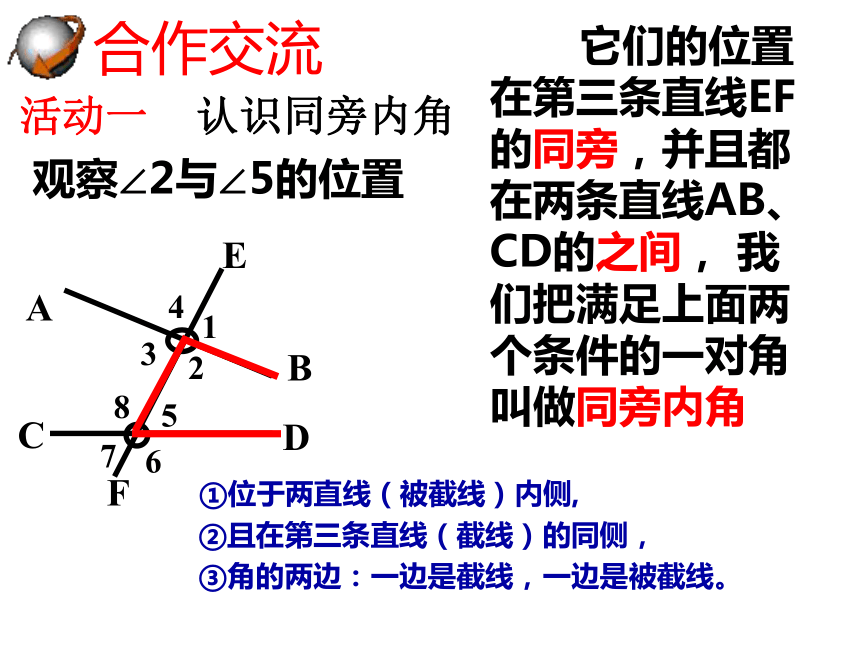
活动一 认识同旁内角
观察∠2与∠5的位置
它们的位置在第三条直线EF的同旁,并且都在两条直线AB、CD的之间, 我们把满足上面两个条件的一对角叫做同旁内角
①位于两直线(被截线)内侧,
②且在第三条直线(截线)的同侧,
③角的两边:一边是截线,一边是被截线。
合作交流
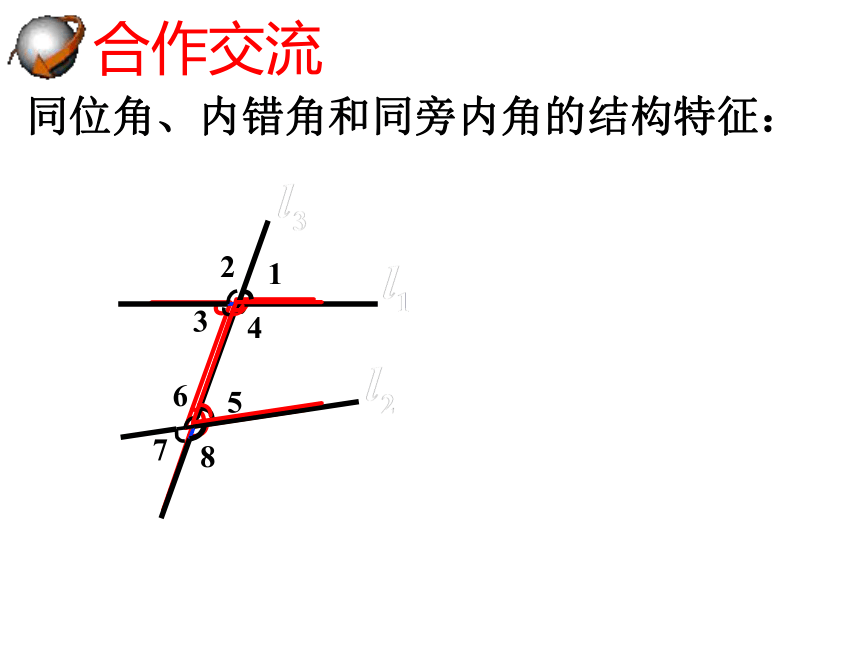
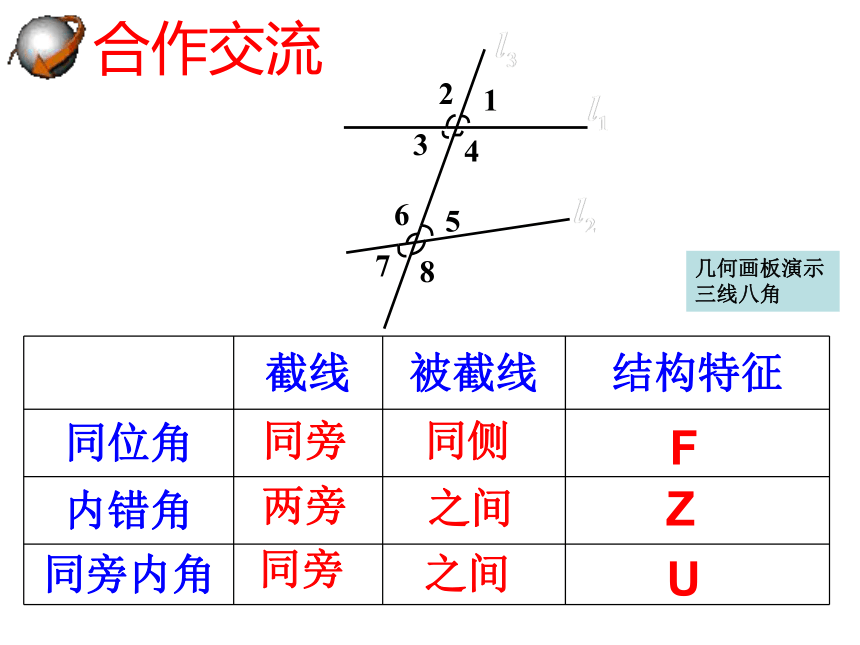
同位角、内错角和同旁内角的结构特征:
1
2
3
4
5
6
7
8
合作交流
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
1
2
3
4
5
6
7
8
几何画板演示三线八角
合作交流
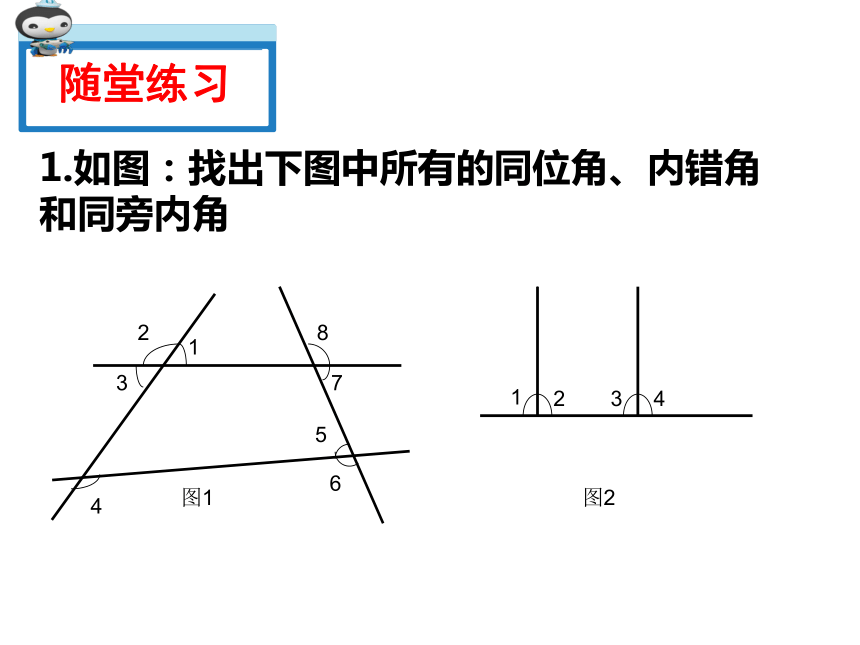
1.如图:找出下图中所有的同位角、内错角和同旁内角
1
2
3
4
5
6
7
8
图1
1
2
3
4
图2
随堂练习
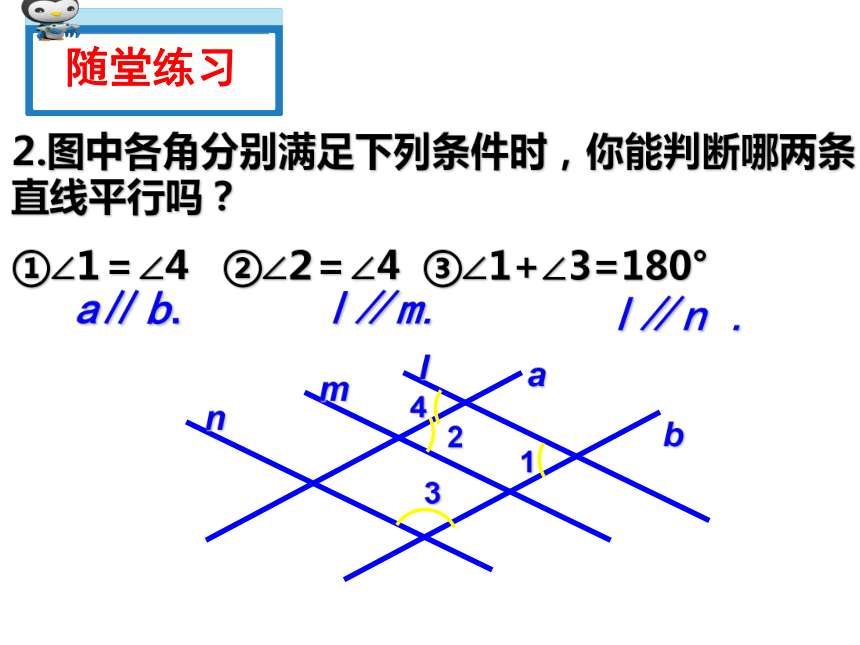
2.图中各角分别满足下列条件时,你能判断哪两条直线平行吗?
①∠1=∠4 ②∠2=∠4 ③∠1+∠3=180°
a
b
l
m
n
1
2
3
4
a∥b.
l∥m.
l∥n .
随堂练习
活动二探索直线平行的条件
㈠ 内错角满足什么关系时?两直线平行?
㈡ 同旁内角满足什么关系时?两直线平行?
为什么?
为什么?
合作交流
如图1,直线a,b被直线c所截,∠2=∠3,直线a与直线b平行吗?为什么?
3
2
1
a
b
c
合作交流
两条直线平行的条件之二:
内错角相等,两直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:
剖析:
1、“内错角相等”是条件,
“两直线平行”是结论;
2、作用:判定两直线平行;
3、符号语言:
因为 ∠1=∠2
所以 a∥b (内错角相等,两直线平行)
合作交流
∠1 = ∠3, ( )
探究1:为什么“内错角相等,两直线平行”
因为∠1 = ∠2,
( )
对顶角相等
已知
所以 ∠3 = ∠2. ( )
所以直线 a∥b. ( )
等量代换
同位角相等,两直线平行
b
a
c
1
2
3
内错角相等
同位角相等
两直线平行
如图2,直线a,b被直线c所截, ∠2+∠3=180,直线a与直线b平行吗?
为什么?
a
b
c
2
1
3
合作交流
两条直线平行的条件之三:
同旁内角互补,两直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:
剖析:
1、“同旁内角互补”是条件,
“两直线平行”是结论;
2、作用:判定两直线平行;
3、符号语言:
因为 ∠1+∠2=180°
所以 a∥b (同旁内角互补,两直线平行)
合作交流
∴ ∠3 = . ( )
∵ ∠1 ,∠2 , ( )
c
已知
∠1 ,∠3 , ( )
∴ 直线 a∥b. ( )
互补
∠2
同角的补角相等
内错角相等,两直线平行
内错角相等,两直线平行.
探究2:为什么“同旁内角互补,两直线平行”
互补
邻补角定义
b
a
2
3
1
还有其他推理的方法吗?
同旁内角互补
同位角相等
两直线平行
内错角相等
B
C
D
A
E
如图,三个相同的三角尺拼成一个图形,请找出图中的一组平行线,并说明你的理由.
AC与DE是平行的.
因为∠EDC与∠ACB
是同位角,
而且又相等.
我是这样想的:
∠BCA=∠EAC,
做一做
C
E
BC∥AE.
课堂小结
4
1
2
3
5
6
7
8
D
C
B
E
A
F
1. 再识“三线八角”:
4对同位角
∠1和∠5,
∠2和∠6,
∠3和∠7,
∠4和∠8.
2对内错角
∠3和∠5,
∠6和∠4.
2对同旁内角
∠5和∠4,
∠3和∠6.
2. 两直线平行的条件
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行.
3. 本节课运用了哪些数学思想方法
你有什么收获?
课堂小结
例1 如图,直线DE截直线AB,AC,构成8个角.指出所有的同位角、内错角和同旁内角.
截线
被截线
A
B
C
D
E
2
1
4
3
5
8
7
6
学以致用
练一练
(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角?
∠3与∠4呢?
∠ 2与∠4呢?
(同位角)
(内错角)
(同旁内角)
1
2
3
4
5
A
B
C
D
E
F
(2)如果把图看成是直线CD,EF被直线AB所截,那么∠1与∠5是一对什么角?
∠4与∠5呢?
(同旁内角)
(内错角)
1
2
3
4
5
A
B
C
D
E
F
练一练
(3)哪两条直线被哪一条直线所截,∠2与∠5是同位角?
(直线AB和CD被直线EF所截)
1
2
3
4
5
A
B
C
D
E
F
练一练
学以致用
例2 ∠1=∠2,∠B+∠BDE=180°.图中那些线互相平行为什么?
A
B
E
D
F
C
1
2
例3 如图,若∠1与∠2互补,∠2与∠3互补,你认为图形中有相互平行的直线吗?为什么
学以致用
l1
l3
l2
l4
l5
1
2
3
1、如图1,已知∠1=45°,∠2=135°,l1∥l2 吗?为什么?
分层训练
图1
2、如图2,一个弯形管道ABCD 的拐角∠ABC=110° , ∠BCD=70° ,这时管道 AB、 CD平行吗?
3、如图3,与∠A是同位角的有哪些角?与∠A为内错角有哪些?
分层训练
图2
图3
4、如图4,已知∠B=45°,∠C=135°,AB与CD平行吗?AD与BC平行吗?若不平行加上什么条件可使这两直线平行?
分层训练
图4
第七章 相交线与平行线
7.2探索直线平行的条件
1.会识别同位角、内错角、同旁内角。
2.经历探索直线平行条件的过程,掌握直线平行的条件,并能解决一些问题.
3.经历观察、操作、猜想、推理、交流等活动,进一步发展空间观念、推理能力和有条理表达
的能力.
教学目标
情境导入
课本P73,小明有一个画板,他想知道它的上、下边缘是否平行,于是他在两个边缘之间画了一条线段AB。小明用量角器通过测量某些角就知道了,你知道他是怎样做的么?
A
B
1
2
3
活动一认识内错角
合作交流
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察∠3与∠5的位置
它们的位置在第三条直线EF的两侧;并且都在两条直线AB、CD的之间,我们把满足上面两个条件的一对角叫做内错角
①位于两直线(被截线)内侧,
②且在第三条直线(截线)的两侧
③角的两边:一边是截线,一边是被截线。
A
B
D
E
F
1
2
3
4
5
6
7
8
C
活动一 认识同旁内角
观察∠2与∠5的位置
它们的位置在第三条直线EF的同旁,并且都在两条直线AB、CD的之间, 我们把满足上面两个条件的一对角叫做同旁内角
①位于两直线(被截线)内侧,
②且在第三条直线(截线)的同侧,
③角的两边:一边是截线,一边是被截线。
合作交流
同位角、内错角和同旁内角的结构特征:
1
2
3
4
5
6
7
8
合作交流
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
1
2
3
4
5
6
7
8
几何画板演示三线八角
合作交流
1.如图:找出下图中所有的同位角、内错角和同旁内角
1
2
3
4
5
6
7
8
图1
1
2
3
4
图2
随堂练习
2.图中各角分别满足下列条件时,你能判断哪两条直线平行吗?
①∠1=∠4 ②∠2=∠4 ③∠1+∠3=180°
a
b
l
m
n
1
2
3
4
a∥b.
l∥m.
l∥n .
随堂练习
活动二探索直线平行的条件
㈠ 内错角满足什么关系时?两直线平行?
㈡ 同旁内角满足什么关系时?两直线平行?
为什么?
为什么?
合作交流
如图1,直线a,b被直线c所截,∠2=∠3,直线a与直线b平行吗?为什么?
3
2
1
a
b
c
合作交流
两条直线平行的条件之二:
内错角相等,两直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简称:
剖析:
1、“内错角相等”是条件,
“两直线平行”是结论;
2、作用:判定两直线平行;
3、符号语言:
因为 ∠1=∠2
所以 a∥b (内错角相等,两直线平行)
合作交流
∠1 = ∠3, ( )
探究1:为什么“内错角相等,两直线平行”
因为∠1 = ∠2,
( )
对顶角相等
已知
所以 ∠3 = ∠2. ( )
所以直线 a∥b. ( )
等量代换
同位角相等,两直线平行
b
a
c
1
2
3
内错角相等
同位角相等
两直线平行
如图2,直线a,b被直线c所截, ∠2+∠3=180,直线a与直线b平行吗?
为什么?
a
b
c
2
1
3
合作交流
两条直线平行的条件之三:
同旁内角互补,两直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简称:
剖析:
1、“同旁内角互补”是条件,
“两直线平行”是结论;
2、作用:判定两直线平行;
3、符号语言:
因为 ∠1+∠2=180°
所以 a∥b (同旁内角互补,两直线平行)
合作交流
∴ ∠3 = . ( )
∵ ∠1 ,∠2 , ( )
c
已知
∠1 ,∠3 , ( )
∴ 直线 a∥b. ( )
互补
∠2
同角的补角相等
内错角相等,两直线平行
内错角相等,两直线平行.
探究2:为什么“同旁内角互补,两直线平行”
互补
邻补角定义
b
a
2
3
1
还有其他推理的方法吗?
同旁内角互补
同位角相等
两直线平行
内错角相等
B
C
D
A
E
如图,三个相同的三角尺拼成一个图形,请找出图中的一组平行线,并说明你的理由.
AC与DE是平行的.
因为∠EDC与∠ACB
是同位角,
而且又相等.
我是这样想的:
∠BCA=∠EAC,
做一做
C
E
BC∥AE.
课堂小结
4
1
2
3
5
6
7
8
D
C
B
E
A
F
1. 再识“三线八角”:
4对同位角
∠1和∠5,
∠2和∠6,
∠3和∠7,
∠4和∠8.
2对内错角
∠3和∠5,
∠6和∠4.
2对同旁内角
∠5和∠4,
∠3和∠6.
2. 两直线平行的条件
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行.
3. 本节课运用了哪些数学思想方法
你有什么收获?
课堂小结
例1 如图,直线DE截直线AB,AC,构成8个角.指出所有的同位角、内错角和同旁内角.
截线
被截线
A
B
C
D
E
2
1
4
3
5
8
7
6
学以致用
练一练
(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角?
∠3与∠4呢?
∠ 2与∠4呢?
(同位角)
(内错角)
(同旁内角)
1
2
3
4
5
A
B
C
D
E
F
(2)如果把图看成是直线CD,EF被直线AB所截,那么∠1与∠5是一对什么角?
∠4与∠5呢?
(同旁内角)
(内错角)
1
2
3
4
5
A
B
C
D
E
F
练一练
(3)哪两条直线被哪一条直线所截,∠2与∠5是同位角?
(直线AB和CD被直线EF所截)
1
2
3
4
5
A
B
C
D
E
F
练一练
学以致用
例2 ∠1=∠2,∠B+∠BDE=180°.图中那些线互相平行为什么?
A
B
E
D
F
C
1
2
例3 如图,若∠1与∠2互补,∠2与∠3互补,你认为图形中有相互平行的直线吗?为什么
学以致用
l1
l3
l2
l4
l5
1
2
3
1、如图1,已知∠1=45°,∠2=135°,l1∥l2 吗?为什么?
分层训练
图1
2、如图2,一个弯形管道ABCD 的拐角∠ABC=110° , ∠BCD=70° ,这时管道 AB、 CD平行吗?
3、如图3,与∠A是同位角的有哪些角?与∠A为内错角有哪些?
分层训练
图2
图3
4、如图4,已知∠B=45°,∠C=135°,AB与CD平行吗?AD与BC平行吗?若不平行加上什么条件可使这两直线平行?
分层训练
图4
同课章节目录
