7.3 平行线的性质 课件(共27张PPT)
文档属性
| 名称 | 7.3 平行线的性质 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 09:07:39 | ||
图片预览





文档简介
(共27张PPT)
第七章 相交线与平行线
六年级下册
3 平行线的性质
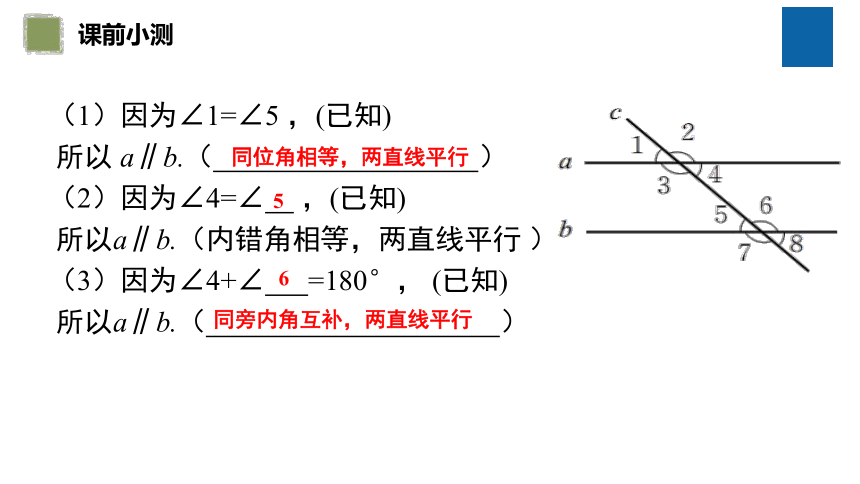
(1)因为∠1=∠5 ,(已知)
所以 a∥b.( )
(2)因为∠4=∠ ,(已知)
所以a∥b.(内错角相等,两直线平行 )
(3)因为∠4+∠ =180°, (已知)
所以a∥b.( )
同位角相等,两直线平行
5
6
同旁内角互补,两直线平行
课前小测
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
回想:平行线的判定定理有哪些呢?
思考:反过来,两条直线平行,同位角、内错角、同旁内角有什么样的关系?
情境导入
新知初探
贰
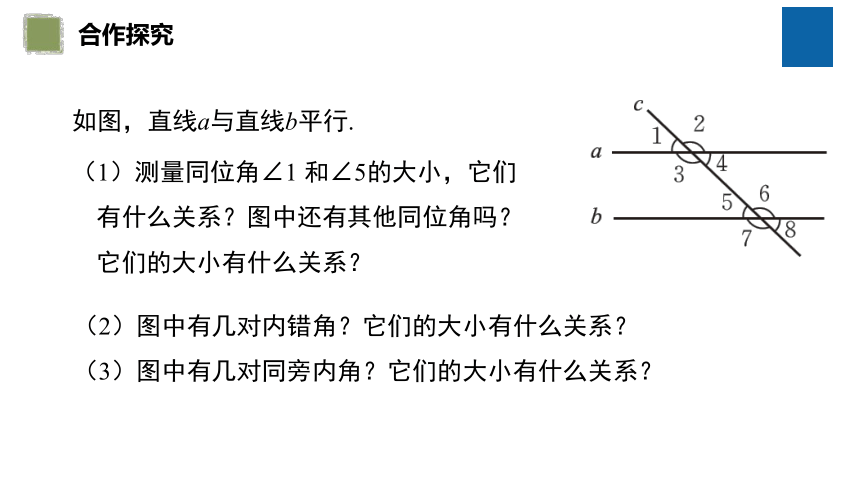
如图,直线a与直线b平行.
(1)测量同位角∠1 和∠5的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?
(2)图中有几对内错角?它们的大小有什么关系?
(3)图中有几对同旁内角?它们的大小有什么关系?
合作探究
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数
活动1:同学们可以先测量这些角的度数,把结果填入下表内.
活动2:请同学们根据测量所得的结果猜想:
同位角具有怎样的数量关系 内错角
具有怎样的数量关系 同旁内角呢?
动动小手
合作探究
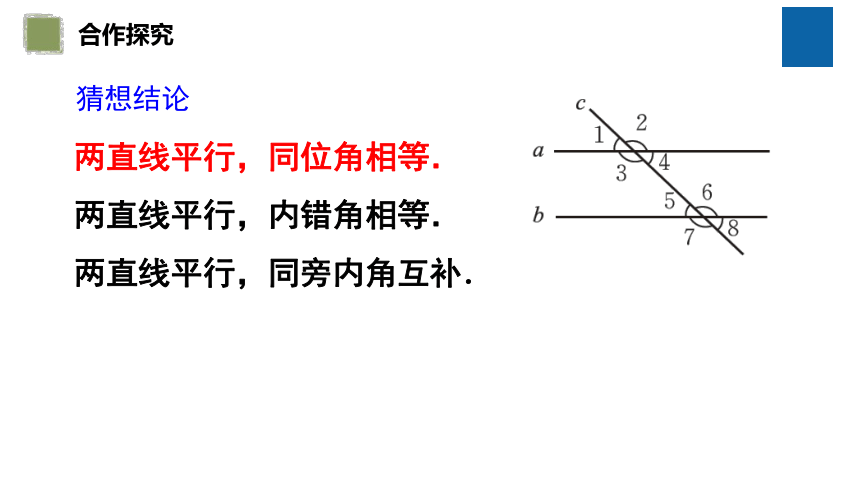
猜想结论
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
合作探究
活动3:另外画一组平行线被第三条直线所截,同样测量并计算各角的度数,检验刚才的猜想是否成立
如果直线a与b不平行,猜想还成立吗 试一试.
b
a
1
c
除了用测量的方法来说明直线平行,还有其他的方法吗?
验证猜想
合作探究
1
b
5
6
7
a
c
2
4
3
8
1
∠1=∠5
a∥b
裁剪叠合法
合作探究
平行线的性质:两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.
简记为
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
得出结论
合作探究
你能根据性质1,说出性质2,
性质3成立的理由吗
已知:a∥b,求证:∠4=∠5.
证明:∵a∥b,
∴∠1=∠5. ( )
又∵∠1=∠ ,(对顶角相等)
∴∠4=∠5.
同样,对于性质3,你能说出道理吗
两直线平行,同位角相等
4
运用推理
合作探究
已知:a∥b.
求证:∠3+∠5=180°.
证明:∵ a ∥ b ,(已知)
∴∠1=∠5,( )
又∵ ∠1+∠3=180°, ( )
∴ ∠3+∠5=180°.
两直线平行,同位角相等
邻补角的定义
(等量代换)
合作探究
对比学习
请大家填写下面的表格,加以对比:
条件 结论
判定直线 平行
平行线 的性质
同位角相等
两直线平行
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
合作探究
同位角相等
两直线平行 内错角相等
同旁内角互补
条件
性质
条件:角的关系 线的关系
性质:线的关系 角的关系
合作探究
如图,一束平行光线AB 与DE 射向一个水平 镜面后被反射,此时∠1 =∠2,∠3 =∠4.
(1)∠1 与∠3的大小有什么关系?
∠2与∠4 呢?
(2)反射光线BC与EF也平行吗?
联系拓广
合作探究
典例分析
例1 如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.
(1)解:∵直线DE∥OB,CF平分∠ACD,∠O=40°,
∴∠ACE=∠O,∠ACF=∠FCD,∴∠ACE=40°,
∴∠ACD=140°,∴∠ACF=70°,
∴∠ECF=∠ECA+∠ACF=40°+70°=110°;
(2)证明:∵CF平分∠ACD,CG⊥CF,∠ACD+∠OCD=180°,
∴∠ACF=∠FCD,∠FCG=90°,
∴∠FCD+∠DCG=90°,∠ACF+∠OCG=90°,
∴∠DCG=∠OCG,∴CG平分∠OCD.
典例分析
例2 如图是一块梯形铁片的残余部分,量得∠A = 100°,∠B = 115°,梯形的另外两个角的度数分别是多少?
解:∵已知与AB平行的一条边部分破损,∠A=120°,∠B=115°,
∴180°-∠A=60°,180°-∠B=65°
∴破损的另外两个角分别是60°,65°.
当堂达标
叁
当堂达标
1. 如图,直线∥2,直线与相交,若图中∠1=60°,则∠2为( )
A.30° B.40° C.50° D.60°
2.如图,四边形ABCD中,AD∥BC,∠A=110°,则∠B= .
D
70°
当堂达标
3.如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠C=135°,第二次拐的角∠B是多少度?
解:∵拐弯前后的两条路互相平行,第一次拐的角为∠C=135°,
∴∠B=∠C=135°.
当堂达标
4.如图,若∥ ,∥,请说出∠和∠之间的数量关系,并说明理由.
解:∠=∠.理由如下:
∵∥(已知),
∴∠=∠(两直线平行,同位角相等),
∵∥(已知),
∴∠=∠(两直线平行,同位角互等),
∴∠=∠(等量代换 ).
课堂小结
肆
课堂小结
1.平行线有哪些性质?
2.平行线的性质与平行线的判定方法之间的联系与区别.
作业布置
详见教材练习题
P83习题7.3.1
谢
谢
第七章 相交线与平行线
六年级下册
3 平行线的性质
(1)因为∠1=∠5 ,(已知)
所以 a∥b.( )
(2)因为∠4=∠ ,(已知)
所以a∥b.(内错角相等,两直线平行 )
(3)因为∠4+∠ =180°, (已知)
所以a∥b.( )
同位角相等,两直线平行
5
6
同旁内角互补,两直线平行
课前小测
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
回想:平行线的判定定理有哪些呢?
思考:反过来,两条直线平行,同位角、内错角、同旁内角有什么样的关系?
情境导入
新知初探
贰
如图,直线a与直线b平行.
(1)测量同位角∠1 和∠5的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?
(2)图中有几对内错角?它们的大小有什么关系?
(3)图中有几对同旁内角?它们的大小有什么关系?
合作探究
角 ∠1 ∠2 ∠3 ∠4 ∠5 ∠6 ∠7 ∠8
度数
活动1:同学们可以先测量这些角的度数,把结果填入下表内.
活动2:请同学们根据测量所得的结果猜想:
同位角具有怎样的数量关系 内错角
具有怎样的数量关系 同旁内角呢?
动动小手
合作探究
猜想结论
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
合作探究
活动3:另外画一组平行线被第三条直线所截,同样测量并计算各角的度数,检验刚才的猜想是否成立
如果直线a与b不平行,猜想还成立吗 试一试.
b
a
1
c
除了用测量的方法来说明直线平行,还有其他的方法吗?
验证猜想
合作探究
1
b
5
6
7
a
c
2
4
3
8
1
∠1=∠5
a∥b
裁剪叠合法
合作探究
平行线的性质:两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.
简记为
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
得出结论
合作探究
你能根据性质1,说出性质2,
性质3成立的理由吗
已知:a∥b,求证:∠4=∠5.
证明:∵a∥b,
∴∠1=∠5. ( )
又∵∠1=∠ ,(对顶角相等)
∴∠4=∠5.
同样,对于性质3,你能说出道理吗
两直线平行,同位角相等
4
运用推理
合作探究
已知:a∥b.
求证:∠3+∠5=180°.
证明:∵ a ∥ b ,(已知)
∴∠1=∠5,( )
又∵ ∠1+∠3=180°, ( )
∴ ∠3+∠5=180°.
两直线平行,同位角相等
邻补角的定义
(等量代换)
合作探究
对比学习
请大家填写下面的表格,加以对比:
条件 结论
判定直线 平行
平行线 的性质
同位角相等
两直线平行
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
合作探究
同位角相等
两直线平行 内错角相等
同旁内角互补
条件
性质
条件:角的关系 线的关系
性质:线的关系 角的关系
合作探究
如图,一束平行光线AB 与DE 射向一个水平 镜面后被反射,此时∠1 =∠2,∠3 =∠4.
(1)∠1 与∠3的大小有什么关系?
∠2与∠4 呢?
(2)反射光线BC与EF也平行吗?
联系拓广
合作探究
典例分析
例1 如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.
(1)解:∵直线DE∥OB,CF平分∠ACD,∠O=40°,
∴∠ACE=∠O,∠ACF=∠FCD,∴∠ACE=40°,
∴∠ACD=140°,∴∠ACF=70°,
∴∠ECF=∠ECA+∠ACF=40°+70°=110°;
(2)证明:∵CF平分∠ACD,CG⊥CF,∠ACD+∠OCD=180°,
∴∠ACF=∠FCD,∠FCG=90°,
∴∠FCD+∠DCG=90°,∠ACF+∠OCG=90°,
∴∠DCG=∠OCG,∴CG平分∠OCD.
典例分析
例2 如图是一块梯形铁片的残余部分,量得∠A = 100°,∠B = 115°,梯形的另外两个角的度数分别是多少?
解:∵已知与AB平行的一条边部分破损,∠A=120°,∠B=115°,
∴180°-∠A=60°,180°-∠B=65°
∴破损的另外两个角分别是60°,65°.
当堂达标
叁
当堂达标
1. 如图,直线∥2,直线与相交,若图中∠1=60°,则∠2为( )
A.30° B.40° C.50° D.60°
2.如图,四边形ABCD中,AD∥BC,∠A=110°,则∠B= .
D
70°
当堂达标
3.如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠C=135°,第二次拐的角∠B是多少度?
解:∵拐弯前后的两条路互相平行,第一次拐的角为∠C=135°,
∴∠B=∠C=135°.
当堂达标
4.如图,若∥ ,∥,请说出∠和∠之间的数量关系,并说明理由.
解:∠=∠.理由如下:
∵∥(已知),
∴∠=∠(两直线平行,同位角相等),
∵∥(已知),
∴∠=∠(两直线平行,同位角互等),
∴∠=∠(等量代换 ).
课堂小结
肆
课堂小结
1.平行线有哪些性质?
2.平行线的性质与平行线的判定方法之间的联系与区别.
作业布置
详见教材练习题
P83习题7.3.1
谢
谢
同课章节目录
