北师大版数学七年级下册第四章三角形4.3探索三角形全等的条件课时练习
文档属性
| 名称 | 北师大版数学七年级下册第四章三角形4.3探索三角形全等的条件课时练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-17 00:00:00 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
北师大版数学七年级下册第四章4.3探索三角形全等的条件课后练习
一,选择题(共15题)
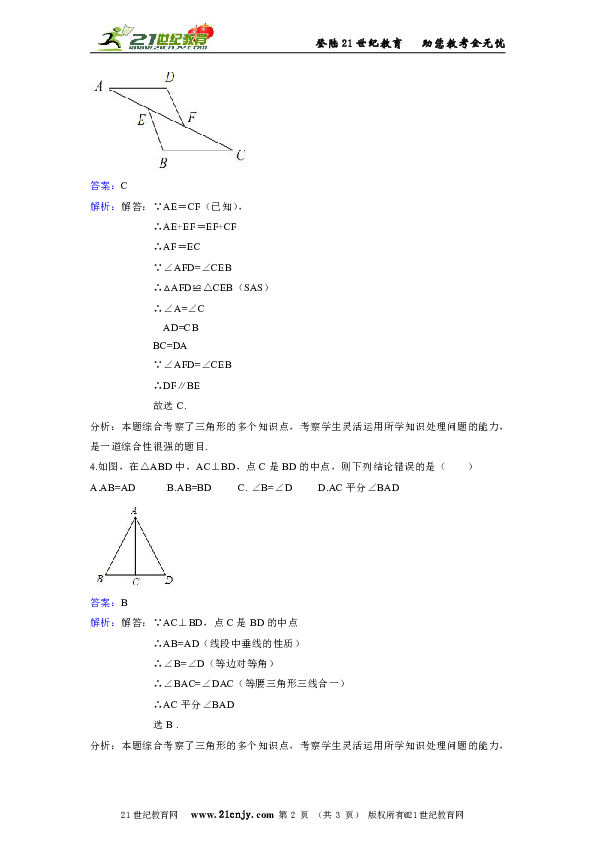
1. 如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
答案:B
解析:解答:∵AB=AD (已知),AC=AC(公共边)
∴只需要BAC=∠DAC
∴△ABE≌△ACD
故选B.
分析:本题考察了全等三角形的判定方法中的SAS,较为简单.
2.如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
答案:C
解析:解答:∵AB=AC (已知),∠A=∠A(公共角)
∴只需要AE=AD
∴△ABE≌△ACD
故选C.
分析:本题考察了全等三角形的判定方法中的SAS,较为简单.
3. 如图,已知E,F是AC上的两点,AE=CF,DF=BE,∠AFD=∠CEB,则下列不成立的是( )
A.∠A=∠C B.AD=CB C.BC=DF D.DF∥BE
答案:C
解析:解答:∵AE=CF(已知),
∴AE+EF=EF+CF
∴AF=EC
∵∠AFD=∠CEB
∴△AFD≌△CEB(SAS)
∴∠A=∠C
AD=CB
BC=DA
∵∠AFD=∠CEB
∴DF∥BE
故选C.
分析:本题综合考察了三角形的多个知识点,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
4.如图,在△ABD中,AC⊥BD,点C是BD的中点,则下列结论错误的是( )
A.AB=AD B.AB=BD C. ∠B=∠D D.AC平分∠BAD
答案:B
解析:解答:∵AC⊥BD,点C是BD的中点
∴AB=AD(线段中垂线的性质)
∴∠B=∠D(等边对等角)
∴∠BAC=∠DAC(等腰三角形三线合一)
∴AC平分∠BAD
选B .
分析:本题综合考察了三角形的多个知识点,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
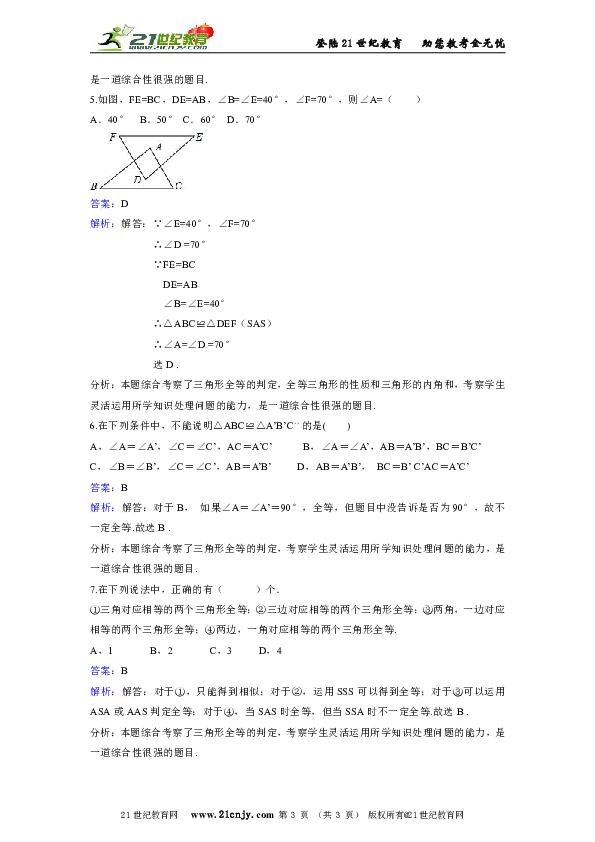
5.如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
A.40° B.50° C.60° D.70°
答案:D
解析:解答:∵∠E=40°,∠F=70°
∴∠D =70°
∵FE=BC
DE=AB
∠B=∠E=40°
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°
选D .
分析:本题综合考察了三角形全等的判定,全等三角形的性质和三角形的内角和,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
6.在下列条件中,不能说明△ABC≌△A’B’C,,的是( )
A,∠A=∠A’,∠C=∠C’,AC=A’C’ B,∠A=∠A’,AB=A’B’,BC=B’C’
C,∠B=∠B’,∠C=∠C’,AB=A’B’ D,AB=A’B’, BC=B’ C’AC=A’C’
答案:B
解析:解答:对于B, 如果∠A=∠A’=90°,全等,但题目中没告诉是否为90°,故不一定全等.故选B .
分析:本题综合考察了三角形全等的判定,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
7.在下列说法中,正确的有( )个.
①三角对应相等的两个三角形全等;②三边对应相等的两个三角形全等;③两角,一边对应相等的两个三角形全等;④两边,一角对应相等的两个三角形全等.
A,1 B,2 C,3 D,4
答案:B
解析:解答:对于①,只能得到相似;对于②,运用SSS可以得到全等;对于③可以运用ASA或AAS判定全等;对于④,当SAS时全等,但当SSA时不一定全等.故选B .
分析:本题综合考察了三角形全等的判定,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
8.下列说法正确的是( )
A,两个周长相等的长方形全等 B,两个周长相等的三角形全等
C,两个面积相等的长方形全等 D,两个周长相等的圆全等
答案:D
解析:解答:对于两个图形,只有知道两个圆的半径相等,则这两个圆就全等,其余选项,皆不能得到全等,故选D .
分析:本题综合考察了全等图形的判定,结合了上一节内容,考察学生灵活处理问题的能力.
9. 使两个直角三角形全等的条件是( )
A. 一锐角对应相等 B. 两锐角对应相等
C. 一条边对应相等 D. 两条边对应相等
答案:D
解析:解答:对于两个直角三角形,已经知道有一组角对应相等了,因此,运用HL定理可以判定两个直角三角形全等,选D .
分析:本题综合考察了全等三角形的判定中的HL定理,内容简单.
10.如图,分别为的,边的中点,将此三角形沿折叠,使点落在边上的点处.若,则等于( )
A. B. C . D.
答案:B
解析:解答: 由翻折得△PDE≌△CDE
∴∠PDE=∠CDE=48°
∵分别为的,边的中点,
∴D E∥AB
∴∠APD=∠PDE=48°
∴选B.
分析:本题综合考察了全等三角形的性质,三角形的中位线定理和平行线的性质,考察知识点较多,是一道不错的题目.
11. 如图,△ABC≌△CDA,且AD=CB,下列结论错误的是( )
A,∠B=∠D B,∠CAB=∠ACD C,BC=CD D,AC=CA
答案:C
解析:解答: ∵△ABC≌△CDA,且AD=CB
∴∠B=∠D
∠CAB=∠ACD
AC=CA
∴选C.
分析:本题综合考察了全等三角形的性质,考察知识点较多,是一道不错的题目.
12.已知:如图,AC=CD ,∠B=∠E=90°, AC⊥CD,则不正确的结论是 ( )
A,∠A与∠D互为余角 B,∠A=∠2
C,△ABC≌△CED D,∠1=∠2
答案:D
解析:解答: ∵AC⊥CD
∴∠ACD=90°
∵∠1+∠2+∠ACD=180°
∴∠1+∠2=90°
∴选D.
分析:本题综合考察了三角形全等的判定和全等三角形的性质,根据不同的视角,可以考察不同的知识点,是一道不错的题目.
13. 如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
答案:A
解析:解答: ∵AC=AD
BC=BD(已知)
AB=AB
∴△ABC≌Rt△ABD(SSS)
∴∠CAB=∠DAB
∠CBA=∠DBA
∴选A.
分析:本题综合考察了三角形全等的判定和全等三角形的性质,是一道综合性很好的题目.
14.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
答案:C
解析:解答:由原题所给条件,可以得到有以下三对三角形全等
(1)△ABE≌△DCF
(2)△ABF≌△DCE
(3)△FBE≌△ECF
故有3对,选C.
分析:本题综合考察了三角形全等的多种判定方法,是一道综合性很好的题目.
15.已知:如图,点A,E,F,D在同一条直线上,AE=DF,AB=CD,BF⊥AD,CE⊥AD,垂足分别为F,E,则△ABF≌△DCE的依据是( )
A. SSS B. SAS C. ASA D. HL
答案:D
解析:解答:∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD
∴Rt△ABF≌Rt△DCE(HL)
分析:本题考查了全等三角形的判定方法中的HL判定定理.
二,填空题(共5题)
16.如图,MN与PQ相交于点O,MO=OP,QO=ON,∠M=65°,∠Q=30°,则∠P= ,∠N= .
答案:65°| 30°
解析:解答:∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对项角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
分析:本题考查了全等三角形的判定和全等三角形的性质,是一道综合性较好的题目.
17. 如图,已知AB=AC=12 cm,AE=AF=7 cm,CE=10 cm,△ABF的周长是 .
答案:29cm
解析:解答:∵AB=AC,AE=AF=7(已知),
∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长
=AB+BF+FA
=12+7+10
=29(cm)
分析:本题考查了全等三角形的判定和三角形周长的计算,是一道较好的题目.
18. 如图,已知BC=EC,∠BCE=∠ACD,要使能用SAS说明△ABC≌△DEC,则应添加的一个条件为______.(答案不唯一,只需填一个)
答案:AC=CD
解析:解答:∵∠BCE=∠ACD(已知),
∴∠BCE+∠ACE=∠ACE +∠ACD
∴∠BCA=∠ECD
∵BC=EC,AC=CD
∴△ABC≌△DEC(SAS)
分析:本题考查了全等三角形的判定和角的计算,是一道较好的题目.
19.如图 , 已知:AB=AC , D是BC边的中点 , 则∠1+∠C=_____度.
答案:90.
解析:解答:∵AB=AC , D是BC边的中点(已知),
∴∠B=∠C, AD⊥BC
∴∠1+∠B=90°
∴∠1+∠C=90度
分析:本题考查了等腰三角形的性质和角的计算,是一道较好的题目.
20.如图所示的方格中,连接AB,AC,则∠1+∠2=____ ____度.
答案:90.
解析:解答:∵由题知小方格边长相等(已知),
∴AC与AB所在的两个直角三角形全等
∵AC是其所在直角三角形的斜边
∴两个锐角互余
∴易得∠1+∠2=90度
分析:本题考查了全等三角形的判定方法SAS,以及数形结合,是一道较好的题目.
三,解答题(共5题)
21.(2014 常州)已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
答案:答案见解析
解析:解答:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS).
分析:本题考查了线段中点的性质以及全等三角形的判定方法,综合性比较强.
22.(2014 吉林)如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,
求证:△ABD≌△AEC.
答案:答案见解析
解析:解答:∵∠BAC=∠DAE,
∴∠BAC-BAE=∠DAE-∠BAE,
即∠BAD=∠CAE,
在△ABD和△AEC中,
∴△ABD≌△AEC(SAS).
分析:本题考查了角的和差计算以及全等三角形的判定方法,是一道综合性比较强的题目.需要在审题时细心研究,不急不躁.
23.已知:如图,AD是△ABC的高,E是AD上一点,BE的延长线交AC于点F,BE=AC,DE=DC,BE和AC垂直吗?说明理由.
答案:BE⊥AC.
解析:解答:在Rt△BDE和 Rt△ACD中,
∴Rt△BDE≌ Rt△ACD (HL).
∴∠BDE=∠CAD.
∵AD是△ABC的高,
∴∠CAD+∠C=90°.
∴∠BDE +∠C=90°.
∴∠BFD=90°.
∴BE⊥AC.
分析:本题考查了余角的性质,垂直的判定以及全等三角形的判定方法,是一道综合性比较强的题目.需要在审题时细心研究,不急不躁.
24.如图,已知AB=AC,E,D分别是AB,AC的中点,且AF⊥BD交BD的延长线于F,AG⊥CE交CE的延长线于G,试判断AF和AG的关系是否相等,并说明理由.
答案:AF=AG.
解析:解答:∵AB=AC,E,D分别是AB,AC的中点,
∴ AD=AE.
∴在△ABD和△ACE中,
∴△ABD≌△ACE (SAS).
∴∠ABD≌∠ACE.
在△ABF和△ACG中,
∴△ABF≌△ACG (AAS).
∴AF=AG.
分析:本题考查了线段中点的性质应用以及多种全等三角形的判定方法,是一道综合性比较强的题目.需要在审题时细心研究,不急不躁.
25. 如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
答案:BE=CF
解析:解答:∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴ DE=DF.
∴在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).
∴BE=CF.
分析:本题考查了角平线的性质和全等三角形的判定方法
第14题图
A
B
C
D
E
F
第15题图
C
B
F
E
A
第23题图
第24题图
第25题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com第 11 页 (共 12 页) 版权所有@21世纪教育网
北师大版数学七年级下册第四章4.3探索三角形全等的条件课后练习
一,选择题(共15题)
1. 如图,已知AB=AD,那么添加下列一个条件后,能用SAS判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
答案:B
解析:解答:∵AB=AD (已知),AC=AC(公共边)
∴只需要BAC=∠DAC
∴△ABE≌△ACD
故选B.
分析:本题考察了全等三角形的判定方法中的SAS,较为简单.
2.如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
A.∠B=∠C B.∠AEB=∠ADC C.AE=AD D.BE=DC
答案:C
解析:解答:∵AB=AC (已知),∠A=∠A(公共角)
∴只需要AE=AD
∴△ABE≌△ACD
故选C.
分析:本题考察了全等三角形的判定方法中的SAS,较为简单.
3. 如图,已知E,F是AC上的两点,AE=CF,DF=BE,∠AFD=∠CEB,则下列不成立的是( )
A.∠A=∠C B.AD=CB C.BC=DF D.DF∥BE
答案:C
解析:解答:∵AE=CF(已知),
∴AE+EF=EF+CF
∴AF=EC
∵∠AFD=∠CEB
∴△AFD≌△CEB(SAS)
∴∠A=∠C
AD=CB
BC=DA
∵∠AFD=∠CEB
∴DF∥BE
故选C.
分析:本题综合考察了三角形的多个知识点,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
4.如图,在△ABD中,AC⊥BD,点C是BD的中点,则下列结论错误的是( )
A.AB=AD B.AB=BD C. ∠B=∠D D.AC平分∠BAD
答案:B
解析:解答:∵AC⊥BD,点C是BD的中点
∴AB=AD(线段中垂线的性质)
∴∠B=∠D(等边对等角)
∴∠BAC=∠DAC(等腰三角形三线合一)
∴AC平分∠BAD
选B .
分析:本题综合考察了三角形的多个知识点,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
5.如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )
A.40° B.50° C.60° D.70°
答案:D
解析:解答:∵∠E=40°,∠F=70°
∴∠D =70°
∵FE=BC
DE=AB
∠B=∠E=40°
∴△ABC≌△DEF(SAS)
∴∠A=∠D =70°
选D .
分析:本题综合考察了三角形全等的判定,全等三角形的性质和三角形的内角和,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
6.在下列条件中,不能说明△ABC≌△A’B’C,,的是( )
A,∠A=∠A’,∠C=∠C’,AC=A’C’ B,∠A=∠A’,AB=A’B’,BC=B’C’
C,∠B=∠B’,∠C=∠C’,AB=A’B’ D,AB=A’B’, BC=B’ C’AC=A’C’
答案:B
解析:解答:对于B, 如果∠A=∠A’=90°,全等,但题目中没告诉是否为90°,故不一定全等.故选B .
分析:本题综合考察了三角形全等的判定,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
7.在下列说法中,正确的有( )个.
①三角对应相等的两个三角形全等;②三边对应相等的两个三角形全等;③两角,一边对应相等的两个三角形全等;④两边,一角对应相等的两个三角形全等.
A,1 B,2 C,3 D,4
答案:B
解析:解答:对于①,只能得到相似;对于②,运用SSS可以得到全等;对于③可以运用ASA或AAS判定全等;对于④,当SAS时全等,但当SSA时不一定全等.故选B .
分析:本题综合考察了三角形全等的判定,考察学生灵活运用所学知识处理问题的能力,是一道综合性很强的题目.
8.下列说法正确的是( )
A,两个周长相等的长方形全等 B,两个周长相等的三角形全等
C,两个面积相等的长方形全等 D,两个周长相等的圆全等
答案:D
解析:解答:对于两个图形,只有知道两个圆的半径相等,则这两个圆就全等,其余选项,皆不能得到全等,故选D .
分析:本题综合考察了全等图形的判定,结合了上一节内容,考察学生灵活处理问题的能力.
9. 使两个直角三角形全等的条件是( )
A. 一锐角对应相等 B. 两锐角对应相等
C. 一条边对应相等 D. 两条边对应相等
答案:D
解析:解答:对于两个直角三角形,已经知道有一组角对应相等了,因此,运用HL定理可以判定两个直角三角形全等,选D .
分析:本题综合考察了全等三角形的判定中的HL定理,内容简单.
10.如图,分别为的,边的中点,将此三角形沿折叠,使点落在边上的点处.若,则等于( )
A. B. C . D.
答案:B
解析:解答: 由翻折得△PDE≌△CDE
∴∠PDE=∠CDE=48°
∵分别为的,边的中点,
∴D E∥AB
∴∠APD=∠PDE=48°
∴选B.
分析:本题综合考察了全等三角形的性质,三角形的中位线定理和平行线的性质,考察知识点较多,是一道不错的题目.
11. 如图,△ABC≌△CDA,且AD=CB,下列结论错误的是( )
A,∠B=∠D B,∠CAB=∠ACD C,BC=CD D,AC=CA
答案:C
解析:解答: ∵△ABC≌△CDA,且AD=CB
∴∠B=∠D
∠CAB=∠ACD
AC=CA
∴选C.
分析:本题综合考察了全等三角形的性质,考察知识点较多,是一道不错的题目.
12.已知:如图,AC=CD ,∠B=∠E=90°, AC⊥CD,则不正确的结论是 ( )
A,∠A与∠D互为余角 B,∠A=∠2
C,△ABC≌△CED D,∠1=∠2
答案:D
解析:解答: ∵AC⊥CD
∴∠ACD=90°
∵∠1+∠2+∠ACD=180°
∴∠1+∠2=90°
∴选D.
分析:本题综合考察了三角形全等的判定和全等三角形的性质,根据不同的视角,可以考察不同的知识点,是一道不错的题目.
13. 如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD B.CD垂直平分AB
C.AB与CD互相垂直平分 D.CD平分∠ACB
答案:A
解析:解答: ∵AC=AD
BC=BD(已知)
AB=AB
∴△ABC≌Rt△ABD(SSS)
∴∠CAB=∠DAB
∠CBA=∠DBA
∴选A.
分析:本题综合考察了三角形全等的判定和全等三角形的性质,是一道综合性很好的题目.
14.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
A.1对 B.2对 C.3对 D.4对
答案:C
解析:解答:由原题所给条件,可以得到有以下三对三角形全等
(1)△ABE≌△DCF
(2)△ABF≌△DCE
(3)△FBE≌△ECF
故有3对,选C.
分析:本题综合考察了三角形全等的多种判定方法,是一道综合性很好的题目.
15.已知:如图,点A,E,F,D在同一条直线上,AE=DF,AB=CD,BF⊥AD,CE⊥AD,垂足分别为F,E,则△ABF≌△DCE的依据是( )
A. SSS B. SAS C. ASA D. HL
答案:D
解析:解答:∵AE=DF(已知),
∴AE+EF=EF+DF
∴AF=ED
∵AB=CD,BF⊥AD,CE⊥AD
∴Rt△ABF≌Rt△DCE(HL)
分析:本题考查了全等三角形的判定方法中的HL判定定理.
二,填空题(共5题)
16.如图,MN与PQ相交于点O,MO=OP,QO=ON,∠M=65°,∠Q=30°,则∠P= ,∠N= .
答案:65°| 30°
解析:解答:∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对项角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
分析:本题考查了全等三角形的判定和全等三角形的性质,是一道综合性较好的题目.
17. 如图,已知AB=AC=12 cm,AE=AF=7 cm,CE=10 cm,△ABF的周长是 .
答案:29cm
解析:解答:∵AB=AC,AE=AF=7(已知),
∠A=∠A(公共角)
∴△ABC≌△ACE(SAS)
∴BF=CE=10 cm,
∴△ABF的周长
=AB+BF+FA
=12+7+10
=29(cm)
分析:本题考查了全等三角形的判定和三角形周长的计算,是一道较好的题目.
18. 如图,已知BC=EC,∠BCE=∠ACD,要使能用SAS说明△ABC≌△DEC,则应添加的一个条件为______.(答案不唯一,只需填一个)
答案:AC=CD
解析:解答:∵∠BCE=∠ACD(已知),
∴∠BCE+∠ACE=∠ACE +∠ACD
∴∠BCA=∠ECD
∵BC=EC,AC=CD
∴△ABC≌△DEC(SAS)
分析:本题考查了全等三角形的判定和角的计算,是一道较好的题目.
19.如图 , 已知:AB=AC , D是BC边的中点 , 则∠1+∠C=_____度.
答案:90.
解析:解答:∵AB=AC , D是BC边的中点(已知),
∴∠B=∠C, AD⊥BC
∴∠1+∠B=90°
∴∠1+∠C=90度
分析:本题考查了等腰三角形的性质和角的计算,是一道较好的题目.
20.如图所示的方格中,连接AB,AC,则∠1+∠2=____ ____度.
答案:90.
解析:解答:∵由题知小方格边长相等(已知),
∴AC与AB所在的两个直角三角形全等
∵AC是其所在直角三角形的斜边
∴两个锐角互余
∴易得∠1+∠2=90度
分析:本题考查了全等三角形的判定方法SAS,以及数形结合,是一道较好的题目.
三,解答题(共5题)
21.(2014 常州)已知:如图,点C为AB中点,CD=BE,CD∥BE.
求证:△ACD≌△CBE.
答案:答案见解析
解析:解答:∵C是AB的中点(已知),
∴AC=CB(线段中点的定义).
∵CD∥BE(已知),
∴∠ACD=∠B(两直线平行,同位角相等).
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS).
分析:本题考查了线段中点的性质以及全等三角形的判定方法,综合性比较强.
22.(2014 吉林)如图,△ABC和△DAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,
求证:△ABD≌△AEC.
答案:答案见解析
解析:解答:∵∠BAC=∠DAE,
∴∠BAC-BAE=∠DAE-∠BAE,
即∠BAD=∠CAE,
在△ABD和△AEC中,
∴△ABD≌△AEC(SAS).
分析:本题考查了角的和差计算以及全等三角形的判定方法,是一道综合性比较强的题目.需要在审题时细心研究,不急不躁.
23.已知:如图,AD是△ABC的高,E是AD上一点,BE的延长线交AC于点F,BE=AC,DE=DC,BE和AC垂直吗?说明理由.
答案:BE⊥AC.
解析:解答:在Rt△BDE和 Rt△ACD中,
∴Rt△BDE≌ Rt△ACD (HL).
∴∠BDE=∠CAD.
∵AD是△ABC的高,
∴∠CAD+∠C=90°.
∴∠BDE +∠C=90°.
∴∠BFD=90°.
∴BE⊥AC.
分析:本题考查了余角的性质,垂直的判定以及全等三角形的判定方法,是一道综合性比较强的题目.需要在审题时细心研究,不急不躁.
24.如图,已知AB=AC,E,D分别是AB,AC的中点,且AF⊥BD交BD的延长线于F,AG⊥CE交CE的延长线于G,试判断AF和AG的关系是否相等,并说明理由.
答案:AF=AG.
解析:解答:∵AB=AC,E,D分别是AB,AC的中点,
∴ AD=AE.
∴在△ABD和△ACE中,
∴△ABD≌△ACE (SAS).
∴∠ABD≌∠ACE.
在△ABF和△ACG中,
∴△ABF≌△ACG (AAS).
∴AF=AG.
分析:本题考查了线段中点的性质应用以及多种全等三角形的判定方法,是一道综合性比较强的题目.需要在审题时细心研究,不急不躁.
25. 如图所示,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且BD=CD,那么BE与CF相等吗?为什么?
答案:BE=CF
解析:解答:∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴ DE=DF.
∴在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).
∴BE=CF.
分析:本题考查了角平线的性质和全等三角形的判定方法
第14题图
A
B
C
D
E
F
第15题图
C
B
F
E
A
第23题图
第24题图
第25题图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com第 11 页 (共 12 页) 版权所有@21世纪教育网
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
