北师大版数学七年级下册第五章5.4利用轴对称设计课时练习
文档属性
| 名称 | 北师大版数学七年级下册第五章5.4利用轴对称设计课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-17 11:17:26 | ||
图片预览

文档简介
登陆21世纪教育 助您教考全无忧
北师大版数学七年级下册第五章5.4利用轴对称设计课时练习
一、选择题(共15个小题)
1.两个图形关于某直线对称,对称点一定在( )
A.这直线的两旁 B.这直线的同旁 C.这直线上 D.这直线两旁或这直线上
答案:D
解析:解答:根据轴对称的性质可以直接得到选D.
分析:本题关键是正确理解成轴对称图形的性质,属于直接考察对课本内容的理解.
2.对于下列命题:①一直线成轴对称的两个三角形全等;②等腰三角形的对称轴是顶角的平分线;③一条线段的两个端点一定是关于经过该线段中点的直线的对称点;④如果两个三角形全等,那么它们关于某直线成轴对称.其中真命题的个数为( )
A.0 B.1 C.2 D.3
答案:B
解析:解答:四个命题中,①关于某一直线成轴对称的两个三角形全等正确,是由轴对称的性质得到的;②错误,应该是顶角的平分线所在的直线;③错误,经过线段的中点的直线不一定和这条线段垂直;④错误,成轴对称一定全等,但全等不一定成轴对称.故有1个真.
故选B
分析:本题关键是在细节处注意正确与错误.特别是关于对称轴的叙述,必须是直线.
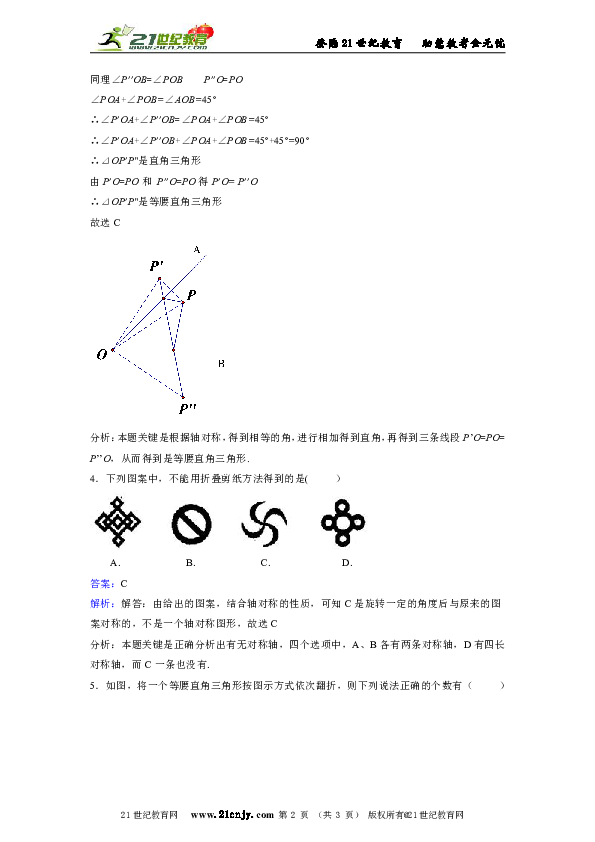
3.已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )
A.直角三角形 B.钝角三角形 C.等腰直角三角形 D.等边三角形
答案:C
解析:解答:如下图所示,连结P’O、PO、P’’O
∵P′与P关于OA对称
∴∠P’OA=∠POA P’O=PO
同理∠P’’OB=∠POB P’’O=PO
∠POA+∠POB=∠AOB=45°
∴∠P’OA+∠P’’OB=∠POA+∠POB=45°
∴∠P’OA+∠P’’OB+∠POA+∠POB=45°+45°=90°
∴⊿OP’P"是直角三角形
由P’O=PO和 P’’O=PO得P’O= P’’O
∴⊿OP’P"是等腰直角三角形
故选C
分析:本题关键是根据轴对称,得到相等的角,进行相加得到直角,再得到三条线段P’O=PO= P’’O,从而得到是等腰直角三角形.
4.下列图案中,不能用折叠剪纸方法得到的是( )
A. B. C. D.
答案:C
解析:解答:由给出的图案,结合轴对称的性质,可知C是旋转一定的角度后与原来的图案对称的,不是一个轴对称图形,故选C
分析:本题关键是正确分析出有无对称轴,四个选项中,A、B各有两条对称轴,D有四长对称轴,而C一条也没有.
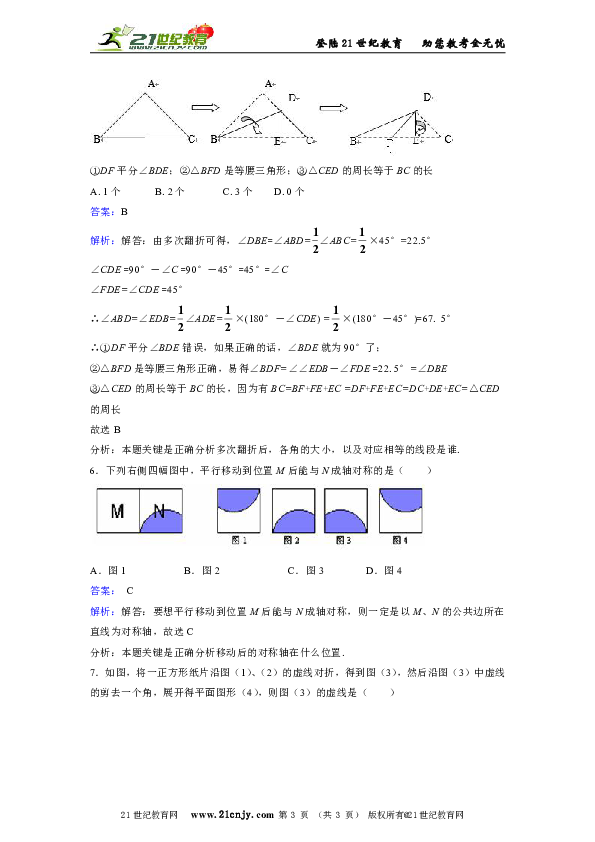
5.如图,将一个等腰直角三角形按图示方式依次翻折,则下列说法正确的个数有( )
①DF平分∠BDE;②△BFD是等腰三角形;③△CED的周长等于BC的长
A.1个 B.2个 C.3个 D.0个
答案:B
解析:解答:由多次翻折可得,∠DBE=∠ABD=∠ABC=×45°=22.5°
∠CDE =90°-∠C =90°-45°=45°=∠C
∠FDE=∠CDE =45°
∴∠ABD=∠EDB=∠ADE=×(180°-∠CDE) =×(180°-45°)=67. 5°
∴①DF平分∠BDE错误,如果正确的话,∠BDE就为90°了;
②△BFD是等腰三角形正确,易得∠BDF=∠∠EDB-∠FDE =22.5°=∠DBE
③△CED的周长等于BC的长,因为有BC=BF+FE+EC =DF+FE+EC=DC+DE+EC=△CED的周长
故选B
分析:本题关键是正确分析多次翻折后,各角的大小,以及对应相等的线段是谁.
6.下列右侧四幅图中,平行移动到位置M后能与N成轴对称的是( )
A.图1 B.图2 C.图3 D.图4
答案: C
解析:解答:要想平行移动到位置M后能与N成轴对称,则一定是以M、N的公共边所在直线为对称轴,故选C
分析:本题关键是正确分析移动后的对称轴在什么位置.
7.如图,将一正方形纸片沿图(1)、(2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )
答案:D
解析:解答:要想得到平面图形(4),需要注意(4)中内部的矩形与原来的正方形纸片的边平行.故剪时,虚线也与正方形纸片的边平行,故选D
分析:本题关键是正确分析出所剪时的虚线与正方形纸片的边平行.
8.桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A,则如图所示8个点中,可以瞄准的点的个数( )
A.1 B.2 C.4 D.6
答案: B
解析:解答:要想一次反弹后击中A,需要入射角也反射角相等,因此,可以经过如下图所示的两条路径达到要求,即B-D-A或者B-C-A,另外的一次反弹路线,都不经过图中给出的点,故选B.
分析:本题关键是正确理解分析出反弹角度与B碰撞边的角度相同.
9.下列命题中,正确的是( )
A.两个全等的三角形合在一起是一个轴对称图形
B.等腰三角形的对称轴是底边上的中线
C.等腰三角形底边上的高就是底边的垂直平分线
D.一条线段可以看做以它的垂直平分线为对称轴的轴对称图形
答案:D
解析:解答:对于四个选项,A两个全等三角形合在一起不一定是轴对称图形,需要看实际组合成什么样的图形;B中应该为底边上的中线所在的直线;C应该是底边的垂直平分线被三角形所截取的线段;故此题正确选项为D.
分析:本题关键是正确理解轴对称图形的特点,对称轴是直线.
10.下列说法中,正确的是( )
A.两个全等三角形,一定是轴对称的
B.两个轴对称的三角形,一定是全等的
C.三角形的一条中线把三角形分成以中线为轴对称的两个图形
D.三角形的一条高把三角形分成以高线为轴对称的两个图形
答案:B
解析:解答:对于四个选项,A两个全等三角形,一定是轴对称的.错误,全等不一定对称,但对称一定全等,所以A错,B对.故应选B.
分析:本题关键是正确理解成轴对称的两个图形的特点.
11.在直线、线段、角、两条平行直线组成的图形、两条相交直线组成的图形这些图形中,是轴对称图形的有( )
A.5个 B.4个 C.3个 D.2个
答案:A
解析:解答:由轴对称的性质得,直线是轴对称图形,线段是有两条对称轴的轴对称图形,角的对称轴是其角平分线所在的直线;两条平行直线也是轴对称图形,两条相交直线也是轴对称图形,都是轴对称图形,故有5个.应选A.
分析:本题关键是正确判断经出的图形,是否符合轴对称图形的特点.
12.如图△ABC和△A'B'C'关于直线l对称,下列结论中:①△ABC△A'B'C';②∠BAC'=∠B'AC;③l垂直平分CC';④直线BC和B'C',的交点不一定在l上.正确的有( )
A.4个 B.3个 C.2个 D.1个
答案:B
解析:解答:由轴对称的性质得,轴对称的两个图形全等,故①正确;由全等三角形的对应角相等得到∠BAC'=∠B'AC,故②正确;因为轴对称图形的对应点的连线被对称轴垂直平分,故③正确;因为轴对称图形对应线段平行或交点在对称轴上,而由图知BC和B'C'不平行,所以交点一定在l。综上所述,前三个正确,故选A.
分析:本题关键是正确分析轴对称的两个图形有什么特点.
13.如图,△ABC与△A’B’C’关于直线MN对称,P为MN上任一点,下列错误的是( )
A.△AA’P是等腰三角形 B.MN垂直平分AA’,CC’
C.△ABC与△A’B’C’面积相等 D.直线AB、A’B的交点不一定在MN上
答案:D
解析:解答:由轴对称的性质得,直线MN是线段AA’ 、CC’的对称轴,又P在直线MN上,所以A中的△AA’P是等腰三角形是正确的;B中 MN垂直平分AA’,CC’也是正确的;因为轴对称的两个图形全等,全等图形的面积当然相等,故C也是正确的.用排除法,可以判定选D.
分析:本题关键是正确分析轴对称的两个图形有什么特点.
14.若一个三角形是轴对称图形,则这个三角形一定是( )
A.等边三角形 B.不等边三角形 C.等腰三角形 D.等腰直角三角形
答案:C
解析:解答:A等边三角形一定是轴对称图形,但轴对称三角形不一定是等边三角形;B不等边三角形一定不是轴对称图形;C等腰三角形一定是轴对称三角形;D等腰直角三角形一定是轴对称图形,但是轴对称三角形不一定是等腰直角三角形.故选C.
分析:本题关键是正确分析轴对称的三角形有什么特点.
15.下列说法正确的有( )个
①有一个外角是120°的等腰三角形是等边三角形.
②有两个外角相等的等腰三角形是等边三角形.
③有一边上的高也是这边上的中线的等腰三角形是等边三角形.
④三个外角都相等的三角形是等边三角形.
A.4个 B.3个 C.2个 D.1个
答案:C
解析:解答:①有一个外角是120°则其相邻的内角为60°,又是等腰三角形,所以必定是等边三角形,正确;②有两个外角相等,则与这两个外角相邻的内角也相等,但是如果这两个内角就是原来等腰三角形的两个底角,则不能判定是等边三角形;故错误;③有一边上的高也是这边上的中线,如果这条边恰好是原等腰三角形的底边,则不能判定这个等腰三角形是等边三角形;故错误;④三个外角都相等,则三个内角也相等,当然是等边三角形,正确;综上有两个正确.故选C.
分析:本题关键是正确分析是等腰三角形的顶角还是底角.
二、填空题(共5个小题)
16.如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P’、P’’,连P’P’’交OA于点M,交OB于点N,若P’P’’=5cm,则△PMN的周长为 .
答案:5cm
解析:解答:由轴对称可知,MP =MP’ NP =NP’
∵P’P’’ =5cm
∴P’P’’ = P’M +MN + NP’’ =5cm
∴PM +MN + NP = P’M +MN + NP’’ = 5cm
∴△PMN的周长为5cm
分析:本题关键是根据对称把三角形的三条边转化到一条线段上,再根据已知就容易得到结果了.
17.如图,矩形ABCD中将其沿EF翻折后,D点恰落在B处,∠BFE= 650,则∠AEB= .
答案:50°
解析:解答:如下图由矩形ABCD可得AD∥BC
∴∠1=∠BFE =65°
由翻折得∠2=∠1 =65°
∴∠AEB =180°-∠1- ∠2 =180°-65°-65°=50°
分析:本题关键是根据翻折求出各个角的度数,再根据平角180°求出∠AEB的度数.
18.如图,△ABC中,∠ A=500,∠C=700,BD、BE三等分∠ABC,将△BCE沿BE对折,点C落在C’处,则∠1= ;
答案:90°
解析:解答:∵∠ A=500,∠C=700
∴∠ABC =60°
∵BD、BE三等分∠ABC
∴∠ABE =∠EBD =∠DBC =20°
∴∠EBC =∠EBD +∠DBC =40°
由翻折得∠C’BE=∠EBC =40° ∠C’ =∠C =70°
∠C’BA =∠C’BE-∠ABE =40°-20°=20°
∵三角形的一个外角等于和它不相邻的两个内角的和
∴∠1=∠C’ +∠C’BA =70°+20°=90°
分析:本题关键是根据翻折求出各个角的度数,再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1的度数.
19.如图,△ABE和△ADC是△ABC分别沿AB、AC边翻折得到的,若∠1: ∠2:∠3 = 28 :5 : 3, 则∠4的度数为
答案:80°
解析:解答:∵∠1: ∠2:∠3 = 28 :5 : 3
∠1+∠2+∠3 = 180°
∴∠1=140° ∠2=25° ∠3=15°
由翻折得∠EBA =∠2 =25° ∠DCA =∠3 =15°
∴∠EBC=∠EBA +∠2 =50° ∠DCB =∠DCA +∠3 =30°
∵三角形的一个外角等于和它不相邻的两个内角的和
∴∠4=∠EBC +∠DCB =50°+30°=80°
分析:本题关键是根据翻折求出各个角的度数,再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠4的度数.
20.如图△ABC中,AB=BC,∠A=36°,BD平分∠ABC交AC于D,则图中的等腰三角形有 个
答案:3
解析:解答:∵在△ABC中,AB=BC,∠A=36°
∴∠ABC=∠ACB =72°
∵BD平分∠ABC
∴∠ABD=∠CBD =36°
∴∠ABD=∠A =36° ∠BDC =72°=∠C
∴△ABD和△BDC都是等腰三角形
故有三个等腰三角形 故有三个.
分析:本题关键是根据条件求出各个角的度数,由此确定哪个三角形是等腰三角形
三、解答题(共5个小题)
21. 画出所示⊿关于直线l对称的⊿(保留痕迹)
答案:
解答:作⊿的步骤如下:
1作点⊿的三个顶点A、B、C关于直线l对称的点A’、B’、C’;
2顺次连结A’B’、 B’ C’、C’ A’得⊿A’B’C.
则⊿A’B’C即为所求作的三角形.
解析:
分析:本题关键是确定以哪条直线为对称轴,然后在确定两色磁砖的摆放位置.
22.用四块如图所示的两色正方形瓷砖,拼成一个新的正方形,使拼成轴对称图案,请至少给出三种不同的拼法:
答案:根据轴对称要求,设计出利用两色磁砖拼成的正方形如上图所示.
解析:解答: 见答案
分析:本题关键是确定以哪条直线为对称轴,然后在确定两色磁砖的摆放位置.
23.请你应用轴对称的知识画出图中的图形,并涂上彩色,与同学比一比,看谁画得正确、漂亮.
答案:关于画给出的图形步骤如下:
1作一个正方形ABCD;
2分别以正方形ABCD的四条边为直径,作四个圆;
3以这四个圆的公共点为圆心O,OA长为半径作一个圆.
4将线段与字母去掉.
就得到上图第二个图形.
涂色根据轴对称要求,提供一例如右上图示.
根据题意,以下图为示例:
解析:解答:见答案
分析:本题中多次运用轴对称,关键是找出各个圆的圆心位置.
24.将△ABC的∠C折起,翻折后角的顶点位置记作C′,当C′落在AC上时(如图1),易证:∠1=2∠2.
当C′点落在CA和CB之间(如图2)时,或当C′落在CB、CA的同旁(如图3)时,∠1、∠2、∠3关系又如何?请写出你的猜想,并就其中一种情况给出证明.
图1 图2 图3
答案:当C′点落在CA和CB之间(如图2)时,∠1+∠3=2∠2;
当C′落在CB、CA的同旁(如图3)时,∠1-∠3=2∠2;
对于图2,连结CC’,如图4所示,
∵⊿EC’D是由⊿ECD翻折得到的
∴⊿EC’D≌⊿ECD,由此得EC=EC’,DC=DC’, ∠EC’D=∠ECD
∴∠EC’C=∠ECC;∠DC’C=∠DCC
∵∠1=∠DC’C+∠DCC’ ∠3=∠EC’C+∠ECC’
∴∠1+∠3=∠DC’C+∠DCC’ +∠ EC’C+∠ECC’=2∠DC’C+2∠ EC’C =2(∠DC’C+∠ EC’C)= 2∠2;
∴∠1+∠3=2∠2
对于图3,设AC与DC’在⊿ABC内部所夹角为∠4,如图5所示,则有
∠1=∠C+∠4,∠4=∠3+∠2
又由翻折得:∠2=∠C
∴∠1=∠2+∠3+∠2=∠3+2∠2
∴∠1-∠3=2∠2
解析:解答:具体过程见答案。
分析:本题中多次运用轴对称,关键是要考虑到原先给出的两条直线并不是全部的对称轴,这是最主要的.
25.如图所示,两条相交直线l1与l2的夹角是45°,都是一个图案的对称轴,画出这个图案的其余部分,这个图案共有多少条对称轴
答案:
∵直线l1与l2的夹角是45°,都是一个图案的对称轴
∴首先以l1为对称轴,作出第一次轴对称的图形;得到的图案是右上角占全图四分之一的部分;此时出现了第三条对称轴;
第二,再以 l2为对称轴,作出第二次轴对称的图形;得到的图案是整个图案的一半;此时出现了第四条对称轴;
第三,以第三条对称轴为对称轴,作出整个图案,如上图.
解析:解答:具体过程见答案.
分析:本题中多次运用轴对称,关键是要考虑到原先给出的两条直线并不是全部的对称轴,这是最主要的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com第 13 页 (共 13 页) 版权所有@21世纪教育网
北师大版数学七年级下册第五章5.4利用轴对称设计课时练习
一、选择题(共15个小题)
1.两个图形关于某直线对称,对称点一定在( )
A.这直线的两旁 B.这直线的同旁 C.这直线上 D.这直线两旁或这直线上
答案:D
解析:解答:根据轴对称的性质可以直接得到选D.
分析:本题关键是正确理解成轴对称图形的性质,属于直接考察对课本内容的理解.
2.对于下列命题:①一直线成轴对称的两个三角形全等;②等腰三角形的对称轴是顶角的平分线;③一条线段的两个端点一定是关于经过该线段中点的直线的对称点;④如果两个三角形全等,那么它们关于某直线成轴对称.其中真命题的个数为( )
A.0 B.1 C.2 D.3
答案:B
解析:解答:四个命题中,①关于某一直线成轴对称的两个三角形全等正确,是由轴对称的性质得到的;②错误,应该是顶角的平分线所在的直线;③错误,经过线段的中点的直线不一定和这条线段垂直;④错误,成轴对称一定全等,但全等不一定成轴对称.故有1个真.
故选B
分析:本题关键是在细节处注意正确与错误.特别是关于对称轴的叙述,必须是直线.
3.已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )
A.直角三角形 B.钝角三角形 C.等腰直角三角形 D.等边三角形
答案:C
解析:解答:如下图所示,连结P’O、PO、P’’O
∵P′与P关于OA对称
∴∠P’OA=∠POA P’O=PO
同理∠P’’OB=∠POB P’’O=PO
∠POA+∠POB=∠AOB=45°
∴∠P’OA+∠P’’OB=∠POA+∠POB=45°
∴∠P’OA+∠P’’OB+∠POA+∠POB=45°+45°=90°
∴⊿OP’P"是直角三角形
由P’O=PO和 P’’O=PO得P’O= P’’O
∴⊿OP’P"是等腰直角三角形
故选C
分析:本题关键是根据轴对称,得到相等的角,进行相加得到直角,再得到三条线段P’O=PO= P’’O,从而得到是等腰直角三角形.
4.下列图案中,不能用折叠剪纸方法得到的是( )
A. B. C. D.
答案:C
解析:解答:由给出的图案,结合轴对称的性质,可知C是旋转一定的角度后与原来的图案对称的,不是一个轴对称图形,故选C
分析:本题关键是正确分析出有无对称轴,四个选项中,A、B各有两条对称轴,D有四长对称轴,而C一条也没有.
5.如图,将一个等腰直角三角形按图示方式依次翻折,则下列说法正确的个数有( )
①DF平分∠BDE;②△BFD是等腰三角形;③△CED的周长等于BC的长
A.1个 B.2个 C.3个 D.0个
答案:B
解析:解答:由多次翻折可得,∠DBE=∠ABD=∠ABC=×45°=22.5°
∠CDE =90°-∠C =90°-45°=45°=∠C
∠FDE=∠CDE =45°
∴∠ABD=∠EDB=∠ADE=×(180°-∠CDE) =×(180°-45°)=67. 5°
∴①DF平分∠BDE错误,如果正确的话,∠BDE就为90°了;
②△BFD是等腰三角形正确,易得∠BDF=∠∠EDB-∠FDE =22.5°=∠DBE
③△CED的周长等于BC的长,因为有BC=BF+FE+EC =DF+FE+EC=DC+DE+EC=△CED的周长
故选B
分析:本题关键是正确分析多次翻折后,各角的大小,以及对应相等的线段是谁.
6.下列右侧四幅图中,平行移动到位置M后能与N成轴对称的是( )
A.图1 B.图2 C.图3 D.图4
答案: C
解析:解答:要想平行移动到位置M后能与N成轴对称,则一定是以M、N的公共边所在直线为对称轴,故选C
分析:本题关键是正确分析移动后的对称轴在什么位置.
7.如图,将一正方形纸片沿图(1)、(2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )
答案:D
解析:解答:要想得到平面图形(4),需要注意(4)中内部的矩形与原来的正方形纸片的边平行.故剪时,虚线也与正方形纸片的边平行,故选D
分析:本题关键是正确分析出所剪时的虚线与正方形纸片的边平行.
8.桌面上有A、B两球,若要将B球射向桌面任意一边,使一次反弹后击中A,则如图所示8个点中,可以瞄准的点的个数( )
A.1 B.2 C.4 D.6
答案: B
解析:解答:要想一次反弹后击中A,需要入射角也反射角相等,因此,可以经过如下图所示的两条路径达到要求,即B-D-A或者B-C-A,另外的一次反弹路线,都不经过图中给出的点,故选B.
分析:本题关键是正确理解分析出反弹角度与B碰撞边的角度相同.
9.下列命题中,正确的是( )
A.两个全等的三角形合在一起是一个轴对称图形
B.等腰三角形的对称轴是底边上的中线
C.等腰三角形底边上的高就是底边的垂直平分线
D.一条线段可以看做以它的垂直平分线为对称轴的轴对称图形
答案:D
解析:解答:对于四个选项,A两个全等三角形合在一起不一定是轴对称图形,需要看实际组合成什么样的图形;B中应该为底边上的中线所在的直线;C应该是底边的垂直平分线被三角形所截取的线段;故此题正确选项为D.
分析:本题关键是正确理解轴对称图形的特点,对称轴是直线.
10.下列说法中,正确的是( )
A.两个全等三角形,一定是轴对称的
B.两个轴对称的三角形,一定是全等的
C.三角形的一条中线把三角形分成以中线为轴对称的两个图形
D.三角形的一条高把三角形分成以高线为轴对称的两个图形
答案:B
解析:解答:对于四个选项,A两个全等三角形,一定是轴对称的.错误,全等不一定对称,但对称一定全等,所以A错,B对.故应选B.
分析:本题关键是正确理解成轴对称的两个图形的特点.
11.在直线、线段、角、两条平行直线组成的图形、两条相交直线组成的图形这些图形中,是轴对称图形的有( )
A.5个 B.4个 C.3个 D.2个
答案:A
解析:解答:由轴对称的性质得,直线是轴对称图形,线段是有两条对称轴的轴对称图形,角的对称轴是其角平分线所在的直线;两条平行直线也是轴对称图形,两条相交直线也是轴对称图形,都是轴对称图形,故有5个.应选A.
分析:本题关键是正确判断经出的图形,是否符合轴对称图形的特点.
12.如图△ABC和△A'B'C'关于直线l对称,下列结论中:①△ABC△A'B'C';②∠BAC'=∠B'AC;③l垂直平分CC';④直线BC和B'C',的交点不一定在l上.正确的有( )
A.4个 B.3个 C.2个 D.1个
答案:B
解析:解答:由轴对称的性质得,轴对称的两个图形全等,故①正确;由全等三角形的对应角相等得到∠BAC'=∠B'AC,故②正确;因为轴对称图形的对应点的连线被对称轴垂直平分,故③正确;因为轴对称图形对应线段平行或交点在对称轴上,而由图知BC和B'C'不平行,所以交点一定在l。综上所述,前三个正确,故选A.
分析:本题关键是正确分析轴对称的两个图形有什么特点.
13.如图,△ABC与△A’B’C’关于直线MN对称,P为MN上任一点,下列错误的是( )
A.△AA’P是等腰三角形 B.MN垂直平分AA’,CC’
C.△ABC与△A’B’C’面积相等 D.直线AB、A’B的交点不一定在MN上
答案:D
解析:解答:由轴对称的性质得,直线MN是线段AA’ 、CC’的对称轴,又P在直线MN上,所以A中的△AA’P是等腰三角形是正确的;B中 MN垂直平分AA’,CC’也是正确的;因为轴对称的两个图形全等,全等图形的面积当然相等,故C也是正确的.用排除法,可以判定选D.
分析:本题关键是正确分析轴对称的两个图形有什么特点.
14.若一个三角形是轴对称图形,则这个三角形一定是( )
A.等边三角形 B.不等边三角形 C.等腰三角形 D.等腰直角三角形
答案:C
解析:解答:A等边三角形一定是轴对称图形,但轴对称三角形不一定是等边三角形;B不等边三角形一定不是轴对称图形;C等腰三角形一定是轴对称三角形;D等腰直角三角形一定是轴对称图形,但是轴对称三角形不一定是等腰直角三角形.故选C.
分析:本题关键是正确分析轴对称的三角形有什么特点.
15.下列说法正确的有( )个
①有一个外角是120°的等腰三角形是等边三角形.
②有两个外角相等的等腰三角形是等边三角形.
③有一边上的高也是这边上的中线的等腰三角形是等边三角形.
④三个外角都相等的三角形是等边三角形.
A.4个 B.3个 C.2个 D.1个
答案:C
解析:解答:①有一个外角是120°则其相邻的内角为60°,又是等腰三角形,所以必定是等边三角形,正确;②有两个外角相等,则与这两个外角相邻的内角也相等,但是如果这两个内角就是原来等腰三角形的两个底角,则不能判定是等边三角形;故错误;③有一边上的高也是这边上的中线,如果这条边恰好是原等腰三角形的底边,则不能判定这个等腰三角形是等边三角形;故错误;④三个外角都相等,则三个内角也相等,当然是等边三角形,正确;综上有两个正确.故选C.
分析:本题关键是正确分析是等腰三角形的顶角还是底角.
二、填空题(共5个小题)
16.如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P’、P’’,连P’P’’交OA于点M,交OB于点N,若P’P’’=5cm,则△PMN的周长为 .
答案:5cm
解析:解答:由轴对称可知,MP =MP’ NP =NP’
∵P’P’’ =5cm
∴P’P’’ = P’M +MN + NP’’ =5cm
∴PM +MN + NP = P’M +MN + NP’’ = 5cm
∴△PMN的周长为5cm
分析:本题关键是根据对称把三角形的三条边转化到一条线段上,再根据已知就容易得到结果了.
17.如图,矩形ABCD中将其沿EF翻折后,D点恰落在B处,∠BFE= 650,则∠AEB= .
答案:50°
解析:解答:如下图由矩形ABCD可得AD∥BC
∴∠1=∠BFE =65°
由翻折得∠2=∠1 =65°
∴∠AEB =180°-∠1- ∠2 =180°-65°-65°=50°
分析:本题关键是根据翻折求出各个角的度数,再根据平角180°求出∠AEB的度数.
18.如图,△ABC中,∠ A=500,∠C=700,BD、BE三等分∠ABC,将△BCE沿BE对折,点C落在C’处,则∠1= ;
答案:90°
解析:解答:∵∠ A=500,∠C=700
∴∠ABC =60°
∵BD、BE三等分∠ABC
∴∠ABE =∠EBD =∠DBC =20°
∴∠EBC =∠EBD +∠DBC =40°
由翻折得∠C’BE=∠EBC =40° ∠C’ =∠C =70°
∠C’BA =∠C’BE-∠ABE =40°-20°=20°
∵三角形的一个外角等于和它不相邻的两个内角的和
∴∠1=∠C’ +∠C’BA =70°+20°=90°
分析:本题关键是根据翻折求出各个角的度数,再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠1的度数.
19.如图,△ABE和△ADC是△ABC分别沿AB、AC边翻折得到的,若∠1: ∠2:∠3 = 28 :5 : 3, 则∠4的度数为
答案:80°
解析:解答:∵∠1: ∠2:∠3 = 28 :5 : 3
∠1+∠2+∠3 = 180°
∴∠1=140° ∠2=25° ∠3=15°
由翻折得∠EBA =∠2 =25° ∠DCA =∠3 =15°
∴∠EBC=∠EBA +∠2 =50° ∠DCB =∠DCA +∠3 =30°
∵三角形的一个外角等于和它不相邻的两个内角的和
∴∠4=∠EBC +∠DCB =50°+30°=80°
分析:本题关键是根据翻折求出各个角的度数,再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠4的度数.
20.如图△ABC中,AB=BC,∠A=36°,BD平分∠ABC交AC于D,则图中的等腰三角形有 个
答案:3
解析:解答:∵在△ABC中,AB=BC,∠A=36°
∴∠ABC=∠ACB =72°
∵BD平分∠ABC
∴∠ABD=∠CBD =36°
∴∠ABD=∠A =36° ∠BDC =72°=∠C
∴△ABD和△BDC都是等腰三角形
故有三个等腰三角形 故有三个.
分析:本题关键是根据条件求出各个角的度数,由此确定哪个三角形是等腰三角形
三、解答题(共5个小题)
21. 画出所示⊿关于直线l对称的⊿(保留痕迹)
答案:
解答:作⊿的步骤如下:
1作点⊿的三个顶点A、B、C关于直线l对称的点A’、B’、C’;
2顺次连结A’B’、 B’ C’、C’ A’得⊿A’B’C.
则⊿A’B’C即为所求作的三角形.
解析:
分析:本题关键是确定以哪条直线为对称轴,然后在确定两色磁砖的摆放位置.
22.用四块如图所示的两色正方形瓷砖,拼成一个新的正方形,使拼成轴对称图案,请至少给出三种不同的拼法:
答案:根据轴对称要求,设计出利用两色磁砖拼成的正方形如上图所示.
解析:解答: 见答案
分析:本题关键是确定以哪条直线为对称轴,然后在确定两色磁砖的摆放位置.
23.请你应用轴对称的知识画出图中的图形,并涂上彩色,与同学比一比,看谁画得正确、漂亮.
答案:关于画给出的图形步骤如下:
1作一个正方形ABCD;
2分别以正方形ABCD的四条边为直径,作四个圆;
3以这四个圆的公共点为圆心O,OA长为半径作一个圆.
4将线段与字母去掉.
就得到上图第二个图形.
涂色根据轴对称要求,提供一例如右上图示.
根据题意,以下图为示例:
解析:解答:见答案
分析:本题中多次运用轴对称,关键是找出各个圆的圆心位置.
24.将△ABC的∠C折起,翻折后角的顶点位置记作C′,当C′落在AC上时(如图1),易证:∠1=2∠2.
当C′点落在CA和CB之间(如图2)时,或当C′落在CB、CA的同旁(如图3)时,∠1、∠2、∠3关系又如何?请写出你的猜想,并就其中一种情况给出证明.
图1 图2 图3
答案:当C′点落在CA和CB之间(如图2)时,∠1+∠3=2∠2;
当C′落在CB、CA的同旁(如图3)时,∠1-∠3=2∠2;
对于图2,连结CC’,如图4所示,
∵⊿EC’D是由⊿ECD翻折得到的
∴⊿EC’D≌⊿ECD,由此得EC=EC’,DC=DC’, ∠EC’D=∠ECD
∴∠EC’C=∠ECC;∠DC’C=∠DCC
∵∠1=∠DC’C+∠DCC’ ∠3=∠EC’C+∠ECC’
∴∠1+∠3=∠DC’C+∠DCC’ +∠ EC’C+∠ECC’=2∠DC’C+2∠ EC’C =2(∠DC’C+∠ EC’C)= 2∠2;
∴∠1+∠3=2∠2
对于图3,设AC与DC’在⊿ABC内部所夹角为∠4,如图5所示,则有
∠1=∠C+∠4,∠4=∠3+∠2
又由翻折得:∠2=∠C
∴∠1=∠2+∠3+∠2=∠3+2∠2
∴∠1-∠3=2∠2
解析:解答:具体过程见答案。
分析:本题中多次运用轴对称,关键是要考虑到原先给出的两条直线并不是全部的对称轴,这是最主要的.
25.如图所示,两条相交直线l1与l2的夹角是45°,都是一个图案的对称轴,画出这个图案的其余部分,这个图案共有多少条对称轴
答案:
∵直线l1与l2的夹角是45°,都是一个图案的对称轴
∴首先以l1为对称轴,作出第一次轴对称的图形;得到的图案是右上角占全图四分之一的部分;此时出现了第三条对称轴;
第二,再以 l2为对称轴,作出第二次轴对称的图形;得到的图案是整个图案的一半;此时出现了第四条对称轴;
第三,以第三条对称轴为对称轴,作出整个图案,如上图.
解析:解答:具体过程见答案.
分析:本题中多次运用轴对称,关键是要考虑到原先给出的两条直线并不是全部的对称轴,这是最主要的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com第 13 页 (共 13 页) 版权所有@21世纪教育网
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
