沪科版(2024)七年级数学下册 9.2.2 第1课时 分式的通分 课件 (共23张PPT)
文档属性
| 名称 | 沪科版(2024)七年级数学下册 9.2.2 第1课时 分式的通分 课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 662.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 19:59:59 | ||
图片预览







文档简介
(共23张PPT)
9.2.2 分式的加减
第一课时 分式的通分
学习目标及重难点
1.理解并掌握最简公分母的概念,能够求出几个分式的最简公分母;(重点)
2.能够对几个分式进行通分,并运用其解决问题.(难点)
算一算:
复习回顾
同分母分数相加减
算一算:
异分母分数相加减
分数的通分
依据:分数的基本性质
同分母分数相加减
关键:确定公分母
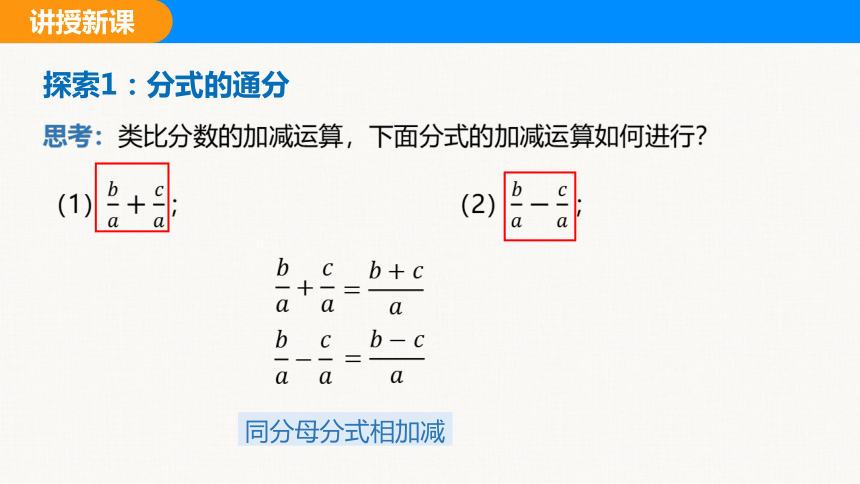
探索1:分式的通分
思考:类比分数的加减运算,下面分式的加减运算如何进行?
(1) ; (2) ;
同分母分式相加减
同分母分式相加减
思考:类比分数的加减运算,下面分式的加减运算如何进行?
(3) (4)
异分母分式相加减
分式的通分
依据:分式的基本性质
同分母分式相加减
关键:确定公分母
与分数类似,在计算异分母分式的加减时,要利用分式的基本性质,先把分母不相同的分式化成分母相同的分式,再进行加减.化异分母的分式为同分母的分式的过程,叫作分式的通分.
异分母分式通分时,关键是确定公分母.通常取各分母所有因式的最高次幂的积作为公分母,这样的公分母叫作最简公分母.
归纳总结
思考:怎么找分式的最简公分母?
观察并找出下面各组分式最简公分母:
一定系数:取各分母系数的最小公倍数;
二定因式:取各分母中出现的所有字母;
三定指数:取分母中相同字母的最高次幂.
(1)与
最简公分母:
最简公分母:
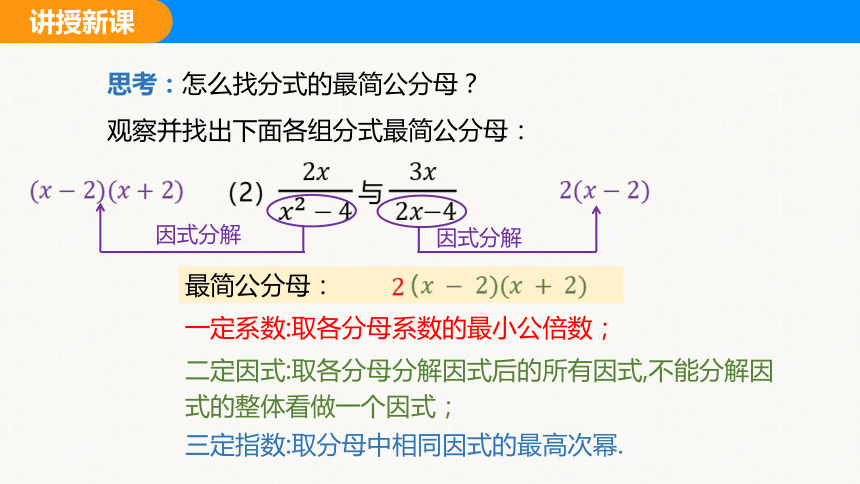
思考:怎么找分式的最简公分母?
观察并找出下面各组分式最简公分母:
一定系数:取各分母系数的最小公倍数;
二定因式:取各分母分解因式后的所有因式,不能分解因式的整体看做一个因式;
三定指数:取分母中相同因式的最高次幂.
(2) 与
因式分解
因式分解
怎样确定最简公分母呢?
(1)一定系数 : 取各分母系数的最小公倍数;
(2)二定因式 : 单项式:取各分母的所有字母.
多项式:取各分母分解因式后的所有因式,不能分解因式
的整体看做一个因式;(分母是多项式:先分解因式)
(3)三定指数 : 取各分母中相同字母或因式的最高次幂.
归纳总结
找最简公分母:
(1) 与
(2) 与
(3) 与
(4) 与
随堂小练习
例2:通分:
(1) , , (2) , ,
解:(1)中系数的最小公倍数为,字母的最高次幂为,字母的最高次幂为,故最简公分母为,
这三个分式通分后分别为: =,
= ,
.
例2:通分:(1) , , (2) , ,
解:(2)
所以这三个分式的公分母为.
这三个分式通分后分别为:=
=
=.
分式通分的一般步骤:
①确定最简公分母;
②用最简公分母分别除以各个分母求商;
③用所得的商分别乘以各分式的分子得出同分母分式.
约分和通分有什么区别和联系
归纳总结
约分 通分
联系 区别
都是根据分式的基本性质对分式进行恒等变形,不改变分式的值.
针对一个分式而言,将分式进行化简.
针对多个分式而言,将几个异分母分式化为同分母分式.
约分和通分的联系和区别:
归纳总结
1. 分式 和 的最简公分母是( C )
A. B. C. D.
C
习题1
2. 分式 与 的最简公分母是( A )
A. B.
C. D.
A
习题2
3.整式和分式 通分,可以仿照整数和分数的通分,把化成 ,此时 和 的最简公分母为 ,通分后它们的分子之和为 .
习题3
4.通分:
(1) , ; (2) , ;
解:(1)这两个分式的最简公分母为.
这两个分式通分后分别为: = ,
= .
习题4
4.通分:
(1) , ; (2) , ;
解:(2)这两个分式的公分母为.
这两个分式通分后分别为: = ,
= .
习题4
解:(3)这两个分式的公分母为
这两个分式通分后分别为: = = ,
= .
4.通分:
(3) , ; (4) , , ;
习题4
解: (4)这三个分式的公分母为
这三个分式通分后分别为: = = ,
= = ,
= = .
4.通分:(3) , ; (4) , , ;
习题4
分式的通分
分式的通分
最简公分母
异分母分式为同分母分式的过程,叫做分式的通分.
分式通分取各分母所有因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.
9.2.2 分式的加减
第一课时 分式的通分
学习目标及重难点
1.理解并掌握最简公分母的概念,能够求出几个分式的最简公分母;(重点)
2.能够对几个分式进行通分,并运用其解决问题.(难点)
算一算:
复习回顾
同分母分数相加减
算一算:
异分母分数相加减
分数的通分
依据:分数的基本性质
同分母分数相加减
关键:确定公分母
探索1:分式的通分
思考:类比分数的加减运算,下面分式的加减运算如何进行?
(1) ; (2) ;
同分母分式相加减
同分母分式相加减
思考:类比分数的加减运算,下面分式的加减运算如何进行?
(3) (4)
异分母分式相加减
分式的通分
依据:分式的基本性质
同分母分式相加减
关键:确定公分母
与分数类似,在计算异分母分式的加减时,要利用分式的基本性质,先把分母不相同的分式化成分母相同的分式,再进行加减.化异分母的分式为同分母的分式的过程,叫作分式的通分.
异分母分式通分时,关键是确定公分母.通常取各分母所有因式的最高次幂的积作为公分母,这样的公分母叫作最简公分母.
归纳总结
思考:怎么找分式的最简公分母?
观察并找出下面各组分式最简公分母:
一定系数:取各分母系数的最小公倍数;
二定因式:取各分母中出现的所有字母;
三定指数:取分母中相同字母的最高次幂.
(1)与
最简公分母:
最简公分母:
思考:怎么找分式的最简公分母?
观察并找出下面各组分式最简公分母:
一定系数:取各分母系数的最小公倍数;
二定因式:取各分母分解因式后的所有因式,不能分解因式的整体看做一个因式;
三定指数:取分母中相同因式的最高次幂.
(2) 与
因式分解
因式分解
怎样确定最简公分母呢?
(1)一定系数 : 取各分母系数的最小公倍数;
(2)二定因式 : 单项式:取各分母的所有字母.
多项式:取各分母分解因式后的所有因式,不能分解因式
的整体看做一个因式;(分母是多项式:先分解因式)
(3)三定指数 : 取各分母中相同字母或因式的最高次幂.
归纳总结
找最简公分母:
(1) 与
(2) 与
(3) 与
(4) 与
随堂小练习
例2:通分:
(1) , , (2) , ,
解:(1)中系数的最小公倍数为,字母的最高次幂为,字母的最高次幂为,故最简公分母为,
这三个分式通分后分别为: =,
= ,
.
例2:通分:(1) , , (2) , ,
解:(2)
所以这三个分式的公分母为.
这三个分式通分后分别为:=
=
=.
分式通分的一般步骤:
①确定最简公分母;
②用最简公分母分别除以各个分母求商;
③用所得的商分别乘以各分式的分子得出同分母分式.
约分和通分有什么区别和联系
归纳总结
约分 通分
联系 区别
都是根据分式的基本性质对分式进行恒等变形,不改变分式的值.
针对一个分式而言,将分式进行化简.
针对多个分式而言,将几个异分母分式化为同分母分式.
约分和通分的联系和区别:
归纳总结
1. 分式 和 的最简公分母是( C )
A. B. C. D.
C
习题1
2. 分式 与 的最简公分母是( A )
A. B.
C. D.
A
习题2
3.整式和分式 通分,可以仿照整数和分数的通分,把化成 ,此时 和 的最简公分母为 ,通分后它们的分子之和为 .
习题3
4.通分:
(1) , ; (2) , ;
解:(1)这两个分式的最简公分母为.
这两个分式通分后分别为: = ,
= .
习题4
4.通分:
(1) , ; (2) , ;
解:(2)这两个分式的公分母为.
这两个分式通分后分别为: = ,
= .
习题4
解:(3)这两个分式的公分母为
这两个分式通分后分别为: = = ,
= .
4.通分:
(3) , ; (4) , , ;
习题4
解: (4)这三个分式的公分母为
这三个分式通分后分别为: = = ,
= = ,
= = .
4.通分:(3) , ; (4) , , ;
习题4
分式的通分
分式的通分
最简公分母
异分母分式为同分母分式的过程,叫做分式的通分.
分式通分取各分母所有因式的最高次幂的积作为公分母,这样的分母叫做最简公分母.
