沪科版(2024)七年级数学下册 9.1 第1课时 分式的概念 课件(共21张PPT)
文档属性
| 名称 | 沪科版(2024)七年级数学下册 9.1 第1课时 分式的概念 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
9.1 分式及其基本性质
第一课时 分式的概念
学习目标及重难点
1.理解分式的概念,并能用分式表示现实生活中的量;
2.掌握分式有、无意义的条件及分式的值为0的条件;(重点、难点)
下列代数式中哪些是单项式?哪些是多项式?分别填入所属的圈中.
单项式
多项式
①
复习回顾
单项式和多项式统称整式.
探索1:分式的概念
问题1:一个长方形的面积为 ,如果它的长为,那么它的宽为________________
问题2:某超级杂交稻育种基地有两块稻田,第一块稻田 hm2,每公顷产超级杂交稻 kg;第二块稻田 hm2,每公顷产超级杂交稻 kg,则这两块稻田平均每公顷产超级杂交稻________________kg.
在上面问题中,列出的代数式 ,这些代数式有什么共同特征?与整式有什么不同?你还能列出几个这样的式子吗?
(1)都有分子、分母与分数线构成;
(2)分子、分母都是整式;
(3)分母中都含有字母;
不同点:它们的分母中都含有字母,而整式的分母中不含字母.
议一议
共同特征
一般地,如果 表示两个整式,并且 中含有字母,那么式子 叫作分式 . 其中叫作分式的分子,叫作分式的分母.
归纳总结
正如分数可以看成两个整数相除的商一样,分式是两个整式相除的商.
有理式
整式
分式
分式和整式统称为有理式,即
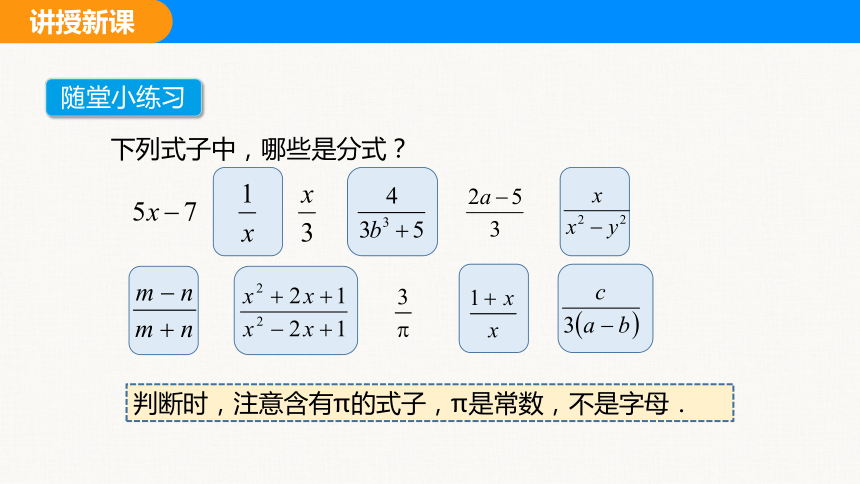
下列式子中,哪些是分式?
随堂小练习
判断时,注意含有π的式子,π是常数,不是字母.
除数不能为0
问题3:我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
探索2:分式无意义、有意义、值为零的条件
=
分母不能为0
分式 无意义的条件:分母
分式 有意义的条件:分母
问题4:在什么条件下,分式 的值为?
当时,分式 值为零.
无意义的条件
值为零的条件
当时,分式 无意义.
当时,分式 值为零.
有意义的条件
当时,分式 有意义.
归纳总结
例1:(1)当取何值时,分式 有意义
(2)当是什么数时,分式 的值为零
解(1)当分母的值等于零时,分式没有意义,除此之外,分式都有意义.
由
解得
如无特别说明,本章出现的分式都有意义,即其分母都不等于零.
例1:(1)当取何值时,分式 有意义
(2)当是什么数时,分式 的值为零
解(2) 由
解得
当时,.
因而,当时,分式 的值为零.
1.若分式 无意义,则
2.若分式 则
或
随堂小练习
A. 1个 B. 2个 C. 3个 D. 4个
B
1.下列各式: , , , 其中分式共有( )
习题1
2.若分式 的值为零,那么的值为( )
A. 或 B.
C. D.
C
习题2
3. 下列各式中,无论取何值,分式都有意义的是( )
A. B.
C. D.
D
习题3
4.下列关于分式的判断,正确的是( )
A.当时, 的值为零
B.当时, 有意义
C.无论为何值, 不可能得整数值
D.无论为何值, 的值总为正数
D
习题4
5.已知分式,当时,分式没有意义;当时,分式的值为零.求分式的值.
解:当时,分式没有意义,
说明此时,则;
当时,分式的值为零,
说明此时,则
把的值代入,得==.
习题5
概念
无意义的条件
分式的概念
值为零的条件
1.符合 的形式(为整式);
2.中含有字母,且
当时,分式 无意义.
当时,分式 值为零.
有意义的条件
当时,分式 有意义.
9.1 分式及其基本性质
第一课时 分式的概念
学习目标及重难点
1.理解分式的概念,并能用分式表示现实生活中的量;
2.掌握分式有、无意义的条件及分式的值为0的条件;(重点、难点)
下列代数式中哪些是单项式?哪些是多项式?分别填入所属的圈中.
单项式
多项式
①
复习回顾
单项式和多项式统称整式.
探索1:分式的概念
问题1:一个长方形的面积为 ,如果它的长为,那么它的宽为________________
问题2:某超级杂交稻育种基地有两块稻田,第一块稻田 hm2,每公顷产超级杂交稻 kg;第二块稻田 hm2,每公顷产超级杂交稻 kg,则这两块稻田平均每公顷产超级杂交稻________________kg.
在上面问题中,列出的代数式 ,这些代数式有什么共同特征?与整式有什么不同?你还能列出几个这样的式子吗?
(1)都有分子、分母与分数线构成;
(2)分子、分母都是整式;
(3)分母中都含有字母;
不同点:它们的分母中都含有字母,而整式的分母中不含字母.
议一议
共同特征
一般地,如果 表示两个整式,并且 中含有字母,那么式子 叫作分式 . 其中叫作分式的分子,叫作分式的分母.
归纳总结
正如分数可以看成两个整数相除的商一样,分式是两个整式相除的商.
有理式
整式
分式
分式和整式统称为有理式,即
下列式子中,哪些是分式?
随堂小练习
判断时,注意含有π的式子,π是常数,不是字母.
除数不能为0
问题3:我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
探索2:分式无意义、有意义、值为零的条件
=
分母不能为0
分式 无意义的条件:分母
分式 有意义的条件:分母
问题4:在什么条件下,分式 的值为?
当时,分式 值为零.
无意义的条件
值为零的条件
当时,分式 无意义.
当时,分式 值为零.
有意义的条件
当时,分式 有意义.
归纳总结
例1:(1)当取何值时,分式 有意义
(2)当是什么数时,分式 的值为零
解(1)当分母的值等于零时,分式没有意义,除此之外,分式都有意义.
由
解得
如无特别说明,本章出现的分式都有意义,即其分母都不等于零.
例1:(1)当取何值时,分式 有意义
(2)当是什么数时,分式 的值为零
解(2) 由
解得
当时,.
因而,当时,分式 的值为零.
1.若分式 无意义,则
2.若分式 则
或
随堂小练习
A. 1个 B. 2个 C. 3个 D. 4个
B
1.下列各式: , , , 其中分式共有( )
习题1
2.若分式 的值为零,那么的值为( )
A. 或 B.
C. D.
C
习题2
3. 下列各式中,无论取何值,分式都有意义的是( )
A. B.
C. D.
D
习题3
4.下列关于分式的判断,正确的是( )
A.当时, 的值为零
B.当时, 有意义
C.无论为何值, 不可能得整数值
D.无论为何值, 的值总为正数
D
习题4
5.已知分式,当时,分式没有意义;当时,分式的值为零.求分式的值.
解:当时,分式没有意义,
说明此时,则;
当时,分式的值为零,
说明此时,则
把的值代入,得==.
习题5
概念
无意义的条件
分式的概念
值为零的条件
1.符合 的形式(为整式);
2.中含有字母,且
当时,分式 无意义.
当时,分式 值为零.
有意义的条件
当时,分式 有意义.
