沪科版(2024)七年级数学下册 9.3 第2课时 分式方程的应用 课件 (共25张PPT)
文档属性
| 名称 | 沪科版(2024)七年级数学下册 9.3 第2课时 分式方程的应用 课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 20:00:50 | ||
图片预览






文档简介
(共25张PPT)
9.3 分式方程
第二课时 分式方程的应用
学习目标及重难点
1.进一步熟练掌握可化为一元一次方程的分式方程的解法;
2.掌握列分式方程解决实际问题.(重点、难点)
3.验根有哪几种方法?
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.通常使用第一种方法.
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
分式方程
整式方程
转化
去分母
复习回顾
探索1:公式变形在解分式方程中的应用
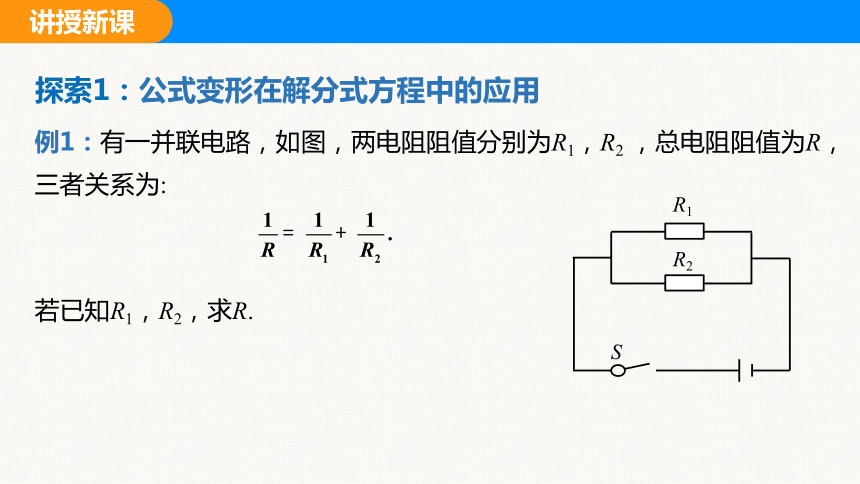
例1:有一并联电路,如图,两电阻阻值分别为R1,R2 ,总电阻阻值为R,三者关系为:
若已知R1,R2,求R.
R1
R2
S
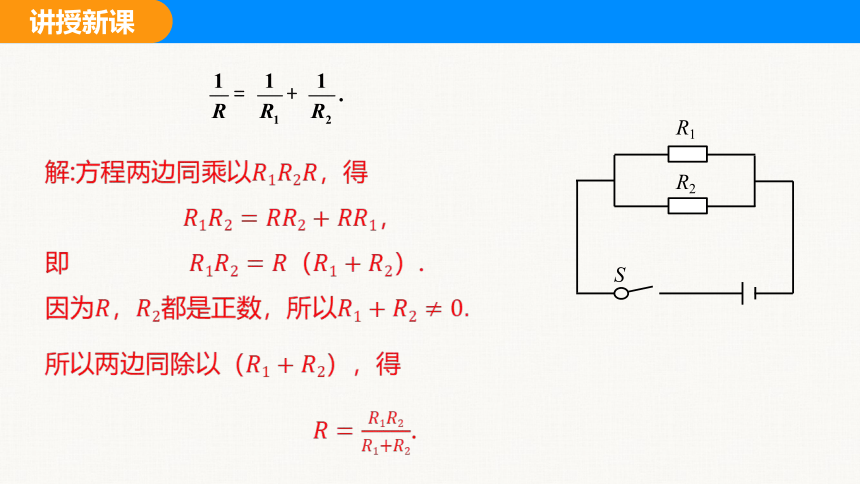
解:方程两边同乘以,得
,
即 .
因为都是正数,所以
所以两边同除以,得
.
R1
R2
S
在公式 = 中,,用表示出 .
.
解:方程两边同乘以,得
因为 ,
所以两边同除以 ,得
随堂小练习
例2:七(1)、(2)两班师生前往郊区参加义务植树活动.已知七(1)班每天比七(2)班多种10棵树.如果分配给七(1)、(2)两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
探索2:分式方程的实际应用
解:设七(2)班每天植树棵,
那么七(1)班每天植树棵,
七(1)班完成任务需 天,
七(2)班完成任务需 天.
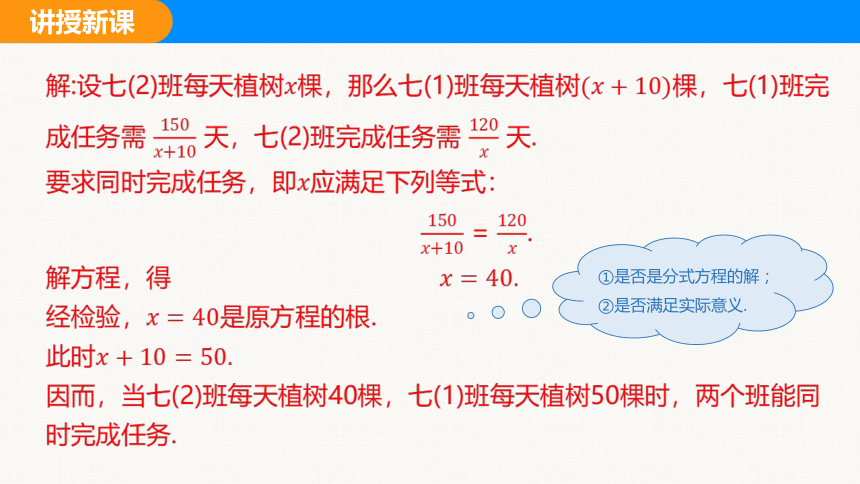
解:设七(2)班每天植树棵,那么七(1)班每天植树棵,七(1)班完成任务需 天,七(2)班完成任务需 天.
要求同时完成任务,即应满足下列等式:
= .
解方程,得
经检验,是原方程的根.
此时
因而,当七(2)班每天植树40棵,七(1)班每天植树50棵时,两个班能同时完成任务.
①是否是分式方程的解;
②是否满足实际意义.
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.(1)检验是不是所列方程的解;
(2)检验是否满足实际意义.
6.答:注意单位和语言完整.
思考:列分式方程解应用题的一般步骤是什么
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
例3:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x月.
解:设乙单独完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意得
即
方程两边都乘以2x,得
解得 x=1.
检验:当x=1时,2x≠0.
所以,原分式方程的解为 x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
x +1=2x
例3:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
等量关系:
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
设乙单独完成这项工程需要 x 月.
本题的等量关系还可以怎么找?
此时表格怎么列,方程又怎么列呢?
工作时间(月) 工作效率 工作总量(1)
甲单独
两队合作
此时方程是
1
例4:朋友们约着一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200公里时,发现小轿车只行驶了180公里,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少km/h?
0
180
200
例4:朋友们约着一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200公里时,发现小轿车只行驶了180公里,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少km/h?
路程 速度 时间
面包车
小轿车
200
180
x+10
x
设小轿车的速度为 x 千米/小时
面包车的时间=小轿车的时间
列表格如下:
等量关系:
解:设小轿车的速度为x千米/小时,则面包车速度为千米/小时,依题意得
解得x=90
经检验,x=90是原方程的解,
且x=90,x+10=100,符合题意.
答:面包车的速度为100千米/小时,小轿车的速度为90千米/小时.
例5:一轮船往返于两地之间,顺水比逆水快1小时到达.已知两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度.
(不合题意,舍去),
解:设船在静水中的速度为千米/小时,根据题意得
解得
检验得
答:船在静水中的速度为千米/小时.
方程两边同乘 得
1.已知,则可以表示为( C )
A. B. C. D.
C
习题1
2.甲、乙两船从相距300 km的A,B两地同时出发,相向而行,甲船从A地顺流航行180 km时与从B地逆流航行的乙船相遇,水流的速度为6 km/h.若甲、乙两船在静水中的速度均为 km/h,则求两船在静水中的速度可列方程为 ( )
A. = B. = C. = D. =
A
习题2
3.为提高生产效率,某工厂将生产线进行了升级改造,改造后比改造前每天多生产100件,改造后生产600件所用的时间与改造前生产400件所用的时间相同,则改造后每天生产的产品件数为( B )
A. 200 B. 300 C. 400 D. 500
B
习题3
4.某旅行社组织游客从地出发到地的航天科技馆参观,已知地到地的路程为 km,乘坐型车比乘坐型车少用 h,型车的平均速度是型车的平均速度的倍,求型车的平均速度.
解:设型车的平均速度是 km/h,则型车的平均速度是 km/h.
根据题意,得 ,
解得.
经检验,是所列方程的解,且符合题意.
答:型车的平均速度是 km/h.
习题4
5.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克. 以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
解析:根据第二次购买水果数多20千克,可得出方程,解出即可得出答案;
习题5
解:(1)设第一次购买的单价为x元,则第二次的单价为1.1x元,
根据题意得
解得 x=6.
经检验,x=6是原方程的解.
答:第一次水果的进价为每千克6元.
,
5.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克.
(1)求第一次水果的进价是每千克多少元?
解析:(2)先计算两次购买水果的数量,赚钱情况:销售的水果量×(实际售价-当次进价),两次合计,就可以求得是盈利还是亏损了.
5.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克. 以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
(2)第一次购买水果1200÷6=200(千克).
第二次购买水果200+20=220(千克).
第一次赚钱为200×(86)=400(元),
第二次赚钱为100×(96.6)+120×(9×0.56.6)=12(元).
所以两次共赚钱40012=388(元).
5.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克. 以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
分式方程的应用
步骤
类型
行程问题、工程问题、数字问题、顺逆问题、利润问题等
一审二设三列四解五验六答
9.3 分式方程
第二课时 分式方程的应用
学习目标及重难点
1.进一步熟练掌握可化为一元一次方程的分式方程的解法;
2.掌握列分式方程解决实际问题.(重点、难点)
3.验根有哪几种方法?
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.通常使用第一种方法.
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
分式方程
整式方程
转化
去分母
复习回顾
探索1:公式变形在解分式方程中的应用
例1:有一并联电路,如图,两电阻阻值分别为R1,R2 ,总电阻阻值为R,三者关系为:
若已知R1,R2,求R.
R1
R2
S
解:方程两边同乘以,得
,
即 .
因为都是正数,所以
所以两边同除以,得
.
R1
R2
S
在公式 = 中,,用表示出 .
.
解:方程两边同乘以,得
因为 ,
所以两边同除以 ,得
随堂小练习
例2:七(1)、(2)两班师生前往郊区参加义务植树活动.已知七(1)班每天比七(2)班多种10棵树.如果分配给七(1)、(2)两班的植树任务分别是150棵和120棵,问两个班每天各植树多少棵,才能同时完成任务?
探索2:分式方程的实际应用
解:设七(2)班每天植树棵,
那么七(1)班每天植树棵,
七(1)班完成任务需 天,
七(2)班完成任务需 天.
解:设七(2)班每天植树棵,那么七(1)班每天植树棵,七(1)班完成任务需 天,七(2)班完成任务需 天.
要求同时完成任务,即应满足下列等式:
= .
解方程,得
经检验,是原方程的根.
此时
因而,当七(2)班每天植树40棵,七(1)班每天植树50棵时,两个班能同时完成任务.
①是否是分式方程的解;
②是否满足实际意义.
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.(1)检验是不是所列方程的解;
(2)检验是否满足实际意义.
6.答:注意单位和语言完整.
思考:列分式方程解应用题的一般步骤是什么
工作时间(月) 工作效率 工作总量(1)
甲队
乙队
例3:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x月.
解:设乙单独完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意得
即
方程两边都乘以2x,得
解得 x=1.
检验:当x=1时,2x≠0.
所以,原分式方程的解为 x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
x +1=2x
例3:两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
等量关系:
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
设乙单独完成这项工程需要 x 月.
本题的等量关系还可以怎么找?
此时表格怎么列,方程又怎么列呢?
工作时间(月) 工作效率 工作总量(1)
甲单独
两队合作
此时方程是
1
例4:朋友们约着一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200公里时,发现小轿车只行驶了180公里,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少km/h?
0
180
200
例4:朋友们约着一起开着2辆车自驾去黄山玩,其中面包车为领队,小轿车紧随其后,他们同时出发,当面包车行驶了200公里时,发现小轿车只行驶了180公里,若面包车的行驶速度比小轿车快10km/h,请问面包车,小轿车的速度分别为多少km/h?
路程 速度 时间
面包车
小轿车
200
180
x+10
x
设小轿车的速度为 x 千米/小时
面包车的时间=小轿车的时间
列表格如下:
等量关系:
解:设小轿车的速度为x千米/小时,则面包车速度为千米/小时,依题意得
解得x=90
经检验,x=90是原方程的解,
且x=90,x+10=100,符合题意.
答:面包车的速度为100千米/小时,小轿车的速度为90千米/小时.
例5:一轮船往返于两地之间,顺水比逆水快1小时到达.已知两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度.
(不合题意,舍去),
解:设船在静水中的速度为千米/小时,根据题意得
解得
检验得
答:船在静水中的速度为千米/小时.
方程两边同乘 得
1.已知,则可以表示为( C )
A. B. C. D.
C
习题1
2.甲、乙两船从相距300 km的A,B两地同时出发,相向而行,甲船从A地顺流航行180 km时与从B地逆流航行的乙船相遇,水流的速度为6 km/h.若甲、乙两船在静水中的速度均为 km/h,则求两船在静水中的速度可列方程为 ( )
A. = B. = C. = D. =
A
习题2
3.为提高生产效率,某工厂将生产线进行了升级改造,改造后比改造前每天多生产100件,改造后生产600件所用的时间与改造前生产400件所用的时间相同,则改造后每天生产的产品件数为( B )
A. 200 B. 300 C. 400 D. 500
B
习题3
4.某旅行社组织游客从地出发到地的航天科技馆参观,已知地到地的路程为 km,乘坐型车比乘坐型车少用 h,型车的平均速度是型车的平均速度的倍,求型车的平均速度.
解:设型车的平均速度是 km/h,则型车的平均速度是 km/h.
根据题意,得 ,
解得.
经检验,是所列方程的解,且符合题意.
答:型车的平均速度是 km/h.
习题4
5.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克. 以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
解析:根据第二次购买水果数多20千克,可得出方程,解出即可得出答案;
习题5
解:(1)设第一次购买的单价为x元,则第二次的单价为1.1x元,
根据题意得
解得 x=6.
经检验,x=6是原方程的解.
答:第一次水果的进价为每千克6元.
,
5.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克.
(1)求第一次水果的进价是每千克多少元?
解析:(2)先计算两次购买水果的数量,赚钱情况:销售的水果量×(实际售价-当次进价),两次合计,就可以求得是盈利还是亏损了.
5.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克. 以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
(2)第一次购买水果1200÷6=200(千克).
第二次购买水果200+20=220(千克).
第一次赚钱为200×(86)=400(元),
第二次赚钱为100×(96.6)+120×(9×0.56.6)=12(元).
所以两次共赚钱40012=388(元).
5.佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克. 以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
分式方程的应用
步骤
类型
行程问题、工程问题、数字问题、顺逆问题、利润问题等
一审二设三列四解五验六答
