第二章 一元一次不等式和一元一次不等式组 单元检测试卷(含解析)
文档属性
| 名称 | 第二章 一元一次不等式和一元一次不等式组 单元检测试卷(含解析) |

|
|
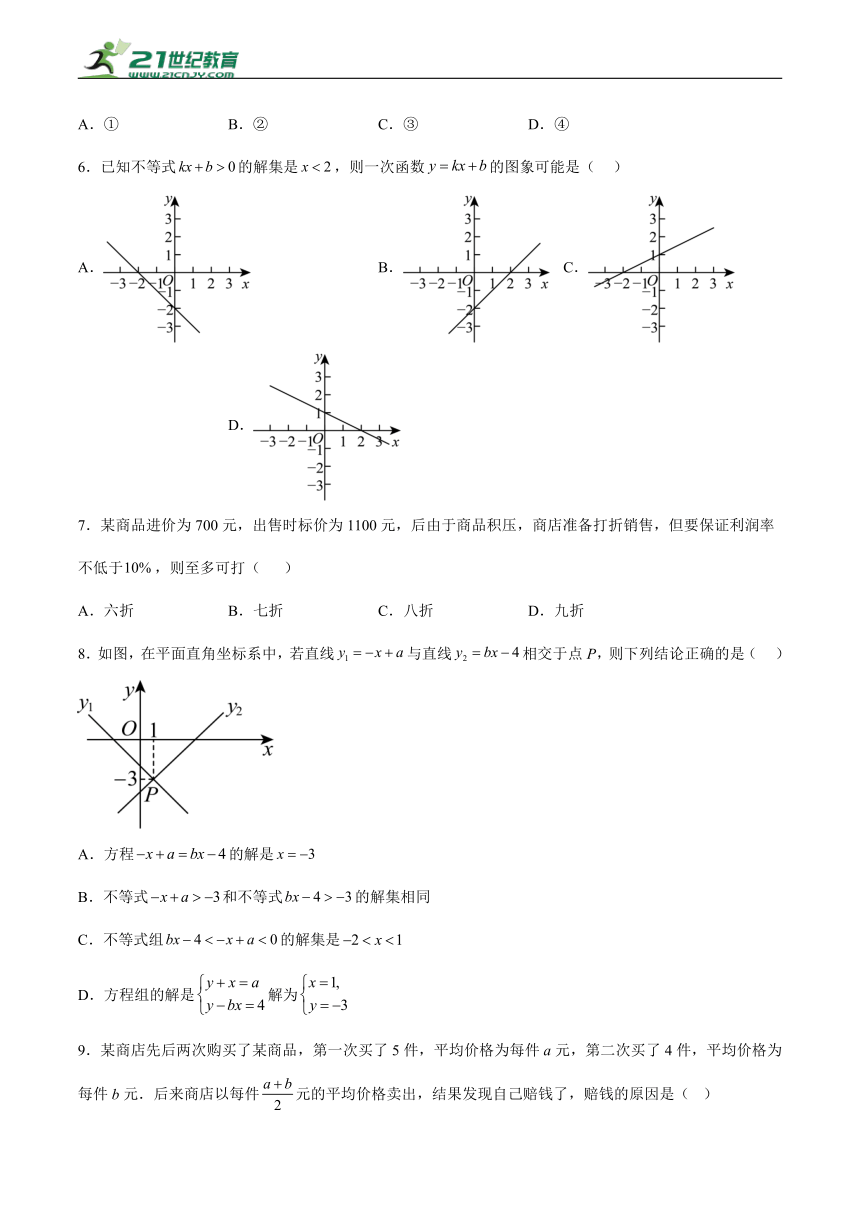
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 00:00:00 | ||
图片预览



文档简介
2025北师大版八年级数学下册第二章单元检测试卷
一、选择题(本大题共10小题,每小题2分,共20分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.数学表达式①;②;③;④;⑤中不等式的个数是( )
A.个 B.个 C.个 D.个
2.下列说法错误的是( )
A.是不等式的解 B.是不等式的解
C.的解集是 D.的解集就是、、
3.设、为实数,则下列说法正确的是( )
A.,则 B.若,,则
C.若,,则 D.若,则
4.不等式组的解集在数轴上的表示正确的是( )
A. B.
C. D.
5.下面是晓晓的一次数学课后作业,请帮助晓晓检查一下她的解题过程.
解不等式. 解:去分母,得. …………① 去括号,得. …………② 移项,得. …………③ 合并同类项,得. …………④ 系数化为1,得. …………⑤
晓晓的解题过程开始错误的一步是( )
A.① B.② C.③ D.④
6.已知不等式的解集是,则一次函数的图象可能是( )
A. B. C. D.
7.某商品进价为700元,出售时标价为1100元,后由于商品积压,商店准备打折销售,但要保证利润率不低于,则至多可打( )
A.六折 B.七折 C.八折 D.九折
8.如图,在平面直角坐标系中,若直线与直线相交于点P,则下列结论正确的是( )
A.方程的解是
B.不等式和不等式的解集相同
C.不等式组的解集是
D.方程组的解是解为
9.某商店先后两次购买了某商品,第一次买了5件,平均价格为每件a元,第二次买了4件,平均价格为每件b元.后来商店以每件元的平均价格卖出,结果发现自己赔钱了,赔钱的原因是( )
A. B. C. D.
10.关于x的不等式组有四个整数解,则a的取值范围是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.根据“a的3倍与2的差小于0”列出的不等式是: .
12.如果不等式的解集是,那么a必须满足 .
13.某商场计划购进甲、乙两种商品共100件.甲种商品每件进价15元,乙种商品每件进价35元,且购进两种商品的总费用不超过2700元,则购进甲种商品不少于 件.
14.若关于x 的方程的解是负数,则m的取值范围是 .
15.设表示x,y两个数中的最大值.例如“”.则关于x的函数的最小值为 .
16.如图,钢架中,,焊上等长的钢条,,,…来加固钢架.若,且恰好用了根钢条,则的取值范围是 .
三、解答题(本大题共7小题,共62分.解答时应写出文字说明、证明过程或演算步骤)
17.解不等式(组):
(1);
(2),并把它的解集表示在数轴上.
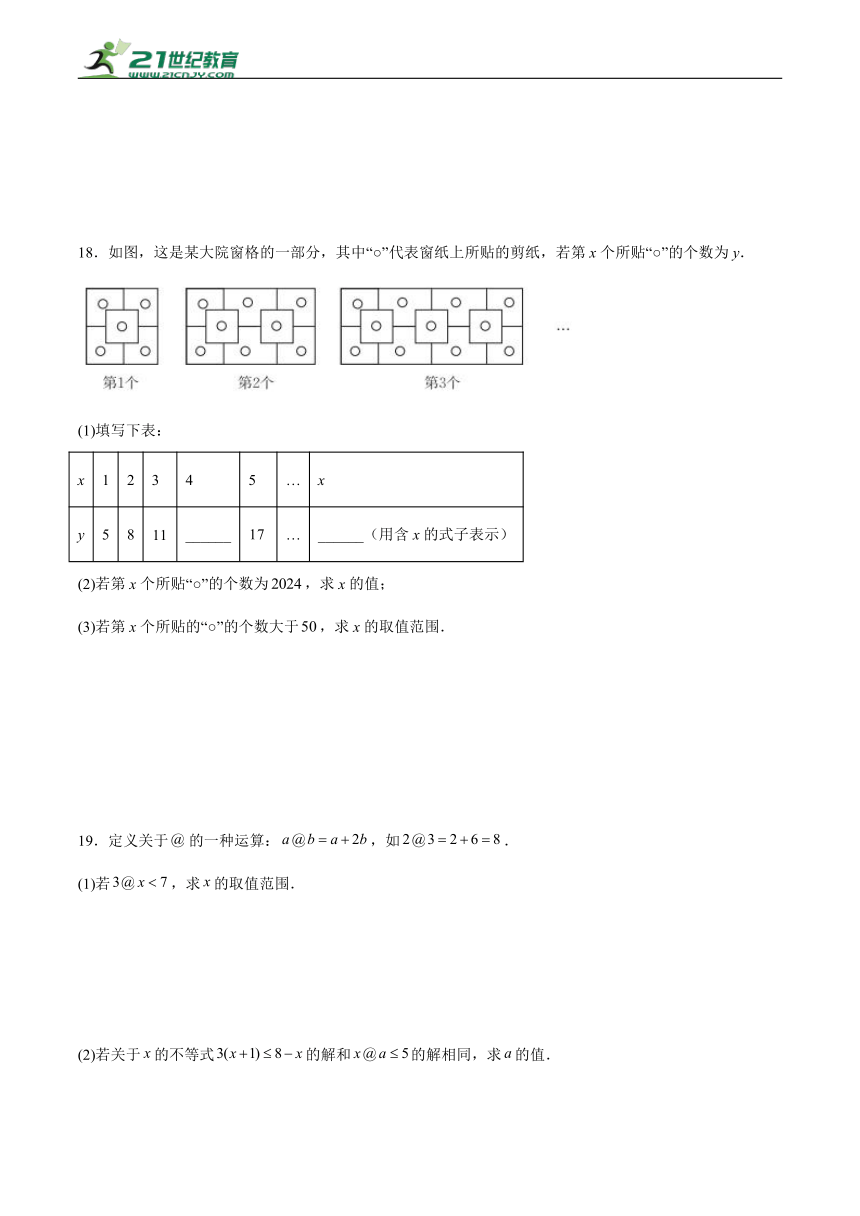
18.如图,这是某大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,若第x个所贴“○”的个数为y.
(1)填写下表:
x 1 2 3 4 5 … x
y 5 8 ______ … ______(用含x的式子表示)
(2)若第x个所贴“○”的个数为,求x的值;
(3)若第x个所贴的“○”的个数大于,求x的取值范围.
19.定义关于的一种运算:,如.
(1)若,求的取值范围.
(2)若关于的不等式的解和的解相同,求的值.
20.已知方程组的解满足x为非正数,y为负数.
(1)求m得取值范围.
(2)在m的取值范围内,当m为何整数时,不等式的解为.
21.如图,在平面直角坐标系中,一次函数(、为常数且)的图象经过点,且与正比例函数的图象交于点.
(1)求的值及一次函数的表达式;
(2)关于的不等式的解集为 ;
(3)直线上存在点,满足的面积是的面积倍,则点的坐标为 .
22.如图,在中,,射线,点从点出发沿射线以的速度运动,当点出发后,点也从点出发沿射线以的速度运动,分别连接,,.设点运动时间为,其中.
(1)若,则的取值范围是______;
(2)求为何值时,平分的面积;
(3)求为何值时,.
23.一家电脑公司有A型、B型、C型三种型号的电脑,其中A型每台6000元、B型每台4000元、C型每台2500元.某中学计划从这家电脑公司购进电脑.
(1)若该中学只购买A型电脑和B型电脑,且购买A型电脑的数量比购买B型电脑的数量的一半还少1台,要求购买的总价不超过90000元,则最多可以购买多少台A型电脑?
(2)若该中学现有专项资金100500元,计划从这家电脑公司购进36台两种型号的电脑,且这笔资金恰好全用完.请你设计几种不同的购买方案供这个学校选择,并说明理由.
(3)这家电脑公司为提高B型电脑销量,设计了旧电脑抵值活动:购买一台B型电脑时,可以用一台旧电脑抵值1000元.该中学计划只购买B型电脑,拿出的旧电脑和购买的B型电脑数量一共是30台.若要使购买B型电脑的数量是旧电脑数量的2倍,且购买B型电脑的实际总费用不少于100000元,则要在计划的基础上再多买a台B型电脑,此时该中学需要再拿出台的旧电脑参加抵值活动,求该中学至少需要再拿出多少台旧电脑进行抵值?
参考答案
一、选择题(本大题共10小题,每小题2分,共20分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.数学表达式①;②;③;④;⑤中不等式的个数是( )
A.个 B.个 C.个 D.个
【答案】C
【分析】根据不等式的定义(用符号“”或“”表示大小关系的式子,叫做不等式)逐个判断即可得.
【详解】解:①,②;⑤都是不等式,共有3个,
故选:C.
【点睛】本题考查了不等式的定义,熟记不等式的定义是解题关键.
2.下列说法错误的是( )
A.是不等式的解 B.是不等式的解
C.的解集是 D.的解集就是、、
【答案】D
【分析】根据不等式的性质即可求解.
【详解】解:A选项,是不等式的解,把代入不等式,不等式成立,故正确;
B选项,是不等式的解,把代入不等式,不等式成立,故正确;
C选项,的解集是,解不等式得,故正确;
D选项,的解集就是、、,不是不等式的解,故错误.
故选:D.
【点睛】本题主要考查不等式的性质解一元一次不等式,掌握不等式的性质是解题的关键.
3.设、为实数,则下列说法正确的是( )
A.,则 B.若,,则
C.若,,则 D.若,则
【答案】B
【分析】本题考查了不等式的性质“性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变;性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变;性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变”,熟练掌握不等式的性质是解题关键.根据不等式的性质逐项判断即可得.
【详解】解:A、若,则,不能确定,所以此项说法错误,不符合题意;
B、若,,则,所以,此项说法正确,符合题意;
C、若,,则,所以此项说法错误,不符合题意;
D、若,则或,所以不一定大于0,此项说法错误,不符合题意;
故选:B.
4.不等式组的解集在数轴上的表示正确的是( )
A. B.
C. D.
【答案】D
【分析】本题考查了解一元一次不等式组、在数轴上表示不等式组的解集,熟练掌握不等式组的解法是解题关键.先分别求出两个不等式的解集,再在数轴上表示不等式组的解集即可得.
【详解】解:,
解不等式①得:,
解不等式②得:,
在数轴上表示不等式组的解集如下:
故选:D.
5.下面是晓晓的一次数学课后作业,请帮助晓晓检查一下她的解题过程.
解不等式. 解:去分母,得. …………① 去括号,得. …………② 移项,得. …………③ 合并同类项,得. …………④ 系数化为1,得. …………⑤
晓晓的解题过程开始错误的一步是( )
A.① B.② C.③ D.④
【答案】A
【分析】此题考查了解一元一次不等式,根据解一元一次不等式的步骤求解即可得到答案.
【详解】解:.
去分母,得. …………①
去括号,得. …………②
移项,得. …………③
合并同类项,得. …………④
系数化为1,得. …………⑤
由解题过程可知,晓晓的解题过程开始错误的一步是①,
故选:A
6.已知不等式的解集是,则一次函数的图象可能是( )
A. B. C. D.
【答案】D
【分析】本题考查了一次函数的图象,解不等式,由不等式可得,进而由不等式的解集可得,,即得到一次函数的图象经过一、二、四象限,据此即可求解,由不等式的解集确定出的符号是解题的关键.
【详解】解:∵不等式,
∴,
∵不等式的解集是,
∴,,
∴一次函数的图象经过一、二、四象限,
故选:.
7.某商品进价为700元,出售时标价为1100元,后由于商品积压,商店准备打折销售,但要保证利润率不低于,则至多可打( )
A.六折 B.七折 C.八折 D.九折
【答案】B
【分析】设最多可打x折,根据题意,得,求整数解即可.
本题考查了一元一次不等式的应用,打折问题,正确理解,列出不等式解答是关键.
【详解】解:设最多可打x折,
根据题意,得,
解得.
故最多打7折,
故选B.
8.如图,在平面直角坐标系中,若直线与直线相交于点P,则下列结论正确的是( )
A.方程的解是
B.不等式和不等式的解集相同
C.不等式组的解集是
D.方程组的解是解为
【答案】C
【分析】本题考查一次函数的图象和性质.由图象可得直线与直线相交于点即可判断选项A;由图象可得的解集为,由图象可得的解集为,即可判断选项B;求出的解集是,当时,,即可判断选项C;由图象可得方程组的解为,即可判断选项D.
【详解】解:A.由图象可得直线与直线相交于点,
∴方程的解是,
故选项错误,不符合题意;
B.由图象可得的解集为,
由图象可得的解集为,
∴不等式和不等式的解集不相同,
故选项错误,不符合题意;
C.将代入得,
解得,
∴,
将代入得,
由图象可知,的解集是,
由图象可知,当时,直线在直线的下方,
∴当时,,
∴不等式组的解集是,
故选项正确,符合题意;
D.∵直线与直线相交于点P,
∴方程组的解为,
故选项错误,不符合题意.
故选:C.
9.某商店先后两次购买了某商品,第一次买了5件,平均价格为每件a元,第二次买了4件,平均价格为每件b元.后来商店以每件元的平均价格卖出,结果发现自己赔钱了,赔钱的原因是( )
A. B. C. D.
【答案】A
【分析】本题主要考查不等式的性质,解决问题的关键是读懂题意,找到关键描述语,联系实际,进而找到所求的量之间的不等关系.
首先表示9件商品的平均价格为 元,而以每件元的价格把商品全部卖掉,结果赔了钱,所以有,继而得出a和b的关系.
【详解】解:∵9件商品的平均价格为 元,
∵商店以每件元的平均价格卖出,结果发现自己赔钱了,
∴ ,
解得:,
故选:A.
10.关于x的不等式组有四个整数解,则a的取值范围是( )
A. B. C. D.
【答案】A
【分析】本题考查不等式组的解集,首先解出不等式的解集,再根据不等式组有且只有四个整数解,得到a的取值范围.
【详解】解:解不等式得,,
解不等式得,,
∵关于x的不等式组有四个整数解,而的四个整数是9,10,11,12,
∴,
解得,
∴a的取值范围是,
故选:A.
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.根据“a的3倍与2的差小于0”列出的不等式是: .
【答案】3a﹣2<0
【分析】关键描述语是:差小于0,应先算a的3倍,再算差.
【详解】根据题意,得3a﹣2<0.
故答案为:3a﹣2<0.
【点睛】本题考查了由实际问题抽象出一元一次不等式,读懂题意,抓住关键词语,弄清运算的先后顺序和不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.
12.如果不等式的解集是,那么a必须满足 .
【答案】
【分析】根据两边同时除以a-2,不等号的方向改变,可得a-2<0.
【详解】解:∵不等式(a-2)x>a-2的解集是x<1,
∴a-2<0,
解得,a<2.
故答案为:a<2.
【点睛】本题考查了不等式的性质.注意:不等式两边同除以同一个负数时,不等号的方向改变.同理,当不等式两边同时除以一个数后不等号的方向改变,也可以知道不等式两边同时除以的是一个负数.
13.某商场计划购进甲、乙两种商品共100件.甲种商品每件进价15元,乙种商品每件进价35元,且购进两种商品的总费用不超过2700元,则购进甲种商品不少于 件.
【答案】40
【分析】本题考查不等式的实际应用,设购进甲种商品为件,根据购进两种商品的总费用不超过2700元,列出不等式进行求解即可.
【详解】解:设购进甲种商品为件,则购进乙种商品件,由题意,得:
,
解得:;
答:购进甲种商品不少于40件;
故答案为:40.
14.若关于x 的方程的解是负数,则m的取值范围是 .
【答案】
【分析】本题考查解一元一次方程、一元一次不等式,先解方程得,即可得,再求解即可.
【详解】解:,
去分母得,,
去括号得,,
∴,
∵原方程的解是负数,
∴,
解得,
故答案为:.
15.设表示x,y两个数中的最大值.例如“”.则关于x的函数的最小值为 .
【答案】/
【分析】本题主要考查一次函数的性质,根据题意正确画出图形并灵活运用数形结合是解答本题的关键.根据题意画出画在同一个坐标系中,再利用数形结合确定图形即可确定最小值.
【详解】解:如图:将画在同一个坐标系中,
令,
解得:,
则两条直线交点为,
当时,函数,最小值为;
当时,函数,最小值为;
综上,关于x的函数的最小值为,
故答案为:.
16.如图,钢架中,,焊上等长的钢条,,,…来加固钢架.若,且恰好用了根钢条,则的取值范围是 .
【答案】
【分析】此题考查了等腰三角形的性质,一元一次不等式组,以及三角形的外角性质,掌握以上知识点是解答本题的关键.
根据等腰三角形的性质可得到几组相等的角,再根据三角形外角的性质可得到与之间的关系,从而不难求解.
【详解】解:,,,,
,,,,
,
要使得这样的钢条恰好焊上根,
,
由题意得:,
,
故答案为:.
三、解答题(本大题共7小题,共62分.解答时应写出文字说明、证明过程或演算步骤)
17.解不等式(组):
(1);
(2),并把它的解集表示在数轴上.
【答案】(1)
(2),见解析
【分析】本题考查解一元一次不等式和解一元一次不等式组,正确求出每一个不等式的解集是基础,熟知几个不等式的解集的公共部分的找法是解题关键.
(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得解集;
(2)分别求出每一个不等式的解集,根据求不等式组解集的规律求出不等式组的解集,最后在数轴上表示出不等式组的解集即可.
【详解】(1)解:去括号,得,
移项得:,
合并同类项,得,
系数化为1,得.
(2)解不等式,得,
解不等式,得,
则不等式组的解集为.
将不等式组的解集表示在数轴上如下:
18.如图,这是某大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,若第x个所贴“○”的个数为y.
(1)填写下表:
x 1 2 3 4 5 … x
y 5 8 ______ … ______(用含x的式子表示)
(2)若第x个所贴“○”的个数为,求x的值;
(3)若第x个所贴的“○”的个数大于,求x的取值范围.
【答案】(1),
(2)
(3)
【分析】(1)根据图形规律可得,;,,,,进而得出答案;
(2)根据(1)中得出的规律列出方程,求解即可;
(3)根据(1)中的结论列出不等式,求解即可.
【详解】(1)解:根据题意:,;
,;
,;
,;
∴;
故答案为:,;
(2)根据题意可得:,
解得:;
(3)根据题意可得:,
解得:.
【点睛】本题考查了图形的变化规律,一元一次方程的应用,一元一次不等式的应用,读懂题意,得出图形的变化规律是解本题的关键.
19.定义关于的一种运算:,如.
(1)若,求的取值范围.
(2)若关于的不等式的解和的解相同,求的值.
【答案】(1)
(2)
【分析】()根据新定义运算列出不等式即可求解;
()分别求出两个不等式的解集,再根据解集相同即可求解;
本题考查了新定义,解一元一次不等式,理解新定义是解题的关键.
【详解】(1)解:由题意得,,
∴,
∴;
(2)解:解不等式得,,
由得,,
∴,
∵不等式的解和的解相同,
∴,
解得.
20.已知方程组的解满足x为非正数,y为负数.
(1)求m得取值范围.
(2)在m的取值范围内,当m为何整数时,不等式的解为.
【答案】(1)
(2)
【分析】本题主要考查了解二元一次方程组,求一元一次不等式组的整数解,根据不等式的解集求参数:
(1)先利用加减消元法求出方程组的解为,进而得到,解不等式组即可得到答案;
(2)先把原不等式变形为,根据解集为得到,进而求出,据此可得答案.
【详解】(1)解:
得:,解得,
把代入①得:,解得,
∴方程组的解为,
∵x为非正数,y为负数,
∴,,
∴,
解得,
∴m的取值范围是.
(2)解:将不等式整理,得,
∵其解集为,
∴,
解得
∴.
结合m取整数,可得,
即当时,不等式的解集为.
21.如图,在平面直角坐标系中,一次函数(、为常数且)的图象经过点,且与正比例函数的图象交于点.
(1)求的值及一次函数的表达式;
(2)关于的不等式的解集为 ;
(3)直线上存在点,满足的面积是的面积倍,则点的坐标为 .
【答案】(1),;
(2);
(3)或.
【分析】本题考出来一次函数与一元一次不等式的关系,掌握待定系数法、三角形面积公式及数形结合思想是解题的关键.
(1)根据待定系数法求解;
(2)根据数形结合思想求解;
(3)根据三角形的面积公式求解.
【详解】(1)解:由题意得:,
解得,
,
解得:
一次函数的表达式为:;
(2)解:由图象得,当时,,
故答案为;
(3)解:设,
由题意得:,
解得:或,
或,
或,
故答案为:或.
22.如图,在中,,射线,点从点出发沿射线以的速度运动,当点出发后,点也从点出发沿射线以的速度运动,分别连接,,.设点运动时间为,其中.
(1)若,则的取值范围是______;
(2)求为何值时,平分的面积;
(3)求为何值时,.
【答案】(1)
(2)2.5秒
(3)秒或12秒
【分析】(1)根据当时,点F在线段上运动可得答案;
(2)根据当平分的面积时,点F是线段的中点可得答案;
(3)分类讨论:当点F在点C左侧时,点F再点C的右侧时,可得关于t的一元一次方程,根据解方程,可得答案;
【详解】(1)当时,,
∴,
解得,
故答案为:;
(2)∵平分的面积,
∴,
∴,
∴;
(3)分两种情况讨论:
①点F在点C左侧时,,
则,
解得;
②当点F在点C的右侧时,,
则,
解得,
综上所述,或12时,;
【点睛】本题考查了一元一次不等式的应用,一元一次方程的应用,三角形中线的性质,数形结合是解答本题的关键.
23.一家电脑公司有A型、B型、C型三种型号的电脑,其中A型每台6000元、B型每台4000元、C型每台2500元.某中学计划从这家电脑公司购进电脑.
(1)若该中学只购买A型电脑和B型电脑,且购买A型电脑的数量比购买B型电脑的数量的一半还少1台,要求购买的总价不超过90000元,则最多可以购买多少台A型电脑?
(2)若该中学现有专项资金100500元,计划从这家电脑公司购进36台两种型号的电脑,且这笔资金恰好全用完.请你设计几种不同的购买方案供这个学校选择,并说明理由.
(3)这家电脑公司为提高B型电脑销量,设计了旧电脑抵值活动:购买一台B型电脑时,可以用一台旧电脑抵值1000元.该中学计划只购买B型电脑,拿出的旧电脑和购买的B型电脑数量一共是30台.若要使购买B型电脑的数量是旧电脑数量的2倍,且购买B型电脑的实际总费用不少于100000元,则要在计划的基础上再多买a台B型电脑,此时该中学需要再拿出台的旧电脑参加抵值活动,求该中学至少需要再拿出多少台旧电脑进行抵值?
【答案】(1)最多可以购买5台A型电脑
(2)有两种方案供这个学校选择:第一种方案是购进A型电脑3台、C型电脑33台;第二种方案是购进B型电脑7台、C型电脑29台
(3)该中学至少需要再拿出4台旧电脑进行抵值
【分析】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程组;(3)根据各数量之间的关系,正确列出一元一次不等式.
(1)设购买台型电脑,则购买台型电脑,利用总价单价数量,结合总价不超过90000元,可列出关于的一元一次不等式,解之可得出的取值范围,再结合,均为正整数,即可找出的最大值;
(2)利用平均价格总价单价,可求出平均价格,结合,,三种型号电脑的单价,可得出可能有两种情况,①购买型电脑和型电脑,设购买台型电脑,台型电脑,利用总价单价数量,结合用100500元购买36台两种型号的电脑,可列出关于,的二元一次方程组,解之可得出结论;②购买型电脑和型电脑,设购买台型电脑,台型电脑,利用总价单价数量,结合用100500元购买36台两种型号的电脑,可列出关于,的二元一次方程组,解之可得出结论;
(3)设原计划购买台型电脑,则原计划拿出台旧电脑,根据购买型电脑的数量是旧电脑数量的2倍,可列出关于,的二元一次方程,变形后可得出,利用总价单价数量,结合购买型电脑的实际总费用不少于100000元,可列出关于的一元一次不等式,解之可得出的取值范围,再结合,均为正整数,即可找出的最小值为6.
【详解】(1)解:设购买台型电脑,则购买台型电脑,
根据题意得:,
解得:,
,均为正整数,
的最大值为12,的最大值为5.
答:最多可以购买5台型电脑;
(2)解:共有2种购买方案,
方案1:购买3台型电脑,33台型电脑;
方案2:购买7台型电脑,29台型电脑,理由如下:
(元,,
可能有两种情况.
①购买型电脑和型电脑,设购买台型电脑,台型电脑,
根据题意得:,
解得:,
购买3台型电脑,33台型电脑;
②购买型电脑和型电脑,设购买台型电脑,台型电脑,
根据题意得:,
解得:,
购买7台型电脑,29台型电脑.
共有2种购买方案,
方案1:购买3台型电脑,33台型电脑;
方案2:购买7台型电脑,29台型电脑;
(3)解:设原计划购买台型电脑,则原计划拿出台旧电脑,
根据题意得:,
.
购买型电脑的实际总费用不少于100000元,
,
即,
解得:,
.
答:该中学至少需要再拿出4台旧电脑进行抵值.
一、选择题(本大题共10小题,每小题2分,共20分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.数学表达式①;②;③;④;⑤中不等式的个数是( )
A.个 B.个 C.个 D.个
2.下列说法错误的是( )
A.是不等式的解 B.是不等式的解
C.的解集是 D.的解集就是、、
3.设、为实数,则下列说法正确的是( )
A.,则 B.若,,则
C.若,,则 D.若,则
4.不等式组的解集在数轴上的表示正确的是( )
A. B.
C. D.
5.下面是晓晓的一次数学课后作业,请帮助晓晓检查一下她的解题过程.
解不等式. 解:去分母,得. …………① 去括号,得. …………② 移项,得. …………③ 合并同类项,得. …………④ 系数化为1,得. …………⑤
晓晓的解题过程开始错误的一步是( )
A.① B.② C.③ D.④
6.已知不等式的解集是,则一次函数的图象可能是( )
A. B. C. D.
7.某商品进价为700元,出售时标价为1100元,后由于商品积压,商店准备打折销售,但要保证利润率不低于,则至多可打( )
A.六折 B.七折 C.八折 D.九折
8.如图,在平面直角坐标系中,若直线与直线相交于点P,则下列结论正确的是( )
A.方程的解是
B.不等式和不等式的解集相同
C.不等式组的解集是
D.方程组的解是解为
9.某商店先后两次购买了某商品,第一次买了5件,平均价格为每件a元,第二次买了4件,平均价格为每件b元.后来商店以每件元的平均价格卖出,结果发现自己赔钱了,赔钱的原因是( )
A. B. C. D.
10.关于x的不等式组有四个整数解,则a的取值范围是( )
A. B. C. D.
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.根据“a的3倍与2的差小于0”列出的不等式是: .
12.如果不等式的解集是,那么a必须满足 .
13.某商场计划购进甲、乙两种商品共100件.甲种商品每件进价15元,乙种商品每件进价35元,且购进两种商品的总费用不超过2700元,则购进甲种商品不少于 件.
14.若关于x 的方程的解是负数,则m的取值范围是 .
15.设表示x,y两个数中的最大值.例如“”.则关于x的函数的最小值为 .
16.如图,钢架中,,焊上等长的钢条,,,…来加固钢架.若,且恰好用了根钢条,则的取值范围是 .
三、解答题(本大题共7小题,共62分.解答时应写出文字说明、证明过程或演算步骤)
17.解不等式(组):
(1);
(2),并把它的解集表示在数轴上.
18.如图,这是某大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,若第x个所贴“○”的个数为y.
(1)填写下表:
x 1 2 3 4 5 … x
y 5 8 ______ … ______(用含x的式子表示)
(2)若第x个所贴“○”的个数为,求x的值;
(3)若第x个所贴的“○”的个数大于,求x的取值范围.
19.定义关于的一种运算:,如.
(1)若,求的取值范围.
(2)若关于的不等式的解和的解相同,求的值.
20.已知方程组的解满足x为非正数,y为负数.
(1)求m得取值范围.
(2)在m的取值范围内,当m为何整数时,不等式的解为.
21.如图,在平面直角坐标系中,一次函数(、为常数且)的图象经过点,且与正比例函数的图象交于点.
(1)求的值及一次函数的表达式;
(2)关于的不等式的解集为 ;
(3)直线上存在点,满足的面积是的面积倍,则点的坐标为 .
22.如图,在中,,射线,点从点出发沿射线以的速度运动,当点出发后,点也从点出发沿射线以的速度运动,分别连接,,.设点运动时间为,其中.
(1)若,则的取值范围是______;
(2)求为何值时,平分的面积;
(3)求为何值时,.
23.一家电脑公司有A型、B型、C型三种型号的电脑,其中A型每台6000元、B型每台4000元、C型每台2500元.某中学计划从这家电脑公司购进电脑.
(1)若该中学只购买A型电脑和B型电脑,且购买A型电脑的数量比购买B型电脑的数量的一半还少1台,要求购买的总价不超过90000元,则最多可以购买多少台A型电脑?
(2)若该中学现有专项资金100500元,计划从这家电脑公司购进36台两种型号的电脑,且这笔资金恰好全用完.请你设计几种不同的购买方案供这个学校选择,并说明理由.
(3)这家电脑公司为提高B型电脑销量,设计了旧电脑抵值活动:购买一台B型电脑时,可以用一台旧电脑抵值1000元.该中学计划只购买B型电脑,拿出的旧电脑和购买的B型电脑数量一共是30台.若要使购买B型电脑的数量是旧电脑数量的2倍,且购买B型电脑的实际总费用不少于100000元,则要在计划的基础上再多买a台B型电脑,此时该中学需要再拿出台的旧电脑参加抵值活动,求该中学至少需要再拿出多少台旧电脑进行抵值?
参考答案
一、选择题(本大题共10小题,每小题2分,共20分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.数学表达式①;②;③;④;⑤中不等式的个数是( )
A.个 B.个 C.个 D.个
【答案】C
【分析】根据不等式的定义(用符号“”或“”表示大小关系的式子,叫做不等式)逐个判断即可得.
【详解】解:①,②;⑤都是不等式,共有3个,
故选:C.
【点睛】本题考查了不等式的定义,熟记不等式的定义是解题关键.
2.下列说法错误的是( )
A.是不等式的解 B.是不等式的解
C.的解集是 D.的解集就是、、
【答案】D
【分析】根据不等式的性质即可求解.
【详解】解:A选项,是不等式的解,把代入不等式,不等式成立,故正确;
B选项,是不等式的解,把代入不等式,不等式成立,故正确;
C选项,的解集是,解不等式得,故正确;
D选项,的解集就是、、,不是不等式的解,故错误.
故选:D.
【点睛】本题主要考查不等式的性质解一元一次不等式,掌握不等式的性质是解题的关键.
3.设、为实数,则下列说法正确的是( )
A.,则 B.若,,则
C.若,,则 D.若,则
【答案】B
【分析】本题考查了不等式的性质“性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变;性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变;性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变”,熟练掌握不等式的性质是解题关键.根据不等式的性质逐项判断即可得.
【详解】解:A、若,则,不能确定,所以此项说法错误,不符合题意;
B、若,,则,所以,此项说法正确,符合题意;
C、若,,则,所以此项说法错误,不符合题意;
D、若,则或,所以不一定大于0,此项说法错误,不符合题意;
故选:B.
4.不等式组的解集在数轴上的表示正确的是( )
A. B.
C. D.
【答案】D
【分析】本题考查了解一元一次不等式组、在数轴上表示不等式组的解集,熟练掌握不等式组的解法是解题关键.先分别求出两个不等式的解集,再在数轴上表示不等式组的解集即可得.
【详解】解:,
解不等式①得:,
解不等式②得:,
在数轴上表示不等式组的解集如下:
故选:D.
5.下面是晓晓的一次数学课后作业,请帮助晓晓检查一下她的解题过程.
解不等式. 解:去分母,得. …………① 去括号,得. …………② 移项,得. …………③ 合并同类项,得. …………④ 系数化为1,得. …………⑤
晓晓的解题过程开始错误的一步是( )
A.① B.② C.③ D.④
【答案】A
【分析】此题考查了解一元一次不等式,根据解一元一次不等式的步骤求解即可得到答案.
【详解】解:.
去分母,得. …………①
去括号,得. …………②
移项,得. …………③
合并同类项,得. …………④
系数化为1,得. …………⑤
由解题过程可知,晓晓的解题过程开始错误的一步是①,
故选:A
6.已知不等式的解集是,则一次函数的图象可能是( )
A. B. C. D.
【答案】D
【分析】本题考查了一次函数的图象,解不等式,由不等式可得,进而由不等式的解集可得,,即得到一次函数的图象经过一、二、四象限,据此即可求解,由不等式的解集确定出的符号是解题的关键.
【详解】解:∵不等式,
∴,
∵不等式的解集是,
∴,,
∴一次函数的图象经过一、二、四象限,
故选:.
7.某商品进价为700元,出售时标价为1100元,后由于商品积压,商店准备打折销售,但要保证利润率不低于,则至多可打( )
A.六折 B.七折 C.八折 D.九折
【答案】B
【分析】设最多可打x折,根据题意,得,求整数解即可.
本题考查了一元一次不等式的应用,打折问题,正确理解,列出不等式解答是关键.
【详解】解:设最多可打x折,
根据题意,得,
解得.
故最多打7折,
故选B.
8.如图,在平面直角坐标系中,若直线与直线相交于点P,则下列结论正确的是( )
A.方程的解是
B.不等式和不等式的解集相同
C.不等式组的解集是
D.方程组的解是解为
【答案】C
【分析】本题考查一次函数的图象和性质.由图象可得直线与直线相交于点即可判断选项A;由图象可得的解集为,由图象可得的解集为,即可判断选项B;求出的解集是,当时,,即可判断选项C;由图象可得方程组的解为,即可判断选项D.
【详解】解:A.由图象可得直线与直线相交于点,
∴方程的解是,
故选项错误,不符合题意;
B.由图象可得的解集为,
由图象可得的解集为,
∴不等式和不等式的解集不相同,
故选项错误,不符合题意;
C.将代入得,
解得,
∴,
将代入得,
由图象可知,的解集是,
由图象可知,当时,直线在直线的下方,
∴当时,,
∴不等式组的解集是,
故选项正确,符合题意;
D.∵直线与直线相交于点P,
∴方程组的解为,
故选项错误,不符合题意.
故选:C.
9.某商店先后两次购买了某商品,第一次买了5件,平均价格为每件a元,第二次买了4件,平均价格为每件b元.后来商店以每件元的平均价格卖出,结果发现自己赔钱了,赔钱的原因是( )
A. B. C. D.
【答案】A
【分析】本题主要考查不等式的性质,解决问题的关键是读懂题意,找到关键描述语,联系实际,进而找到所求的量之间的不等关系.
首先表示9件商品的平均价格为 元,而以每件元的价格把商品全部卖掉,结果赔了钱,所以有,继而得出a和b的关系.
【详解】解:∵9件商品的平均价格为 元,
∵商店以每件元的平均价格卖出,结果发现自己赔钱了,
∴ ,
解得:,
故选:A.
10.关于x的不等式组有四个整数解,则a的取值范围是( )
A. B. C. D.
【答案】A
【分析】本题考查不等式组的解集,首先解出不等式的解集,再根据不等式组有且只有四个整数解,得到a的取值范围.
【详解】解:解不等式得,,
解不等式得,,
∵关于x的不等式组有四个整数解,而的四个整数是9,10,11,12,
∴,
解得,
∴a的取值范围是,
故选:A.
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.根据“a的3倍与2的差小于0”列出的不等式是: .
【答案】3a﹣2<0
【分析】关键描述语是:差小于0,应先算a的3倍,再算差.
【详解】根据题意,得3a﹣2<0.
故答案为:3a﹣2<0.
【点睛】本题考查了由实际问题抽象出一元一次不等式,读懂题意,抓住关键词语,弄清运算的先后顺序和不等关系,才能把文字语言的不等关系转化为用数学符号表示的不等式.
12.如果不等式的解集是,那么a必须满足 .
【答案】
【分析】根据两边同时除以a-2,不等号的方向改变,可得a-2<0.
【详解】解:∵不等式(a-2)x>a-2的解集是x<1,
∴a-2<0,
解得,a<2.
故答案为:a<2.
【点睛】本题考查了不等式的性质.注意:不等式两边同除以同一个负数时,不等号的方向改变.同理,当不等式两边同时除以一个数后不等号的方向改变,也可以知道不等式两边同时除以的是一个负数.
13.某商场计划购进甲、乙两种商品共100件.甲种商品每件进价15元,乙种商品每件进价35元,且购进两种商品的总费用不超过2700元,则购进甲种商品不少于 件.
【答案】40
【分析】本题考查不等式的实际应用,设购进甲种商品为件,根据购进两种商品的总费用不超过2700元,列出不等式进行求解即可.
【详解】解:设购进甲种商品为件,则购进乙种商品件,由题意,得:
,
解得:;
答:购进甲种商品不少于40件;
故答案为:40.
14.若关于x 的方程的解是负数,则m的取值范围是 .
【答案】
【分析】本题考查解一元一次方程、一元一次不等式,先解方程得,即可得,再求解即可.
【详解】解:,
去分母得,,
去括号得,,
∴,
∵原方程的解是负数,
∴,
解得,
故答案为:.
15.设表示x,y两个数中的最大值.例如“”.则关于x的函数的最小值为 .
【答案】/
【分析】本题主要考查一次函数的性质,根据题意正确画出图形并灵活运用数形结合是解答本题的关键.根据题意画出画在同一个坐标系中,再利用数形结合确定图形即可确定最小值.
【详解】解:如图:将画在同一个坐标系中,
令,
解得:,
则两条直线交点为,
当时,函数,最小值为;
当时,函数,最小值为;
综上,关于x的函数的最小值为,
故答案为:.
16.如图,钢架中,,焊上等长的钢条,,,…来加固钢架.若,且恰好用了根钢条,则的取值范围是 .
【答案】
【分析】此题考查了等腰三角形的性质,一元一次不等式组,以及三角形的外角性质,掌握以上知识点是解答本题的关键.
根据等腰三角形的性质可得到几组相等的角,再根据三角形外角的性质可得到与之间的关系,从而不难求解.
【详解】解:,,,,
,,,,
,
要使得这样的钢条恰好焊上根,
,
由题意得:,
,
故答案为:.
三、解答题(本大题共7小题,共62分.解答时应写出文字说明、证明过程或演算步骤)
17.解不等式(组):
(1);
(2),并把它的解集表示在数轴上.
【答案】(1)
(2),见解析
【分析】本题考查解一元一次不等式和解一元一次不等式组,正确求出每一个不等式的解集是基础,熟知几个不等式的解集的公共部分的找法是解题关键.
(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得解集;
(2)分别求出每一个不等式的解集,根据求不等式组解集的规律求出不等式组的解集,最后在数轴上表示出不等式组的解集即可.
【详解】(1)解:去括号,得,
移项得:,
合并同类项,得,
系数化为1,得.
(2)解不等式,得,
解不等式,得,
则不等式组的解集为.
将不等式组的解集表示在数轴上如下:
18.如图,这是某大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,若第x个所贴“○”的个数为y.
(1)填写下表:
x 1 2 3 4 5 … x
y 5 8 ______ … ______(用含x的式子表示)
(2)若第x个所贴“○”的个数为,求x的值;
(3)若第x个所贴的“○”的个数大于,求x的取值范围.
【答案】(1),
(2)
(3)
【分析】(1)根据图形规律可得,;,,,,进而得出答案;
(2)根据(1)中得出的规律列出方程,求解即可;
(3)根据(1)中的结论列出不等式,求解即可.
【详解】(1)解:根据题意:,;
,;
,;
,;
∴;
故答案为:,;
(2)根据题意可得:,
解得:;
(3)根据题意可得:,
解得:.
【点睛】本题考查了图形的变化规律,一元一次方程的应用,一元一次不等式的应用,读懂题意,得出图形的变化规律是解本题的关键.
19.定义关于的一种运算:,如.
(1)若,求的取值范围.
(2)若关于的不等式的解和的解相同,求的值.
【答案】(1)
(2)
【分析】()根据新定义运算列出不等式即可求解;
()分别求出两个不等式的解集,再根据解集相同即可求解;
本题考查了新定义,解一元一次不等式,理解新定义是解题的关键.
【详解】(1)解:由题意得,,
∴,
∴;
(2)解:解不等式得,,
由得,,
∴,
∵不等式的解和的解相同,
∴,
解得.
20.已知方程组的解满足x为非正数,y为负数.
(1)求m得取值范围.
(2)在m的取值范围内,当m为何整数时,不等式的解为.
【答案】(1)
(2)
【分析】本题主要考查了解二元一次方程组,求一元一次不等式组的整数解,根据不等式的解集求参数:
(1)先利用加减消元法求出方程组的解为,进而得到,解不等式组即可得到答案;
(2)先把原不等式变形为,根据解集为得到,进而求出,据此可得答案.
【详解】(1)解:
得:,解得,
把代入①得:,解得,
∴方程组的解为,
∵x为非正数,y为负数,
∴,,
∴,
解得,
∴m的取值范围是.
(2)解:将不等式整理,得,
∵其解集为,
∴,
解得
∴.
结合m取整数,可得,
即当时,不等式的解集为.
21.如图,在平面直角坐标系中,一次函数(、为常数且)的图象经过点,且与正比例函数的图象交于点.
(1)求的值及一次函数的表达式;
(2)关于的不等式的解集为 ;
(3)直线上存在点,满足的面积是的面积倍,则点的坐标为 .
【答案】(1),;
(2);
(3)或.
【分析】本题考出来一次函数与一元一次不等式的关系,掌握待定系数法、三角形面积公式及数形结合思想是解题的关键.
(1)根据待定系数法求解;
(2)根据数形结合思想求解;
(3)根据三角形的面积公式求解.
【详解】(1)解:由题意得:,
解得,
,
解得:
一次函数的表达式为:;
(2)解:由图象得,当时,,
故答案为;
(3)解:设,
由题意得:,
解得:或,
或,
或,
故答案为:或.
22.如图,在中,,射线,点从点出发沿射线以的速度运动,当点出发后,点也从点出发沿射线以的速度运动,分别连接,,.设点运动时间为,其中.
(1)若,则的取值范围是______;
(2)求为何值时,平分的面积;
(3)求为何值时,.
【答案】(1)
(2)2.5秒
(3)秒或12秒
【分析】(1)根据当时,点F在线段上运动可得答案;
(2)根据当平分的面积时,点F是线段的中点可得答案;
(3)分类讨论:当点F在点C左侧时,点F再点C的右侧时,可得关于t的一元一次方程,根据解方程,可得答案;
【详解】(1)当时,,
∴,
解得,
故答案为:;
(2)∵平分的面积,
∴,
∴,
∴;
(3)分两种情况讨论:
①点F在点C左侧时,,
则,
解得;
②当点F在点C的右侧时,,
则,
解得,
综上所述,或12时,;
【点睛】本题考查了一元一次不等式的应用,一元一次方程的应用,三角形中线的性质,数形结合是解答本题的关键.
23.一家电脑公司有A型、B型、C型三种型号的电脑,其中A型每台6000元、B型每台4000元、C型每台2500元.某中学计划从这家电脑公司购进电脑.
(1)若该中学只购买A型电脑和B型电脑,且购买A型电脑的数量比购买B型电脑的数量的一半还少1台,要求购买的总价不超过90000元,则最多可以购买多少台A型电脑?
(2)若该中学现有专项资金100500元,计划从这家电脑公司购进36台两种型号的电脑,且这笔资金恰好全用完.请你设计几种不同的购买方案供这个学校选择,并说明理由.
(3)这家电脑公司为提高B型电脑销量,设计了旧电脑抵值活动:购买一台B型电脑时,可以用一台旧电脑抵值1000元.该中学计划只购买B型电脑,拿出的旧电脑和购买的B型电脑数量一共是30台.若要使购买B型电脑的数量是旧电脑数量的2倍,且购买B型电脑的实际总费用不少于100000元,则要在计划的基础上再多买a台B型电脑,此时该中学需要再拿出台的旧电脑参加抵值活动,求该中学至少需要再拿出多少台旧电脑进行抵值?
【答案】(1)最多可以购买5台A型电脑
(2)有两种方案供这个学校选择:第一种方案是购进A型电脑3台、C型电脑33台;第二种方案是购进B型电脑7台、C型电脑29台
(3)该中学至少需要再拿出4台旧电脑进行抵值
【分析】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程组;(3)根据各数量之间的关系,正确列出一元一次不等式.
(1)设购买台型电脑,则购买台型电脑,利用总价单价数量,结合总价不超过90000元,可列出关于的一元一次不等式,解之可得出的取值范围,再结合,均为正整数,即可找出的最大值;
(2)利用平均价格总价单价,可求出平均价格,结合,,三种型号电脑的单价,可得出可能有两种情况,①购买型电脑和型电脑,设购买台型电脑,台型电脑,利用总价单价数量,结合用100500元购买36台两种型号的电脑,可列出关于,的二元一次方程组,解之可得出结论;②购买型电脑和型电脑,设购买台型电脑,台型电脑,利用总价单价数量,结合用100500元购买36台两种型号的电脑,可列出关于,的二元一次方程组,解之可得出结论;
(3)设原计划购买台型电脑,则原计划拿出台旧电脑,根据购买型电脑的数量是旧电脑数量的2倍,可列出关于,的二元一次方程,变形后可得出,利用总价单价数量,结合购买型电脑的实际总费用不少于100000元,可列出关于的一元一次不等式,解之可得出的取值范围,再结合,均为正整数,即可找出的最小值为6.
【详解】(1)解:设购买台型电脑,则购买台型电脑,
根据题意得:,
解得:,
,均为正整数,
的最大值为12,的最大值为5.
答:最多可以购买5台型电脑;
(2)解:共有2种购买方案,
方案1:购买3台型电脑,33台型电脑;
方案2:购买7台型电脑,29台型电脑,理由如下:
(元,,
可能有两种情况.
①购买型电脑和型电脑,设购买台型电脑,台型电脑,
根据题意得:,
解得:,
购买3台型电脑,33台型电脑;
②购买型电脑和型电脑,设购买台型电脑,台型电脑,
根据题意得:,
解得:,
购买7台型电脑,29台型电脑.
共有2种购买方案,
方案1:购买3台型电脑,33台型电脑;
方案2:购买7台型电脑,29台型电脑;
(3)解:设原计划购买台型电脑,则原计划拿出台旧电脑,
根据题意得:,
.
购买型电脑的实际总费用不少于100000元,
,
即,
解得:,
.
答:该中学至少需要再拿出4台旧电脑进行抵值.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
