北师大版小学数学六年级下册第一单元综合素养测评B卷(含答案)
文档属性
| 名称 | 北师大版小学数学六年级下册第一单元综合素养测评B卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 731.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 13:35:45 | ||
图片预览


文档简介
第一单元综合素养测评 B卷
素养形成与创新
时间:90分钟 满分:100分+10分
一、填空。(每空1分,共15分)
1.《西游记》中,孙悟空的如意金箍棒的形状是一个圆柱,孙悟空拿在手上时的长度约为6.7 m。若它的体积约为0.1 m3 ,则它的底面积约为( ) m2 。(结果保留两位小数)
2.如图,一个立体图形从正面看到的是图形 ,从上面看到的是图形 ,这个立体图形的体积是( ) cm3 。
如果用一个长方体(或正方体) 盒子包装它,那么这个盒子的容积至少是( ) mL 。
3.将一张长75.36 cm、宽62.8 cm 的长方形铁皮卷成一个圆柱形垃
圾桶的侧面,给这个垃圾桶配一个底面,至少还需要( ) cm2 的铁皮。
4.把一根长2 m 的圆柱形木料截成3段小圆柱后,表面积增加了12 dm2,则原来这根木料的体积是( ) m3 。
5.把一个棱长为6 cm的正方体钢坯熔铸成一个底面积是54 cm2 的圆锥,这个圆锥的高是( ) cm ;如果将这个正方体钢坯削成一个最大的圆柱,那么这个圆柱的体积是( ) cm3 。
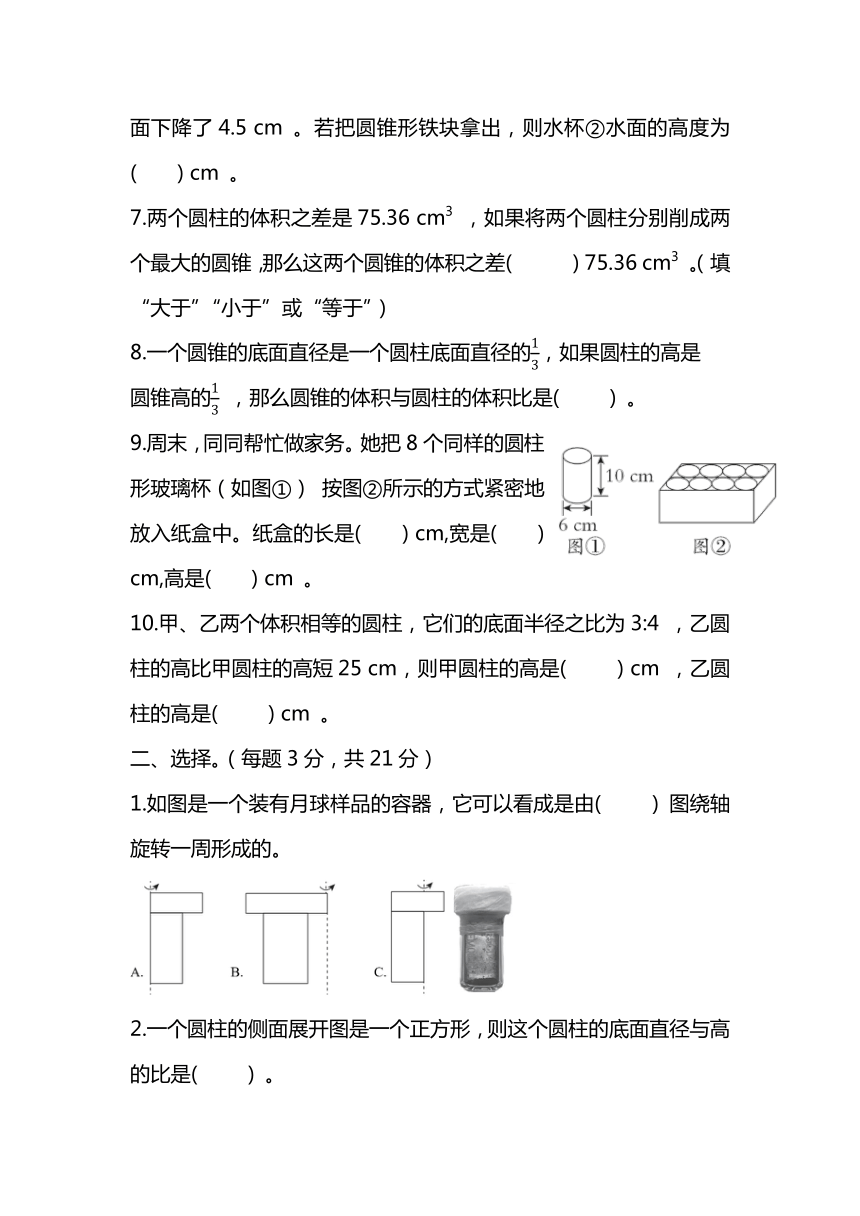
6.如图,两个大小相同的水杯中分别放入等底等高的圆柱形和圆锥形铁块,这时两个水杯的水深都为10 cm ,把圆柱形铁块拿出后,水杯①水面下降了4.5 cm 。若把圆锥形铁块拿出,则水杯②水面的高度为 ( ) cm 。
7.两个圆柱的体积之差是75.36 cm3 ,如果将两个圆柱分别削成两个最大的圆锥,那么这两个圆锥的体积之差( ) 75.36 cm3 。(填“大于”“小于”或“等于”)
8.一个圆锥的底面直径是一个圆柱底面直径的,如果圆柱的高是
圆锥高的 ,那么圆锥的体积与圆柱的体积比是( ) 。
9.周末,同同帮忙做家务。她把8个同样的圆柱形玻璃杯(如图①) 按图②所示的方式紧密地放入纸盒中。纸盒的长是( ) cm,宽是( ) cm,高是( ) cm 。
10.甲、乙两个体积相等的圆柱,它们的底面半径之比为3:4 ,乙圆柱的高比甲圆柱的高短25 cm,则甲圆柱的高是( ) cm ,乙圆柱的高是( ) cm 。
二、选择。(每题3分,共21分)
1.如图是一个装有月球样品的容器,它可以看成是由( ) 图绕轴旋转一周形成的。
2.一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面直径与高的比是( ) 。
A.1:2π B.1:π C.2:π D.2π:1
3.如图,两个三角形绕同一条轴旋转一周,涂色三角形与空白三角形所形成的立体图形的体积比是( ) 。
A.1:1 B.1:2 C.1:3 D.2:3
4.一个圆柱与一个圆锥的底面半径之比是2:3,高之比是3:2 ,则圆柱的体积与圆锥的体积之比是( ) 。
A.1:1 B.2:1 C.3:1 D.9:2
5. 《九章算术》是我国古代的一部数学名著,书中记载的圆柱体积的计算方法为“周自相乘,以高乘之,十二而一”,意思是圆柱的体积=×底面周长的平方×高。结合我们学过的圆柱体积的计算公式,该计算方法中圆周率的取值为( ) 。
A.3.14 B.3.1 C.3 D.3.1415926
6.如图,圆柱形容器的底面半径为10 cm,水的高度为12 cm ,水中浸没着一个底面半径为4 cm 的圆锥形铅锤,把铅锤从水中取出后,水面下降了0.7 cm 。根据以上信息,不能解决的问题是( ) 。(容器的厚度忽略不计)
A.容器内装了多少升水 B.铅锤的体积是多少立方厘米
C.铅锤的高是多少厘米 D.容器的高是多少厘米
7.用下列各图中的阴影部分都可以做成一个圆柱,其中圆柱侧面积是100.48 cm2 的是( ) 。
三、计算。(共16分)
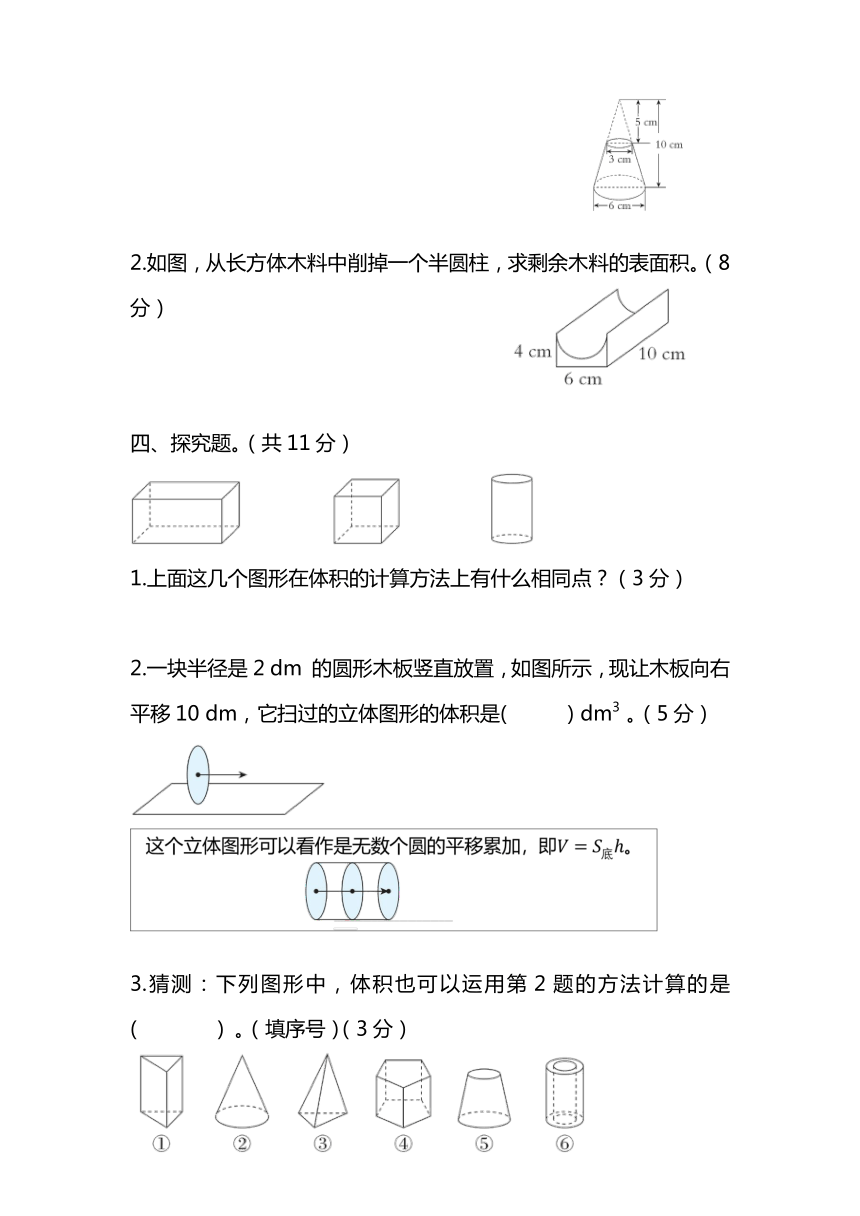
1.求下面零件的体积。(8分)
2.如图,从长方体木料中削掉一个半圆柱,求剩余木料的表面积。(8分)
四、探究题。(共11分)
1.上面这几个图形在体积的计算方法上有什么相同点?(3分)
2.一块半径是2 dm 的圆形木板竖直放置,如图所示,现让木板向右平移10 dm,它扫过的立体图形的体积是( ) dm3 。(5分)
3.猜测:下列图形中,体积也可以运用第2题的方法计算的是( ) 。(填序号)(3分)
五、解决问题。(共37分)
1.一个无盖的圆柱形水桶,底面直径是2 dm,高是3 dm ,制作这样一个水桶至少需要多少平方分米的铁皮?若水桶装满水后再放入一个和圆柱形水桶等底等高的圆锥形铁块,则水会溢出多少升?(铁皮厚度和接头处忽略不计)(7分)
2. 有一个圆锥形容器装满了200 mL 香油,小老鼠偷偷在容器的正中间咬了一个洞偷油,一直偷到油面与洞口齐平为止(如图) ,此时油面直径是容器底面直径的1/2 ,小老鼠共偷了多少毫升香油 (容器厚度忽略不计)
1)油面的半径与容器底面半径的比是( ) ,油面的高度与容器高度的比是( ) ,则剩余香油的体积与容器容积的比是( ) 。(3分)
(2)列式求出小老鼠共偷了多少毫升香油。(5分)
3.《九章算术》是我国古代数学著作,书中提到:“今有委米依垣内角,下周八尺,高五尺。”其意思是:在屋内墙角处堆放米(如图,米堆
为一个圆锥的四分之一) ,米堆底部的弧长为8尺,米堆的高为
5尺。已知1斛米的体积约为1.62立方尺,则堆放的米约有多少斛?
(结果保留整数)(π 取3) (7分)
4.某学校举办操作技能比赛,要求把完全一样的圆柱形橡皮平均切割成相同的两块,且切成的不是圆柱。如图所示为典典和天天按要求切去一半后的形状,原来圆柱形橡皮的体积是多少立方厘米?(7分)
5.在一节数学活动课上,同学们进行实践操作,先往一个长方体的容
器中注水,水深4.4 cm (如图①) 然后将一根圆柱形冰柱垂直放入其中,水面的高度上升到5.5 cm,这时刚好有 的冰柱浸没在水中(如图②) 。整根冰柱的体积是多少立方厘米?(8分)
挑战题: 天才的你,试一试。(10分)
下图是一个由圆柱和圆锥组成的容器,圆柱的高是7 cm ,圆锥的高是3 cm,容器内的水深是5 cm 。将这个容器倒过来放时,从圆锥的尖端到水面的高度是多少?
参考答案
一、1. 0.01
2. 56.52 216
3.314
4. 0.06
5.12 169.56
6.8.5
7. 小于
8. 1:9
9.24 12 10
10.
二、1.A 2.B 3.B 4.B 5.C 6.D 7.B
三、1.
2.
四、1. 它们的体积都等于底面积×高。
2.125.6
3. ①④⑥
五、1.
2.(1)1:2 1:2 1:8
(2)200÷8×(8 1)=175(mL)
答:小老鼠共偷了175 mL 香油。
3.
4.
5.
挑战题:3÷3=1(cm) 3+(5 1)=7(cm)
答:从圆锥的尖端到水面的高度是7 cm 。
解析:根据等底等高的圆柱的体积是圆锥体积的3倍,先把圆
柱内高为3 cm的水的体积的1/3,即高为1 cm 的水的体积倒入圆锥
中,正好把圆锥部分装满,则剩下的就是圆柱内水的高度,即
5 1=4(cm),由圆锥的高度+ 剩下的圆柱内水的高度即可解决
问题。
素养形成与创新
时间:90分钟 满分:100分+10分
一、填空。(每空1分,共15分)
1.《西游记》中,孙悟空的如意金箍棒的形状是一个圆柱,孙悟空拿在手上时的长度约为6.7 m。若它的体积约为0.1 m3 ,则它的底面积约为( ) m2 。(结果保留两位小数)
2.如图,一个立体图形从正面看到的是图形 ,从上面看到的是图形 ,这个立体图形的体积是( ) cm3 。
如果用一个长方体(或正方体) 盒子包装它,那么这个盒子的容积至少是( ) mL 。
3.将一张长75.36 cm、宽62.8 cm 的长方形铁皮卷成一个圆柱形垃
圾桶的侧面,给这个垃圾桶配一个底面,至少还需要( ) cm2 的铁皮。
4.把一根长2 m 的圆柱形木料截成3段小圆柱后,表面积增加了12 dm2,则原来这根木料的体积是( ) m3 。
5.把一个棱长为6 cm的正方体钢坯熔铸成一个底面积是54 cm2 的圆锥,这个圆锥的高是( ) cm ;如果将这个正方体钢坯削成一个最大的圆柱,那么这个圆柱的体积是( ) cm3 。
6.如图,两个大小相同的水杯中分别放入等底等高的圆柱形和圆锥形铁块,这时两个水杯的水深都为10 cm ,把圆柱形铁块拿出后,水杯①水面下降了4.5 cm 。若把圆锥形铁块拿出,则水杯②水面的高度为 ( ) cm 。
7.两个圆柱的体积之差是75.36 cm3 ,如果将两个圆柱分别削成两个最大的圆锥,那么这两个圆锥的体积之差( ) 75.36 cm3 。(填“大于”“小于”或“等于”)
8.一个圆锥的底面直径是一个圆柱底面直径的,如果圆柱的高是
圆锥高的 ,那么圆锥的体积与圆柱的体积比是( ) 。
9.周末,同同帮忙做家务。她把8个同样的圆柱形玻璃杯(如图①) 按图②所示的方式紧密地放入纸盒中。纸盒的长是( ) cm,宽是( ) cm,高是( ) cm 。
10.甲、乙两个体积相等的圆柱,它们的底面半径之比为3:4 ,乙圆柱的高比甲圆柱的高短25 cm,则甲圆柱的高是( ) cm ,乙圆柱的高是( ) cm 。
二、选择。(每题3分,共21分)
1.如图是一个装有月球样品的容器,它可以看成是由( ) 图绕轴旋转一周形成的。
2.一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面直径与高的比是( ) 。
A.1:2π B.1:π C.2:π D.2π:1
3.如图,两个三角形绕同一条轴旋转一周,涂色三角形与空白三角形所形成的立体图形的体积比是( ) 。
A.1:1 B.1:2 C.1:3 D.2:3
4.一个圆柱与一个圆锥的底面半径之比是2:3,高之比是3:2 ,则圆柱的体积与圆锥的体积之比是( ) 。
A.1:1 B.2:1 C.3:1 D.9:2
5. 《九章算术》是我国古代的一部数学名著,书中记载的圆柱体积的计算方法为“周自相乘,以高乘之,十二而一”,意思是圆柱的体积=×底面周长的平方×高。结合我们学过的圆柱体积的计算公式,该计算方法中圆周率的取值为( ) 。
A.3.14 B.3.1 C.3 D.3.1415926
6.如图,圆柱形容器的底面半径为10 cm,水的高度为12 cm ,水中浸没着一个底面半径为4 cm 的圆锥形铅锤,把铅锤从水中取出后,水面下降了0.7 cm 。根据以上信息,不能解决的问题是( ) 。(容器的厚度忽略不计)
A.容器内装了多少升水 B.铅锤的体积是多少立方厘米
C.铅锤的高是多少厘米 D.容器的高是多少厘米
7.用下列各图中的阴影部分都可以做成一个圆柱,其中圆柱侧面积是100.48 cm2 的是( ) 。
三、计算。(共16分)
1.求下面零件的体积。(8分)
2.如图,从长方体木料中削掉一个半圆柱,求剩余木料的表面积。(8分)
四、探究题。(共11分)
1.上面这几个图形在体积的计算方法上有什么相同点?(3分)
2.一块半径是2 dm 的圆形木板竖直放置,如图所示,现让木板向右平移10 dm,它扫过的立体图形的体积是( ) dm3 。(5分)
3.猜测:下列图形中,体积也可以运用第2题的方法计算的是( ) 。(填序号)(3分)
五、解决问题。(共37分)
1.一个无盖的圆柱形水桶,底面直径是2 dm,高是3 dm ,制作这样一个水桶至少需要多少平方分米的铁皮?若水桶装满水后再放入一个和圆柱形水桶等底等高的圆锥形铁块,则水会溢出多少升?(铁皮厚度和接头处忽略不计)(7分)
2. 有一个圆锥形容器装满了200 mL 香油,小老鼠偷偷在容器的正中间咬了一个洞偷油,一直偷到油面与洞口齐平为止(如图) ,此时油面直径是容器底面直径的1/2 ,小老鼠共偷了多少毫升香油 (容器厚度忽略不计)
1)油面的半径与容器底面半径的比是( ) ,油面的高度与容器高度的比是( ) ,则剩余香油的体积与容器容积的比是( ) 。(3分)
(2)列式求出小老鼠共偷了多少毫升香油。(5分)
3.《九章算术》是我国古代数学著作,书中提到:“今有委米依垣内角,下周八尺,高五尺。”其意思是:在屋内墙角处堆放米(如图,米堆
为一个圆锥的四分之一) ,米堆底部的弧长为8尺,米堆的高为
5尺。已知1斛米的体积约为1.62立方尺,则堆放的米约有多少斛?
(结果保留整数)(π 取3) (7分)
4.某学校举办操作技能比赛,要求把完全一样的圆柱形橡皮平均切割成相同的两块,且切成的不是圆柱。如图所示为典典和天天按要求切去一半后的形状,原来圆柱形橡皮的体积是多少立方厘米?(7分)
5.在一节数学活动课上,同学们进行实践操作,先往一个长方体的容
器中注水,水深4.4 cm (如图①) 然后将一根圆柱形冰柱垂直放入其中,水面的高度上升到5.5 cm,这时刚好有 的冰柱浸没在水中(如图②) 。整根冰柱的体积是多少立方厘米?(8分)
挑战题: 天才的你,试一试。(10分)
下图是一个由圆柱和圆锥组成的容器,圆柱的高是7 cm ,圆锥的高是3 cm,容器内的水深是5 cm 。将这个容器倒过来放时,从圆锥的尖端到水面的高度是多少?
参考答案
一、1. 0.01
2. 56.52 216
3.314
4. 0.06
5.12 169.56
6.8.5
7. 小于
8. 1:9
9.24 12 10
10.
二、1.A 2.B 3.B 4.B 5.C 6.D 7.B
三、1.
2.
四、1. 它们的体积都等于底面积×高。
2.125.6
3. ①④⑥
五、1.
2.(1)1:2 1:2 1:8
(2)200÷8×(8 1)=175(mL)
答:小老鼠共偷了175 mL 香油。
3.
4.
5.
挑战题:3÷3=1(cm) 3+(5 1)=7(cm)
答:从圆锥的尖端到水面的高度是7 cm 。
解析:根据等底等高的圆柱的体积是圆锥体积的3倍,先把圆
柱内高为3 cm的水的体积的1/3,即高为1 cm 的水的体积倒入圆锥
中,正好把圆锥部分装满,则剩下的就是圆柱内水的高度,即
5 1=4(cm),由圆锥的高度+ 剩下的圆柱内水的高度即可解决
问题。
