1.2整式的乘法(2)课件(32张PPT)北师版数学七年级下册
文档属性
| 名称 | 1.2整式的乘法(2)课件(32张PPT)北师版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 12:32:08 | ||
图片预览









文档简介
(共32张PPT)
2024-2025学年北师版数学
七年级(上册)
学习·目标
1.能根据乘法分配律和单项式与单项式相乘的法则,探究单项式与多项式相乘的法则; (重点)
2.掌握单项式与多项式相乘的法则并会运用; (难点)
3.理解并掌握多项式与多项式的乘法运算法则;(重点)
4.能够用多项式与多项式的乘法运算法则进行计算。(难点)
回顾 ·思考
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式。
1.单项式与单项式的乘法法则
在多项式中,每个单项式叫作多项式的项。
2.什么叫多项式的项
请说出多项式3x2+2x+5的项和各项系数。
情境·导入
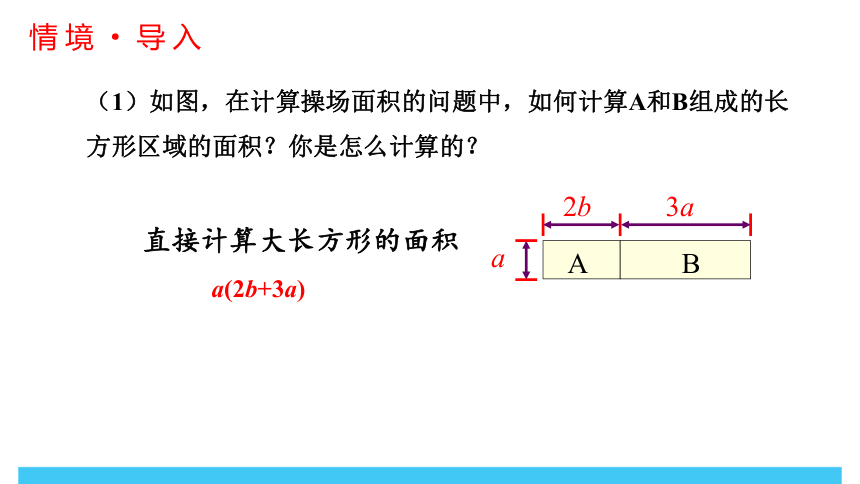
(1)如图,在计算操场面积的问题中,如何计算A和B组成的长方形区域的面积?你是怎么计算的?
直接计算大长方形的面积
a(2b+3a)
2b
3a
a
A B
情境·导入
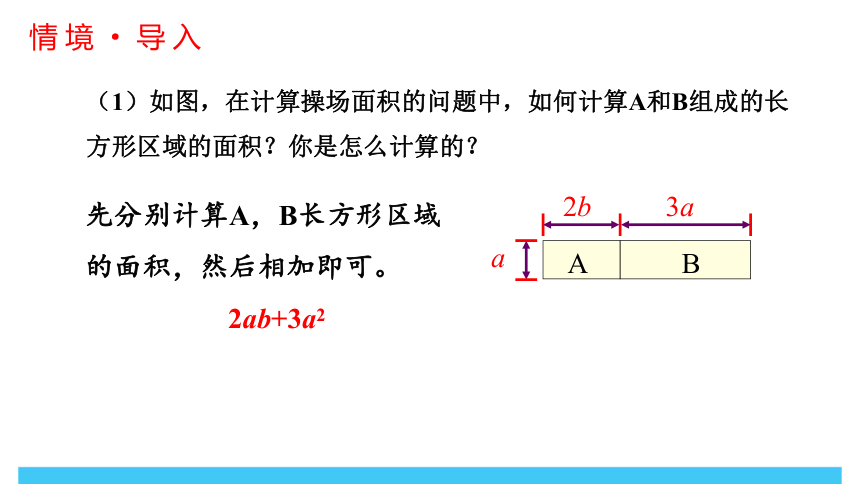
(1)如图,在计算操场面积的问题中,如何计算A和B组成的长方形区域的面积?你是怎么计算的?
2b
3a
a
A B
先分别计算A,B长方形区域
的面积,然后相加即可。
2ab+3a2
情境·导入
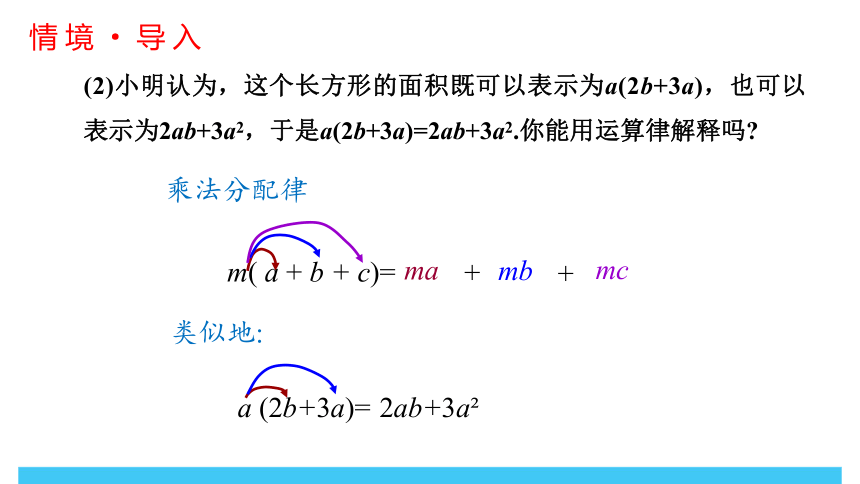
(2)小明认为,这个长方形的面积既可以表示为a(2b+3a),也可以表示为2ab+3a2,于是a(2b+3a)=2ab+3a2.你能用运算律解释吗
m( a + b + c)=
ma
mb
mc
+
+
a (2b+3a)=
2ab+3a
类似地:
乘法分配律
操作·交流
(1)你能计算 ab·(abc+2x),c2·(m+n-p),(x2y+xy2)·(-xy)吗
ab·(abc+2x)=ab·abc+ab·2x =a2b2c+2xab,
c2·(m+n-p)=c2m+c2n-c2p,
(x2y+xy2)·(-xy)=x2y·(-xy)+xy2·(-xy)=-x3y2-x2y3。
操作·交流
(2)一般地,如何进行单项式乘多项式的运算?
解:原式
单项式乘以单项式
单项式乘以多项式
转化
=2x·x+2x·2y
=2x2+4xy
2x(x+2y)
单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加。
单项式与多项式的乘法法则:
注意:(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同。
用字母表示:
p(a+b+c)=pa+pb+pc
总结:
单项式与多项式相乘时,依据法则将其转化为单项式与单项式相乘,积与积之间用“+”号相连,然后按单项式与单项式相乘的法则逐个计算,特别要注意符号。
例 计算:
(1) 2ab(5ab2+3a2b); (2) (ab2-2ab)·ab;
(3) 5m2n(2n+3m-n2); (4) 2(x+y2z+xy2z3)·xyz。
解:(1) 2ab(5ab2+3a2b)
=2ab·5ab2+2ab·3a2b
=10a2b3+6a3b2;
(2) (ab2-2ab)·ab
=ab2·ab+(-2ab)·ab
=a2b3-a2b2;
例 计算:
(1) 2ab(5ab2+3a2b); (2) (ab2-2ab)·ab;
(3) 5m2n(2n+3m-n2); (4) 2(x+y2z+xy2z3)·xyz。
解:(3) 5m2n(2n+3m-n2)
=5m2n·2n+5m2n·3m+5m2n·(-n2)
=10m2n2+15m3n-5m2n3;
(4) 2(x+y2z+xy2z3)·xyz
= (2x+2y2z+2xy2z3)·xyz
= 2x·xyz +2y2z·xyz +2xy2z3·xyz
= 2x2yz +2xy3z2 +2x2y3z4。
尝试·交流
(1)如何计算(2a+b)(a+2b),(x+y)(x-1),(a2-b2)(a-b)?你是怎么做的?
(2a+b)(a+2b)=2a(a+2b)+b(a+2b)
=2a2+4ab+ab+2b2
=2a2+5ab +2b2;
(a2-b2)(a-b)=(a2-b2)a-(a2-b2)b
=a3-ab2-a2b+b3。
(x+y)(x-1)=(x+y)x-(x+y)
=x2+xy-x-y;
尝试·交流
(2)一般地,如何进行多项式乘多项式的运算?与同伴进行交流。
多项式与多项式的乘法法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
用字母表示:
(a+b)(m+n)=am+an+bm+bn
例 计算:(1) (1-x) (0.6-x); (2) (2x + y) (x-y)。
解:(1) 原式=1×0.6-1· x-x·0.6 + x·x
=0.6-x-0.6x+ x2
=0.6-1.6x+ x2;
(2) 原式=2x·x-2x·y + y·x-y·y
=2x2-2xy+xy-y2
=2x2-xy-y2。
需要注意的几个问题:
(1)不要漏乘;
(2)符号问题;
(3)最后结果应化成最简形式。
(1)如图,一幅边长为a m的正方形风景画,左右各留有宽为x m的长方形空白区域作装饰,中间画面的面积是多少平方米
(1) a·(a - x - x)
=a·(a - x)
=a·a-a·x
=(a2-ax) m2。
x
a
x
观察·思考
(2)如图,一幅长为a m、宽为b m的长方形风景画,画面的四周留有空白区域作装饰,其中四角均是边长为x m的正方形,正中间画面的面积是多少平方米
(2) (a-2x)(b-2x)
=(ab-2ax-2bx+4x2) m2。
x
b
a
x
观察·思考
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
单项式乘以多项式
1.注意运算顺序和每一项的符号
2.不要漏乘
3.结果应仍是多项式,且项数与计算前相同
乘法分配律
依据
注意
法则
单项式与多项式相乘,就是根据分配律用单项式乘多项式的每一项,再把所得的积相加,即a(m+n)=am+an
小结·反思
小结·反思
多项式乘以多项式
结果中的同类项要合并
注意运算顺序和每一项的符号
不要漏乘
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加
(a+b)(m+n)=am+an+bm+bn
注意
法则
2024-2025学年北师版数学
七年级(上册)
学习·目标
1.能根据乘法分配律和单项式与单项式相乘的法则,探究单项式与多项式相乘的法则; (重点)
2.掌握单项式与多项式相乘的法则并会运用; (难点)
3.理解并掌握多项式与多项式的乘法运算法则;(重点)
4.能够用多项式与多项式的乘法运算法则进行计算。(难点)
回顾 ·思考
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式。
1.单项式与单项式的乘法法则
在多项式中,每个单项式叫作多项式的项。
2.什么叫多项式的项
请说出多项式3x2+2x+5的项和各项系数。
情境·导入
(1)如图,在计算操场面积的问题中,如何计算A和B组成的长方形区域的面积?你是怎么计算的?
直接计算大长方形的面积
a(2b+3a)
2b
3a
a
A B
情境·导入
(1)如图,在计算操场面积的问题中,如何计算A和B组成的长方形区域的面积?你是怎么计算的?
2b
3a
a
A B
先分别计算A,B长方形区域
的面积,然后相加即可。
2ab+3a2
情境·导入
(2)小明认为,这个长方形的面积既可以表示为a(2b+3a),也可以表示为2ab+3a2,于是a(2b+3a)=2ab+3a2.你能用运算律解释吗
m( a + b + c)=
ma
mb
mc
+
+
a (2b+3a)=
2ab+3a
类似地:
乘法分配律
操作·交流
(1)你能计算 ab·(abc+2x),c2·(m+n-p),(x2y+xy2)·(-xy)吗
ab·(abc+2x)=ab·abc+ab·2x =a2b2c+2xab,
c2·(m+n-p)=c2m+c2n-c2p,
(x2y+xy2)·(-xy)=x2y·(-xy)+xy2·(-xy)=-x3y2-x2y3。
操作·交流
(2)一般地,如何进行单项式乘多项式的运算?
解:原式
单项式乘以单项式
单项式乘以多项式
转化
=2x·x+2x·2y
=2x2+4xy
2x(x+2y)
单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加。
单项式与多项式的乘法法则:
注意:(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同。
用字母表示:
p(a+b+c)=pa+pb+pc
总结:
单项式与多项式相乘时,依据法则将其转化为单项式与单项式相乘,积与积之间用“+”号相连,然后按单项式与单项式相乘的法则逐个计算,特别要注意符号。
例 计算:
(1) 2ab(5ab2+3a2b); (2) (ab2-2ab)·ab;
(3) 5m2n(2n+3m-n2); (4) 2(x+y2z+xy2z3)·xyz。
解:(1) 2ab(5ab2+3a2b)
=2ab·5ab2+2ab·3a2b
=10a2b3+6a3b2;
(2) (ab2-2ab)·ab
=ab2·ab+(-2ab)·ab
=a2b3-a2b2;
例 计算:
(1) 2ab(5ab2+3a2b); (2) (ab2-2ab)·ab;
(3) 5m2n(2n+3m-n2); (4) 2(x+y2z+xy2z3)·xyz。
解:(3) 5m2n(2n+3m-n2)
=5m2n·2n+5m2n·3m+5m2n·(-n2)
=10m2n2+15m3n-5m2n3;
(4) 2(x+y2z+xy2z3)·xyz
= (2x+2y2z+2xy2z3)·xyz
= 2x·xyz +2y2z·xyz +2xy2z3·xyz
= 2x2yz +2xy3z2 +2x2y3z4。
尝试·交流
(1)如何计算(2a+b)(a+2b),(x+y)(x-1),(a2-b2)(a-b)?你是怎么做的?
(2a+b)(a+2b)=2a(a+2b)+b(a+2b)
=2a2+4ab+ab+2b2
=2a2+5ab +2b2;
(a2-b2)(a-b)=(a2-b2)a-(a2-b2)b
=a3-ab2-a2b+b3。
(x+y)(x-1)=(x+y)x-(x+y)
=x2+xy-x-y;
尝试·交流
(2)一般地,如何进行多项式乘多项式的运算?与同伴进行交流。
多项式与多项式的乘法法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
用字母表示:
(a+b)(m+n)=am+an+bm+bn
例 计算:(1) (1-x) (0.6-x); (2) (2x + y) (x-y)。
解:(1) 原式=1×0.6-1· x-x·0.6 + x·x
=0.6-x-0.6x+ x2
=0.6-1.6x+ x2;
(2) 原式=2x·x-2x·y + y·x-y·y
=2x2-2xy+xy-y2
=2x2-xy-y2。
需要注意的几个问题:
(1)不要漏乘;
(2)符号问题;
(3)最后结果应化成最简形式。
(1)如图,一幅边长为a m的正方形风景画,左右各留有宽为x m的长方形空白区域作装饰,中间画面的面积是多少平方米
(1) a·(a - x - x)
=a·(a - x)
=a·a-a·x
=(a2-ax) m2。
x
a
x
观察·思考
(2)如图,一幅长为a m、宽为b m的长方形风景画,画面的四周留有空白区域作装饰,其中四角均是边长为x m的正方形,正中间画面的面积是多少平方米
(2) (a-2x)(b-2x)
=(ab-2ax-2bx+4x2) m2。
x
b
a
x
观察·思考
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
典例讲解
单项式乘以多项式
1.注意运算顺序和每一项的符号
2.不要漏乘
3.结果应仍是多项式,且项数与计算前相同
乘法分配律
依据
注意
法则
单项式与多项式相乘,就是根据分配律用单项式乘多项式的每一项,再把所得的积相加,即a(m+n)=am+an
小结·反思
小结·反思
多项式乘以多项式
结果中的同类项要合并
注意运算顺序和每一项的符号
不要漏乘
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加
(a+b)(m+n)=am+an+bm+bn
注意
法则
同课章节目录
