第17章 勾股定理 培优提能测试题(含答案)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 第17章 勾股定理 培优提能测试题(含答案)2024-2025学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 19:04:40 | ||
图片预览


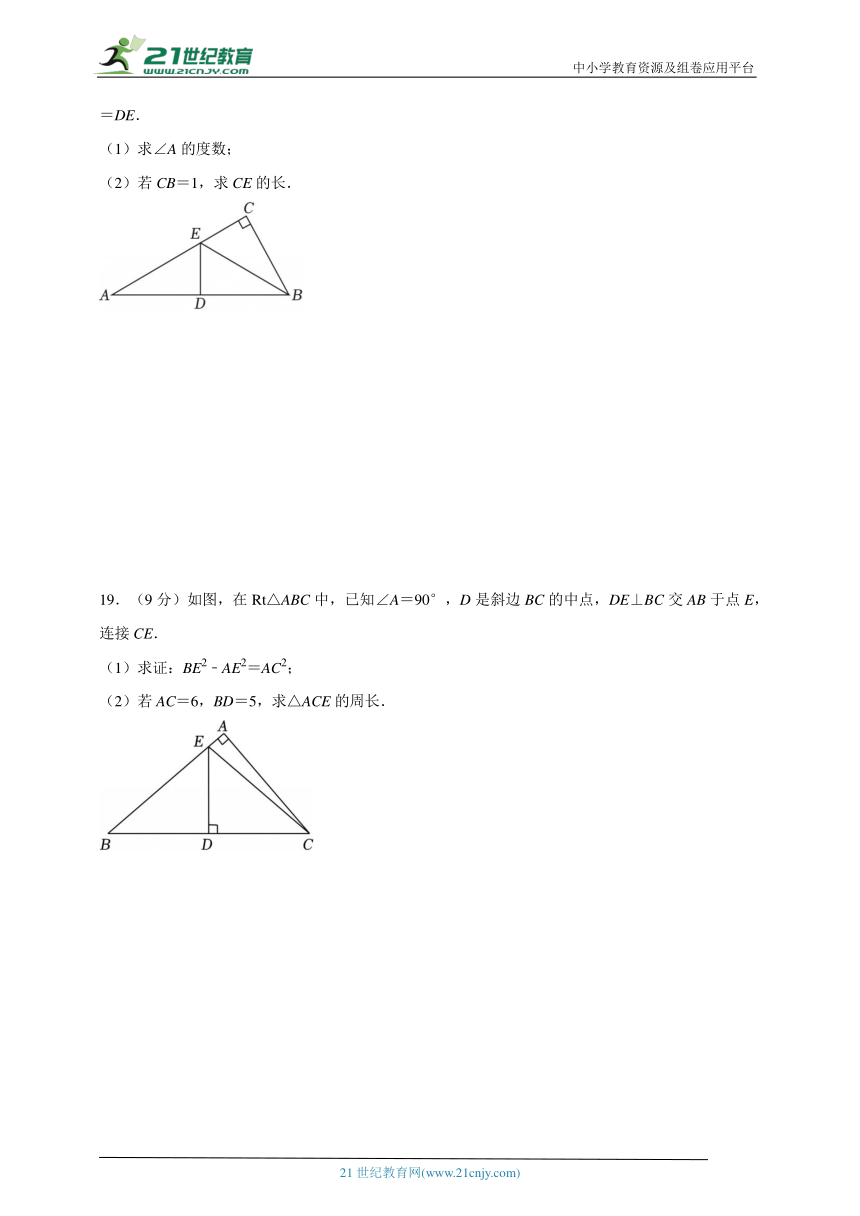
文档简介
中小学教育资源及组卷应用平台
第17章 勾股定理 培优提能测试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列各组数中,组成勾股数的是( )
A.0.6,0.8,1 B.,, C.8,15,17 D.4,5,6
2.在直角坐标系中,点P(3,﹣2)到原点的距离是( )
A. B. C. D.3
3.下列命题的逆命题成立的是( )
A.对顶角相等 B.全等三角形的对应角相等
C.等腰三角形两底角相等 D.如果两数相等,那么它们的绝对值相等
4.将一副直角三角板和一把宽度为1的直尺按如图方式摆放:先把60°和45°角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上,这两个三角板的斜边分别交直尺上沿于A,B两点,则线段AB的长是( )
A. B. C.1 D.
5.勾股定理与黄金分割并称为几何学中的两大瑰宝.勾股定理的发现可以称为是数学史上的里程碑,2000多年来,人们对它进行了大量的研究,至今已有几百种证法.利用图形中有关面积的等量关系可以证明勾股定理,利用如图①的直角三角形纸片拼成的②③④⑤四个图形中,可以证明勾股定理的图形有( )个.
A.1 B.2 C.3 D.4
6.如图,在由边长为1个单位长度的小正方形组成的网格中,线段AB的两个端点都在正方形网格的格点上,则AB的长度可能是( )
A. B. C. D.
7.如图,在水塔O的东北方向5m处有一抽水站A,在水塔的东南方12m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )
A.10m B.13m C.14m D.8m
8.△ABC三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a:b:c=5:12:13;③∠A:∠B:∠C=3:4:5;④a=32,b=42,c=52.其中能判断△ABC是直角三角形的个数有( )
A.1个 B.2个 C.3个 D.4个
9.雪上项目占据了2022年北京冬奥会的大部分比赛项目,有自由式滑雪、越野滑雪、跳台滑雪、无舵雪橇、有舵雪橇、高山滑雪等.如图,某滑雪运动员在坡度为5:12的雪道上下滑65m,则该滑雪运动员沿竖直方向下降的高度为( )
A.13m B.25m C.m D.156 m
10.如图,△OA1A2为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3,再以OA3为直角边作等腰直角三角形OA3A4,…,按此规律作下去,则OAn的长度为( )
A.()n B.()n﹣1 C.()n D.()n﹣1
(10题图) (11题图) (12题图) (13题图)
二.填空题(共15小题,满分15分,每小题3分)
11.如图,在正方形网格中,每个小正方形的边长都为1,点A、B、C在小正方形的格点上,连接AB,BC,则∠ABC= .
12.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a、b,斜边长为c,若b﹣a=4,c=20,则每个直角三角形的面积为 .
13.如图,网格中每个小正方形的边长都是1,点A,B,C,D都在小正方形的顶点上.则以AB,CD,为边的三角形的形状为 .
14.在△ABC中,AB=15,AC=13,BC边上的高AD=12,则边BC的长是 .
15.把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=2,则CD= .
三.解答题(共8小题,满分75分)
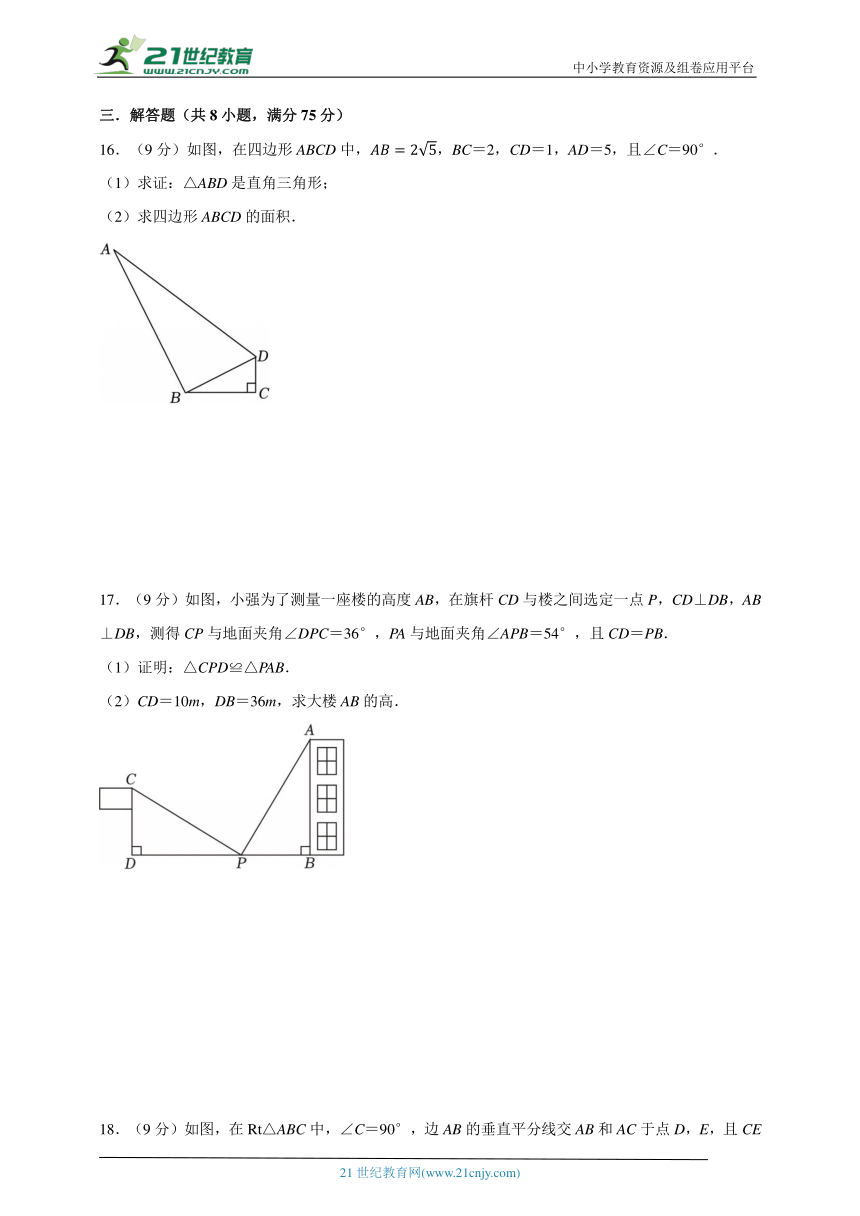
16.(9分)如图,在四边形ABCD中,,BC=2,CD=1,AD=5,且∠C=90°.
(1)求证:△ABD是直角三角形;
(2)求四边形ABCD的面积.
17.(9分)如图,小强为了测量一座楼的高度AB,在旗杆CD与楼之间选定一点P,CD⊥DB,AB⊥DB,测得CP与地面夹角∠DPC=36°,PA与地面夹角∠APB=54°,且CD=PB.
(1)证明:△CPD≌△PAB.
(2)CD=10m,DB=36m,求大楼AB的高.
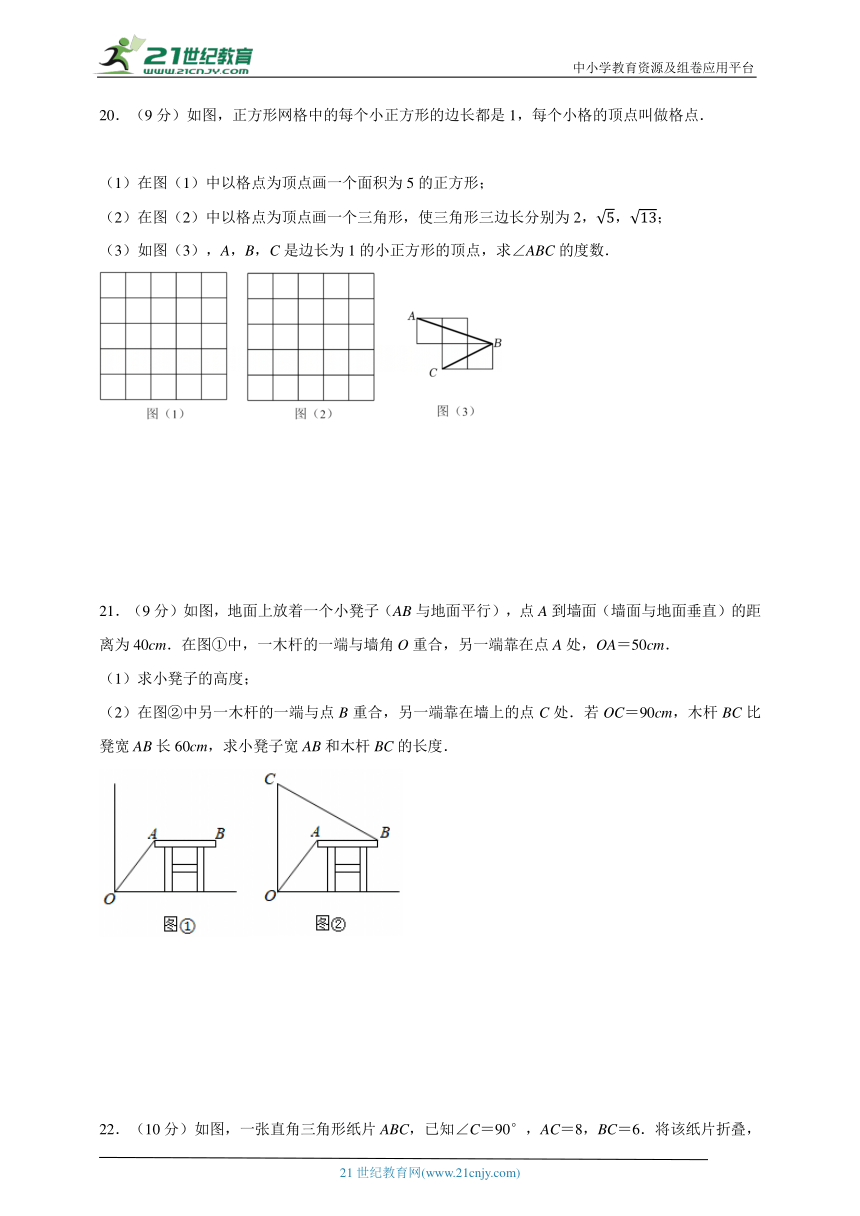
18.(9分)如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AB和AC于点D,E,且CE=DE.
(1)求∠A的度数;
(2)若CB=1,求CE的长.
19.(9分)如图,在Rt△ABC中,已知∠A=90°,D是斜边BC的中点,DE⊥BC交AB于点E,连接CE.
(1)求证:BE2﹣AE2=AC2;
(2)若AC=6,BD=5,求△ACE的周长.
20.(9分)如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图(1)中以格点为顶点画一个面积为5的正方形;
(2)在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为2,,;
(3)如图(3),A,B,C是边长为1的小正方形的顶点,求∠ABC的度数.
21.(9分)如图,地面上放着一个小凳子(AB与地面平行),点A到墙面(墙面与地面垂直)的距离为40cm.在图①中,一木杆的一端与墙角O重合,另一端靠在点A处,OA=50cm.
(1)求小凳子的高度;
(2)在图②中另一木杆的一端与点B重合,另一端靠在墙上的点C处.若OC=90cm,木杆BC比凳宽AB长60cm,求小凳子宽AB和木杆BC的长度.
22.(10分)如图,一张直角三角形纸片ABC,已知∠C=90°,AC=8,BC=6.将该纸片折叠,若折叠后点A与点B重合,折痕DE与边AC交于点D,与边AB交于点E.
(1)求△ABC的面积;
(2)求AB的长;
(3)求折痕DE的长.
23.(11分)在学习完勾股定理这一章后,小梦和小璐进行了如下对话.
小梦:如果一个三角形的三边长a,b,c满足a2+b2=2c2,那我们称这个三角形为“类勾股三角形”,例如△ABC的三边长分别是,和2,因为()2+()2=2×22,所以△ABC是“类勾股三角形”.
小璐:那等边三角形一定是“类勾股三角形”!
根据对话回答问题:
(1)判断:小璐的说法 ;(填“正确”或“错误”)
(2)已知△ABC的其中两边长分别为1,,若△ABC为“类勾股三角形”,则另一边长为 ;
(3)如果Rt△ABC是“类勾股三角形”,它的三边长分别为x,y,z(x,y为直角边长且x<y,z为斜边长),用只含有x的式子表示其周长和面积.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:由题意知,A、B中不是正整数,不能组成勾股数,故不符合要求;
C中82+152=289=172,能组成勾股数,故符合要求;
D中42+52=41≠36=62,不能组成勾股数,故不符合要求;
故选:C.
2.解:作PA⊥x轴于A,则PA=2,OA=3,
则根据勾股定理,得OP,
故选:B.
3.解:A、逆命题为:相等的角为对顶角,错误,不成立,不符合题意;
B、逆命题为:对应角相等的三角形全等,错误,不成立,不符合题意;
C、逆命题为:两角相等的三角形是等腰三角形,正确,成立,符合题意;
D、逆命题为:绝对值相等的两个数相等,错误,不成立,不符合题意;
故选:C.
4.解:在Rt△ACD中,∠ACD=45°,
∴∠CAD=45°=∠ACD,
∴AD=CD=1,
在Rt△BCD中,∠BCD=60°,
∴∠CBD=30°,
∴BC=2CD=2,
∴BD,
∴AB=BD﹣AD1.
故选:B.
5.解:在图②中,无法用面积的等量关系证明勾股定理;
在图③中,梯形的面积等于三个直角三角形的面积的和,
即(a+b)(a+b)ab×2c2,
化简得:a2+b2=c2;
在图④中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,
即c2ab×4+(b﹣a)2,
化简得:a2+b2=c2;
在图⑤中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,
即(a+b)2=c2ab×4,
化简得:a2+b2=c2;
故选:C.
6.解:当AB在正方形的边上时,AB的长为:1,2,3;
当AB在格点的对角线上时,如图,
AB或AB或AB或AB2或AB或AB3.
故选:B.
7.解:已知东北方向和东南方向刚好是一直角,
∴∠AOB=90°,
又∵OA=5m,OB=12m,
∴AB(m).
故选:B.
8.解:①∵∠A=∠B﹣∠C,∠A+∠B+∠C=180°,
∴∠B=90°,
故△ABC是直角三角形;
②a:b:c=5:12:13,可得:a2+b2=c2,
故△ABC是直角三角形;
③∠A:∠B:∠C=3:4:5,最大角∠C,
故△ABC不是直角三角形;
④a=32,b=42,c=52,
∴(32)2+(42)2≠(52)2,
故△ABC不是直角三角形;
∴是直角三角形的有2个;
故选:B.
9.解:如图,
由题意得,AB=65m,BC⊥AC于C,
∵斜坡AB的坡比是5:12,
∴设BC=5a,则AC=12a,
由勾股定理可得AB13a,
∴13a=65,
解得a=5,
∴BC=5a=25,
故选:B.
10.解:∵△OA1A2为等腰直角三角形,OA1=1,
∴OA2;
∵△OA2A3为等腰直角三角形,
∴OA3=2;
∵△OA3A4为等腰直角三角形,
∴OA4=2.
∵△OA4A5为等腰直角三角形,
∴OA5=4,
……
∴OAn的长度为()n﹣1.
故选:B.
二.填空题(共15小题,满分15分,每小题3分)
11.解:连接AC,
由勾股定理得:AB=AC,BC,
∴BC2=AC2+AB2,
∴△ABC是直角三角形,
∵AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
故答案为:45°.
12.解:由图可得,
a2+b2=c2,
∴且a、b均大于0,
解得,
∴每个直角三角形的面积为ab12×16=96,
故答案为:96.
13.解:由图可得,AB2=42+22=20,CD2=22+22=8,
∵EF2=(2)2=12,
∴CD2+EF2=12+8=20=AB2,
∴以AB、CD、EF三条线段为边的三角形的形状为直角三角形.
故答案为:直角三角形.
14.解:如图1,在△ABC中,AB=15,AC=13,BC边上的高AD=12,
∴BD9,
CD5,
∴BC=BD+DC=14;
如图2,在Rt△ABD中,AB=15,AD=12,
∴BD9,
在Rt△ACD中,由勾股定理得,
CD5,
∴BC=BD﹣CD=9﹣5=4,
综上所述,BC的长为14或4,
故答案为:14或4.
15.解:如图,过点A作AF⊥BC于F,
在Rt△ABC中,∠B=45°,
∴BCAB=2,BF=AFAB2,
∵两个同样大小的含45°角的三角尺,
∴AD=BC=2,
在Rt△ADF中,根据勾股定理得,DF,
∴CD=BF+DF﹣BC2,
故答案为:.
三.解答题(共8小题,满分75分)
16.(1)证明:在Rt△BCD中,
∵∠C=90°,BC=2,CD=1,
由勾股定理得,BC2+CD2=BD2,
∴.
在△ABD中,,,AD=5.
∵,
∴AB2+BD2=AD2.
由勾股逆定理可得,∠ABD=90°,
∴△ABD是直角三角形;
(2)解:S四边形ABCD=S△ABD+S△BCD.
17.(1)证明:由条件可知∠DCP=∠APB=54°,
在△CPD和△PAB中,
∵∠CDP=∠ABP,DC=PB,∠DCP=∠APB,
∴△CPD≌△PAB(ASA);
(2)解:∵△CPD≌△PAB,
∴DP=AB.
∵DB=36米,PB=10米,
∴AB=36﹣10=26(米).
答:楼AB高是26米.
18.解:(1)∵∠C=90°,DE⊥AB,CE=DE,
∴BE平分∠ABC,
∴∠CBE=∠ABE,
∵DE的垂直平分AB,
∴EA=EB,
∴∠ABE=∠A.
∴∠CBE=∠ABE=∠A,
∵∠C=90°,
∴∠CBE+∠ABE+∠A=90°,
即3∠A=90°,
∴∠A=30°;
(2)∵∠CBE=∠ABE=∠A=30°,∠C=90°,
∴BE=2CE,
在Rt△BCE中,根据勾股定理得CE2+BC2=BE2,
∵BC=1,
∴CE2+12=(2CE)2,
解得CE.
19.(1)证明:∵D是斜边BC的中点,DE⊥BC,
∴DE是线段BC的垂直平分线,
∴BE=CE.
在Rt△ACE中,由勾股定理得CE2=AC2+AE2,
∴BE2=AC2+AE2,
即BE2﹣AE2=AC2.
(2)解:∵D是斜边BC的中点,BD=5,
∴BC=2BD=10.
在Rt△ABC中,由勾股定理得,
∴AB=BE+AE=8.
又∵BE=CE,
∴CE+AE=8,
∴△ACE的周长为CE+AE+AC=8+6=14.
20.解:(1)所画正方形如图(1)所示,
(2)所画三角形如图(2)所示,
(3)连接AC,如图(3),
由勾股定理,得AC=BC,AB,
∵AC2+BC2=5+5=10,AB2=10,
∴AC2+BC2=AB2,
∴△ABC为等腰直角三角形,且∠ACB=90°,
∴∠ABC=45°.
21.解:(1)过A作AM垂直于墙面,垂足M,
根据题意可得,AM=40cm,
在Rt△AOM中,OM30,
即凳子的高度为30cm.
(2)延长BA交墙面于点N,可得∠BNC=90°,
设AB=x cm,则CB=x+60,BN=x+40,CN=90﹣30=60,
在Rt△BCN中,BN2+CN2=BC2,即(40+x)2+602=(60+x)2,
解得x=40,则BC=60+40=100(cm).
22.解:(1)∵△ABC是直角三角形,AC=8,BC=6,
∴S△ABCAC BC8×6=24;
(2)∵△ABC是直角三角形,AC=8,BC=6,
∴AB10;(4分)
(3)连接BD,设CD=x,
∵△ADE≌△BDE,
∴AE=BE=5,AD=BD,
设CD=x,则AD=BD=8﹣x,在Rt△BCD中,
BD2=CD2+BC2,即(8﹣x)2=x2+36,(5分)
解得,DC,AD=BD=8,(6分)
同理,在Rt△BDE中,
DE.(7分)
23.解:(1)设等边三角形三边长分别是a,b,c,则a=b=c,
∴a2+b2=2c2,
∴等边三角形是“类勾股三角形”,
∴小璐的说法正确.
故答案为:正确;
(2)设另一边长为x,
①12+()2=2x2,解得x=2,符合题意;
②12+x2=2()2,解得x,符合题意;
③x2+()2=2×12,x无解;
故答案为:2或;
(3)∵Rt△ABC是“类勾股三角形”且x<y,z为斜边长,
∴x2+z2=2y2,
由勾股定理得x2+y2=z2,
整理得x2+x2+y2=2y2,即2x2=y2,
∴yx,
∴z2=3x2,
∴zx,
∴Rt△ABC的周长为x+y+z=(1)x,
Rt△ABC的面积为xyx xx2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第17章 勾股定理 培优提能测试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列各组数中,组成勾股数的是( )
A.0.6,0.8,1 B.,, C.8,15,17 D.4,5,6
2.在直角坐标系中,点P(3,﹣2)到原点的距离是( )
A. B. C. D.3
3.下列命题的逆命题成立的是( )
A.对顶角相等 B.全等三角形的对应角相等
C.等腰三角形两底角相等 D.如果两数相等,那么它们的绝对值相等
4.将一副直角三角板和一把宽度为1的直尺按如图方式摆放:先把60°和45°角的顶点及它们的直角边重合,再将此直角边垂直于直尺的上沿,重合的顶点落在直尺下沿上,这两个三角板的斜边分别交直尺上沿于A,B两点,则线段AB的长是( )
A. B. C.1 D.
5.勾股定理与黄金分割并称为几何学中的两大瑰宝.勾股定理的发现可以称为是数学史上的里程碑,2000多年来,人们对它进行了大量的研究,至今已有几百种证法.利用图形中有关面积的等量关系可以证明勾股定理,利用如图①的直角三角形纸片拼成的②③④⑤四个图形中,可以证明勾股定理的图形有( )个.
A.1 B.2 C.3 D.4
6.如图,在由边长为1个单位长度的小正方形组成的网格中,线段AB的两个端点都在正方形网格的格点上,则AB的长度可能是( )
A. B. C. D.
7.如图,在水塔O的东北方向5m处有一抽水站A,在水塔的东南方12m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )
A.10m B.13m C.14m D.8m
8.△ABC三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a:b:c=5:12:13;③∠A:∠B:∠C=3:4:5;④a=32,b=42,c=52.其中能判断△ABC是直角三角形的个数有( )
A.1个 B.2个 C.3个 D.4个
9.雪上项目占据了2022年北京冬奥会的大部分比赛项目,有自由式滑雪、越野滑雪、跳台滑雪、无舵雪橇、有舵雪橇、高山滑雪等.如图,某滑雪运动员在坡度为5:12的雪道上下滑65m,则该滑雪运动员沿竖直方向下降的高度为( )
A.13m B.25m C.m D.156 m
10.如图,△OA1A2为等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3,再以OA3为直角边作等腰直角三角形OA3A4,…,按此规律作下去,则OAn的长度为( )
A.()n B.()n﹣1 C.()n D.()n﹣1
(10题图) (11题图) (12题图) (13题图)
二.填空题(共15小题,满分15分,每小题3分)
11.如图,在正方形网格中,每个小正方形的边长都为1,点A、B、C在小正方形的格点上,连接AB,BC,则∠ABC= .
12.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a、b,斜边长为c,若b﹣a=4,c=20,则每个直角三角形的面积为 .
13.如图,网格中每个小正方形的边长都是1,点A,B,C,D都在小正方形的顶点上.则以AB,CD,为边的三角形的形状为 .
14.在△ABC中,AB=15,AC=13,BC边上的高AD=12,则边BC的长是 .
15.把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=2,则CD= .
三.解答题(共8小题,满分75分)
16.(9分)如图,在四边形ABCD中,,BC=2,CD=1,AD=5,且∠C=90°.
(1)求证:△ABD是直角三角形;
(2)求四边形ABCD的面积.
17.(9分)如图,小强为了测量一座楼的高度AB,在旗杆CD与楼之间选定一点P,CD⊥DB,AB⊥DB,测得CP与地面夹角∠DPC=36°,PA与地面夹角∠APB=54°,且CD=PB.
(1)证明:△CPD≌△PAB.
(2)CD=10m,DB=36m,求大楼AB的高.
18.(9分)如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线交AB和AC于点D,E,且CE=DE.
(1)求∠A的度数;
(2)若CB=1,求CE的长.
19.(9分)如图,在Rt△ABC中,已知∠A=90°,D是斜边BC的中点,DE⊥BC交AB于点E,连接CE.
(1)求证:BE2﹣AE2=AC2;
(2)若AC=6,BD=5,求△ACE的周长.
20.(9分)如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图(1)中以格点为顶点画一个面积为5的正方形;
(2)在图(2)中以格点为顶点画一个三角形,使三角形三边长分别为2,,;
(3)如图(3),A,B,C是边长为1的小正方形的顶点,求∠ABC的度数.
21.(9分)如图,地面上放着一个小凳子(AB与地面平行),点A到墙面(墙面与地面垂直)的距离为40cm.在图①中,一木杆的一端与墙角O重合,另一端靠在点A处,OA=50cm.
(1)求小凳子的高度;
(2)在图②中另一木杆的一端与点B重合,另一端靠在墙上的点C处.若OC=90cm,木杆BC比凳宽AB长60cm,求小凳子宽AB和木杆BC的长度.
22.(10分)如图,一张直角三角形纸片ABC,已知∠C=90°,AC=8,BC=6.将该纸片折叠,若折叠后点A与点B重合,折痕DE与边AC交于点D,与边AB交于点E.
(1)求△ABC的面积;
(2)求AB的长;
(3)求折痕DE的长.
23.(11分)在学习完勾股定理这一章后,小梦和小璐进行了如下对话.
小梦:如果一个三角形的三边长a,b,c满足a2+b2=2c2,那我们称这个三角形为“类勾股三角形”,例如△ABC的三边长分别是,和2,因为()2+()2=2×22,所以△ABC是“类勾股三角形”.
小璐:那等边三角形一定是“类勾股三角形”!
根据对话回答问题:
(1)判断:小璐的说法 ;(填“正确”或“错误”)
(2)已知△ABC的其中两边长分别为1,,若△ABC为“类勾股三角形”,则另一边长为 ;
(3)如果Rt△ABC是“类勾股三角形”,它的三边长分别为x,y,z(x,y为直角边长且x<y,z为斜边长),用只含有x的式子表示其周长和面积.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:由题意知,A、B中不是正整数,不能组成勾股数,故不符合要求;
C中82+152=289=172,能组成勾股数,故符合要求;
D中42+52=41≠36=62,不能组成勾股数,故不符合要求;
故选:C.
2.解:作PA⊥x轴于A,则PA=2,OA=3,
则根据勾股定理,得OP,
故选:B.
3.解:A、逆命题为:相等的角为对顶角,错误,不成立,不符合题意;
B、逆命题为:对应角相等的三角形全等,错误,不成立,不符合题意;
C、逆命题为:两角相等的三角形是等腰三角形,正确,成立,符合题意;
D、逆命题为:绝对值相等的两个数相等,错误,不成立,不符合题意;
故选:C.
4.解:在Rt△ACD中,∠ACD=45°,
∴∠CAD=45°=∠ACD,
∴AD=CD=1,
在Rt△BCD中,∠BCD=60°,
∴∠CBD=30°,
∴BC=2CD=2,
∴BD,
∴AB=BD﹣AD1.
故选:B.
5.解:在图②中,无法用面积的等量关系证明勾股定理;
在图③中,梯形的面积等于三个直角三角形的面积的和,
即(a+b)(a+b)ab×2c2,
化简得:a2+b2=c2;
在图④中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,
即c2ab×4+(b﹣a)2,
化简得:a2+b2=c2;
在图⑤中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,
即(a+b)2=c2ab×4,
化简得:a2+b2=c2;
故选:C.
6.解:当AB在正方形的边上时,AB的长为:1,2,3;
当AB在格点的对角线上时,如图,
AB或AB或AB或AB2或AB或AB3.
故选:B.
7.解:已知东北方向和东南方向刚好是一直角,
∴∠AOB=90°,
又∵OA=5m,OB=12m,
∴AB(m).
故选:B.
8.解:①∵∠A=∠B﹣∠C,∠A+∠B+∠C=180°,
∴∠B=90°,
故△ABC是直角三角形;
②a:b:c=5:12:13,可得:a2+b2=c2,
故△ABC是直角三角形;
③∠A:∠B:∠C=3:4:5,最大角∠C,
故△ABC不是直角三角形;
④a=32,b=42,c=52,
∴(32)2+(42)2≠(52)2,
故△ABC不是直角三角形;
∴是直角三角形的有2个;
故选:B.
9.解:如图,
由题意得,AB=65m,BC⊥AC于C,
∵斜坡AB的坡比是5:12,
∴设BC=5a,则AC=12a,
由勾股定理可得AB13a,
∴13a=65,
解得a=5,
∴BC=5a=25,
故选:B.
10.解:∵△OA1A2为等腰直角三角形,OA1=1,
∴OA2;
∵△OA2A3为等腰直角三角形,
∴OA3=2;
∵△OA3A4为等腰直角三角形,
∴OA4=2.
∵△OA4A5为等腰直角三角形,
∴OA5=4,
……
∴OAn的长度为()n﹣1.
故选:B.
二.填空题(共15小题,满分15分,每小题3分)
11.解:连接AC,
由勾股定理得:AB=AC,BC,
∴BC2=AC2+AB2,
∴△ABC是直角三角形,
∵AB=AC,
∴△ABC是等腰直角三角形,
∴∠ABC=45°,
故答案为:45°.
12.解:由图可得,
a2+b2=c2,
∴且a、b均大于0,
解得,
∴每个直角三角形的面积为ab12×16=96,
故答案为:96.
13.解:由图可得,AB2=42+22=20,CD2=22+22=8,
∵EF2=(2)2=12,
∴CD2+EF2=12+8=20=AB2,
∴以AB、CD、EF三条线段为边的三角形的形状为直角三角形.
故答案为:直角三角形.
14.解:如图1,在△ABC中,AB=15,AC=13,BC边上的高AD=12,
∴BD9,
CD5,
∴BC=BD+DC=14;
如图2,在Rt△ABD中,AB=15,AD=12,
∴BD9,
在Rt△ACD中,由勾股定理得,
CD5,
∴BC=BD﹣CD=9﹣5=4,
综上所述,BC的长为14或4,
故答案为:14或4.
15.解:如图,过点A作AF⊥BC于F,
在Rt△ABC中,∠B=45°,
∴BCAB=2,BF=AFAB2,
∵两个同样大小的含45°角的三角尺,
∴AD=BC=2,
在Rt△ADF中,根据勾股定理得,DF,
∴CD=BF+DF﹣BC2,
故答案为:.
三.解答题(共8小题,满分75分)
16.(1)证明:在Rt△BCD中,
∵∠C=90°,BC=2,CD=1,
由勾股定理得,BC2+CD2=BD2,
∴.
在△ABD中,,,AD=5.
∵,
∴AB2+BD2=AD2.
由勾股逆定理可得,∠ABD=90°,
∴△ABD是直角三角形;
(2)解:S四边形ABCD=S△ABD+S△BCD.
17.(1)证明:由条件可知∠DCP=∠APB=54°,
在△CPD和△PAB中,
∵∠CDP=∠ABP,DC=PB,∠DCP=∠APB,
∴△CPD≌△PAB(ASA);
(2)解:∵△CPD≌△PAB,
∴DP=AB.
∵DB=36米,PB=10米,
∴AB=36﹣10=26(米).
答:楼AB高是26米.
18.解:(1)∵∠C=90°,DE⊥AB,CE=DE,
∴BE平分∠ABC,
∴∠CBE=∠ABE,
∵DE的垂直平分AB,
∴EA=EB,
∴∠ABE=∠A.
∴∠CBE=∠ABE=∠A,
∵∠C=90°,
∴∠CBE+∠ABE+∠A=90°,
即3∠A=90°,
∴∠A=30°;
(2)∵∠CBE=∠ABE=∠A=30°,∠C=90°,
∴BE=2CE,
在Rt△BCE中,根据勾股定理得CE2+BC2=BE2,
∵BC=1,
∴CE2+12=(2CE)2,
解得CE.
19.(1)证明:∵D是斜边BC的中点,DE⊥BC,
∴DE是线段BC的垂直平分线,
∴BE=CE.
在Rt△ACE中,由勾股定理得CE2=AC2+AE2,
∴BE2=AC2+AE2,
即BE2﹣AE2=AC2.
(2)解:∵D是斜边BC的中点,BD=5,
∴BC=2BD=10.
在Rt△ABC中,由勾股定理得,
∴AB=BE+AE=8.
又∵BE=CE,
∴CE+AE=8,
∴△ACE的周长为CE+AE+AC=8+6=14.
20.解:(1)所画正方形如图(1)所示,
(2)所画三角形如图(2)所示,
(3)连接AC,如图(3),
由勾股定理,得AC=BC,AB,
∵AC2+BC2=5+5=10,AB2=10,
∴AC2+BC2=AB2,
∴△ABC为等腰直角三角形,且∠ACB=90°,
∴∠ABC=45°.
21.解:(1)过A作AM垂直于墙面,垂足M,
根据题意可得,AM=40cm,
在Rt△AOM中,OM30,
即凳子的高度为30cm.
(2)延长BA交墙面于点N,可得∠BNC=90°,
设AB=x cm,则CB=x+60,BN=x+40,CN=90﹣30=60,
在Rt△BCN中,BN2+CN2=BC2,即(40+x)2+602=(60+x)2,
解得x=40,则BC=60+40=100(cm).
22.解:(1)∵△ABC是直角三角形,AC=8,BC=6,
∴S△ABCAC BC8×6=24;
(2)∵△ABC是直角三角形,AC=8,BC=6,
∴AB10;(4分)
(3)连接BD,设CD=x,
∵△ADE≌△BDE,
∴AE=BE=5,AD=BD,
设CD=x,则AD=BD=8﹣x,在Rt△BCD中,
BD2=CD2+BC2,即(8﹣x)2=x2+36,(5分)
解得,DC,AD=BD=8,(6分)
同理,在Rt△BDE中,
DE.(7分)
23.解:(1)设等边三角形三边长分别是a,b,c,则a=b=c,
∴a2+b2=2c2,
∴等边三角形是“类勾股三角形”,
∴小璐的说法正确.
故答案为:正确;
(2)设另一边长为x,
①12+()2=2x2,解得x=2,符合题意;
②12+x2=2()2,解得x,符合题意;
③x2+()2=2×12,x无解;
故答案为:2或;
(3)∵Rt△ABC是“类勾股三角形”且x<y,z为斜边长,
∴x2+z2=2y2,
由勾股定理得x2+y2=z2,
整理得x2+x2+y2=2y2,即2x2=y2,
∴yx,
∴z2=3x2,
∴zx,
∴Rt△ABC的周长为x+y+z=(1)x,
Rt△ABC的面积为xyx xx2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
