人教版五年级上册6 多边形的面积梯形的面积(课件)(共16张PPT)
文档属性
| 名称 | 人教版五年级上册6 多边形的面积梯形的面积(课件)(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-20 19:45:14 | ||
图片预览




文档简介
(共16张PPT)
梯形的面积
回顾反思
自主练习
合作探索
情境导入
[教学目标]
1.在自主探索、合作交流中经历梯形面积公式的推导过程,掌握梯形面积的计算方法,并能灵活运用公式解决相关的数学问题。
2.通过猜想、验证、实践等数学活动,发展空间观念和推理能力,获得解决问题的多种策略,感受数学方法的内在魅力。
3.通过探索活动,激发学习兴趣、培养严谨、科学的学习态度、勇于探索、乐于合作的精神。
[教学重点]梯形面积公式的应用。
[教学难点]梯形面积公式的推导过程。
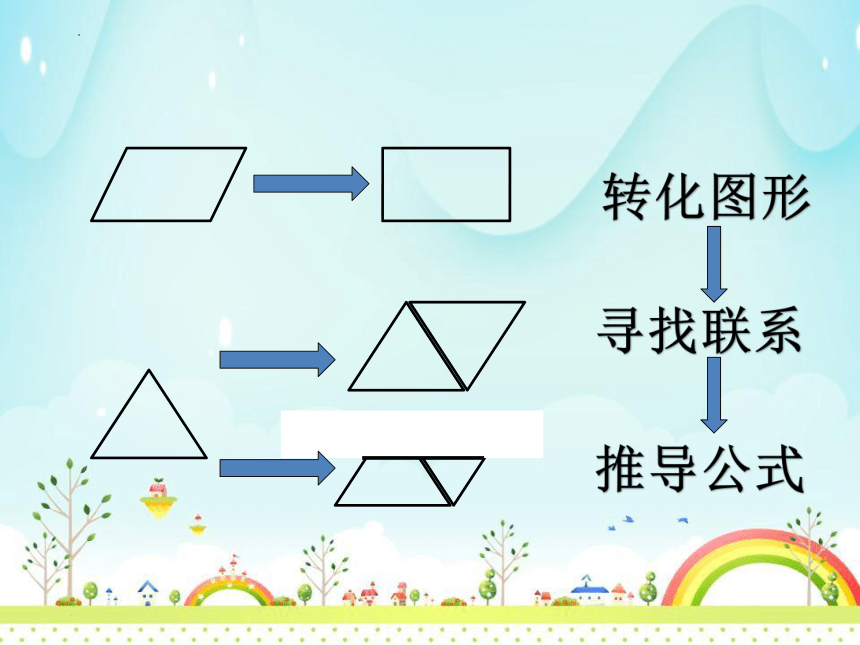
转化图形
寻找联系
推导公式
一、情境导入
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
上底:32厘米
下底:36厘米
高: 32厘米
制作这个椅子面需要多少平方厘米的木材?
1.想办法研究出手中的梯形有多少个面积单位?
2.说说你是怎么得到这个结果的?
3.研究出梯形的面积公式是什么?
活动要求
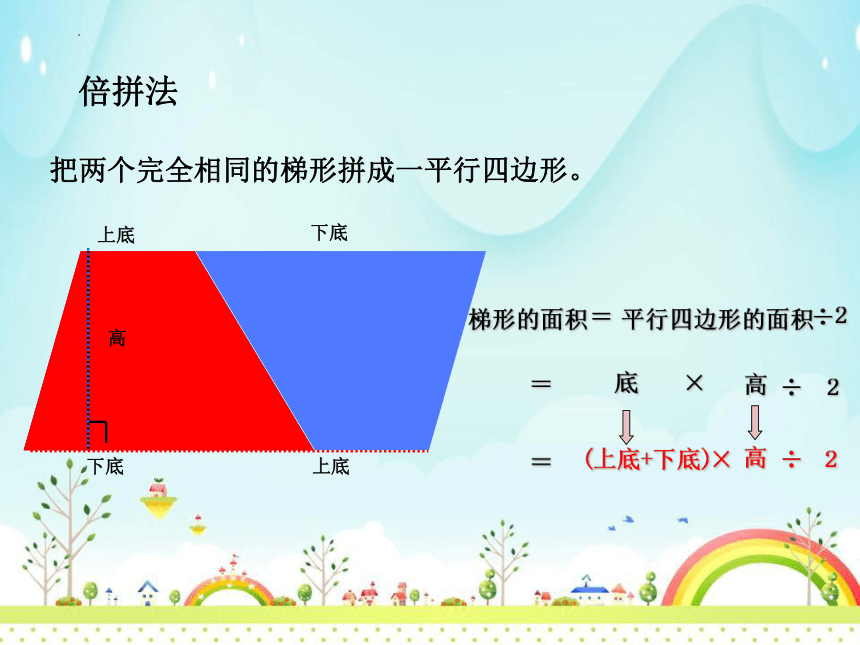
把两个完全相同的梯形拼成一平行四边形。
梯形的面积
÷
2
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
=
下底
上底
高
下底
上底
倍拼法
高÷2
上底+下底
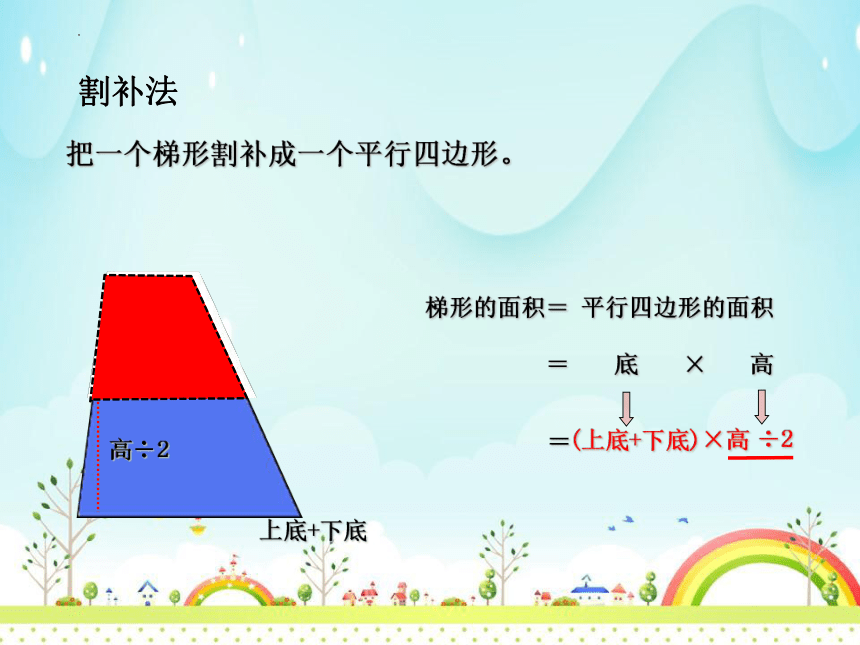
梯形的面积= 平行四边形的面积
=
底
×
高
(上底+下底)
÷2
×高
=
把一个梯形割补成一个平行四边形。
割补法
高
上底
下底
上底×高÷2
分割法
把一个梯形分割成两个三角形。
(上底+下底)
下底×高 ÷2
+
÷2
×高
=
梯形的面积
两个三角形的面积之和
=
=
高
上底
下底
上底
把一个梯形割补成一个大三角形。
高
分割法
梯形的面积
=
×
高
÷
2
用字母表示:
S
(上底+下底)
=
(a+b)
h
÷
2
高不变、底不变,面积变成了原来的两倍。
底不变、面积不变,高变成了原来的一半。
(32+36)×32÷2
制作这个椅子面需要多少平方厘米的木材?
=68×32÷2
=2176÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
计算下面图形的面积。
智勇大闯关:第一关
(18+9)×10÷2
=27×10÷2
=135(dm2)
9dm
18dm
10dm
12dm
14dm
450×2÷(15+35)
=450×2÷50
=18(米)
答:花坛的高是18米
一个梯形的花坛,上底为15米,下底为35米,面积是450平方米,那么花坛的高是多少米?
35米
15米
450平方米
=900÷50
智勇大闯关:第二关
转化的数学思想
知识
方法
情感
应用
合作
梯形的面积
回顾反思
自主练习
合作探索
情境导入
[教学目标]
1.在自主探索、合作交流中经历梯形面积公式的推导过程,掌握梯形面积的计算方法,并能灵活运用公式解决相关的数学问题。
2.通过猜想、验证、实践等数学活动,发展空间观念和推理能力,获得解决问题的多种策略,感受数学方法的内在魅力。
3.通过探索活动,激发学习兴趣、培养严谨、科学的学习态度、勇于探索、乐于合作的精神。
[教学重点]梯形面积公式的应用。
[教学难点]梯形面积公式的推导过程。
转化图形
寻找联系
推导公式
一、情境导入
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
上底:32厘米
下底:36厘米
高: 32厘米
制作这个椅子面需要多少平方厘米的木材?
1.想办法研究出手中的梯形有多少个面积单位?
2.说说你是怎么得到这个结果的?
3.研究出梯形的面积公式是什么?
活动要求
把两个完全相同的梯形拼成一平行四边形。
梯形的面积
÷
2
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
=
下底
上底
高
下底
上底
倍拼法
高÷2
上底+下底
梯形的面积= 平行四边形的面积
=
底
×
高
(上底+下底)
÷2
×高
=
把一个梯形割补成一个平行四边形。
割补法
高
上底
下底
上底×高÷2
分割法
把一个梯形分割成两个三角形。
(上底+下底)
下底×高 ÷2
+
÷2
×高
=
梯形的面积
两个三角形的面积之和
=
=
高
上底
下底
上底
把一个梯形割补成一个大三角形。
高
分割法
梯形的面积
=
×
高
÷
2
用字母表示:
S
(上底+下底)
=
(a+b)
h
÷
2
高不变、底不变,面积变成了原来的两倍。
底不变、面积不变,高变成了原来的一半。
(32+36)×32÷2
制作这个椅子面需要多少平方厘米的木材?
=68×32÷2
=2176÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
计算下面图形的面积。
智勇大闯关:第一关
(18+9)×10÷2
=27×10÷2
=135(dm2)
9dm
18dm
10dm
12dm
14dm
450×2÷(15+35)
=450×2÷50
=18(米)
答:花坛的高是18米
一个梯形的花坛,上底为15米,下底为35米,面积是450平方米,那么花坛的高是多少米?
35米
15米
450平方米
=900÷50
智勇大闯关:第二关
转化的数学思想
知识
方法
情感
应用
合作
