第18章 平行四边形 培优测试题(含答案)
文档属性
| 名称 | 第18章 平行四边形 培优测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 04:47:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第18章 平行四边形 培优测试题
考试范围:第18章 平行四边形;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.如图,在 ABCD中,若∠A=30°,则∠B的度数为( )
A.30° B.60° C.90° D.150°
2.如图, ABCD的对角线AC、BD相交于点O,如果添加一个条件使得 ABCD是矩形,那么下列添加的条件中正确的是( )
A.∠DAO+∠ADO=90° B.∠DAC=∠ACD
C.∠DAC=∠BAC D.∠DAB=∠ABC
3.如图,公路AC,BC互相垂直,点M为公路AB的中点,为测量湖泊两侧C、M两点间的距离,若测得AB的长为5m,则M,C两点间的距离为( )
A.2.5cm B.3cm C.4.5cm D.5cm
(1题图) (2题图) (3题图) (5题图)
4.在平行四边形ABCD中,∠A+∠C=160°,则∠D等于( )
A.50° B.80° C.100° D.130°
5.如图,在 ABCD中,AC,BD交于点O,AE平分∠BAD交BC于点E,连接OE,2AB=BC=AC=4,则△OCE的面积为( )
A. B. C. D.
6.如图,两张等宽的纸条交叉叠放在一起,重合部分构成四边形ABCD,且对角线AC=8,BD=6,则纸条的宽度是( )
A.9.6 B.5 C.4.8 D.2.4
7.如图,在菱形ABCD中,∠B=60°,AB=6,E,F分别是边CD和BC的延长线上一点,且CE=CF=2,以CE,CF为边作 CEGF,H是AG的中点.则线段CH的长为( )
A. B. C. D.
8.如图,在平行四边形ABCD中,AD=6,BD=8,AD⊥DB,点M、N分别是边AB、BC上的动点(不与A、B、C重合),点E、F分别为DN、MN的中点,连接EF,则EF的最小值为( )
A.2.4 B.3 C.4 D.4.8
9.如图,矩形ABCD中,AB=12,BC=5,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( )
A. B.7 C.8 D.
10.如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论:
①OGAB;②与△DEG、全等的三角形共有5个;③四边形ODEG与四边形OBAG面积相等;④由点A、B、D、E构成的四边形是菱形.其中一定成立的是( )
A.①③④ B.①②③ C.①②④ D.②③④
(8题图) (9题图) (10题图)
二.填空题(共5小题,满分15分,每小题3分)
11.如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,连接EF.只需添加一个条件即可证明四边形EFCB是菱形,这个条件可以是 (写出一个即可).
12.如图,在 ABCD中,∠A=68°,DB=DC,CE⊥BD于E,则∠BCE的度数为 .
(11题图) (12题图) (13题图) (14题图)
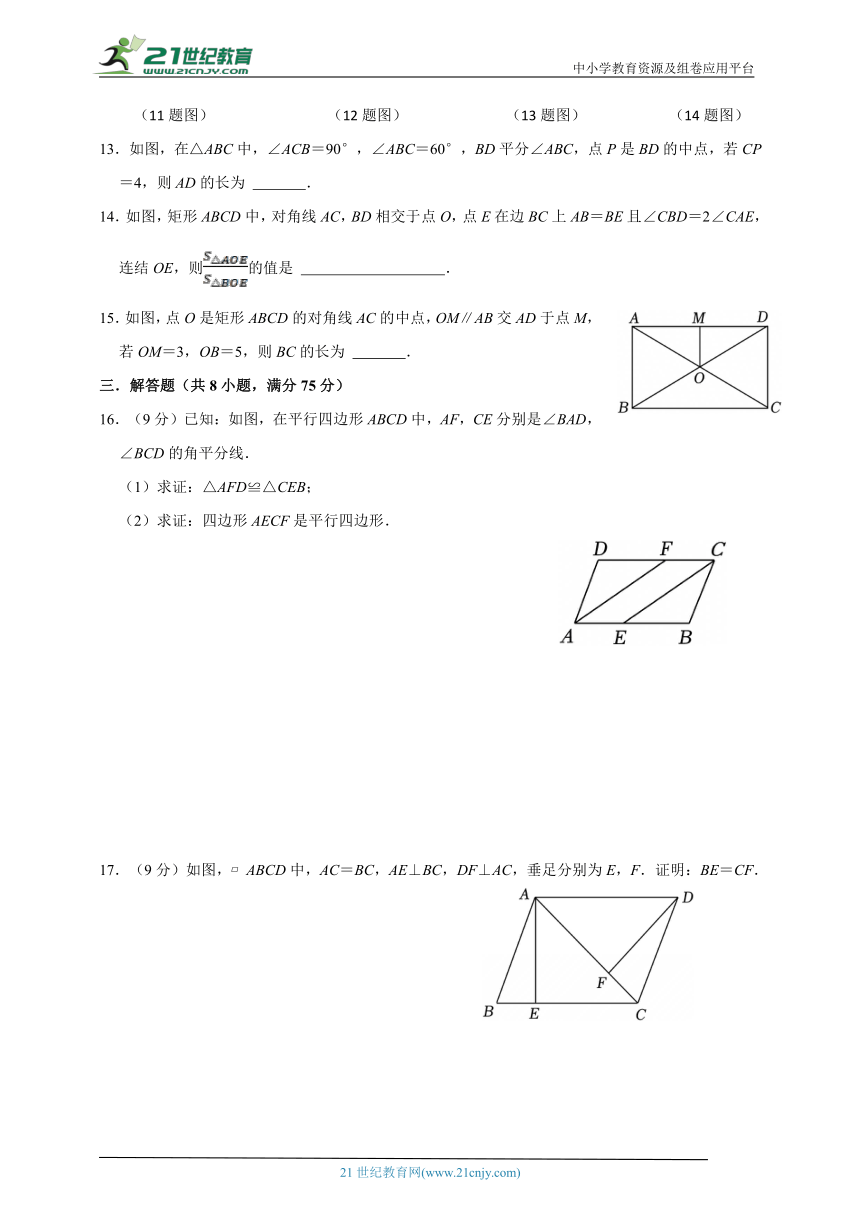
13.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,点P是BD的中点,若CP=4,则AD的长为 .
14.如图,矩形ABCD中,对角线AC,BD相交于点O,点E在边BC上AB=BE且∠CBD=2∠CAE,连结OE,则的值是 .
15.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,OB=5,则BC的长为 .
三.解答题(共8小题,满分75分)
16.(9分)已知:如图,在平行四边形ABCD中,AF,CE分别是∠BAD,∠BCD的角平分线.
(1)求证:△AFD≌△CEB;
(2)求证:四边形AECF是平行四边形.
17.(9分)如图, ABCD中,AC=BC,AE⊥BC,DF⊥AC,垂足分别为E,F.证明:BE=CF.
18.(9分)课本再现
(1)如图1,O是正方形ABCD对角线的交点,同时,O是正方形A1B1C1O的一个顶点,且这两个正方形的边长相等,两个正方形重叠的部分为四边形EBFO,则S四边形EBFO= S正方形ABCD;AE BF(填“>”“=”或“<”).
拓展延伸
(2)如图2,正方形ABCD的对角线AC,BD相交于点O,E是边AD上一点,连接OE,过点O作OF⊥OE,交CD于点F.若四边形OFDE的面积是1,求线段AB的长.
19.(9分)如图,平行四边形ABCD中,P是AB边上的一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ.
(1)若CQ平分∠DCP,求证:四边形ABCD是矩形;
(2)在(1)的条件下,当AP=2,CB=4时,求CD的长.
20.(9分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,EF⊥AB于F点,OG∥EF交AB于点G.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BD的长.
21.(9分)如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=13,AC=24,求四边形AECD的面积.
22.(10分)如图,在矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F.
(1)证明:四边形EBFD是菱形;
(2)若BF=2,∠EBF=60°,求BD的长.
23.(11分)在正方形ABCD中,E是BC边上一点(点E不与点B,C重合),AE⊥EF,垂足为点E,EF与正方形的外角∠DCG的平分线交于点F.
(1)如图1,若点E是BC的中点,猜想AE与EF的数量关系是 ;证明此猜想时,可取AB的中点P,连接EP.根据此图形易证△AEP≌△EFC.则判断△AEP≌△EFC的依据是 .
(2)点E在BC边上运动.
①如图2,(1)中的猜想是否仍然成立?请说明理由.
②如图3,连接AF,DF,若正方形ABCD的边长为1,直接写出△AFD的周长c的取值范围.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵四边形ABCD是平行四边形,∠A=30°,
∴AD∥BC,
∴∠B+∠A=180°,
∴∠B=180°﹣30°=150°.
选:D.
2.解:A、∵∠DAO+∠ADO=90°,
∴∠AOD=90°,
∴AC⊥BD,
∴ ABCD是菱形,选项A不符合题意;
B、∵∠DAC=∠ACD,
∴AD=CD,
∴ ABCD是菱形,选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DCA=∠BAC,
∵∠DAC=∠BAC,
∴∠DCA=∠DAC,
∴AD=CD,
∴ ABCD是菱形,选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠DAB+∠ABC=180°,
∵∠DAB=∠ABC,
∴∠DAB=∠ABC=90°,
∴ ABCD是矩形,选项D符合题意;
选:D.
3.解:∵公路AC,BC互相垂直,
∴∠ACB=90°,
∵M为AB的中点,
∴CMAB,
∵AB=5m,
∴CM=2.5(m),
即M,C两点间的距离为2.5m,
选:A.
4.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠A+∠D=180°,
∵∠A+∠C=160°,
∴∠A=80°,
∴∠D=180°﹣∠A=100°.
选:C.
5.解:∵ ABCD,AE平分∠BAD,AD∥BC,
∴∠DAE=∠BEA,∠DAE=∠BAE,
∴∠BEA=∠BAE,
∴,即E为BC的中点,
∴;
如图,作CF⊥AB于F,
∵AC=BC,
∴,
由勾股定理得,,
∴,
∴,
选:B.
6.解:过点D作DH⊥AB于点H,过点D作DF⊥BC于F,设AC、BD交点为O.
∵两条纸条宽度相同,
∴DH=DF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵S ABCD=AB DH=BC DF,
又∵DH=DF.
∴BC=AB,
∴四边形ABCD是菱形;
∴OB=ODBD=3,OA=OCAC=4,AC⊥BD.
∴AB5,
∴AB DHAC BD,
∴DH,
∴纸条的宽度是是4.8;
选:C.
7.解:如图,连接AC,CG,EF,CG与EF交于点O.
∵四边形ABCD是菱形,
∴AB∥CD,BA=BC,
∴∠B=∠ECF=60°,△ABC是等边三角形,
∴AC=AB=6,∠ACB=∠ACD=60°,
∵四边形CEGF是平行四边形,
∵CE=CF=2,
∴四边形CEGF是菱形,
∴EF⊥CG,∠ECG=∠GCF=30°,
∴OE=OFCE=1,
∴OC=OG,
∴∠ACG=90°,CG=2,
∴AG4,
∵AH=HG,
∴CHAG=2.
选:D.
8.解:∵AD=6,BD=8,AD⊥DB,
∴AB10,
如图,连接DM,
∵E、F分别为DN、MN的中点,
∴EF是△DMN的中位线,
∴EFDM,
∴EF的最小值,就是DM的最小值,
当DM⊥AB时,DM最小,
∵S△ADBAD BDAB DM,
∴DM,
∴EFDM=2.4,
∴EF的最小值为2.4.
选:A.
9.解:连接EF交AC于点O,如图所示,
∵四边形ABCD是矩形,
∴∠ABC=90°,DC∥AB,
∴∠FCO=∠EAO,
∵AB=12,BC=5,
∴AC13,
∵四边形EGFH是菱形,
∴EF⊥GH,OF=OE,
∴∠AOE=∠COF=90°,
∴△COF≌△AOE(AAS),
∴OC=OA,
∵∠AOE=90°,∠ABC=90°,
∴∠AOE=∠ABC,
又∵∠OAE=∠BAC,
∴△AOE∽△ABC,
∴,
即,
解得AE,
选:D.
10.解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD(SSS),
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OGCDAB,①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,④正确;
∴AD⊥BE,
由菱形的性质得:△BGA≌△BGD≌△EGD(SSS),
在△BGA和△COD中,
,
∴△BGA≌△COD(SAS),
∴△AOB≌△COB≌△COD≌△AOD≌△BGA≌△BGD≌△EGD,②不正确;
∵OB=OD,
∴S△BOG=S△DOG,
∵四边形ABDE是菱形,
∴S△ABG=S△DGE,
∴四边形ODEG与四边形OBAG面积相等,③正确;
选:A.
二.填空题(共5小题,满分15分,每小题3分)
11.解:这个条件可以是CF=CB,理由如下:,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵E,F分别是AB,CD的中点,
∴BEAB,CFCD,
∴BE=CF,
∴四边形EFCB是平行四边形,
又∵CF=CB,
∴平行四边形EFCB是菱形,
答案为:CF=CB(答案不唯一).
12.解:∵四边形ABCD是平行四边形,
∴∠BCD=∠A=68°,
∵DB=DC,
∴∠DBC=∠BCD=68°,
∵CE⊥BD,
∴∠CEB=90°,
∴∠BCE=90°﹣68°=22°.
答案为:22°.
13.解:在Rt△BCD中,点P是BD的中点,
∴CP是中线,
∴BD=2CP=8,
∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC.
∴∠DBA=∠A=30°,
∴BD=AD=8,
答案为:8.
14.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=OCAC,OB=ODBD,AC=BD,AD∥BC,
∴OB=OC,
∴∠OCB=∠OBC,
∵AD∥BC,
∴∠DAO=∠OCB,
∴∠DAO=∠OBC,
∵∠CBD=2∠CAE,
∴∠DAO=2∠CAE,
∵AB=BE,∠ABC=90°,
∴△ABE是等腰直角三角形,
∴∠BAE=45°,
∴∠DAE=90°﹣45°=45°,
∴∠DAO=2∠CAE,
∴∠DAO=30°,
∴∠ACB=30°,
∴BCABBE,
∴EC=BC﹣BE=(1)BE,
∴1,
∵OA=OC,
∴△AOE的面积=△COE的面积,
∴1.
答案为:1.
15.解:∵点O是矩形ABCD的对角线AC的中点,
∴OA=OB=OD=OC=5,∠BAD=90°,BC=AD,
∵OM∥AB,
∴∠OMA=180°﹣∠BAD=90°,
∴AD=2AM,
∵OM=3,
∴,
∴BC=AD=2AM=8;
答案为:8.
三.解答题(共8小题,满分75分)
16.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠BAD=∠BCD,AB∥CD,
∵AF,CE分别为∠BAD和∠BCD的角平分线,
∴∠BAF=∠DAF=∠BCE=∠DCE,
在△DAF和△BCE中,
,
∴△AFD≌△CEB(ASA);
(2)∵△AFD≌△CEB,
∴DF=BE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形.
17.证明:∵AE⊥BC,DF⊥AC,
∴∠AEB=∠DFC=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAC=∠ACD,
∵AC=BC,
∴∠B=∠BAC,
∴∠B=∠ACD,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(AAS),
∴BE=CF.
18.解:(1)如图,连接OA=OB,
∵O是正方形ABCD对角线的交点,
∴OA=OB∠OAE=∠OBF=45°,∠AOB=90°;
∴∠AOE+∠EOB=90°;
在正方形A1B1C1O中,∠A1OC1=∠EOB+∠BOF=90°,
∴∠AOE=∠BOF,
∴△OAE≌△OBF(ASA),
∴S△OAE=S△OBF,AE=BF,
∴S△AOB=S△AOE+S△EOB=S△OBF+S△EOB=S四边形EBFO,
∵,AB2=OA2+OB2=2OA2,S正方形ABCD=AB2,
∴,
∴,
∴,
答案为:;=;
(2)∵O是正方形ABCD对角线的交点,
∴OD=OC,∠ODE=∠OCF=45°,∠DOC=90°,
∴∠DOF+∠FOC=90°;
∵OF⊥OE,∠EOD+∠DOF=90°,
∴∠EOD=∠FOC,
∴△ODE≌△OCF(ASA),
∴S△ODE=S△OCF,
∴S△COD=S△DOF+S△FOC=S△DOF+S△DOE=S四边形EDFO=1,
∴.
∴OD2=2,
∵CD2=OD2+OC2=2OD2=4,
∴AB=CD=2.
19.(1)证明:∵PQ⊥CP,
∴∠CPQ=90°,
∵CQ平分∠DCP,
∴∠DCQ=∠PCQ,
又∵CP=CD,CQ=CQ,
∴△DCQ≌△PCQ(SAS),
∴∠D=∠QPC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵CP=CD,
∴设CP=CD=x,则PB=x﹣2,
在Rt△BCP中,BC2+BP2=CP2,
∴(x﹣2)2+42=x2,
∴x=5,
∴CD=5.
20.(1)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=10,AC⊥BD,
∴∠AOD=90°,
∵E是AD的中点,
∴,
由(1)可知,四边形EFCO是矩形,
∴FG=OE=5,
∵EF⊥AB,
∴∠EFA=90°,
∴,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2,
∵在直角三角形OGB中OB2=BG2+OG2=22+42=20,
∴,
∴.
21.(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OE=OD,
∵AO=CO,
∴四边形AECD是平行四边形.
(2)解:∵AB=BC,AO=CO,
∴BO⊥AC,
∴四边形AECD是菱形.
在Rt△COD中,CD=13,OCAC=12,
∴OD5,
∴DE=2OD=10,
∴菱形AECD的面积AC DE24×10=120.
22.(1)证明:∵四边形ABCD是矩形,O是对角线BD的中点,
∴AD∥BC,OB=OD,
∴∠FBO=∠EDO,又∠BOF=∠DOE,
在△BOF和△DOE中,
,
∴△BOF≌△DOE(ASA),
∴BF=DE,又DE∥BF,
∴四边形EBFD是平行四边形,
∵EF⊥BD,
∴四边形EBFD是菱形;
(2)解:∵四边形EBFD是菱形,
∴∠FBO∠EBF=30°,
∵∠BOF=90°,
∴OFBF=1,
∴OB,
∴BD=2OB=2.
23.解:(1)如图1,取AB的中点P,连接EP.
则AP=BPAB,
∵点E是BC的中点,
∴BE=CEBC,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=90°,
∴AP=EC,∠BAE+∠AEB=90°,BP=BE,∠DCG=90°,
∴△BPE是等腰直角三角形,
∴∠BPE=45°,
∴∠APE=180°﹣∠BPE=180°﹣45°=135°,
∵CF平分∠DCG,
∴∠DCF=∠GCF=45°,
∴∠ECF=180°﹣∠GCF=180°﹣45°=135°,
∴∠APE=∠ECF,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠CEF,
在△AEP和△EFC中,
,
∴△AEP≌△EFC(ASA),
∴AE=EF,
答案为:AE=EF,ASA;
(2)①成立,理由如下:
如图2,在AB上取一点P,使BP=BE,连接PE,
则AP=EC,
由(1)得:∠PAE=∠CEF,
∵BP=BE,∠B=90°,
∴△BPE是等腰直角三角形,
∴∠BPE=45°,
∴∠APE=180°﹣∠BPE=180°﹣45°=135°,
∴∠APE=∠ECF,
在△AEP和△EFC中,
,
∴△AEP≌△EFC(ASA),
∴AE=EF;
②如图3,过D作DH⊥CF交DG于点H,连接FH、AH,
∵∠DCF=45°,
∴∠CDH=45°,
∴△DCH是等腰直角三角形,
∴点H与D关于CF对称,
∴DF=HF,
∴AF+DF=AF+FH,
当A、F、H三点共线时,AF+FH即AF+DF最短,
此时AF+DF=AH,BH=BC+CH=2,
在Rt△ABH中,由勾股定理得:AH,
此时c=AD+AF+DF=1;
当DF=FH与CD相等时,即A、D、F三点共线,
此时AD+AF+DF=1+2+1=4,
则c<AD+AF+DF=4;
∴△AFD的周长c的取值范围是1c<4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第18章 平行四边形 培优测试题
考试范围:第18章 平行四边形;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.如图,在 ABCD中,若∠A=30°,则∠B的度数为( )
A.30° B.60° C.90° D.150°
2.如图, ABCD的对角线AC、BD相交于点O,如果添加一个条件使得 ABCD是矩形,那么下列添加的条件中正确的是( )
A.∠DAO+∠ADO=90° B.∠DAC=∠ACD
C.∠DAC=∠BAC D.∠DAB=∠ABC
3.如图,公路AC,BC互相垂直,点M为公路AB的中点,为测量湖泊两侧C、M两点间的距离,若测得AB的长为5m,则M,C两点间的距离为( )
A.2.5cm B.3cm C.4.5cm D.5cm
(1题图) (2题图) (3题图) (5题图)
4.在平行四边形ABCD中,∠A+∠C=160°,则∠D等于( )
A.50° B.80° C.100° D.130°
5.如图,在 ABCD中,AC,BD交于点O,AE平分∠BAD交BC于点E,连接OE,2AB=BC=AC=4,则△OCE的面积为( )
A. B. C. D.
6.如图,两张等宽的纸条交叉叠放在一起,重合部分构成四边形ABCD,且对角线AC=8,BD=6,则纸条的宽度是( )
A.9.6 B.5 C.4.8 D.2.4
7.如图,在菱形ABCD中,∠B=60°,AB=6,E,F分别是边CD和BC的延长线上一点,且CE=CF=2,以CE,CF为边作 CEGF,H是AG的中点.则线段CH的长为( )
A. B. C. D.
8.如图,在平行四边形ABCD中,AD=6,BD=8,AD⊥DB,点M、N分别是边AB、BC上的动点(不与A、B、C重合),点E、F分别为DN、MN的中点,连接EF,则EF的最小值为( )
A.2.4 B.3 C.4 D.4.8
9.如图,矩形ABCD中,AB=12,BC=5,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( )
A. B.7 C.8 D.
10.如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论:
①OGAB;②与△DEG、全等的三角形共有5个;③四边形ODEG与四边形OBAG面积相等;④由点A、B、D、E构成的四边形是菱形.其中一定成立的是( )
A.①③④ B.①②③ C.①②④ D.②③④
(8题图) (9题图) (10题图)
二.填空题(共5小题,满分15分,每小题3分)
11.如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,连接EF.只需添加一个条件即可证明四边形EFCB是菱形,这个条件可以是 (写出一个即可).
12.如图,在 ABCD中,∠A=68°,DB=DC,CE⊥BD于E,则∠BCE的度数为 .
(11题图) (12题图) (13题图) (14题图)
13.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,点P是BD的中点,若CP=4,则AD的长为 .
14.如图,矩形ABCD中,对角线AC,BD相交于点O,点E在边BC上AB=BE且∠CBD=2∠CAE,连结OE,则的值是 .
15.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,OB=5,则BC的长为 .
三.解答题(共8小题,满分75分)
16.(9分)已知:如图,在平行四边形ABCD中,AF,CE分别是∠BAD,∠BCD的角平分线.
(1)求证:△AFD≌△CEB;
(2)求证:四边形AECF是平行四边形.
17.(9分)如图, ABCD中,AC=BC,AE⊥BC,DF⊥AC,垂足分别为E,F.证明:BE=CF.
18.(9分)课本再现
(1)如图1,O是正方形ABCD对角线的交点,同时,O是正方形A1B1C1O的一个顶点,且这两个正方形的边长相等,两个正方形重叠的部分为四边形EBFO,则S四边形EBFO= S正方形ABCD;AE BF(填“>”“=”或“<”).
拓展延伸
(2)如图2,正方形ABCD的对角线AC,BD相交于点O,E是边AD上一点,连接OE,过点O作OF⊥OE,交CD于点F.若四边形OFDE的面积是1,求线段AB的长.
19.(9分)如图,平行四边形ABCD中,P是AB边上的一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ.
(1)若CQ平分∠DCP,求证:四边形ABCD是矩形;
(2)在(1)的条件下,当AP=2,CB=4时,求CD的长.
20.(9分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,EF⊥AB于F点,OG∥EF交AB于点G.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BD的长.
21.(9分)如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,满足∠EAO=∠DCO.
(1)求证:四边形AECD是平行四边形;
(2)若AB=BC,CD=13,AC=24,求四边形AECD的面积.
22.(10分)如图,在矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F.
(1)证明:四边形EBFD是菱形;
(2)若BF=2,∠EBF=60°,求BD的长.
23.(11分)在正方形ABCD中,E是BC边上一点(点E不与点B,C重合),AE⊥EF,垂足为点E,EF与正方形的外角∠DCG的平分线交于点F.
(1)如图1,若点E是BC的中点,猜想AE与EF的数量关系是 ;证明此猜想时,可取AB的中点P,连接EP.根据此图形易证△AEP≌△EFC.则判断△AEP≌△EFC的依据是 .
(2)点E在BC边上运动.
①如图2,(1)中的猜想是否仍然成立?请说明理由.
②如图3,连接AF,DF,若正方形ABCD的边长为1,直接写出△AFD的周长c的取值范围.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵四边形ABCD是平行四边形,∠A=30°,
∴AD∥BC,
∴∠B+∠A=180°,
∴∠B=180°﹣30°=150°.
选:D.
2.解:A、∵∠DAO+∠ADO=90°,
∴∠AOD=90°,
∴AC⊥BD,
∴ ABCD是菱形,选项A不符合题意;
B、∵∠DAC=∠ACD,
∴AD=CD,
∴ ABCD是菱形,选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠DCA=∠BAC,
∵∠DAC=∠BAC,
∴∠DCA=∠DAC,
∴AD=CD,
∴ ABCD是菱形,选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠DAB+∠ABC=180°,
∵∠DAB=∠ABC,
∴∠DAB=∠ABC=90°,
∴ ABCD是矩形,选项D符合题意;
选:D.
3.解:∵公路AC,BC互相垂直,
∴∠ACB=90°,
∵M为AB的中点,
∴CMAB,
∵AB=5m,
∴CM=2.5(m),
即M,C两点间的距离为2.5m,
选:A.
4.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AB∥CD,
∴∠A+∠D=180°,
∵∠A+∠C=160°,
∴∠A=80°,
∴∠D=180°﹣∠A=100°.
选:C.
5.解:∵ ABCD,AE平分∠BAD,AD∥BC,
∴∠DAE=∠BEA,∠DAE=∠BAE,
∴∠BEA=∠BAE,
∴,即E为BC的中点,
∴;
如图,作CF⊥AB于F,
∵AC=BC,
∴,
由勾股定理得,,
∴,
∴,
选:B.
6.解:过点D作DH⊥AB于点H,过点D作DF⊥BC于F,设AC、BD交点为O.
∵两条纸条宽度相同,
∴DH=DF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵S ABCD=AB DH=BC DF,
又∵DH=DF.
∴BC=AB,
∴四边形ABCD是菱形;
∴OB=ODBD=3,OA=OCAC=4,AC⊥BD.
∴AB5,
∴AB DHAC BD,
∴DH,
∴纸条的宽度是是4.8;
选:C.
7.解:如图,连接AC,CG,EF,CG与EF交于点O.
∵四边形ABCD是菱形,
∴AB∥CD,BA=BC,
∴∠B=∠ECF=60°,△ABC是等边三角形,
∴AC=AB=6,∠ACB=∠ACD=60°,
∵四边形CEGF是平行四边形,
∵CE=CF=2,
∴四边形CEGF是菱形,
∴EF⊥CG,∠ECG=∠GCF=30°,
∴OE=OFCE=1,
∴OC=OG,
∴∠ACG=90°,CG=2,
∴AG4,
∵AH=HG,
∴CHAG=2.
选:D.
8.解:∵AD=6,BD=8,AD⊥DB,
∴AB10,
如图,连接DM,
∵E、F分别为DN、MN的中点,
∴EF是△DMN的中位线,
∴EFDM,
∴EF的最小值,就是DM的最小值,
当DM⊥AB时,DM最小,
∵S△ADBAD BDAB DM,
∴DM,
∴EFDM=2.4,
∴EF的最小值为2.4.
选:A.
9.解:连接EF交AC于点O,如图所示,
∵四边形ABCD是矩形,
∴∠ABC=90°,DC∥AB,
∴∠FCO=∠EAO,
∵AB=12,BC=5,
∴AC13,
∵四边形EGFH是菱形,
∴EF⊥GH,OF=OE,
∴∠AOE=∠COF=90°,
∴△COF≌△AOE(AAS),
∴OC=OA,
∵∠AOE=90°,∠ABC=90°,
∴∠AOE=∠ABC,
又∵∠OAE=∠BAC,
∴△AOE∽△ABC,
∴,
即,
解得AE,
选:D.
10.解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD(SSS),
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位线,
∴OGCDAB,①正确;
∵AB∥CE,AB=DE,
∴四边形ABDE是平行四边形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等边三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四边形ABDE是菱形,④正确;
∴AD⊥BE,
由菱形的性质得:△BGA≌△BGD≌△EGD(SSS),
在△BGA和△COD中,
,
∴△BGA≌△COD(SAS),
∴△AOB≌△COB≌△COD≌△AOD≌△BGA≌△BGD≌△EGD,②不正确;
∵OB=OD,
∴S△BOG=S△DOG,
∵四边形ABDE是菱形,
∴S△ABG=S△DGE,
∴四边形ODEG与四边形OBAG面积相等,③正确;
选:A.
二.填空题(共5小题,满分15分,每小题3分)
11.解:这个条件可以是CF=CB,理由如下:,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵E,F分别是AB,CD的中点,
∴BEAB,CFCD,
∴BE=CF,
∴四边形EFCB是平行四边形,
又∵CF=CB,
∴平行四边形EFCB是菱形,
答案为:CF=CB(答案不唯一).
12.解:∵四边形ABCD是平行四边形,
∴∠BCD=∠A=68°,
∵DB=DC,
∴∠DBC=∠BCD=68°,
∵CE⊥BD,
∴∠CEB=90°,
∴∠BCE=90°﹣68°=22°.
答案为:22°.
13.解:在Rt△BCD中,点P是BD的中点,
∴CP是中线,
∴BD=2CP=8,
∵∠ACB=90°,∠ABC=60°,
∴∠A=30°,
∵BD平分∠ABC.
∴∠DBA=∠A=30°,
∴BD=AD=8,
答案为:8.
14.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=OCAC,OB=ODBD,AC=BD,AD∥BC,
∴OB=OC,
∴∠OCB=∠OBC,
∵AD∥BC,
∴∠DAO=∠OCB,
∴∠DAO=∠OBC,
∵∠CBD=2∠CAE,
∴∠DAO=2∠CAE,
∵AB=BE,∠ABC=90°,
∴△ABE是等腰直角三角形,
∴∠BAE=45°,
∴∠DAE=90°﹣45°=45°,
∴∠DAO=2∠CAE,
∴∠DAO=30°,
∴∠ACB=30°,
∴BCABBE,
∴EC=BC﹣BE=(1)BE,
∴1,
∵OA=OC,
∴△AOE的面积=△COE的面积,
∴1.
答案为:1.
15.解:∵点O是矩形ABCD的对角线AC的中点,
∴OA=OB=OD=OC=5,∠BAD=90°,BC=AD,
∵OM∥AB,
∴∠OMA=180°﹣∠BAD=90°,
∴AD=2AM,
∵OM=3,
∴,
∴BC=AD=2AM=8;
答案为:8.
三.解答题(共8小题,满分75分)
16.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠D=∠B,∠BAD=∠BCD,AB∥CD,
∵AF,CE分别为∠BAD和∠BCD的角平分线,
∴∠BAF=∠DAF=∠BCE=∠DCE,
在△DAF和△BCE中,
,
∴△AFD≌△CEB(ASA);
(2)∵△AFD≌△CEB,
∴DF=BE,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形.
17.证明:∵AE⊥BC,DF⊥AC,
∴∠AEB=∠DFC=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAC=∠ACD,
∵AC=BC,
∴∠B=∠BAC,
∴∠B=∠ACD,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(AAS),
∴BE=CF.
18.解:(1)如图,连接OA=OB,
∵O是正方形ABCD对角线的交点,
∴OA=OB∠OAE=∠OBF=45°,∠AOB=90°;
∴∠AOE+∠EOB=90°;
在正方形A1B1C1O中,∠A1OC1=∠EOB+∠BOF=90°,
∴∠AOE=∠BOF,
∴△OAE≌△OBF(ASA),
∴S△OAE=S△OBF,AE=BF,
∴S△AOB=S△AOE+S△EOB=S△OBF+S△EOB=S四边形EBFO,
∵,AB2=OA2+OB2=2OA2,S正方形ABCD=AB2,
∴,
∴,
∴,
答案为:;=;
(2)∵O是正方形ABCD对角线的交点,
∴OD=OC,∠ODE=∠OCF=45°,∠DOC=90°,
∴∠DOF+∠FOC=90°;
∵OF⊥OE,∠EOD+∠DOF=90°,
∴∠EOD=∠FOC,
∴△ODE≌△OCF(ASA),
∴S△ODE=S△OCF,
∴S△COD=S△DOF+S△FOC=S△DOF+S△DOE=S四边形EDFO=1,
∴.
∴OD2=2,
∵CD2=OD2+OC2=2OD2=4,
∴AB=CD=2.
19.(1)证明:∵PQ⊥CP,
∴∠CPQ=90°,
∵CQ平分∠DCP,
∴∠DCQ=∠PCQ,
又∵CP=CD,CQ=CQ,
∴△DCQ≌△PCQ(SAS),
∴∠D=∠QPC=90°,
∴平行四边形ABCD是矩形;
(2)解:∵CP=CD,
∴设CP=CD=x,则PB=x﹣2,
在Rt△BCP中,BC2+BP2=CP2,
∴(x﹣2)2+42=x2,
∴x=5,
∴CD=5.
20.(1)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=10,AC⊥BD,
∴∠AOD=90°,
∵E是AD的中点,
∴,
由(1)可知,四边形EFCO是矩形,
∴FG=OE=5,
∵EF⊥AB,
∴∠EFA=90°,
∴,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2,
∵在直角三角形OGB中OB2=BG2+OG2=22+42=20,
∴,
∴.
21.(1)证明:在△AOE和△COD中,
,
∴△AOE≌△COD(ASA),
∴OE=OD,
∵AO=CO,
∴四边形AECD是平行四边形.
(2)解:∵AB=BC,AO=CO,
∴BO⊥AC,
∴四边形AECD是菱形.
在Rt△COD中,CD=13,OCAC=12,
∴OD5,
∴DE=2OD=10,
∴菱形AECD的面积AC DE24×10=120.
22.(1)证明:∵四边形ABCD是矩形,O是对角线BD的中点,
∴AD∥BC,OB=OD,
∴∠FBO=∠EDO,又∠BOF=∠DOE,
在△BOF和△DOE中,
,
∴△BOF≌△DOE(ASA),
∴BF=DE,又DE∥BF,
∴四边形EBFD是平行四边形,
∵EF⊥BD,
∴四边形EBFD是菱形;
(2)解:∵四边形EBFD是菱形,
∴∠FBO∠EBF=30°,
∵∠BOF=90°,
∴OFBF=1,
∴OB,
∴BD=2OB=2.
23.解:(1)如图1,取AB的中点P,连接EP.
则AP=BPAB,
∵点E是BC的中点,
∴BE=CEBC,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=90°,
∴AP=EC,∠BAE+∠AEB=90°,BP=BE,∠DCG=90°,
∴△BPE是等腰直角三角形,
∴∠BPE=45°,
∴∠APE=180°﹣∠BPE=180°﹣45°=135°,
∵CF平分∠DCG,
∴∠DCF=∠GCF=45°,
∴∠ECF=180°﹣∠GCF=180°﹣45°=135°,
∴∠APE=∠ECF,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AEB+∠FEC=90°,
∴∠BAE=∠CEF,
在△AEP和△EFC中,
,
∴△AEP≌△EFC(ASA),
∴AE=EF,
答案为:AE=EF,ASA;
(2)①成立,理由如下:
如图2,在AB上取一点P,使BP=BE,连接PE,
则AP=EC,
由(1)得:∠PAE=∠CEF,
∵BP=BE,∠B=90°,
∴△BPE是等腰直角三角形,
∴∠BPE=45°,
∴∠APE=180°﹣∠BPE=180°﹣45°=135°,
∴∠APE=∠ECF,
在△AEP和△EFC中,
,
∴△AEP≌△EFC(ASA),
∴AE=EF;
②如图3,过D作DH⊥CF交DG于点H,连接FH、AH,
∵∠DCF=45°,
∴∠CDH=45°,
∴△DCH是等腰直角三角形,
∴点H与D关于CF对称,
∴DF=HF,
∴AF+DF=AF+FH,
当A、F、H三点共线时,AF+FH即AF+DF最短,
此时AF+DF=AH,BH=BC+CH=2,
在Rt△ABH中,由勾股定理得:AH,
此时c=AD+AF+DF=1;
当DF=FH与CD相等时,即A、D、F三点共线,
此时AD+AF+DF=1+2+1=4,
则c<AD+AF+DF=4;
∴△AFD的周长c的取值范围是1c<4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
