人教版数学七年级下册期中复习题一【精华】(含答案)
文档属性
| 名称 | 人教版数学七年级下册期中复习题一【精华】(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 672.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 04:53:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学七年级下册期中复习题一【精华】
一、单选题
1.(2024八上·杭州月考)下列选项中,可以用来证明命题“若,则”的逆命题是假命题的反例是( )
A. B. C. D.
2.(2022八上·长春期末)下列命题中的假命题是( )
A.若,则
B.有一个角为的等腰三角形是等边三角形
C.若一个三角形有两个角相等,则这个三角形是等腰三角形
D.等腰三角形底边上的高平分它的顶角
3.(2024八上·深圳期中)下列运算正确的是( )
A. B. C. D.
4.(2024七下·南乐期末)如图,是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , ,则的度数为( )
A. B. C. D.
5.(2024八上·薛城期中)如图是雷达探测到的6个目标,若目标B用表示,目标F用表示,则表示为的目标是( )
A.目标A B.目标C C.目标D D.目标E
二、判断题
6.(2024七下·北京市月考)直线外一点到这条直线的垂线段叫做点到直线的距离
7.(2024七下·北京市月考)判断题:若,,则
8.判断下列语句哪些是命题,哪些不是命题(填“正确”或“错误”).
(1)方程2x-4=0的解是x=2.( )
(2)这朵小花是红色的.( )
(3)在△ABC中,若AB>AC,则∠C>∠B吗 ( )
(4)若ab>0,则a>0.( )
(5)两个相等的同位角的角平分线平行.( )
(6)两个无理数的和必是无理数.( )
(7)请画出一对对顶角.( )
(8)(a为实数).( )
判断题.
9.是5 的一个平方根;
10.的算术平方根是3;
11.的平方根是±2;
12.0的平方根与算术平方根都是0.
三、填空题
13.(2023八下·东昌府期末)的平方根为 .
14.(2024七上·广州期末)如图,是直线上一点,已知,,则 .
15.(2023七下·大竹期末)如图,,垂足为,过作.若,则 .
16.(2023八上·肃州期中)已知,则点关于x轴对称的点的坐标为 .
17.(2022·绵阳模拟)如图,,点E、F分别在直线、上,且,平分,交直线于点M,则的度数是 .
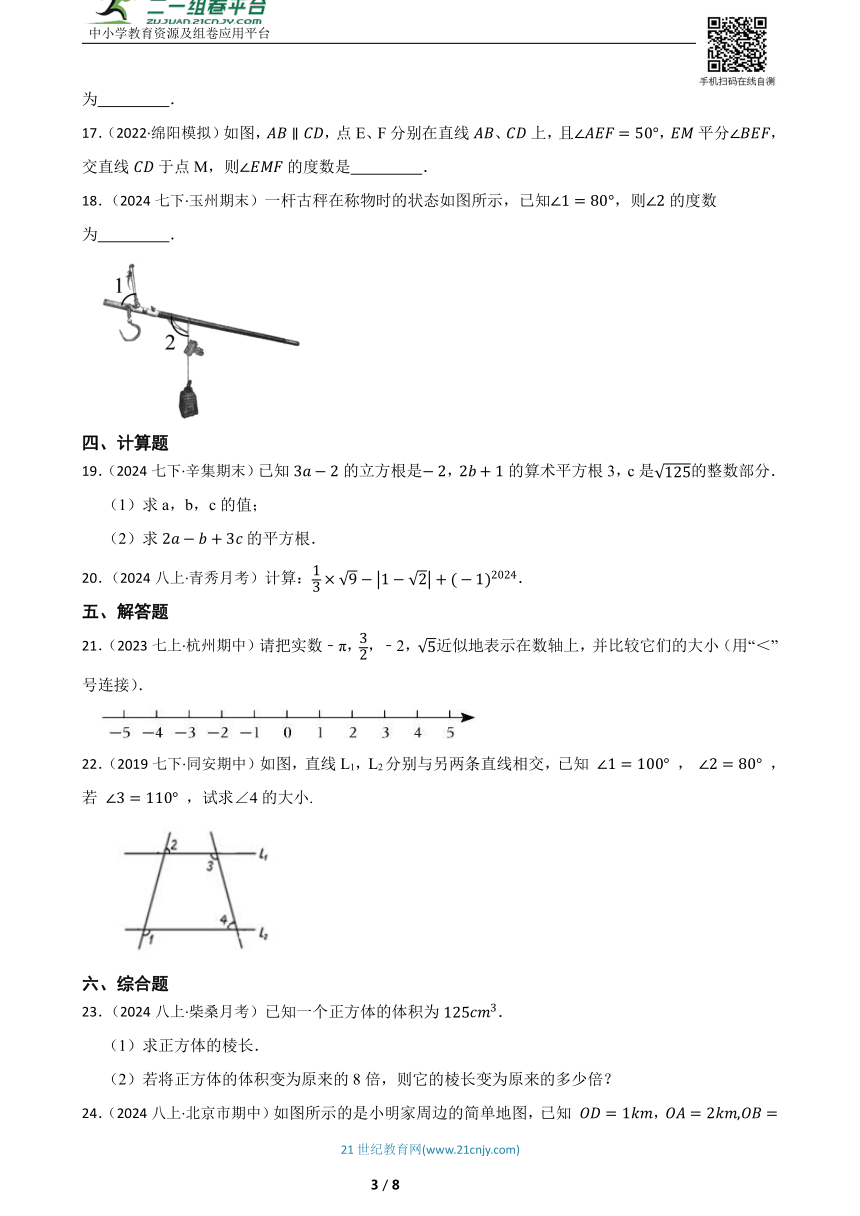
18.(2024七下·玉州期末)一杆古秤在称物时的状态如图所示,已知,则的度数为 .
四、计算题
19.(2024七下·辛集期末)已知的立方根是,的算术平方根3,c是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
20.(2024八上·青秀月考)计算:.
五、解答题
21.(2023七上·杭州期中)请把实数﹣π,,﹣2,近似地表示在数轴上,并比较它们的大小(用“<”号连接).
22.(2019七下·同安期中)如图,直线L1,L2分别与另两条直线相交,已知 , ,若 ,试求∠4的大小.
六、综合题
23.(2024八上·柴桑月考)已知一个正方体的体积为.
(1)求正方体的棱长.
(2)若将正方体的体积变为原来的8倍,则它的棱长变为原来的多少倍?
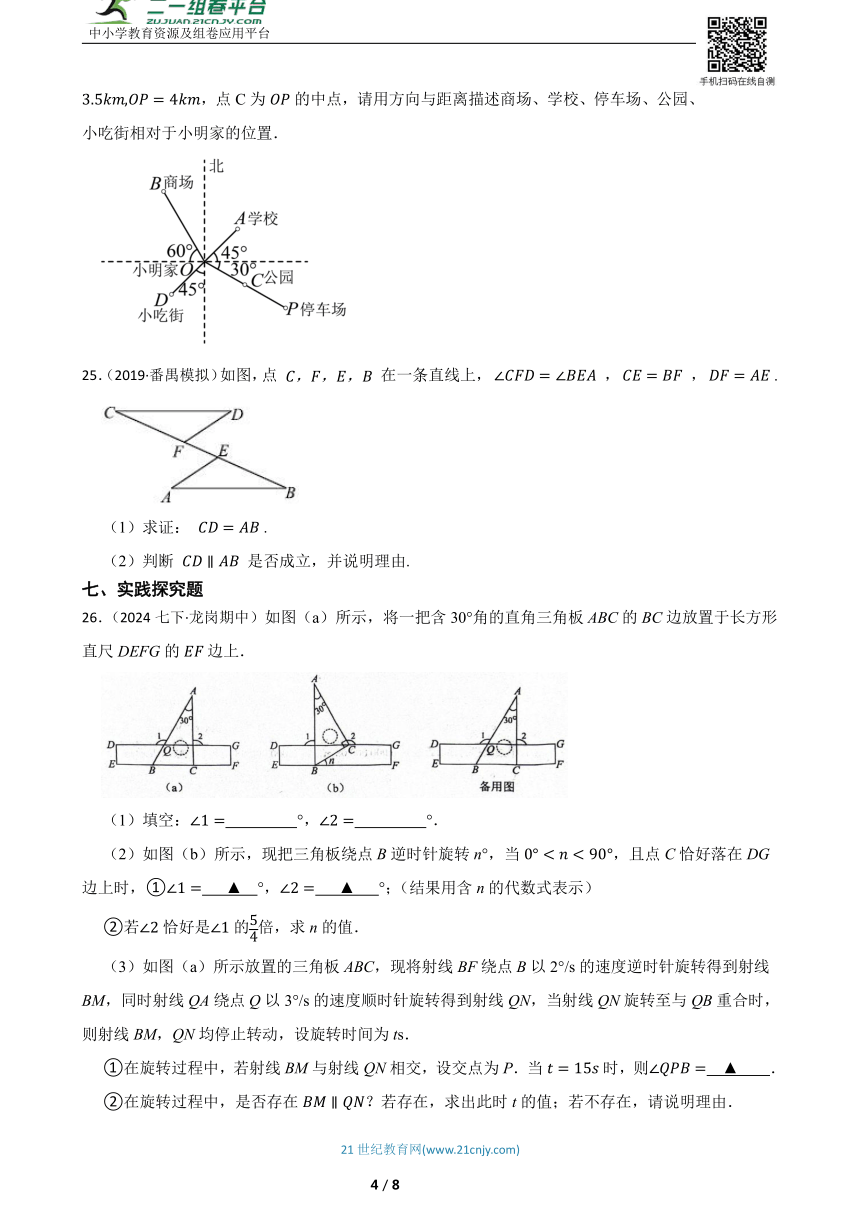
24.(2024八上·北京市期中)如图所示的是小明家周边的简单地图,已知 ,,点C为的中点,请用方向与距离描述商场、学校、停车场、公园、小吃街相对于小明家的位置.
25.(2019·番禺模拟)如图,点 在一条直线上, , , .
(1)求证: .
(2)判断 是否成立,并说明理由.
七、实践探究题
26.(2024七下·龙岗期中)如图(a)所示,将一把含30°角的直角三角板ABC的BC边放置于长方形直尺DEFG的边上.
(1)填空: °, °.
(2)如图(b)所示,现把三角板绕点B逆时针旋转n°,当,且点C恰好落在DG边上时,① ▲ °, ▲ °;(结果用含n的代数式表示)
②若恰好是的倍,求n的值.
(3)如图(a)所示放置的三角板ABC,现将射线BF绕点B以2°/s的速度逆时针旋转得到射线BM,同时射线QA绕点Q以3°/s的速度顺时针旋转得到射线QN,当射线QN旋转至与QB重合时,则射线BM,QN均停止转动,设旋转时间为ts.
①在旋转过程中,若射线BM与射线QN相交,设交点为P.当时,则 ▲ .
②在旋转过程中,是否存在?若存在,求出此时t的值;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】举反例判断命题真假
2.【答案】A
【知识点】等腰三角形的判定与性质;等边三角形的判定;真命题与假命题
3.【答案】D
【知识点】平方根的概念与表示;立方根的概念与表示
4.【答案】B
【知识点】平行线的性质
5.【答案】C
【知识点】用坐标表示地理位置
6.【答案】错误
【知识点】点到直线的距离
7.【答案】错误
【知识点】平行线的判定
8.【答案】(1)正确
(2)正确
(3)错误
(4)正确
(5)正确
(6)正确
(7)错误
(8)正确
【知识点】定义、命题、定理、推论的概念
【答案】9.正确
10.错误
11.错误
12.正确
【知识点】平方根的概念与表示;开平方(求平方根)
13.【答案】
【知识点】开平方(求平方根)
14.【答案】115°
【知识点】角的运算;邻补角
15.【答案】42°
【知识点】平行线的判定与性质
16.【答案】
【知识点】点的坐标;算术平方根的性质(双重非负性);绝对值的非负性
17.【答案】
【知识点】平行线的性质;角平分线的性质
18.【答案】
【知识点】平行线的性质;邻补角
19.【答案】(1),,
(2)
【知识点】无理数的估值;平方根的概念与表示;开平方(求平方根);立方根的概念与表示
20.【答案】
【知识点】有理数的乘方法则;化简含绝对值有理数;求算术平方根
21.【答案】解:所给的四个实数在数轴上表示如下:
由四个实数数轴上表示的位置可知:﹣π<﹣2<<.
【知识点】无理数在数轴上表示;有理数的大小比较-数轴比较法
22.【答案】解:设∠1、∠2对顶角为∠5、∠6,
∠5+∠6=∠1+∠2=180°,
∵∠5、∠6为同旁内错角,
∴直线l1∥直线l2
,
又∵直线l1∥直线l2
∴∠3+∠4=180°,
∴∠4=70°.
【知识点】平行线的判定与性质;对顶角及其性质
23.【答案】(1)
(2)棱长变为原来的2倍
【知识点】立方根的实际应用
24.【答案】商场在小明家西偏北,处;学校在小明家东偏北,处;公园在小明家东偏南,处;停车场在小明家东偏南 ,处;小吃街在小明家南偏西,处
【知识点】用坐标表示地理位置
25.【答案】(1)证明:∵ ,
∴ 即: .
在 和 中,
∴ . ∴
(2)解: 成立.
理由: 由(1)知 ,∴ ,∴
【知识点】平行线的判定;全等三角形的判定与性质
26.【答案】(1)120;90
(2)解:①,
②当时,,解得.∴n的值是.
(3)解:①15°
②存在.理由如下:
情形1:如下图所示,
∵,∴.
∴.解得.
情形2:如图所示,∵,∴.
∴.
解得.
综上所述,t的值为12或48.
【知识点】平行线的判定与性质;图形的旋转
21世纪教育网(www.21cnjy.com)
2 / 9
人教版数学七年级下册期中复习题一【精华】
一、单选题
1.(2024八上·杭州月考)下列选项中,可以用来证明命题“若,则”的逆命题是假命题的反例是( )
A. B. C. D.
2.(2022八上·长春期末)下列命题中的假命题是( )
A.若,则
B.有一个角为的等腰三角形是等边三角形
C.若一个三角形有两个角相等,则这个三角形是等腰三角形
D.等腰三角形底边上的高平分它的顶角
3.(2024八上·深圳期中)下列运算正确的是( )
A. B. C. D.
4.(2024七下·南乐期末)如图,是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , ,则的度数为( )
A. B. C. D.
5.(2024八上·薛城期中)如图是雷达探测到的6个目标,若目标B用表示,目标F用表示,则表示为的目标是( )
A.目标A B.目标C C.目标D D.目标E
二、判断题
6.(2024七下·北京市月考)直线外一点到这条直线的垂线段叫做点到直线的距离
7.(2024七下·北京市月考)判断题:若,,则
8.判断下列语句哪些是命题,哪些不是命题(填“正确”或“错误”).
(1)方程2x-4=0的解是x=2.( )
(2)这朵小花是红色的.( )
(3)在△ABC中,若AB>AC,则∠C>∠B吗 ( )
(4)若ab>0,则a>0.( )
(5)两个相等的同位角的角平分线平行.( )
(6)两个无理数的和必是无理数.( )
(7)请画出一对对顶角.( )
(8)(a为实数).( )
判断题.
9.是5 的一个平方根;
10.的算术平方根是3;
11.的平方根是±2;
12.0的平方根与算术平方根都是0.
三、填空题
13.(2023八下·东昌府期末)的平方根为 .
14.(2024七上·广州期末)如图,是直线上一点,已知,,则 .
15.(2023七下·大竹期末)如图,,垂足为,过作.若,则 .
16.(2023八上·肃州期中)已知,则点关于x轴对称的点的坐标为 .
17.(2022·绵阳模拟)如图,,点E、F分别在直线、上,且,平分,交直线于点M,则的度数是 .
18.(2024七下·玉州期末)一杆古秤在称物时的状态如图所示,已知,则的度数为 .
四、计算题
19.(2024七下·辛集期末)已知的立方根是,的算术平方根3,c是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
20.(2024八上·青秀月考)计算:.
五、解答题
21.(2023七上·杭州期中)请把实数﹣π,,﹣2,近似地表示在数轴上,并比较它们的大小(用“<”号连接).
22.(2019七下·同安期中)如图,直线L1,L2分别与另两条直线相交,已知 , ,若 ,试求∠4的大小.
六、综合题
23.(2024八上·柴桑月考)已知一个正方体的体积为.
(1)求正方体的棱长.
(2)若将正方体的体积变为原来的8倍,则它的棱长变为原来的多少倍?
24.(2024八上·北京市期中)如图所示的是小明家周边的简单地图,已知 ,,点C为的中点,请用方向与距离描述商场、学校、停车场、公园、小吃街相对于小明家的位置.
25.(2019·番禺模拟)如图,点 在一条直线上, , , .
(1)求证: .
(2)判断 是否成立,并说明理由.
七、实践探究题
26.(2024七下·龙岗期中)如图(a)所示,将一把含30°角的直角三角板ABC的BC边放置于长方形直尺DEFG的边上.
(1)填空: °, °.
(2)如图(b)所示,现把三角板绕点B逆时针旋转n°,当,且点C恰好落在DG边上时,① ▲ °, ▲ °;(结果用含n的代数式表示)
②若恰好是的倍,求n的值.
(3)如图(a)所示放置的三角板ABC,现将射线BF绕点B以2°/s的速度逆时针旋转得到射线BM,同时射线QA绕点Q以3°/s的速度顺时针旋转得到射线QN,当射线QN旋转至与QB重合时,则射线BM,QN均停止转动,设旋转时间为ts.
①在旋转过程中,若射线BM与射线QN相交,设交点为P.当时,则 ▲ .
②在旋转过程中,是否存在?若存在,求出此时t的值;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】举反例判断命题真假
2.【答案】A
【知识点】等腰三角形的判定与性质;等边三角形的判定;真命题与假命题
3.【答案】D
【知识点】平方根的概念与表示;立方根的概念与表示
4.【答案】B
【知识点】平行线的性质
5.【答案】C
【知识点】用坐标表示地理位置
6.【答案】错误
【知识点】点到直线的距离
7.【答案】错误
【知识点】平行线的判定
8.【答案】(1)正确
(2)正确
(3)错误
(4)正确
(5)正确
(6)正确
(7)错误
(8)正确
【知识点】定义、命题、定理、推论的概念
【答案】9.正确
10.错误
11.错误
12.正确
【知识点】平方根的概念与表示;开平方(求平方根)
13.【答案】
【知识点】开平方(求平方根)
14.【答案】115°
【知识点】角的运算;邻补角
15.【答案】42°
【知识点】平行线的判定与性质
16.【答案】
【知识点】点的坐标;算术平方根的性质(双重非负性);绝对值的非负性
17.【答案】
【知识点】平行线的性质;角平分线的性质
18.【答案】
【知识点】平行线的性质;邻补角
19.【答案】(1),,
(2)
【知识点】无理数的估值;平方根的概念与表示;开平方(求平方根);立方根的概念与表示
20.【答案】
【知识点】有理数的乘方法则;化简含绝对值有理数;求算术平方根
21.【答案】解:所给的四个实数在数轴上表示如下:
由四个实数数轴上表示的位置可知:﹣π<﹣2<<.
【知识点】无理数在数轴上表示;有理数的大小比较-数轴比较法
22.【答案】解:设∠1、∠2对顶角为∠5、∠6,
∠5+∠6=∠1+∠2=180°,
∵∠5、∠6为同旁内错角,
∴直线l1∥直线l2
,
又∵直线l1∥直线l2
∴∠3+∠4=180°,
∴∠4=70°.
【知识点】平行线的判定与性质;对顶角及其性质
23.【答案】(1)
(2)棱长变为原来的2倍
【知识点】立方根的实际应用
24.【答案】商场在小明家西偏北,处;学校在小明家东偏北,处;公园在小明家东偏南,处;停车场在小明家东偏南 ,处;小吃街在小明家南偏西,处
【知识点】用坐标表示地理位置
25.【答案】(1)证明:∵ ,
∴ 即: .
在 和 中,
∴ . ∴
(2)解: 成立.
理由: 由(1)知 ,∴ ,∴
【知识点】平行线的判定;全等三角形的判定与性质
26.【答案】(1)120;90
(2)解:①,
②当时,,解得.∴n的值是.
(3)解:①15°
②存在.理由如下:
情形1:如下图所示,
∵,∴.
∴.解得.
情形2:如图所示,∵,∴.
∴.
解得.
综上所述,t的值为12或48.
【知识点】平行线的判定与性质;图形的旋转
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
