第17章 勾股定理 素养培优测试题(含答案)
文档属性
| 名称 | 第17章 勾股定理 素养培优测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-21 04:47:09 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第17章 勾股定理 素养培优测试题
考试范围:第17章 勾股定理;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.下列各组数中,是勾股数的一组是( )
A.0.3,0.4,0.5 B.,,
C.32,42,52 D.9,40,41
2.将等腰直角三角板ABC按如图的方式放置,点A在x轴的正半轴上移动,点B随之在y轴的正半轴上移动,点C在AB的左侧,设点C的横坐标为﹣2,则它的纵坐标为( )
A.﹣2 B.2 C. D.
(2题) (4题) (5题) (6题)
3.下列命题的逆命题成立的是( )
A.对顶角相等 B.全等三角形的对应角相等
C.等腰三角形两底角相等 D.如果两数相等,那么它们的绝对值相等
4.如图是由边长为1的小正方形组成的网格,△ABC的顶点A,B,C均在格点上.若AD⊥BC于点D,则线段AD的长为( )
A. B.2 C.1 D.2
5.“赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的长直角边是12,大正方形的面积是169,则小正方形的面积是( )
A.25 B.36 C.49 D.64
6.如图,在四边形OABC中,∠A=∠CBO=90°,AB=BC=1,∠AOB=30°,则点B到OC的距离为( )
A. B. C.1 D.2
7.甲、乙两艘客轮同时离开港口,航行速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东60°的方向航行,则乙客轮的航行方向可能是( )
A.北偏西60° B.南偏西60° C.南偏西30° D.南偏东30°
8.下列条件中,不能判定△ABC是直角三角形的是( )
A.∠A=∠B+∠C B.∠A:∠B:∠C=3:4:5
C.a2=(b+c)(b﹣c) D.a:b:c=7:24:25
9.如图,一根长为25m的梯子AB斜靠在垂直于地面的墙上,这时梯子的底端B离墙根E的距离为7m,如果梯子的底端向外(远离墙根方向)移动8m至D处则梯子的顶端将沿墙向下移动的距离AC为( )
A.4m B.5m C.8m D.7m
10.如图,△OA1A2是等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3,再以OA3为直角边作等腰直角三角形OA3A4,…,按此规律作下去,则OA2021的长为( )
A. B.
C. D.
(9题) (10题) (11题) (12题)
二.填空题(共5小题,满分15分,每小题3分)
11.如图,已知四边形ABCD中,∠B=90°,AB=4,BC=3,AD=12,DC=13,则四边形ABCD的面积为 .
12.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.其中,b+a=12,则中间小正方形的面积是 .
13.在直角△ABC中,∠ACB=90°,AC=6,BC=8,如果AB的中线CD上有个点E,使,那么AE= .
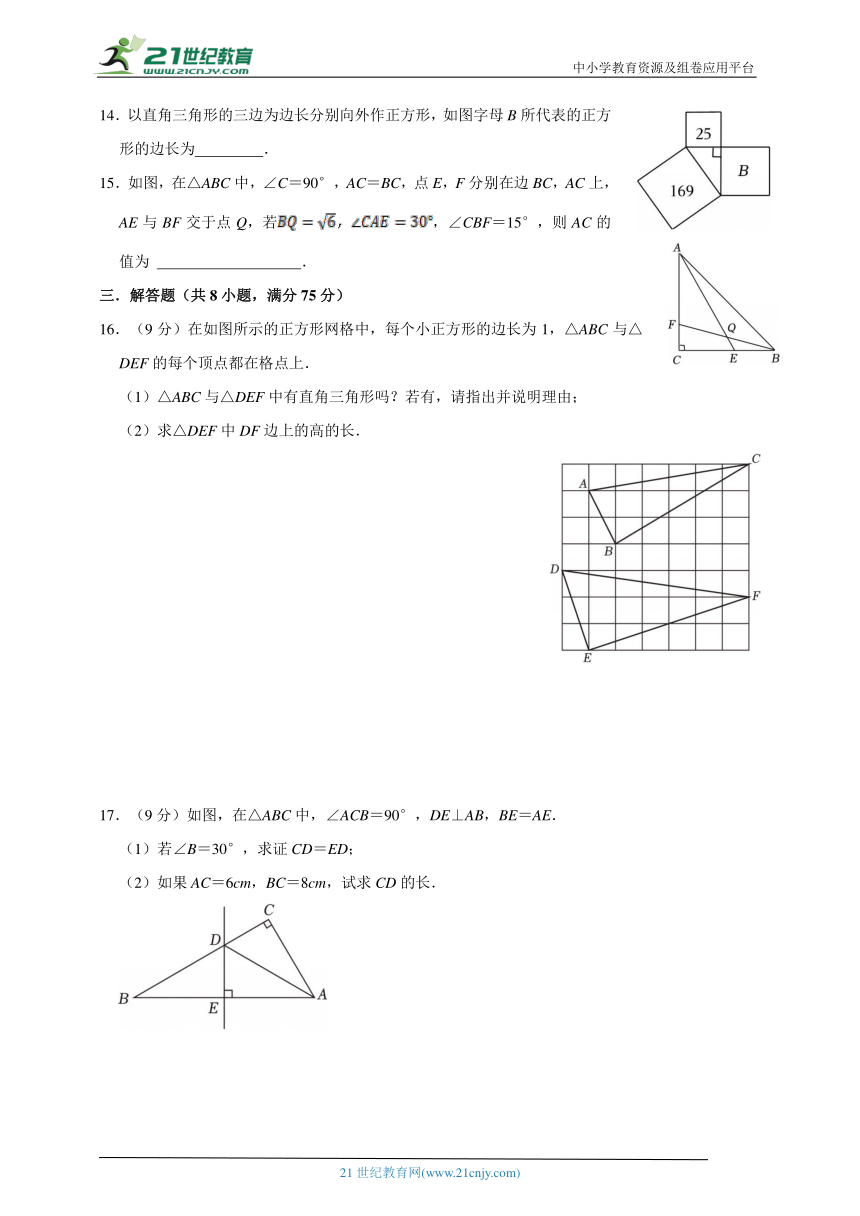
14.以直角三角形的三边为边长分别向外作正方形,如图字母B所代表的正方形的边长为 .
15.如图,在△ABC中,∠C=90°,AC=BC,点E,F分别在边BC,AC上,AE与BF交于点Q,若,∠CBF=15°,则AC的值为 .
三.解答题(共8小题,满分75分)
16.(9分)在如图所示的正方形网格中,每个小正方形的边长为1,△ABC与△DEF的每个顶点都在格点上.
(1)△ABC与△DEF中有直角三角形吗?若有,请指出并说明理由;
(2)求△DEF中DF边上的高的长.
17.(9分)如图,在△ABC中,∠ACB=90°,DE⊥AB,BE=AE.
(1)若∠B=30°,求证CD=ED;
(2)如果AC=6cm,BC=8cm,试求CD的长.
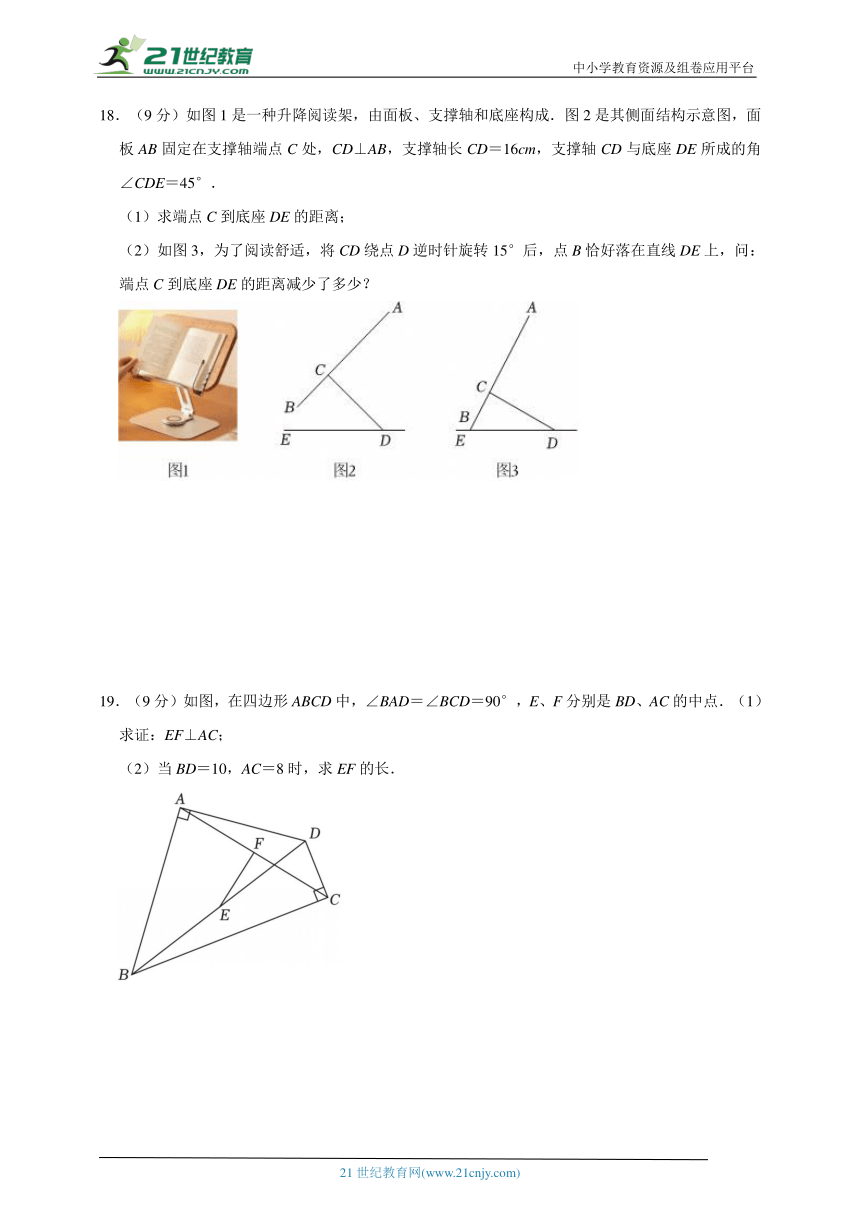
18.(9分)如图1是一种升降阅读架,由面板、支撑轴和底座构成.图2是其侧面结构示意图,面板AB固定在支撑轴端点C处,CD⊥AB,支撑轴长CD=16cm,支撑轴CD与底座DE所成的角∠CDE=45°.
(1)求端点C到底座DE的距离;
(2)如图3,为了阅读舒适,将CD绕点D逆时针旋转15°后,点B恰好落在直线DE上,问:端点C到底座DE的距离减少了多少?
19.(9分)如图,在四边形ABCD中,∠BAD=∠BCD=90°,E、F分别是BD、AC的中点.(1)求证:EF⊥AC;
(2)当BD=10,AC=8时,求EF的长.
20.(9分)(1)【问题】如图1,△ABC中,∠BAC=120°,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转120°得到AE,连接EC,DE,则线段BD,EC之间满足的数量关系式为 ;直线BD,EC相交所夹的锐角的度数为 ;
(2)【探索】如图2,△ABC中,∠BAC=120°,AB=AC,D为△ABC外一点,将线段AD绕点A逆时针旋转120°得到AE,连接EC,DE,延长BD,EC交于点F.试问:(1)中的结论是否成立?若成立,请证明,若不成立,请说明理由;
(3)【应用】在(2)的条件下,,,求四边形ABFC的面积.
21.(9分)问题提出:
(1)如图1,直线AB,CD被EG所截,且AB∥CD,GF平分∠EGC,EF平分∠AEG.求∠EFG的度数.
问题解决:
(2)如图2,某中学有一块四边形ABCD的空地,其中AD∥BC,DC⊥BC,∠ABC与∠BAD的平分线交于点P,且PA=6m,CD=PB=6m,AB=BC=12m,且AD的长度是点P到AB距离的倍.为了更好的落实“双减”政策,丰富孩子们的课业生活,学校计划将该四边形空地改造成多功能区域,现要求将三角形APB区域设计成手工制作区,五边形ADCBP设计成健身区,求健身区的面积.(参考公式:三角形的面积=底×高÷2)
22.(10分)如图,在△ABC中,∠C=90°,把△ABC沿直线DE折叠,使△ADE与△BDE重合.
(1)若∠A=38°,则∠CBD的度数为 ;
(2)若AC=6,BC=4,求AD的长;
(3)当AB=m(m>0),△ABC的面积为2m+4时,求△BCD的周长.(用含m的代数式表示)
23.(11分)阅读与思考
下面是莉莉同学的数学学习笔记的部分内容.请仔细阅读,并完成相应的任务.
巧求三角形的面积例题:在△ABC中,AB,BC,AC三边的长分别为,,,求△ABC的面积.解法:如果直接运用公式(a为底边,h为对应的高)求解,那么高h的求解较复杂.进一步观察可发现.由 (依据1)可知,,1,2构成的三角形为直角三角形,所以可将AB转化为直角边为1和2的直角三角形的斜边;同理,BC可转化为直角边为1和3的直角三角形的斜边;AC可转化为直角边为2和3的直角三角形的斜边.由 (依据2),可把△ABC放到如图1的正方形网格中(每个小正方形的边长为1),且△ABC的三个顶点恰好都在小正方形的顶点处,这样无需求三角形的高,直接借助网格就能计算出△ABC的面积.启发:如图2,△PMN的三边MN,PN,PM的长分别为,,.请利用图2的正方形网格(每个小正方形的边长均为1),画出相应的△PMN.
任务:
(1)材料中的依据1是指 (填“A”或“B”).依据2是指 (填“C”或“D”).
A.两个锐角互余的三角形为直角三角形 B.勾股定理的逆定理
C.数形结合思想 D.分类讨论思想
(2)画出“启发”中的△PMN.
(3)求△PMN的面积.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、0.3,0.4,0.5都不是正整数,本选项中一组数据不是勾股数,不符合题意;
B、,,不都是正整数,本选项中一组数据不是勾股数,不符合题意;
C、∵(32)2+(42)2=81+256=337,(52)2=625,
∴(32)2+(42)2≠(52)2,
∴本选项中一组数据不是勾股数,不符合题意;
D、∵92+402=81+1600=1681,412=1681,
∴92+402=412,
∴正整数9,40,41是勾股数,符合题意;
故选:D.
2.解:作CD⊥x轴于点D,CE⊥y轴于点E,如图,
则∠CDA=∠CEB=90°,
∵△ABC是等腰直角三角形,
∴∠BCA=90°,BC=AC,
∴∠BCE+∠ECA=90°,
又∵∠BCE+∠CBE=90°,
∴∠ECA=∠CBE,
∵CE∥DA,
∴∠CAD=∠ECA,
∴∠CAD=∠CBE,
在△CBE和△CAD中,
,
∴△CBE≌△CAD(AAS),
∴CE=CD,
∵点C的横坐标为﹣2,
∴它的纵坐标为2,
故选:B.
3.解:A、逆命题为:相等的角为对顶角,错误,不成立,不符合题意;
B、逆命题为:对应角相等的三角形全等,错误,不成立,不符合题意;
C、逆命题为:两角相等的三角形是等腰三角形,正确,成立,符合题意;
D、逆命题为:绝对值相等的两个数相等,错误,不成立,不符合题意;
故选:C.
4.解:由勾股定理得:AC2=22+12=5,AB2=22+42=20,BC2=32+42=25,
∴AC,AB=2,BC=5,
∵AC2+AB2=BC2,
∴△ABC是直角三角形,
∵AD⊥BC,
∴△ABC的面积AC ABBC AD,
∴25AD,
∴AD=2.
故选:D.
5.解:设大正方形的边长为c,直角三角形的小直角边为a,
∵大正方形的面积是169,
∴c=13,
∵直角三角形的长直角边是12,
∴a5,
∴小正方形的边长=12﹣5=7,
∴小正方形的面积=49.
故选:C.
6.解:作BH⊥OC于H,
∵∠AOB=30°,∠A=90°,
∴OB=2AB=2,
在Rt△OBC中,由勾股定理得,
OC,
∵∠CBO=∠BHC=90°,
∴∠CBH=∠BOC,
∴BH,
故选:B.
7.解:依照题意画出图形,
甲的路程PA=40×15=600(m),乙的路程PB=20×40=800(m),AB=1000m,
∵6002+8002=10002,
∴PA2+PB2=AB2,
∴△APB为直角三角形,且∠APB=90°.
∵∠NPA=60°,
∴∠SPB=∠NPB′=30°,
∴乙客轮的航行方向为南偏东30°或北偏西30°,
∴乙客轮的航行方向可能是南偏东30°,
故选:D.
8.解:A、∵∠A=∠B+∠C,∠A+∠B+∠C=180°,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意;
B.∴∠A:∠B:∠C=3:4:5,
∴∠C=180°75°,
∴△ABC不是直角三角形,符合题意;
C、∵a2=(b+c)(b﹣c),
∴a2=b2﹣c2,
∴a2+c2=b2,
∴△ABC是直角三角形,不符合题意;
D、∵a:b:c=7:24:25,
∴设a=7k,b=24k,c=25k,
∵a2+b2=(7k)2+(24k)2=(25k)2=c2,
∴△ABC是直角三角形,不符合题意;
故选:B.
9.解:由题意得:BE=7m,AB=CD=25m,BD=8m,
∴DE=BE+BD=15,
在Rt△AEB中,
(m),
在Rt△CED中,(m),
∴AC=AE﹣CE=4m,
故选:A.
10.解:∵△OA1A2为等腰直角三角形,OA1=1,
∴OA2,
∵△OA2A3为等腰直角三角形,
∴OA3=2=()2;
∵△OA3A4为等腰直角三角形,
∴OA4=2()3.
∵△OA4A5为等腰直角三角形,
∴OA5=4=()4,
……
∴OA2021的长为()2021﹣1=()2020,
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:连接AC,
∵AB=4,BC=3,AD=12,DC=13,∠B=90°,
∴在直角三角形ABC中有:BC2+AB2=AC2,即AC2=9+16=25,
∴AC=5,
又∵AD2=144,DC2=169,
∴AC2+AD2=144+25=169=DC2,即DC2=AC2+AD2,
∴三角形ACD是直角三角形,∠CAD=90°,
∴S四边形ABCD=S△ABC+S△CADBC×BAAC×AD3×45×12=6+30=36.
故答案为:36.
12.解:由勾股定理,得a2+b2=c2=(3)2=90,
∵b+a=12,
∴b2+2ab+a2=144,
∴90+2ab=144,
∴ab=27,四个直角三角形的面积为4ab=54,
∴中间小正方形的面积是90﹣54=36.
故答案为:36.
13.解:∵∠ACB=90°,AC=6,BC=8,
∴AB10,S△ABC6×8=24,
∵CD是Rt△ABC的斜边AB上的中线,
∴CD=AD=BDAB=5,S△ACD=S△BCDS△ABC=12,
作AH⊥CD于点H,则∠AHC=90°,
∵S△ACD5AH=12,
∴AH,
∴CH,
∵CE,
∴EH=CH﹣CE,
∴AE,
故答案为:.
14.解:如图,
由题意得:∠CAD=90°,CD2=25,CD2=169,
∴AD2=CD2﹣AC2=144,
∴AD=12或﹣12(不合题意,舍去),
∴字母B所代表的正方形的边长为12,
故答案为:12.
15.解:方法一:过点Q作QH⊥AB于点H,在HA上截取HD=HB,连接QD,如图所示:
∴QH是线段BD的垂直平分线,
∴QD=QB,
在△ABC中,∠C=90°,AC=BC,
∵∠CAB=∠CBA=45°,
∴∠CAE=30°,∠CBF=15°,
∴∠QAB=∠CAB﹣∠CAE=15°,∠QBA=∠CBA﹣∠CBF=30°,
在Rt△BQH中,∠QBA=30°,QB,
∴QHBQ,
由勾股定理得:BH,
∴HD=HB,
∴DB=DH+HB=3,
∵QD=QB,
∴∠QDB=∠QBA=30°,
∵∠QDB是△DAQ的外角,
∴∠QDB=∠QAB+∠DQA,
∴∠DQA=∠QDB﹣∠QAB=30°﹣15°=15°,
∴∠DQA=∠QAB=15°,
∴AD=QD,
∴AB=AD+DB=3,
∴ACAB=3,
方法二:过B作BM⊥AE交直线AE于M,连接CM,
∵∠C=90°,AC=BC,
∴∠CAB=∠CBA=45°,
∵∠CAE=30°,
∴∠AEB=∠CAE+∠C=120°,
∴∠AEC=∠BEM=60°,
∵∠CBF=15°,
∴∠BQE=180°﹣∠AEB﹣∠CBF=45°,
∵BM⊥AE,
∴∠BMQ=90°,∠BQM=∠QBM=45°,
∴QM=BM,,
∴,
∴∠EBM=90°﹣∠BEM=30°,
∴BE=2EM,
∵BE2=EM2+BM2,
∴,
解得BE=2(负值已舍去),
∴CE=BC﹣BE=AC﹣2,
∵∠CAE=30°,
∴AE=2CE,
Rt△ACE中,AE2=AC2+CE2,
∴(2CE)2=CE+AC2,
解得(负值已舍去),
∴,
解得;
故答案为:3.
三.解答题(共8小题,满分75分)
16.解:(1)△DEF是直角三角形,理由如下:
由勾股定理得:AB2=22+12=5,BC2=52+32=34,AC2=62+12=37,DE2=32+12=10,EF2=62+22=40,DF2=72+12=50,
∵5+34=39≠37,
∴AB2+BC2≠AC2,
∴△ABC不是直角三角形,
∵10+40=50,
∴DE2+EF2=DF2,
∴△DEF是直角三角形;
(2)设△DEF中DF边上的高的长为h,
∵S△DEFDE EFDF h,
∴DE2 EF2=DF2 h2,
∴h28,
∴h2,
答:△DEF中DF边上的高的长为2.
17.(1)证明:∵△ABC中∠B=30°,∠ACB=90°,
∴∠BAC=90°﹣30°=60°,
根据题意可得:DE垂直平分AB,
∴B D=A D,A C=18,B C=12,
∴∠DAB=∠B=30°,
∴∠DAC=60°﹣30°=30°,
∴AD平分∠BAC,
∵DE⊥AB,DC⊥AC,
∴CD=ED.
(2)解:根据解析(1)可知,AD=BD,
设CD=x cm,则AD=BD=(8﹣x)cm,
∵在Rt△ACD中,AD2=CD2+AC2,
则(8﹣x)2=x2+62,
解得:,
即CD的长为.
18.解:(1)如图2,过点C作CF⊥DE于点F,
∵∠CDE=45°,
∴△CFD是等腰直角三角形,
∴CF=DF,
在Rt△CFD中,由勾股定理得:CF2+DF2=CD2,
∴2CF2=CD2=162,
∴CF=8(cm)(负值已舍去);
(2)如图3,过点C作CH⊥DE于点H,
∵将CD绕点D逆时针旋转15°后,点B恰好落在直线DE上,
∴∠CDE=45°﹣15°=30°,
∴CHCD16=8(cm),
∴端点C到底座DE的距离减少了(88)cm.
19.(1)证明:连接AE、CE,
∵∠BAD=90°,E为BD中点,
∴AEDB,
∵∠DCB=90°,
∴CEDB,
∴AE=CE,
∵F是AC中点,
∴EF⊥AC;
(2)解:∵AC=8,BD=10,E、F分别是边AC、BD的中点,
∴AE=CE=5,CF=4,
∵EF⊥AC.
∴EF3.
20.解:(1)∵∠BAC=120°,AB=AC,
∴∠B=∠ACB=30°,
由旋转的性质得:AD=AE,∠DAE=120°,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE=30°,
∴∠BCE=∠ACB+∠ACE=30°+30°=60°,
故答案为:BD=EC,60°,
(2)(1)中的结论成立,证明如下:
∵∠BAC=120°,AB=AC,
∴∠B=∠ACB=30°,
由旋转的性质得:AD=AE,∠DAE=120°,
∴∠AED=∠ADE=30°,∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴BD=EC,∠ADB=∠AEC,
∵∠ADB+∠ADF=180°,
∴∠AEC+∠ADF=180°,
即∠DEF+∠AED+∠ADE+∠EDF=180°,
∴∠DEF+∠EDF=180°﹣30°﹣30°=120°,
∴∠F=180°﹣(∠DEF+∠EDF)=180°﹣120°=60°;
(3)如图2,过点E作EG⊥DF于点G,
则∠EGF=∠EGD=90°,
由(2)可知,△ABD≌△ACE,∠F=60°,
∴S△ABD=S△ACE,∠EGF=90°﹣∠F=30°,
∴S四边形ABFC=S四边形ADFE,GFEF42,
∴EG6,DG=DF﹣GF=8+228,
∴DE10,
过点A作AH⊥DE于点H,
则DH=EHDE=5,∠AHD=90°,
∵∠ADE=30°,
∴AD=2AH,
∴DHAH=5,
∴AH,
∴S四边形ABFC=S四边形ADFE=S△ADE+S△DEFDE AHDF EG10(8+2)×624+624.
21.解:(1)∵AB∥CD,
∴∠EGC=∠BEG,
∵GF平分∠EGC,EF平分∠AEG,
∴∠FEG+∠FGE∠AEG∠EGC(∠AEG+BEG)90°,
∴∠EFG=180°﹣(∠FEG+∠FGE)=180°﹣90°=90°;
(2)由(1)知∠P=90°,
即△ABP是直角三角形,
∴S△ABP618(m2)
∴点P到AB距离为:182÷12=3(m),
∵AD的长度是点P到AB距离的倍,
∴AD=39(m),
∴S梯形ABCD(AD+BC)×CD(6+12)×654(m2),
∴健身区的面积为541836(m2),
答:健身区的面积为36m2.
22.解:(1)∵DE垂直平分AB,
∴DA=DB,
∴∠A=∠DBA=38°;
∵∠C=90°,
∴∠CBD=180°﹣90°﹣76°=14°.
故答案为:14°;
(2)设DA=DB=λ,则DC=6﹣λ;
由勾股定理得:λ2=(6﹣λ)2+42,
解得:λ,
即AD的长为.
(3)∵△ABC的面积为2m+4,
∴AC BC=2(2m+4);
∵AB=m,
∴AC2+BC2=m2,
∴(AC+BC)2=AC2+BC2+2AC BC=m2+4(2m+4)=(m+4)2,
∴AC+BC=m+4(负值已舍去),
∴△BCD的周长=CD+BD+BC=AC+BC=m+4.
23.解:(1)由知,这是利用勾股定理的逆定理,即依据1是勾股定理是逆定理;依据2是数形结合思想的运用;
故答案为:B;C;
(2)补全图形如下:
(3)
=8﹣1﹣2﹣2=3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第17章 勾股定理 素养培优测试题
考试范围:第17章 勾股定理;考试时间:100分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共10小题,满分30分,每小题3分)
1.下列各组数中,是勾股数的一组是( )
A.0.3,0.4,0.5 B.,,
C.32,42,52 D.9,40,41
2.将等腰直角三角板ABC按如图的方式放置,点A在x轴的正半轴上移动,点B随之在y轴的正半轴上移动,点C在AB的左侧,设点C的横坐标为﹣2,则它的纵坐标为( )
A.﹣2 B.2 C. D.
(2题) (4题) (5题) (6题)
3.下列命题的逆命题成立的是( )
A.对顶角相等 B.全等三角形的对应角相等
C.等腰三角形两底角相等 D.如果两数相等,那么它们的绝对值相等
4.如图是由边长为1的小正方形组成的网格,△ABC的顶点A,B,C均在格点上.若AD⊥BC于点D,则线段AD的长为( )
A. B.2 C.1 D.2
5.“赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形,若图中的直角三角形的长直角边是12,大正方形的面积是169,则小正方形的面积是( )
A.25 B.36 C.49 D.64
6.如图,在四边形OABC中,∠A=∠CBO=90°,AB=BC=1,∠AOB=30°,则点B到OC的距离为( )
A. B. C.1 D.2
7.甲、乙两艘客轮同时离开港口,航行速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东60°的方向航行,则乙客轮的航行方向可能是( )
A.北偏西60° B.南偏西60° C.南偏西30° D.南偏东30°
8.下列条件中,不能判定△ABC是直角三角形的是( )
A.∠A=∠B+∠C B.∠A:∠B:∠C=3:4:5
C.a2=(b+c)(b﹣c) D.a:b:c=7:24:25
9.如图,一根长为25m的梯子AB斜靠在垂直于地面的墙上,这时梯子的底端B离墙根E的距离为7m,如果梯子的底端向外(远离墙根方向)移动8m至D处则梯子的顶端将沿墙向下移动的距离AC为( )
A.4m B.5m C.8m D.7m
10.如图,△OA1A2是等腰直角三角形,OA1=1,以斜边OA2为直角边作等腰直角三角形OA2A3,再以OA3为直角边作等腰直角三角形OA3A4,…,按此规律作下去,则OA2021的长为( )
A. B.
C. D.
(9题) (10题) (11题) (12题)
二.填空题(共5小题,满分15分,每小题3分)
11.如图,已知四边形ABCD中,∠B=90°,AB=4,BC=3,AD=12,DC=13,则四边形ABCD的面积为 .
12.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.其中,b+a=12,则中间小正方形的面积是 .
13.在直角△ABC中,∠ACB=90°,AC=6,BC=8,如果AB的中线CD上有个点E,使,那么AE= .
14.以直角三角形的三边为边长分别向外作正方形,如图字母B所代表的正方形的边长为 .
15.如图,在△ABC中,∠C=90°,AC=BC,点E,F分别在边BC,AC上,AE与BF交于点Q,若,∠CBF=15°,则AC的值为 .
三.解答题(共8小题,满分75分)
16.(9分)在如图所示的正方形网格中,每个小正方形的边长为1,△ABC与△DEF的每个顶点都在格点上.
(1)△ABC与△DEF中有直角三角形吗?若有,请指出并说明理由;
(2)求△DEF中DF边上的高的长.
17.(9分)如图,在△ABC中,∠ACB=90°,DE⊥AB,BE=AE.
(1)若∠B=30°,求证CD=ED;
(2)如果AC=6cm,BC=8cm,试求CD的长.
18.(9分)如图1是一种升降阅读架,由面板、支撑轴和底座构成.图2是其侧面结构示意图,面板AB固定在支撑轴端点C处,CD⊥AB,支撑轴长CD=16cm,支撑轴CD与底座DE所成的角∠CDE=45°.
(1)求端点C到底座DE的距离;
(2)如图3,为了阅读舒适,将CD绕点D逆时针旋转15°后,点B恰好落在直线DE上,问:端点C到底座DE的距离减少了多少?
19.(9分)如图,在四边形ABCD中,∠BAD=∠BCD=90°,E、F分别是BD、AC的中点.(1)求证:EF⊥AC;
(2)当BD=10,AC=8时,求EF的长.
20.(9分)(1)【问题】如图1,△ABC中,∠BAC=120°,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转120°得到AE,连接EC,DE,则线段BD,EC之间满足的数量关系式为 ;直线BD,EC相交所夹的锐角的度数为 ;
(2)【探索】如图2,△ABC中,∠BAC=120°,AB=AC,D为△ABC外一点,将线段AD绕点A逆时针旋转120°得到AE,连接EC,DE,延长BD,EC交于点F.试问:(1)中的结论是否成立?若成立,请证明,若不成立,请说明理由;
(3)【应用】在(2)的条件下,,,求四边形ABFC的面积.
21.(9分)问题提出:
(1)如图1,直线AB,CD被EG所截,且AB∥CD,GF平分∠EGC,EF平分∠AEG.求∠EFG的度数.
问题解决:
(2)如图2,某中学有一块四边形ABCD的空地,其中AD∥BC,DC⊥BC,∠ABC与∠BAD的平分线交于点P,且PA=6m,CD=PB=6m,AB=BC=12m,且AD的长度是点P到AB距离的倍.为了更好的落实“双减”政策,丰富孩子们的课业生活,学校计划将该四边形空地改造成多功能区域,现要求将三角形APB区域设计成手工制作区,五边形ADCBP设计成健身区,求健身区的面积.(参考公式:三角形的面积=底×高÷2)
22.(10分)如图,在△ABC中,∠C=90°,把△ABC沿直线DE折叠,使△ADE与△BDE重合.
(1)若∠A=38°,则∠CBD的度数为 ;
(2)若AC=6,BC=4,求AD的长;
(3)当AB=m(m>0),△ABC的面积为2m+4时,求△BCD的周长.(用含m的代数式表示)
23.(11分)阅读与思考
下面是莉莉同学的数学学习笔记的部分内容.请仔细阅读,并完成相应的任务.
巧求三角形的面积例题:在△ABC中,AB,BC,AC三边的长分别为,,,求△ABC的面积.解法:如果直接运用公式(a为底边,h为对应的高)求解,那么高h的求解较复杂.进一步观察可发现.由 (依据1)可知,,1,2构成的三角形为直角三角形,所以可将AB转化为直角边为1和2的直角三角形的斜边;同理,BC可转化为直角边为1和3的直角三角形的斜边;AC可转化为直角边为2和3的直角三角形的斜边.由 (依据2),可把△ABC放到如图1的正方形网格中(每个小正方形的边长为1),且△ABC的三个顶点恰好都在小正方形的顶点处,这样无需求三角形的高,直接借助网格就能计算出△ABC的面积.启发:如图2,△PMN的三边MN,PN,PM的长分别为,,.请利用图2的正方形网格(每个小正方形的边长均为1),画出相应的△PMN.
任务:
(1)材料中的依据1是指 (填“A”或“B”).依据2是指 (填“C”或“D”).
A.两个锐角互余的三角形为直角三角形 B.勾股定理的逆定理
C.数形结合思想 D.分类讨论思想
(2)画出“启发”中的△PMN.
(3)求△PMN的面积.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、0.3,0.4,0.5都不是正整数,本选项中一组数据不是勾股数,不符合题意;
B、,,不都是正整数,本选项中一组数据不是勾股数,不符合题意;
C、∵(32)2+(42)2=81+256=337,(52)2=625,
∴(32)2+(42)2≠(52)2,
∴本选项中一组数据不是勾股数,不符合题意;
D、∵92+402=81+1600=1681,412=1681,
∴92+402=412,
∴正整数9,40,41是勾股数,符合题意;
故选:D.
2.解:作CD⊥x轴于点D,CE⊥y轴于点E,如图,
则∠CDA=∠CEB=90°,
∵△ABC是等腰直角三角形,
∴∠BCA=90°,BC=AC,
∴∠BCE+∠ECA=90°,
又∵∠BCE+∠CBE=90°,
∴∠ECA=∠CBE,
∵CE∥DA,
∴∠CAD=∠ECA,
∴∠CAD=∠CBE,
在△CBE和△CAD中,
,
∴△CBE≌△CAD(AAS),
∴CE=CD,
∵点C的横坐标为﹣2,
∴它的纵坐标为2,
故选:B.
3.解:A、逆命题为:相等的角为对顶角,错误,不成立,不符合题意;
B、逆命题为:对应角相等的三角形全等,错误,不成立,不符合题意;
C、逆命题为:两角相等的三角形是等腰三角形,正确,成立,符合题意;
D、逆命题为:绝对值相等的两个数相等,错误,不成立,不符合题意;
故选:C.
4.解:由勾股定理得:AC2=22+12=5,AB2=22+42=20,BC2=32+42=25,
∴AC,AB=2,BC=5,
∵AC2+AB2=BC2,
∴△ABC是直角三角形,
∵AD⊥BC,
∴△ABC的面积AC ABBC AD,
∴25AD,
∴AD=2.
故选:D.
5.解:设大正方形的边长为c,直角三角形的小直角边为a,
∵大正方形的面积是169,
∴c=13,
∵直角三角形的长直角边是12,
∴a5,
∴小正方形的边长=12﹣5=7,
∴小正方形的面积=49.
故选:C.
6.解:作BH⊥OC于H,
∵∠AOB=30°,∠A=90°,
∴OB=2AB=2,
在Rt△OBC中,由勾股定理得,
OC,
∵∠CBO=∠BHC=90°,
∴∠CBH=∠BOC,
∴BH,
故选:B.
7.解:依照题意画出图形,
甲的路程PA=40×15=600(m),乙的路程PB=20×40=800(m),AB=1000m,
∵6002+8002=10002,
∴PA2+PB2=AB2,
∴△APB为直角三角形,且∠APB=90°.
∵∠NPA=60°,
∴∠SPB=∠NPB′=30°,
∴乙客轮的航行方向为南偏东30°或北偏西30°,
∴乙客轮的航行方向可能是南偏东30°,
故选:D.
8.解:A、∵∠A=∠B+∠C,∠A+∠B+∠C=180°,
∴∠A=90°,
∴△ABC是直角三角形,不符合题意;
B.∴∠A:∠B:∠C=3:4:5,
∴∠C=180°75°,
∴△ABC不是直角三角形,符合题意;
C、∵a2=(b+c)(b﹣c),
∴a2=b2﹣c2,
∴a2+c2=b2,
∴△ABC是直角三角形,不符合题意;
D、∵a:b:c=7:24:25,
∴设a=7k,b=24k,c=25k,
∵a2+b2=(7k)2+(24k)2=(25k)2=c2,
∴△ABC是直角三角形,不符合题意;
故选:B.
9.解:由题意得:BE=7m,AB=CD=25m,BD=8m,
∴DE=BE+BD=15,
在Rt△AEB中,
(m),
在Rt△CED中,(m),
∴AC=AE﹣CE=4m,
故选:A.
10.解:∵△OA1A2为等腰直角三角形,OA1=1,
∴OA2,
∵△OA2A3为等腰直角三角形,
∴OA3=2=()2;
∵△OA3A4为等腰直角三角形,
∴OA4=2()3.
∵△OA4A5为等腰直角三角形,
∴OA5=4=()4,
……
∴OA2021的长为()2021﹣1=()2020,
故选:B.
二.填空题(共5小题,满分15分,每小题3分)
11.解:连接AC,
∵AB=4,BC=3,AD=12,DC=13,∠B=90°,
∴在直角三角形ABC中有:BC2+AB2=AC2,即AC2=9+16=25,
∴AC=5,
又∵AD2=144,DC2=169,
∴AC2+AD2=144+25=169=DC2,即DC2=AC2+AD2,
∴三角形ACD是直角三角形,∠CAD=90°,
∴S四边形ABCD=S△ABC+S△CADBC×BAAC×AD3×45×12=6+30=36.
故答案为:36.
12.解:由勾股定理,得a2+b2=c2=(3)2=90,
∵b+a=12,
∴b2+2ab+a2=144,
∴90+2ab=144,
∴ab=27,四个直角三角形的面积为4ab=54,
∴中间小正方形的面积是90﹣54=36.
故答案为:36.
13.解:∵∠ACB=90°,AC=6,BC=8,
∴AB10,S△ABC6×8=24,
∵CD是Rt△ABC的斜边AB上的中线,
∴CD=AD=BDAB=5,S△ACD=S△BCDS△ABC=12,
作AH⊥CD于点H,则∠AHC=90°,
∵S△ACD5AH=12,
∴AH,
∴CH,
∵CE,
∴EH=CH﹣CE,
∴AE,
故答案为:.
14.解:如图,
由题意得:∠CAD=90°,CD2=25,CD2=169,
∴AD2=CD2﹣AC2=144,
∴AD=12或﹣12(不合题意,舍去),
∴字母B所代表的正方形的边长为12,
故答案为:12.
15.解:方法一:过点Q作QH⊥AB于点H,在HA上截取HD=HB,连接QD,如图所示:
∴QH是线段BD的垂直平分线,
∴QD=QB,
在△ABC中,∠C=90°,AC=BC,
∵∠CAB=∠CBA=45°,
∴∠CAE=30°,∠CBF=15°,
∴∠QAB=∠CAB﹣∠CAE=15°,∠QBA=∠CBA﹣∠CBF=30°,
在Rt△BQH中,∠QBA=30°,QB,
∴QHBQ,
由勾股定理得:BH,
∴HD=HB,
∴DB=DH+HB=3,
∵QD=QB,
∴∠QDB=∠QBA=30°,
∵∠QDB是△DAQ的外角,
∴∠QDB=∠QAB+∠DQA,
∴∠DQA=∠QDB﹣∠QAB=30°﹣15°=15°,
∴∠DQA=∠QAB=15°,
∴AD=QD,
∴AB=AD+DB=3,
∴ACAB=3,
方法二:过B作BM⊥AE交直线AE于M,连接CM,
∵∠C=90°,AC=BC,
∴∠CAB=∠CBA=45°,
∵∠CAE=30°,
∴∠AEB=∠CAE+∠C=120°,
∴∠AEC=∠BEM=60°,
∵∠CBF=15°,
∴∠BQE=180°﹣∠AEB﹣∠CBF=45°,
∵BM⊥AE,
∴∠BMQ=90°,∠BQM=∠QBM=45°,
∴QM=BM,,
∴,
∴∠EBM=90°﹣∠BEM=30°,
∴BE=2EM,
∵BE2=EM2+BM2,
∴,
解得BE=2(负值已舍去),
∴CE=BC﹣BE=AC﹣2,
∵∠CAE=30°,
∴AE=2CE,
Rt△ACE中,AE2=AC2+CE2,
∴(2CE)2=CE+AC2,
解得(负值已舍去),
∴,
解得;
故答案为:3.
三.解答题(共8小题,满分75分)
16.解:(1)△DEF是直角三角形,理由如下:
由勾股定理得:AB2=22+12=5,BC2=52+32=34,AC2=62+12=37,DE2=32+12=10,EF2=62+22=40,DF2=72+12=50,
∵5+34=39≠37,
∴AB2+BC2≠AC2,
∴△ABC不是直角三角形,
∵10+40=50,
∴DE2+EF2=DF2,
∴△DEF是直角三角形;
(2)设△DEF中DF边上的高的长为h,
∵S△DEFDE EFDF h,
∴DE2 EF2=DF2 h2,
∴h28,
∴h2,
答:△DEF中DF边上的高的长为2.
17.(1)证明:∵△ABC中∠B=30°,∠ACB=90°,
∴∠BAC=90°﹣30°=60°,
根据题意可得:DE垂直平分AB,
∴B D=A D,A C=18,B C=12,
∴∠DAB=∠B=30°,
∴∠DAC=60°﹣30°=30°,
∴AD平分∠BAC,
∵DE⊥AB,DC⊥AC,
∴CD=ED.
(2)解:根据解析(1)可知,AD=BD,
设CD=x cm,则AD=BD=(8﹣x)cm,
∵在Rt△ACD中,AD2=CD2+AC2,
则(8﹣x)2=x2+62,
解得:,
即CD的长为.
18.解:(1)如图2,过点C作CF⊥DE于点F,
∵∠CDE=45°,
∴△CFD是等腰直角三角形,
∴CF=DF,
在Rt△CFD中,由勾股定理得:CF2+DF2=CD2,
∴2CF2=CD2=162,
∴CF=8(cm)(负值已舍去);
(2)如图3,过点C作CH⊥DE于点H,
∵将CD绕点D逆时针旋转15°后,点B恰好落在直线DE上,
∴∠CDE=45°﹣15°=30°,
∴CHCD16=8(cm),
∴端点C到底座DE的距离减少了(88)cm.
19.(1)证明:连接AE、CE,
∵∠BAD=90°,E为BD中点,
∴AEDB,
∵∠DCB=90°,
∴CEDB,
∴AE=CE,
∵F是AC中点,
∴EF⊥AC;
(2)解:∵AC=8,BD=10,E、F分别是边AC、BD的中点,
∴AE=CE=5,CF=4,
∵EF⊥AC.
∴EF3.
20.解:(1)∵∠BAC=120°,AB=AC,
∴∠B=∠ACB=30°,
由旋转的性质得:AD=AE,∠DAE=120°,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE=30°,
∴∠BCE=∠ACB+∠ACE=30°+30°=60°,
故答案为:BD=EC,60°,
(2)(1)中的结论成立,证明如下:
∵∠BAC=120°,AB=AC,
∴∠B=∠ACB=30°,
由旋转的性质得:AD=AE,∠DAE=120°,
∴∠AED=∠ADE=30°,∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴BD=EC,∠ADB=∠AEC,
∵∠ADB+∠ADF=180°,
∴∠AEC+∠ADF=180°,
即∠DEF+∠AED+∠ADE+∠EDF=180°,
∴∠DEF+∠EDF=180°﹣30°﹣30°=120°,
∴∠F=180°﹣(∠DEF+∠EDF)=180°﹣120°=60°;
(3)如图2,过点E作EG⊥DF于点G,
则∠EGF=∠EGD=90°,
由(2)可知,△ABD≌△ACE,∠F=60°,
∴S△ABD=S△ACE,∠EGF=90°﹣∠F=30°,
∴S四边形ABFC=S四边形ADFE,GFEF42,
∴EG6,DG=DF﹣GF=8+228,
∴DE10,
过点A作AH⊥DE于点H,
则DH=EHDE=5,∠AHD=90°,
∵∠ADE=30°,
∴AD=2AH,
∴DHAH=5,
∴AH,
∴S四边形ABFC=S四边形ADFE=S△ADE+S△DEFDE AHDF EG10(8+2)×624+624.
21.解:(1)∵AB∥CD,
∴∠EGC=∠BEG,
∵GF平分∠EGC,EF平分∠AEG,
∴∠FEG+∠FGE∠AEG∠EGC(∠AEG+BEG)90°,
∴∠EFG=180°﹣(∠FEG+∠FGE)=180°﹣90°=90°;
(2)由(1)知∠P=90°,
即△ABP是直角三角形,
∴S△ABP618(m2)
∴点P到AB距离为:182÷12=3(m),
∵AD的长度是点P到AB距离的倍,
∴AD=39(m),
∴S梯形ABCD(AD+BC)×CD(6+12)×654(m2),
∴健身区的面积为541836(m2),
答:健身区的面积为36m2.
22.解:(1)∵DE垂直平分AB,
∴DA=DB,
∴∠A=∠DBA=38°;
∵∠C=90°,
∴∠CBD=180°﹣90°﹣76°=14°.
故答案为:14°;
(2)设DA=DB=λ,则DC=6﹣λ;
由勾股定理得:λ2=(6﹣λ)2+42,
解得:λ,
即AD的长为.
(3)∵△ABC的面积为2m+4,
∴AC BC=2(2m+4);
∵AB=m,
∴AC2+BC2=m2,
∴(AC+BC)2=AC2+BC2+2AC BC=m2+4(2m+4)=(m+4)2,
∴AC+BC=m+4(负值已舍去),
∴△BCD的周长=CD+BD+BC=AC+BC=m+4.
23.解:(1)由知,这是利用勾股定理的逆定理,即依据1是勾股定理是逆定理;依据2是数形结合思想的运用;
故答案为:B;C;
(2)补全图形如下:
(3)
=8﹣1﹣2﹣2=3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
